AD-rfMRI图像的基于改进EDC的独立分量数目估计
郑伟,王轩,姚纪智,刘帅奇,张晓丹,马泽鹏
(1.河北大学 电子信息工程学院,河北 保定 071002;2.河北省数字医疗工程重点实验室, 河北 保定 071002; 3.河北省机器视觉工程技术研究中心, 河北 保定 071002;4.河北大学附属医院CT-MRI诊断科, 河北 保定 071000)
功能性磁共振成像(functional magnetic resonance imaging,fMRI)和弥散张量成像等成像方式作为一种应用于活体的、非侵入式、无损伤的功能成像方式,时间和空间分辨率相对较高,是目前实现阿尔茨海默病(AD)早期诊断的重要成像方式[1-2]. 而基于fMRI的功能连接可以反映脑区之间是否相关以及相关性的大小,从而反映AD患者早期及病程发展过程中脑区之间相关性的变化规律,因此具有更好的研究前景.静息态功能磁共振成像(resting state fMRI,rfMRI)不需要额外刺激,干扰因素较少,操作简单而且容易实现,可重复性较高. 2017年,Zhang等[1]扫描了96名受试者的rfMRI图像,采用独立分量分析将丘脑分成10个独立分量后,通过聚类将独立分量划分成不同的功能簇,每个簇对应唯一的一个时间序列,通过计算簇时间序列之间的相关系数研究丘脑的功能连接性,结果表明,独立分量分析与聚类结合对脑区的功能连接分析优于基于种子区的分析方法. 2018年,刘怡秋等[3]将半高全宽值为6 mm的高斯核用于对AD患者的rfMRI图像进行空间平滑,计算自动解剖标签模板(AAL)中116个脑区时间序列之间的相关性,并通过单因素方差分析,伪发现率(false discovery rate,FDR)校正以及双样本t检验比较AD病程发展过程中受试者的功能连接变化. 郑伟等[4]等针对不同年龄段女性患者静息态功能磁共振成像,采用独立分量分析及聚类等方法进行盲源分离和稳定性分析,通过统计检验及组间对比研究女性患者各脑区之间的连接关系及其强弱,进而判断功能连接差异,为女性AD患者临床前期诊断提供参考. 2019年,马文洁等[5]对rfMRI图像进行时间层校正、头动校正、空间归一化以及去线性趋势、滤波后,基于种子点选择默认模式网络与背侧注意网络,并将相关系数用于计算功能网络时间序列之间的相关性,从而研究AD患者感兴趣区域的功能连接异常,为探寻AD的发病机制和发病规律提供支持. 基于负熵的快速独立分量分析(fast independent component analysis algorithm based on negative entropy,NE-FastICA)算法收敛速度快,分离精度高,在脑功能连接分析中普遍使用, 但存在分离之前独立分量数目的过估计问题. 本文提出对实现独立分量数目估计的有效检测准则(effective detection criteria,EDC)进行改进,将对数函数用于惩罚函数,并与黄金分割法确定参数γ相结合,本文称其为OIEDC2,改进后解决了分量数目的过估计问题,给出了合理的估计数目.
1 受试者fMRI分组情况
本文将65~80岁的89名女性AD患者的rfMRI图像(来源于ADNI数据库https://ida.loni.usc.edu/login.jsp?project=ADNI)作为研究对象,按照疾病的发展阶段分为4组,对照组受试者(subjects of normal control,fsub_CN)17人、早期轻度认知障碍受试者(subjects of early mild cognitive impairment,fsub_EMCI)23人、晚期轻度认知障碍受试者(subjects of late mild cognitive impairment,fsub_LMCI)19人和AD受试者(subjects of AD,fsub_AD)30人的rfMRI图像,受试者情况如表1所示. rfMRI的相关参数如表2所示.

表1 受试者基本信息

表2 图像基本参数
2 基于EDC的独立分量数目估计
基于信息理论准则的估计方法主要包括贝叶斯信息准则(bayesian information criterion,BIC)[6]、赤池信息准则(akaike’s information criterion,AIC)[7]、最小描述长度(minimum description length,MDL)[8]、kullback-leibler信息论准则(kullback-leibler information criterion,KIC)[9]和EDC[10],这些信息理论准则通过最小化目标函数实现对独立分量数目的自适应估计,EDC估计如式(1)所示.
(1)
其中,-2L(x(n)|θk)可衡量EDC模型对数据的拟合程度,η(θk,N)CN为惩罚函数项,γ∈[0.1,1]为调整惩罚项的参数,可以调整估计性能,惩罚项中CN是可变的.2种不同惩罚函数下的EDC分别用EDC1和EDC2表示,如式(2)和式(3)所示.
EDC1(k)=-2L(x(n)|θk)+η(θk,N)(NlgN)γ,γ∈[0.1,1]
,
(2)
EDC2(k)=-2L(x(n)|θk)+η(θk,N)Nγ,γ∈[0.1,1]
.
(3)
信息理论准则用于估计独立分量数目时,若对rfMRI估计的独立分量数目在20~40,表明估计结果较合理[10]. 将AIC、KIC、BIC、MDL、EDC1以及EDC2用于估计4组受试者的独立分量数目,结果如图1所示.
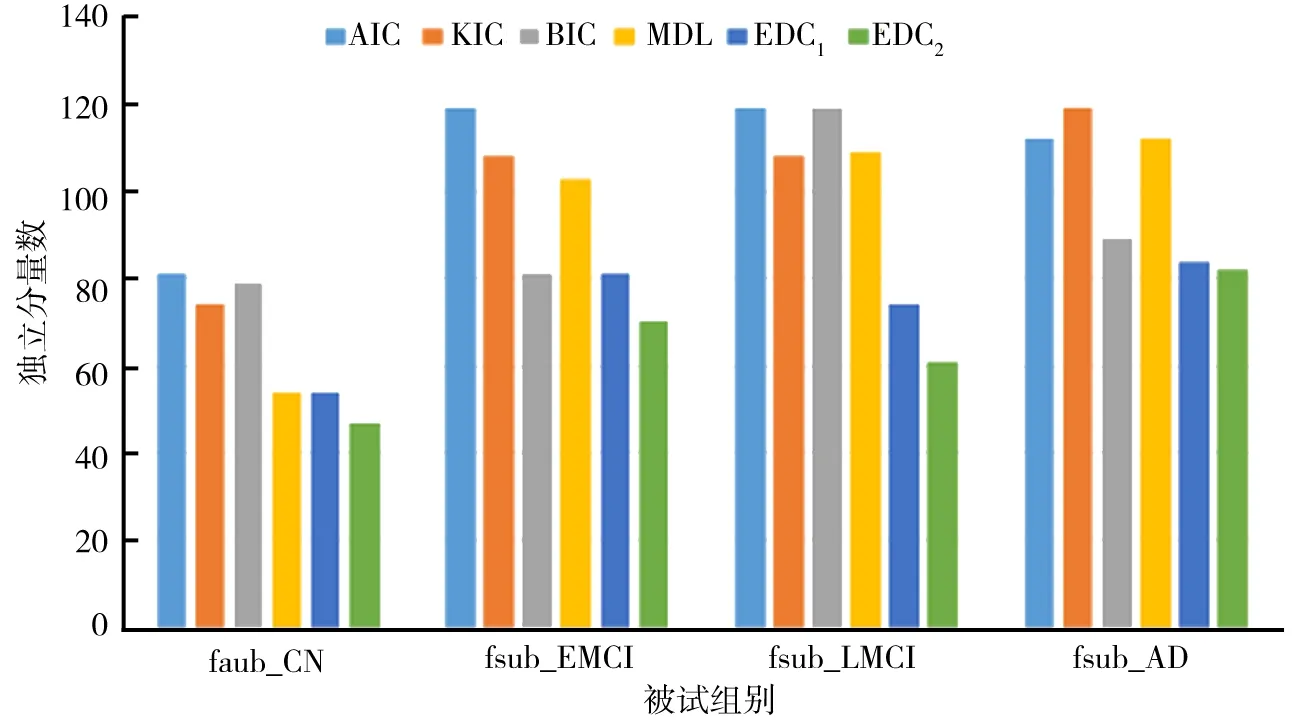
图1 不同准则下对4组受试者的估计结果对比Fig.1 Comparison of estimation results of four groups of subjects based on different criterion
由图1可知,AIC、KIC、BIC和MDL的估计性能接近,且在fsub_EMCI、fsub_LMCI和fsub_AD中均存在严重的过估计问题;EDC1和EDC2对每组受试者估计的独立分量数目相对较少,虽然EDC2存在过估计问题,但估计性能优于EDC1.
EDC2的过估计问题是由于其惩罚函数和γ值的非最优性导致的,本文提出将对数函数引入惩罚函数,并结合黄金分割法确定γ最优值的EDC2改进策略.
3 改进惩罚函数的EDC2及实验对比分析
3.1 基于对数惩罚函数的改进EDC2
式(1)中的惩罚函数项η(θk,N)CN的CN项是可变的,满足式(4)所示的条件.
(4)
其中,N为rfMRI的混合信号数,即体素数.
由式(3)可知,EDC2中CN=Nγ对γ求一阶导数的结果如式(5)所示.
CN=NγlnN,γ∈[0.1,1]
,
(5)
其中,N较大时,随着γ值增大,CN的变化率较快,EDC2估计的独立分量数减小的较快,容易造成低估计;γ值减小时,EDC2估计的独立分量数增加的较快,容易造成过估计.
由于对数函数在自变量较大时变化趋势较为平缓,本文将对数函数引入惩罚函数项,用于改进EDC2,称为改进有效检测准则(improvement of effective detection criteria,IEDC2),如式(6)所示.
CIEDC2=[loga(N)]γ,γ∈[0.1,1]
,
(6)
其中,a为对数函数的底数,可以取2、e和10.
改进的惩罚函数项需满足式(4),下面将给出证明:
首先计算关于式(6)的2个极限,CIEDC2与N比值的极限如式(7)所示.
(7)
函数y=loga(N)是一个单调递增函数,相同N下,γ=1时CIEDC2达到最大值,由于N→∞时,N达到∞的速度比loga(N)快,式(7)中CIEDC2取最大值时的极限为
(8)
当γ=0.1时CIEDC2达到最小值,N→∞时,N达到∞的速度比[loga(N)]0.1快,式(7)中CIEDC2取最小值时的极限如式(9)所示.
(9)
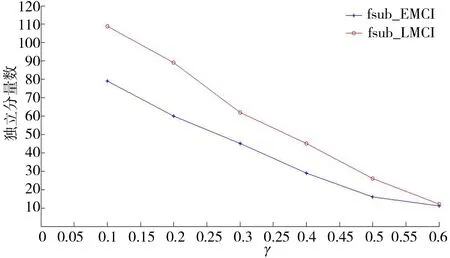
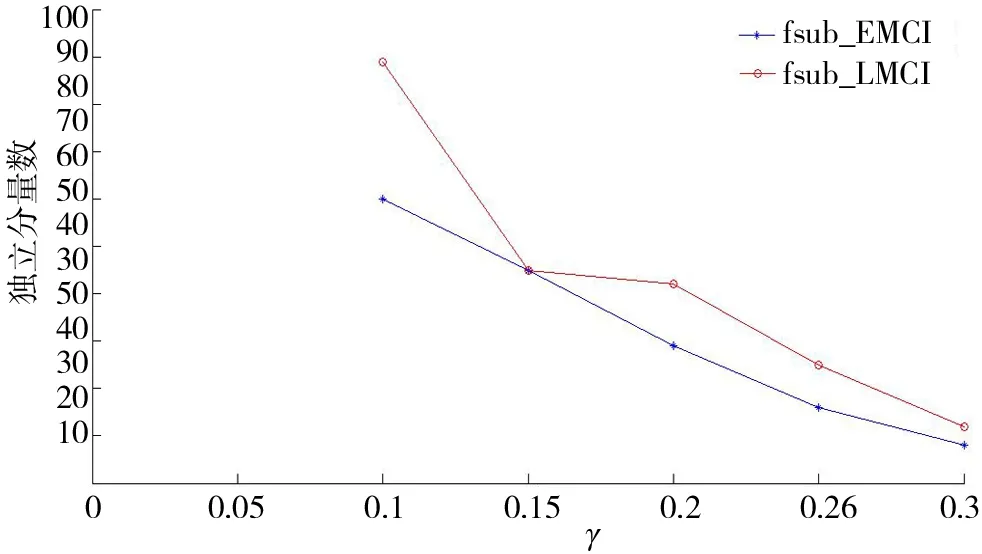
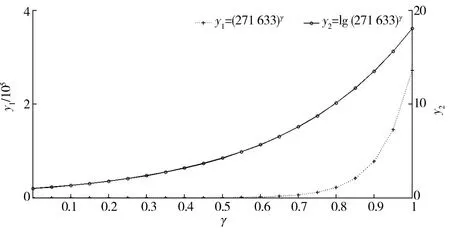
CIEDC2与CIEDC2max、CIEDC2min之间满足CIEDC2min (10) CIEDC2与lglgN比值的极限如式(11)所示. (11) 对数函数换底公式如式(12)所示. (12) 将式(12)代入式(11),结果如式(13)所示. (13) 若令lgN=u,则式(13)可转化为式(14). (14) 其中(lga)γ为与u无关的常数,则式(14)可写成式(15). (15) 当u→∞时,指数函数达到∞的速度比对数函数快,因此式(11)的推导结果为 (16) 由式(10)、式(16)可知,式(6)作为惩罚函数时满足式(4)的条件,因此将对数函数引入EDC2以改进惩罚函数项,是合理的. 式(6)中,底数a不同时,对数函数变化趋势不同,a取2时记为f1=log2x,a取e时记为f2=lnx,a取10时记为f3=lgx,3种常用对数函数变化趋势对比如图2所示. 图2 3种函数变化趋势对比Fig.2 Comparison of three logarithmic functions 由图2可知,底数越大,函数值越小,3个函数中f3的值最小,反映为自变量较大时f3的变化趋势较平稳,本文将f3用于IEDC2惩罚函数得式(17),则IEDC2估计可表示为式(18). CIEDC2=η(θk,N)(lgN),γ∈[0.1,1]. (17) IEDC2(k)=-2L(x(n)|θk)+η(θk,N)(lgN),γ∈[0.1,1] . (18) 为了衡量IEDC2改进后的估计性能,以fsub_EMCI、fsub_LMCI 2组受试者为例,将EDC2、IEDC2在不同γ值下的估计结果进行对比. EDC2的估计结果如图3a所示,图3a中EDC2对2组受试者的估计结果存在过估计问题;γ值越小,估计的独立分量数目越多,γ值越大,估计的独立分量数目越少,不同γ参数下,EDC2对fsub_EMCI估计的独立分量数目有3个值为20~40,对fsub_LMCI估计的独立分量数目有4个值为20~40,选择的独立分量数目不同会导致盲源分离结果也不同. IEDC2的估计结果如图3b所示,2组受试者的估计结果虽然在参数γ较小时仍存在过估计问题,但与图3(a)相比,相同γ值下,IEDC2估计的独立分量数目明显下降,表明IEDC2改善了过估计问题;不同参数γ下,IEDC2对fsub_EMCI、fsub_LMCI估计的独立分量数目均只有1个值在20~40,表明IEDC2避免了因独立分量数目不同导致的盲源分离结果出现差异,提高了估计结果准确性. a.EDC2;b.IEDC2. EDC2的估计性能除了受到不同惩罚函数的影响外,还与参数γ有关,γ越大EDC2估计的独立分量数越少,越容易造成低估计;γ越小,EDC2估计的独立分量数越多,越容易造成过估计. 将EDC2中的CN记为y1=Nγ=271 633γ,IEDC2中的CN记为y2=[lg(271 633)]γ,则y1、y2随γ值变化的趋势如图4所示. 图4 y1和y2随γ值的变化趋势对比Fig.4 Comparison of the change trend of y1 and y2 with γ values 图4中横轴为参数γ,左边纵轴对应y1=271 633γ的函数值,右边纵轴对应y2=[lg(271 633)]γ的函数值,对比可知,体素数N一定时,相同γ值下,y1函数值的变化率快,表现为γ值增加时,EDC2估计的独立分量数减小较快,容易造成低估计;γ值减小时,EDC2估计的独立分量数增加较快,容易造成过估计. 本文针对不同γ值下EDC2对4组受试者的估计结果存在过估计问题提出改进,在IEDC2惩罚函数的基础上,利用黄金分割法确定γ的最优值,改善IEDC2的估计性能.将黄金分割法用于确定最优γ值优化改进有效检测准则,本文简称为OIEDC2. 黄金分割法每次将搜索区间缩小0.618倍,根据精度要求以0.618n的缩减速率寻找最优点.γ值的范围是确定的记为[a,b],黄金分割法首先确定2个初始实验点r1和r2,其中实验点r1由式(19)确定.实验点r2由式(20)确定. r1=a+0.618×(b-a). (19) r2=a+b-r1=b-0.618×(b-a) . (20) 黄金分割法第一次确定2个实验点,之后通过对比、迭代依次确定下一个实验点,同时更新变量区间,缩小变量范围,最终通过评价函数确定最优点.黄金分割法通过不断更新γ的区间最终确定参数γ的最优值,直至IEDC2(γ)满足式(21).将满足式(21)的γ称为参数γ的最优值,记为γbest.将γbest用于式(18)可得OIEDC2估计如式(22)所示. 20≤IEDC2(γ)≤40 . (21) OIEDC2(k)=2L(x(n)|θk)+η(ηk,N)[lgN]γbest. (22) 为了衡量OIEDC2改进后的估计性能,将EDC2、IEDC2和OIEDC2分别用于估计4组受试者的独立分量数目,结果如表3所示. 表3 EDC2、IEDC2和OIEDC2的估计结果 由表3可知,EDC2对4组受试者的估计结果均存在不同程度的过估计问题;IEDC2对fsub_CN估计的独立分量数在20~40,估计结果较合理,对其余3组受试者虽然存在不同程度的过估计问题,但对fsub_LMCI估计的独立分量数与40较接近,估计结果比EDC2好,对fsub_EMCI和fsub_AD估计的独立分量数比EDC2低,表明与EDC2相比,IEDC2的估计性能有所改善;OIEDC2对4组受试者估计的独立分量数目均处于20~40,估计结果都比较合理,因此本文改进后的OIEDC2避免了过估计问题,实验结果比改进前的EDC2要好. 本文对基于EDC2的独立分量数目估计方法进行改进.将对数函数引入EDC2的惩罚函数项,称为IEDC2,将黄金分割法引入IEDC2确定最优参数γ,称为OIEDC2,并将结果进行对比分析,衡量EDC2改进前后的估计性能.实验结果表明,本文方法有效解决了4组受试者独立分量数目的过估计问题,估计结果更合理.为后续的基于独立分量的盲源分离,独立分量选择,感兴趣区域功能连接计算,实现4组受试者的功能连接分析,并通过统计检验获取随疾病发展进程感兴趣区域功能连接的变化规律,进而为寻找导致功能连接变化的内外部因素以及性别与AD发病的关系,即为AD发病机制的研究奠定基础.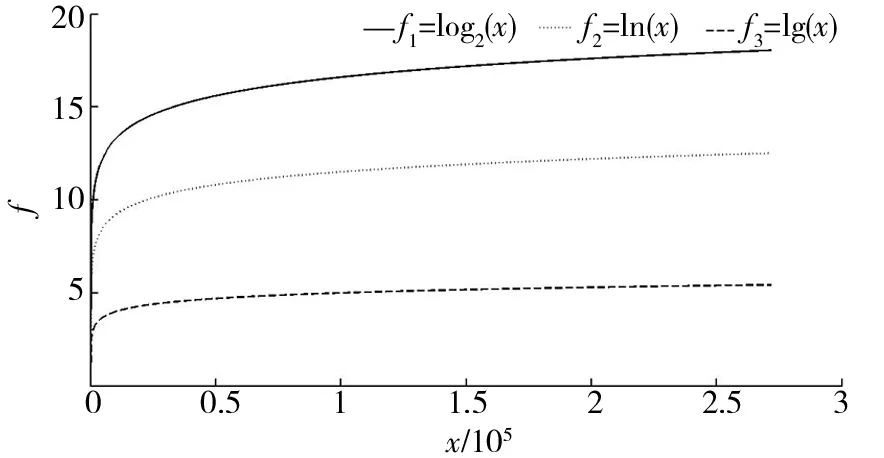
3.2 IEDC2实验结果及对比分析
4 基于黄金分割法的γ值确定
5 实验结果及对比分析

6 结论

