如何正确运用t检验
——两算术均值比较一般差异性t检验及SAS实现
张洪璐 ,刘媛媛 ,李长平 ,2,胡良平
(1.天津医科大学公共卫生学院,天津 300070;2.世界中医药学会联合会临床科研统计学专业委员会,北京 100029;3.军事科学院研究生院,北京 100850
t分布的发现使得小样本统计推断成为可能,以t分布为基础的检验称为t检验[1]。在医学统计学中,t检验具有所需样本量小、计算简便及检验效能较高等特点,成为应用较多的一类假设检验方法[2]。若统计分析的目的是比较算术均数,根据试验设计类型,t检验可以分为三种:单组设计一元定量资料t检验、配对设计一元定量资料t检验和成组设计一元定量资料t检验[3]。基于算术均数的t检验的应用条件一般包括:随机样本(即独立性)、来自正态分布总体(即正态性)以及两总体方差相等(即方差齐性)[4]。本文将分别介绍上述三种类型的一般差异性t检验,并结合实例,采用SAS 9.4予以实现。
1 基本概念
1.1 算术均数及其计算公式
算术均数是大家最为熟悉的平均数指标[5],是指一个变量所有观测值的总和除以观测值的个数,反映一个变量所有观测值的平均水平,简称为均数或均值。样本均数用表示,计算公式见式(1):

如果没有收集到个体观测值数据,而只是获得了汇总的频数分布表数据,则可用每个组段的组中值作为该组段中各个观测值的估计值,并用式(2)计算均数的近似值:

式(2)中,fi为第i组段的频数,xMi为对应组段的组中值,xMi=(第i组段上限+第i组段下限)/2。
均数计算简便,易于理解,是应用最为广泛的平均数指标。但是均数对于特大或特小的观测值十分敏感。对于偏态分布数据,均数也会偏向拖尾一侧,不能很好地反映全部观测值的平均水平。因此,均数主要适用于描述不含极端值的对称分布变量的平均水平,这时均数位于分布的中心位置。
2 t检验的基本原理
2.1 单组设计一元定量资料t检验的基本原理
单组设计一元定量资料t检验,实际上是推断该样本来自总体均数μ与某一已知总体均数μ(0常为理论值或标准值)有无差别。零假设H0:μ=μ0,备择假设H1:μ≠μ0;检验水准:α=0.05。
单组设计一元定量资料t检验的检验统计量为:

式(3)中,分子是样本均数与零假设中μ0的差距,分母是样本均数的标准误,t统计量实为用标准误来度量的样本均数与μ0的差距。这个差距小,将倾向于接受零假设;这个差距大,将倾向于拒绝零假设。数学家已证明:式(3)定义的检验统计量t是服从自由度为n-1的t分布的随机变量。故可以依据实际计算出来的t检验统计量的数值以及t分布,做出接受或拒绝零假设的决定[6]。
2.2 配对设计一元定量资料t检验
配对设计一元定量资料的分析着眼于每一对中两个观察值之差d,这些差值构成一组资料,用t检验推断差值的总体均数是否为“0”。检验假设为:
H0:μd=0,即差值的总体均数为0;H1:μd≠ 0,即差值的总体均数不为0;检验水准:α=0.05。
当H0成立时,检验统计量为:
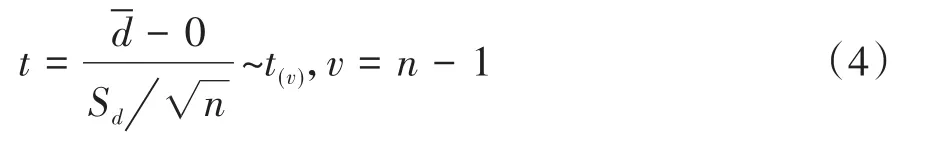
2.3 成组设计一元定量资料t检验
将受试对象随机分为两组,每一组接受一种处理(注意:对照组也可被视为一种处理)。一般把这样获得的两组定量资料视为代表两个总体的两个独立样本,据此推断它们的总体均数是否相等。此类检验也基于t分布,必需假定定量资料应满足独立性、正态性和方差齐性。
2.3.1 两样本所属总体方差相等,即具有方差齐性
检验统计量为:
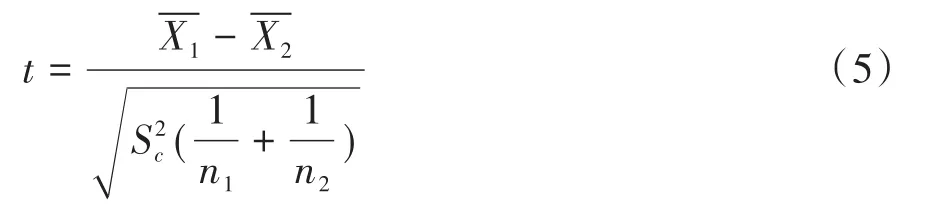

式(5)中的分子是两个样本均数之差,分母是样本均数之差的标准误,检验统计量t实为用标准误度量的均数之差。
可以证明,当H0成立时,这个检验统计量服从自由度为v=n1+n2-2的t分布。
根据式中算得检验统计量的数值后,利用这个t分布可得相应的P值。同样,依据实际计算出来的t检验统计量的数值以及t分布(自由度为n1+n2-2),给定一个小概率α作为检验水准,如果与t值相应的P值小于给定的α,拒绝H0;否则,不拒绝H0。
2.3.2 两样本所属总体方差不等
此时,可采用t'作为检验统计量:

式(6)中,分子仍是两样本均数之差,分母是均数之差的标准误,t'仍是用标准误度量的均数之差。
H0成立时,t'的分布比较复杂,可用如下自由度的t分布来近似t'的分布。

利用该式算得统计量t'的数值后,据此近似的t分布可以得到相应的P值。同样,给定一个小概率α作为检验水准,如果与t值相应的P值小于给定的α,拒绝H0;否则,不拒绝H0。
3 基于SAS的实例分析
3.1 单组设计一元定量资料t检验
【例1】大量研究显示,正常人的血清钙标准值是2.50 mmol/L,现有20名骨质疏松患者的血清钙测量值如下(单位:mmol/L):2.39、2.41、2.47、2.28、2.19、2.50、2.37、2.49、2.18、2.09、2.29、2.34、2.55、2.27、2.31、2.39、2.29、2.20、2.41、2.42。试比较骨质疏松患者血清钙与正常人是否不同。
SAS程序如下:

【程序说明】创建名为calcium的数据集,首先调用UNIVARIATE过程进行正态性检验,VAR语句后面的变量为待检验的血清钙测量值,然后调用TTEST过程,设置评价指标的理论均值h0为2.50。
【主要输出结果及解释】正态性检验的结果W=0.9785,P=0.9136,可以认为评价指标的测定值符合正态性的要求。t检验结果如下:t=-5.87,P<0.0001,骨质疏松患者血清钙均值与正常人不同,骨质疏松患者血清钙浓度均值2.34 mmol/L低于正常人血清钙浓度均值2.50 mmol/L。
3.2 配对设计一元定量资料t检验
【例2】采集10只正常成年大耳白兔下肢骨标本,共10对胫骨,行三点弯力学测试。从实验兔胫骨三点弯载荷挠度曲线得最大挠度,见表1。试比较双侧胫骨最大挠度是否不同。表1资料对应的实验设计类型为自身配对设计。
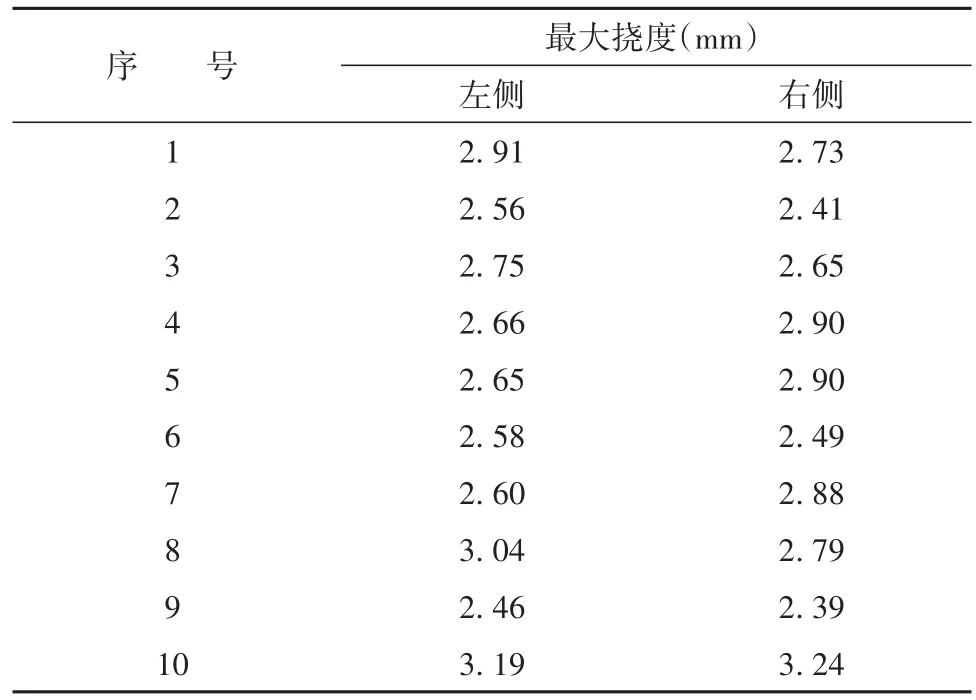
表1 10只家兔双侧胫骨最大挠度
SAS程序如下:

【程序说明】创建名为bending的数据集。首先生成一个新的变量d,代表每对中同一评价指标取值的差量;调用UNIVARIATE过程对其进行正态性检验;然后调用TTEST过程。与单组设计一元定量资料t检验的区别是,PAIRED语句后面为变量的对子,对子间用*连接。
【主要输出结果及解释】差值d正态性检验的结果为W=0.8808,P=0.1334,可以认为符合正态性的要求,t检验结果如下:t=0.03,df=9,P=0.9748,双侧胫骨最大挠度均值之间差异无统计学意义。
3.3 成组设计一元定量资料t检验
【例3】在一项氯氮平血浓度对白细胞总数的影响的研究中[7],研究者选取受试组28例,给予氯氮平治疗,对照组28例,比较受试组治疗一周末与三周末的血药浓度是否存在差异。假设测定的患者血药浓度(单位:μg/L)如下。治疗一周末血药浓度:49、417、229、342、445、700、273、50、286、212、516、444、334、176、170、434、791、219、384、213、96、327、217、16、256、438、102、495;治疗三周末血药浓度:1189、517、534、293、708、588、374、691、694、1025、278、611、854、597、721、479、530、755、610、583、672、71、194、457、132、570、721、421。试分析两组受试者血药浓度差异是否有统计学意义。
SAS程序如下:


【程序说明】创建名为blood的数据集,设置分组变量g,利用循环语句DO-END分别输入两组变量值。调用UNIVARIATE过程分别对两组定量数据进行正态性检验,CLASS语句后加分类变量。然后,调用TTEST过程,与前两种t检验的程序相比,增加了CLASS语句。
【主要输出结果及解释】两组定量资料均符合正态性的要求(一周末:W=0.9558,P=0.2757;三周末:W=0.9687,P=0.5463)。方差齐性检验的结果:F=1.75,P=0.1542,符合方差齐性的要求。t检验的结果见表2。t检验结果:t=-4.42,P<0.0001,两组血药浓度均值不同,治疗一周末血药浓度均值308.3 μg/L低于三周末血药浓度均值566.8 μg/L。

表2 成组设计一元定量资料t检验分析结果
4 讨论与小结
4.1 讨论
数据的集中位置表示大多数观测值所在的中心位置。算术均数是一个良好的描述集中位置的指标,具有计算简单、简明易解等优点。但每个数据或大或小的变化都会对均数造成影响。因此,均数更适用于描述呈正态分布数据的集中位置。在实际应用中,均数常和标准差相结合用于描述数据的集中趋势和离散程度。
t检验是在统计学中较常应用于定量资料差异性分析的一类假设检验方法。值得注意的是,对于定量资料而言,在数据分析时,应先考察该数据是否符合t检验的应用条件:①结合调查研究方式及样本来源等判断是否符合随机样本的要求;②调用UNIVARIATE过程进行正态性检验,若数据为非正态分布,则考虑采用变量变换的方式使其满足正态或采用非参数假设检验的方法;③在对成组设计一元定量资料进行分析时,对于正态分布的数据,要求其两总体方差相等,即满足方差齐性,若经检验方差不齐,则可使用t'检验。
此外,应根据专业知识确定选择单侧检验还是双侧检验。对于单因素k水平设计的定量资料或多因素设计的定量资料,应严格检查是否满足参数检验的前提条件,进而选择合适的检验方法[2]。
4.2 小结
本文基于3个实例,采用SAS软件实现了对单组设计、配对设计和成组设计下一元定量资料的t检验。在此过程中,借助直观判断法,考察了“独立性”的前提条件;借助UNIVARIATE过程中的选项“NORMAL”实现了正态性检验;借助TTEST过程中自身带有的方差齐性检验功能,实现了方差齐性检验。此外,还交代了基于均值比较的t检验的基本原理和应用时的注意事项。

