重心插值配点法求解Black-Scholes方程

赖舒琴 华之维 翁智峰

(华侨大学 数学科学学院，福建 泉州 362021)

0 引言

1973年，Black和Scholes[1]提出一种模型，称为Black-Scholes(B-S)模型，用于描述基础资产在期权定价中的近似行为.它已被期权交易员广泛使用，并因其在预测期权价格方面的有效性和准确性而导致期权交易的显著增长.直至今日，Black-Scholes方程仍是金融数学中期权定价理论的重要模型，研究其解有重要的现实意义.

目前，关于Black-Scholes方程的数值解法取得了很多进展.譬如，文献[2]给出Black-Scholes期权定价模型的二叉树方法、隐式差分方法和Crank-Nicolson差分方法等数值解法；文献[3]讨论了许多期权定价的数值计算问题及其现有数值方法的不足；文献[4]讨论了期权定价问题的鞅方法；文献[5]提出Black-Scholes方程的一种θ加权差分格式；文献[6]分析了美式期权定价的有限元方法；文献[7]利用代数变换消去方程中对空间的一阶导数项，导出四阶紧致差分格式；文献[8]用有限差分法研究一类带有参数α的广义Black-Scholes模型的数值解；文献[9]利用Laplace变换和有限差分方法来求解美式期权定价问题；文献[10]对支付红利下Black-Scholes方程构造了一种具有并行本性的交替分段Crank-Nicolson格式；文献[11]对欧式看跌期权定价问题构造一个四阶紧致有限差分格式.

最近，文献[12]利用重心插值配点法求解微分方程初边值问题，很多学者将该方法推广到求解各类微分方程，比如平面弹性问题[13]、分数阶Fredholm积分方程[14]和一维Allen-Cahn方程[15]等.重心插值配点法包括重心Lagrange插值和重心有理插值.对于给定插值节点，当选取Lagrange插值公式来构造近似函数时，由著名的Runge现象可以说明，当节点数量增大时，Lagrange插值公式构造的近似函数值容易出现Runge现象，具有极大的数值不稳定性.为了避免这一现象的出现，Berrut等[16]将Lagrange插值公式改进为重心型的Lagrange插值公式.由文献[17]可知，重心型的Lagrange插值公式克服了Lagrange插值的缺点，解决了震荡现象，具有了非常好的数值稳定性.此外，Berrut等[18]提出了一种简单的重心有理插值权，这之后Floater等[19]提出重心有理插值，其具有很好的节点适应性，有较高的精度，被称为一种理想的数值计算方法.重心插值配点法作为一种新型的无网格计算方法，其有效地避免了差分格式带来的累积误差，使用Chebyshev节点有效克服了Runge现象，且其具备计算格式简单、精度高、程序实施方便、节点适应性好等特点.如今，重心插值配点法广泛地被应用于弹性力学、微波技术及流体力学等多个方面[20.21].本文将该方法推广到求解Black-Scholes方程，时间和空间方向均采用重心插值Chebyshev配点法离散，以得到较高的数值精度，与前人工作比较，我们的算法在时间和空间方向上都具有高精度.

1 Black-Scholes方程的重心插值配点法

1.1 Black-Scholes方程的指数变换

考虑单个Black-Scholes方程的初边值问题

(1)

式中u为欧式看跌期权价格，u>0；S为股票价格，S>0；τ为时间；r为无风险利率，r>0；σ为股票价格S的波动率，σ>0；K为执行价格，K>0；T为到期日，T>0.

为便于用算例验证算法精度，令方程右端为f(x,t).此外，为消去(1)中偏导的变系数S，引入变换S=ex[7]，且作变换τ=T-t，将初始条件换为t=0时刻，则问题(1)化为

(2)

式中a,b是所取常数.

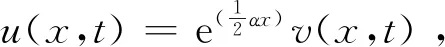
(3)

(4)

1.2 重心型插值

1.2.1 重心Lagrange插值. 设有n+1个不同节点xi(i=0,1,…,n)和对应一组值yi，p(x)为小于n次的多项式，满足p(xi)=yi(i=0,1,…,n)，这样的p(x)唯一存在，那么p(x)可写成Lagrange插值公式，即

(5)

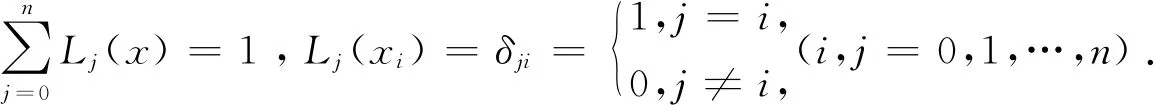
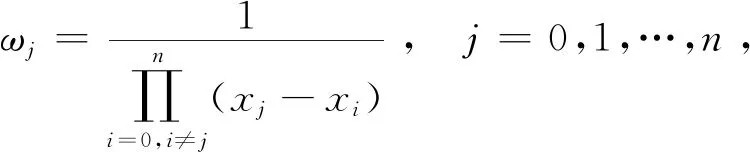
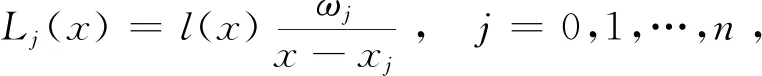
(6)

(7)

1.2.2 重心有理插值. 设有n+1个不同节点xi(i=0,1,…,n)以及对应的一组函数值yi，选择一整数d满足0≤d≤n，对每个j=0,1,…,n-d令pj(x)为d个点对(xj,yj),(xj+1,yj+1),…,(xj+d,yj+d)的次数至多为d的插值多项式，则令

(8)

容易证明式(8)的r(x)插值给定插值点对{(xi,yi),i=0,1,…,n}.于是，对于不同d(0≤d≤n)可得到一族有理函数插值，并且通过选择适当的参数d，可以提高插值精度.

此外，式(8)可写成重心插值形式，首先将pj(x)写成Lagrange插值形式，变形得

(9)

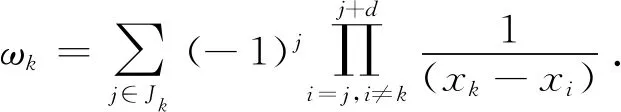
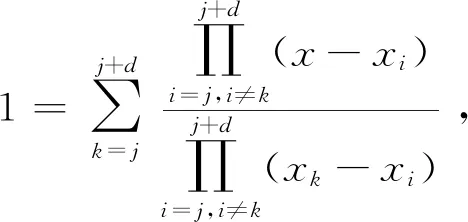
(10)

将式(9)和式(10)代入式(8)，得到高阶重心有理插值公式

(11)

1.3 重心插值配点法求解Black-Scholes方程

1.3.1 一维热传导方程的一般形式. 由于Black-Scholes方程经过指数变换转化为问题(4)，根据文献[23]的热传导方程，可知问题(4)与热传导方程类型相同，所以可考虑一维热传导方程的重心插值配点法.

以下为一般形式的一维热传导方程

(12)

边界条件为

v(a,t)=φ1(t),v(b,t)=φ2(t) 或vx(a,t)=φ1(t),vx(b,t)=φ2(t),

(13)

初始条件为

v(x,0)=ψ(x).

(14)

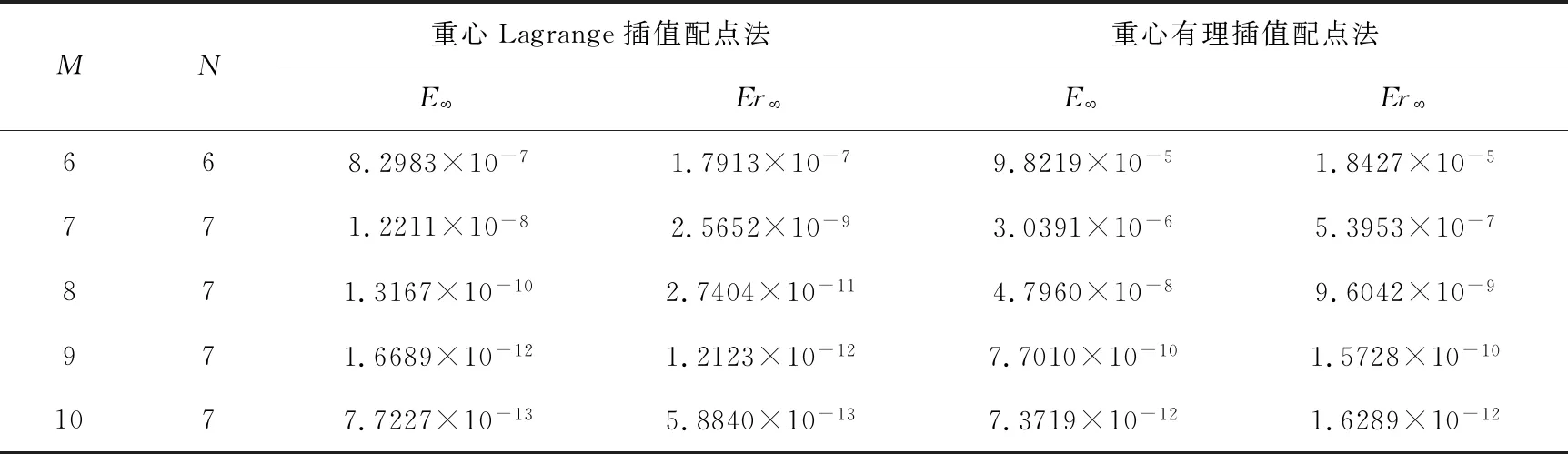
1.3.2 一维热传导方程的离散. 设时间域为[0,T]，将空间域[a,b]和[0,T]分别离散为m、n个第二类Chebyshev节点：a=x1

(15)

将式(15)代入方程(12)，且让方程(12)在点x1,x2,…,xm上成立，得常微分方程组，即

(16)

引进记号k(xi,t)=ki(t),g(xi,t)=gi(t),i=1,2,…,m，于是方程组(16)记为矩阵形式，即

(17)

将vi(t)在点t1,t2,…,tn的值vi(tj)=v(xi,tj):=vij，则vi(t)在t1,t2,…,tn上的重心插值函数为

(18)

将式(18)代入方程(17)，且让方程(17)在点t1,t2,…,tn上成立，得常微分方程组，即

(19)

(20)

式中符号⊗表示矩阵的Kronecker积：C(p),D(p)(p=1,2,…)分别为关于节点x1,x2,…,xm和节点t1,t2,…,tn的重心型插值p阶微分矩阵；Im、In分别为m、n阶单位矩阵.

[(Im⊗D(1))-k(C(2)⊗In)]V=G.

(21)

1.3.3 边界条件和初始条件的离散. 由于变换后问题(4)边界属于方程(13)前者这种形式，所以本文只作此边界的离散.

初始条件(14)的离散：v(xi,0)=vi1=ψ(xi),i=1,2,…,m，记作矩阵形式，即

1.3.4 Black-Scholes方程的重心插值配点格式. 依照一般形式一维热传导方程的重心插值配点法，可以推导出Black-Scholes方程变换后的问题(4)的重心插值配点法计算格式，即

[(Im⊗D(1))-λImn(C(2)⊗In)+βImn]V=G.

(22)

2 数值算例

2.1 算例1

考察如下微分方程初边值问题

(23)

右端项

下面分别利用重心Lagrange插值配点及重心有理插值配点进行计算，将两者进行比较.其中，空间方向采用Chebyshev节点数为m+1，时间方向采用Chebyshev节点数为n+1.

数值计算结果如表1所示，表中E=‖uc-ue‖表示误差的无穷范数，记作绝对误差，注：‖x‖表示相对误差的无穷范数，记作相对误差.

由表1知,在求解问题(23)时，随着节点数量增加，重心Lagrange插值配点法和重心有理插值配点法求解时的绝对误差E和相对误差Er均逐渐下降.此外，在节点数量相同时，利用重心Lagrange插值配点法求解方程时的E和Er均小于重心有理插值配点法的.

表1 不同插值配点法的计算结果

综上，重心Lagrange插值配点法和重心有理插值配点法对求解问题(23)都有较高精度.在节点数一样时，重心Lagrange插值配点法精度略高于重心有理插值配点法.由于重心有理插值中参数d使其精度具有不确定性，则重心Lagrange插值配点法的稳定性较高.

两种重心插值配点格式在区域x∈[0,1],t∈[0,1]的数值解及误差分布图，图1是数值解图，图2是误差分布图，其中符号x,t指问题(23)中变量，设数值解uc，误差error.

由图1中可知,重心Lagrange插值配点法和重心有理插值配点法求出的方程数值解图像均逼近于真实解，具有较高的精度.由图2可知,采用重心Lagrange插值配点法较重心有理插值配点法，有更高的精度.

2.2 算例2

考察问题

(24)

式中u为看跌期权价格；S为股票价格；τ为时间；r为无风险利率；σ为股票价格的波动率；K为执行价格；T为到期日.这里取S区间为[e-26,e4](对应的a=-26，b=4)，对空间、时间域各取81和41个计算节点，取r=0.005,σ=0.2,T=1,K=20.如图3所示，是方程(24)在重心Lagrange插值配点法下的数值解曲面.由图可知，用当前的计算格式可以得到光滑且稳定的数值解.

下面考察提出的计算格式(22)的运用有效性，采取以下方法,分别对问题(24)的参数σ,r,K,T取不同值，比较它们对欧式看跌期权的价格u造成的影响是否与实际情形一致.

结果如图4所示，由图4(a)可知，当取r=0.005,T=1,K=20，而σ在0.1、0.2、0.3、0.4中变化时，在股票价格S为执行价格20附近，股票价格的波动率σ升高会造成欧式看跌期权价格u的升高，这与金融界高风险、高回报的观点相符合.由图4(b)可知，当取σ=0.2,T=1,K=20，而r在0.005、0.05、0.1、0.15中变化时，发现当无风险利率r越高，欧式看跌期权价格u会下跌.由图4(c)可知，当取r=0.005,σ=0.2,T=1，而K在15、20、30、40中变化时，发现执行价格K的提高会引起欧式看跌期权价格u的提高.由图4(d)可知，当取r=0.005,σ=0.2,K=20，而T在0.5、1、1.5、2中变化时，发现欧式看跌期权价格变化不大.综上，以上结果均与实际情形一致，可证实计算格式(22)具备实用有效性.

3 结束语

本文针对单个的Black-Scholes方程，考察欧式看跌期权定价问题.首先利用指数变换消去Black-Scholes方程中的空间一阶导数，然后利用重心Lagrange插值配点法和重心有理插值配点法求Black-Scholes方程的数值解，并且通过数值算例一比较两种重心插值配点法的数值解精度.比较两种重心插值配点法，发现重心Lagrange插值配点法的精度略高于重心有理插值配点法.在第二个数值算例中，将重心Lagrange插值配点法运用到Black-Scholes方程的求解中，得知这种计算格式具备实用有效性.尤其与文献[11]的算法比较，我们的算法用很少的节点个数就使得时间和空间方向达到高精度.今后，可以将重心插值配点法推广到其他微分方程，也为今后解决同类问题提供一种很好的数值求解方案.