由一道余姚市教师大比武试题引发的思考
傅 绒 史日能
(1.浙江省余姚市梦麟中学 315400;2.浙江省余姚市第七中学 315400)
本人有幸参加了余姚市第二届青年教师大比武,该活动意在提高青年教师的教学能力,进一步推进师资队伍建设.无论是准备过程还是比赛过程都是一种自我的提高与成长,从中可以发现不足、查漏补缺,收获颇丰.比如在参加笔试时,第九道选择题就让我印象深刻.
一、问题的提出
第9道选择题是:函数y=f(x)在点x=x0处取得极大值,则必有( ).
A.f′(x0)=0 B.f″(x0)<0
C.f′(x0)=0且f″(x0)<0 D.f′(x0)=0或不存在
分析如果函数y=f(x)在x0可导,且在点x=x0处取得极大值,则必有f′(x0)=0;如果函数y=f(x)在x0不可导,但也有可能在点x=x0处取得极大值,例如函数y=f(x)=-|x|,由函数的图象可知在x=0处不可导,但有极大值.所以该题应选D.
疑惑:函数的二阶导数与函数的极值有什么关系呢?
二、问题的解决
人教版选修1-1里对函数极值的定义是:函数y=f(x)在点x=a的函数值f(a)比它在点x=a附近其它点的函数值都小,f′(a)=0;而且在点x=a附近的左侧f′(x)<0,右侧f′(x)>0.类似地,函数y=f(x)在点x=b的函数值f(b)比它在点x=b附近其它点的函数值都大,f′(b)=0;而且在点x=b附近的左侧f′(x)>0,右侧f′(x)<0.我们把点a叫做函数y=f(x)的极小值点,f(a)叫做函数y=f(x)的极小值;点b叫做函数y=f(x)的极大值点,f(b)叫做函数的极大值.极大值点、极小值点统称为极值点,极大值和极小值统称为极值.这是用函数的一阶导数来定义函数的极值,那么函数的二阶导数与它的极值又有什么关系呢?下面来研究它们的内在联系:
假设f″(x0)存在且不为0,x0是函数y=f(x)的极值点,则f′(x0)=0,由导数的定义可知:
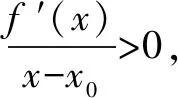
三、结论的得出
如果f″(x0)存在且不为0,x0是函数y=f(x)的极值点,若f″(x0)>0,则点x=x0是函数的极小值点,函数y=f(x)在x=x0处有极小值;若f″(x0)<0,则点x=x0是函数的极大值点,函数y=f(x)在x=x0处有极大值.
四、结论的应用
那么现在我们又多了一种求函数极值点的方法,下面我们用这种方法来解决一些常见的极值问题.
(1) 函数y=(x2-1)3+1的极值点是( ).
A.极大值点x=-1 B.极大值点x=0
C.极小值点x=0 D.极小值点x=1
解y′=3(x2-1)2·2x,令y′=0,得x=±1,0,y″=30x4-36x2+6.∵y″|x=-1=0,y″|x=1=0,y″|x=0=6>0,∴选C.




(3)2010年天津理科21题的第Ⅰ问是:已知函数f(x)=xe-x(x∈R),求函数f(x)的单调区间和极值.下面来解决这个函数的极值问题

显然用以上方法来求极值点与书本上提供的方法要来得简单方便,但是这种方法也不是万能的.对于某些复杂函数,如果出现f″(x0)=0的情况就不适用了,例如函数f(x)=x4(x-1)3.用函数的二阶导数来求极值点的方法适用于函数f″(x0)存在且不为0的时候.
通过对这道题目的思考使我对函数极值有了更深入与广泛的了解.正如克莱因所说的:“挑选好一个确定的研究对象,锲而不舍,你可能永远达不到终点,但是一路上准可以发现一些有趣的东西.”

