Skiptree：面向多维数据的可扩性范围查询的数据结构

叶培顺，史旭宁

(1.榆林学院 信息工程学院，陕西 榆林719000；2.铜川职业技术学院 继续教育学院，陕西 铜川 727031)

近几年来，基于集中式服务的网络结构逐渐向分布式结构和对等网络结构发展，这种结构就是可扩展的分布式数据结构(SDDS)，它首先是在LH*中提出的。建立在散列法或关键值匹配的基础上的新的分布式数据结构如Chord[1]，Viceroy[2]，Koorde[3]，Pastry[4]以及P-Grid[5]已经被提出，现在多数对等覆盖网为了达到路由O(logn)跳数，要求有O(logn)个链接每个节点，以DHTs为基础的Viceroy 和Koorde是很值得讨论的，因为仅有O(1)个链接的每个节点只能有O(n)跳数，如果要达到O(logn)跳数是以受约束或无负载平衡为代价的。

以DHTs和散列法为基础的系统无法进行范围查询，相反，那些基于关键值匹配的系统，尽管要求更复杂的负载平衡技术，却能支持范围查询。像P-Grid、 R-Tree和SkipNet[6]系统可以在单维空间中进行范围查询。为了在多维空间储存关键值，本文提出了一种新的可扩展的分布式数据结构叫Skiptree，该系统用一种分布式分割树把空间分成许多较小的区域，每个网络节点是这棵数的叶子节点，并且负责一个区域。为了便于与同样基于树的解决方法做比较，在这里分割树仅用来说明区域间的一种排序。路由机制和链接维护类似于SkipNet系统，并不依赖分割树的形状，所以通常情况下该系统不需要平衡这棵分割树。SkipNet系统是依靠叶子节点来维护，在这棵树里节点在跳跃中的顺序是与分割树的叶子从左到右定义的顺序相同。处理一个单个关键值查询与普通的SkipNet查询方法类似，而范围查询的不同主要归因于Skiptree本身的多维性时，从另一个角度来说，Skiptree可以看作是对SkipNet在多维空间的一种延伸。

1 Skiptree的基本结构

Skiptree由分割树组成，所有分割树的叶子形成了一个SkipNet系统。

假定每个数据单元有一个关键值，这个值是K维搜索空间中的一个点，当这个网络有N个叶子节点时，这个空间将被分成N个区域，也就是说每个叶子节点负责一个区域。图1就是一个描述两维空间的分割树的例子，分割树上的内部节点用数字表示，叶子节点用字母表示，每个叶子就代表一个区域。假设S(v)表示指向节点v的区域，其中v是对每个数据单元负责的节点，它的关键值在S(v)中。

图1 一棵两维树和它相应的空间分割

对于网络节点u，也就是分割树上叶子节点，我们把树的根部到节点u的路径叫做节点u的主要路径。这个路径上节点的超平面等式，我们把它认为是节点u特有的平面等式(Characteristic Plane Equations)，简称为u的CPE。在Skiptree中每个叶子节点储存它自己的CPE也储存它的那些链接的CPE。利用这些CPE的信息，在一个分割树上节点u左右两边或者是它的其它链接点的左右两边的点，每个节点跟u一样都能够在本地被识别。此后，我们提到一个平面，实质上就是指一个k维空间中k-1维的一个超级平面。

我们把在Skiptree中的网络节点如图2所示连在一起，按照前面所描述的，分割树中的叶子组成一个SkipNet。

图2 分割树中的叶子组成的SkipNet

2 查询处理

2.1单点查询

单点查询就是单个关键值查询，它的路由算法在本质上和SkipNet中的查询算法是相同的,就是每个节点沿着路径来接受查询,发送查询是通过最远的链接,如图3所示, 到达目标节点之间的长度是在每一个跃点都会被等分成2个节点,这就说明查询最多经过log2n跳后到达目标.然而，由于在网络中SkipNet是利用一种概率方法来选择和维护链接,所以它能保证路由在O(logn)跳数内。在文献[3]中给出了形式证明。

图3 单点查询

为确保节点上不同位置的点能顺序地在落在另一个节点包含的范围内，一个节点相对于CPE平面中不同位置的点就要能够显示从起始位置到根目录的主路径,直到它查询当前点落在第一个平面不同的位置的节点上,这个点包含在属于一个兄弟子树的一个区域中,如果子树是一个左(右)子树, 所有包含这个点的节点必须也是当前节点的左(右)节点。

2.2范围查询

Skiptree中范围查询是一个3元组即(R,fs,ls),其中R是多维空间的查询纬度, [fs,ls]是指所查询的区间，也就是说它查询这个序号仅仅是在[fs,ls]区间上的网络节点，一个正常的范围查询取值于(R，-∞，+∞)，因此所有的节点在忽略它们的序号的情况下，都会被查询到，注意R定义的区域可以是任意形状树，不管R与给定的超立方体是否相交,只要每个节点在本地能被识别。

当一个节点S接到一个范围查询(R,fs,ls)，只要那儿的节点在此链接和下个链接之间都与R区域相交，它就发送这个请求到它的每个链接，例如在图4中，假定A和B是S维护的两个连续链接相对应的两个节点，如果在与R相交的A和B之间有节点，那S向A发送一份搜索请求副本，每个这样的节点一定在图4中画阴影的子树中之一上。

事实上，这样的节点一定是标有“+”的右边节点和标有“-”的左边节点，因为S有与它链接相对应的所有的CPE，它也有权使用与标有“+”或“-”的内部节点相对应的平面等式。因此,它能容易地从介于A和B之间每一个子树相关联的多维空间领域内的等式内被识别, 并且从此它可以确定是否有一些介于A和B之间的子树的区域与R相交,以及是否有这样一个子树,它必须也包含一个区域与R相交的节点，注意一个查询的副本通过一个链接被发送出去之前要适当修正fs和ls 的查询区间，原因就是要约束被查询节点的顺序防止重复查询，例如在图4中，假如复制的三元组(R,fs,ls)从S发送到A，也可以假定A.seq 和 B.seq分别是A和B的序号，然后S计算这个区间[fs/, ls/]作为[fs,ls]和[A.seq, B.seq]的交集,向A发送(R,fs/,ls/)查询,这就确保了在这个网络中每个节点只接受一次查询。

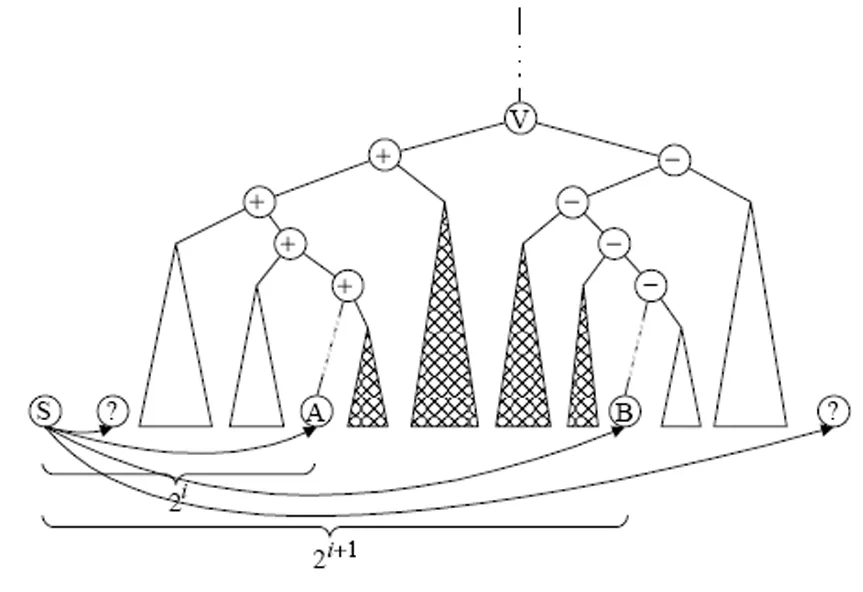
图4 一个范围请求是通过S维护的各个链接来传播

3节点的加入和离开

3.1节点的加入

为了加入到Skiptree中，一个新的节点v必须能够联系到现有的节点u。节点v首先插入到一个分割树中，这个分割树是用一个新的平面P把S(u)分成两个区域，一个区域分给v，而u保持支配其他区域,同样，v复制它的CPE从u和附加的平面P到双方的CPE。我们可以任意选择平面P，因为负载平衡协议将不断改变分割树来得到一个更平衡的结构。

分割树更新之后，v通过连接SkipNet建立了它自身的网络链接，这里节点序号是定义在这些节点中的一个全序号，仅仅只有O(logn)步。加入SkipNet的算法在文献[3]中被描述。

3.2节点的离开

和节点的加入类似，当节点v离开Skiptree时，它必须要经过以下三步。

第一步是更新这个分割树，假如在CPEv(节点v的CPE)中末尾的平面，我们把这个平面叫P，平面P 把它父亲区域分成S(v)和R两个区域，为了更新这个分割树，节点v对R中的节点发送一个专门的范围请求，通知它们把平面P从他们的CPE中移开，这样v从分割树中有效地移开。

第二步就是传送数据，对每个用单点请求的数据v能简单地发现这个节点并能正确地传送这个数据，然而，一个更有效的方法就是收集所有的可能的目标区域并在本地对这个请求进行评估。

最后一步，v必须从SkipNet中移开，在文献[3]中指出，这能被减少到使用类似于Chord和 Pastry的后台修正除去 O(1) 链接处理。

4总结

本文主要研究和论述了Skiptree这种数据结构在分布式环境下处理多维空间的单点查询和范围查询方法，详细论证了这种数据结构在每个节点上维护O(logn)个链接，并对单点查询保证一个最大值为O(logn)个信息，同时也保证深度为O(logn)的范围查询，研究具有一定的学术价值和意义。对于节点失败时的容错性和负载平衡以及存储最优化等问题还需进一步研究和讨论。