一种多普勒盲区下的航迹片段关联方法

韩 伟， 陈传生， 李志淮

(空军预警学院， 湖北武汉 430019)

0 引言

机载预警雷达采用下视探测方式，具有良好的低空探测性能，但由于采用脉冲多普勒体制，存在一定范围的多普勒盲区[1-3]，该盲区使得径向速度较小的目标无法被检测，从而造成目标点迹丢失和航迹中断。从信号处理层面，多普勒盲区难以消除，因此，可在数据处理层面，通过改进目标跟踪方法来减小多普勒盲区对目标航迹质量造成的影响。

一些学者针对多普勒盲区条件下的目标跟踪问题开展了深入研究，主要思想是将多普勒盲区先验信息并入到各种滤波算法中[4-6]。但以上研究均针对单目标环境，在实际探测过程中，存在杂波和多目标的情况，这就涉及到多目标数据关联的问题。

一些学者主要针对多目标数据关联方法进行了改进。一类是多普勒盲区下多目标概率密度类跟踪算法的改进[7-8]。一类是多普勒盲区下针对多维分配数据关联的改进[9-10]。但以上方法均是在滤波过程中完成目标点迹-航迹的关联，在多普勒盲区条件下，尤其是盲区范围较大时，无论采取何种先进的跟踪算法，航迹质量仍会不断降低，造成航迹中断。

与点迹-航迹关联的思想不同，Bar-Shalom等首次基于一种“后续”处理的航迹片段关联思想[11-12]，在航迹已经中断的条件下，采用基于二维全局最优分配的关联算法将属于同一目标的不同时段的航迹片段进行关联。国内一些学者针对导弹目标和飞机目标的航迹片段关联与优化问题进行了深入研究[13-17]，主要思想是将新、老航迹的关联问题等效为二维分配问题，分配的代价函数则利用了目标的运动状态信息的相似性。但以上研究均是在未知航迹中断原因的条件下开展的，未考虑多普勒盲区因素。因此，本文提出一种多普勒盲区条件下的基于二维分配的航迹片段关联方法，将多普勒盲区先验信息引入到二维分配的各个环节，最后再引入了其他传感器获取的目标识别信息，与目标运动信息共同组成二维分配代价函数，从而完成同一目标航迹片段的配对。

1 航迹片段关联的更新过程

在实际环境中，雷达的探测性能会受到多种因素的影响，目标航迹频繁连续丢点的现象时有发生。此时，不论采取何种跟踪方法，目标航迹仍可能发生中断。而当雷达重新获得目标的量测值时，根据航迹起始准则，新的航迹又会产生。这时，同一目标形成了多个不同航迹号的航迹片段，从而使得航迹质量严重下降，数据处理系统的负担也大大增加。因此需要采用一种基于航迹后期处理的航迹关联方法，将已发生中断的目标航迹片段进行关联和衔接，从而降低航迹片段数量，延长目标航迹寿命，从整体上改善航迹质量。

传统的多传感器航迹-航迹关联是将多个传感器获得的来自同一目标的航迹进行关联，与该关联类型不同，航迹片段关联是将同一目标在不同时间形成的航迹进行关联，这些航迹无时间交点，因此，需要首先对航迹进行预测和外推等预处理，使得这些航迹片段具有时间交点，然后利用多维信息构建航迹的关联度，采用相应的关联方法完成航迹片段关联。

航迹片段关联在两组航迹之间进行，这两组航迹定义如下：

1) 老航迹(用集合O表示)：由于缺少与之相关联的量测点迹，已确定为终结的航迹；

2) 新航迹(用集合y表示)：新起始的航迹(需要满足一定的长度)，它可能是某些中断航迹的延续，即新航迹和老航迹可能来源于同一目标。

图1表示了老航迹组O和新航迹组y的更新过程，主要包括以下三个过程：

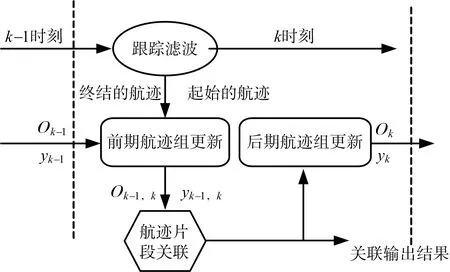
图1 航迹片段关联的更新过程

1) 前期更新：k时刻滤波后，如果终结的航迹和新起始的航迹出现，则将终结的航迹并入老航迹组Ok-1，新起始的航迹并入新航迹组yk-1，两个更新的航迹组分别用Ok-1,k和yk-1,k表示，两组航迹的数量可以不相等。

2) 航迹片段关联：两个航迹组Ok-1,k和yk-1,k被送到航迹片段关联模块完成多目标航迹关联。

3) 后期更新：关联的航迹对从两个航迹组Ok-1,k和yk-1,k中移除，得到新的航迹组Ok和yk。

2 航迹片段的二维分配

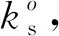
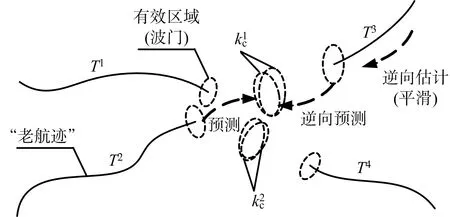
图2 航迹片段递推示意图

2.1 航迹片段预处理

1) 老航迹的预测

2) 新航迹的平滑

3) 新航迹的逆向预测

2.2 航迹片段初关联

在多目标密集杂波环境中，可能存在较多的空间位置相近的航迹片段，此时，为了减小关联范围，提高计算效率，首先进行航迹片段的初步关联。如图2所示，T1和T2分别为T3和T4的候选关联航迹，该候选航迹是根据初步关联产生的。这里，初关联主要利用目标的运动学信息，包括以下三个步骤：

1) 最大速度的限制

k时刻可能的老航迹和新航迹配对集合表示为

Φ={(Ti1,Tj1),…,(TiNk,TjMk)}

(1)

其中，老航迹为

(2)

新航迹为

(3)

Nk和Mk分别为k时刻老航迹和新航迹的数量。首先，设置速度门限。与点迹-航迹关联相同，速度门限取决于目标的最大速度。设置速度门限后，得到的候选航迹对集合可表示为

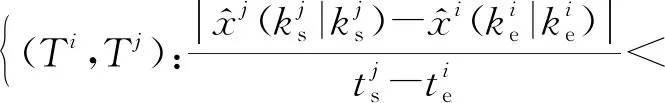
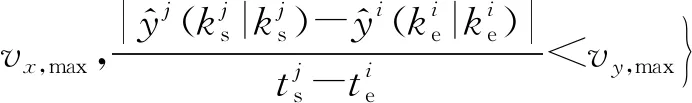
(4)

2) 径向速度的限制

(5)

其中，新老航迹估计径向速度之差为

(6)

相应的协方差

(7)

从而得到如下航迹配对集合

(8)

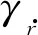
3) 距离的限制

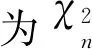
(9)

由于误差的独立性，其方差为

(10)

从而得到如下航迹配对集合

Φh={(Ti,Tj):(Δij)′[Pij]-1Δij≤γh,

(11)

式中，γh为门限值，可由真实量测落入波门内的概率PG获得。

2.3 二维全局最优分配

在完成了粗关联以后，得到了候选航迹对，然后对这些航迹进行全局的最优分配，其本质是一个二维分配问题。由于并非每条航迹都能与其他航迹关联，因此，在二维分配的每一列里增加一条空航迹，与空航迹关联的航迹片段表示虚警或新目标产生的航迹。故求解二维分配问题可以转化为求解以下的代价最小值：

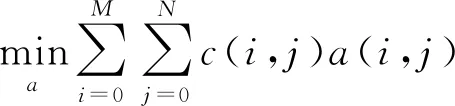
(12)

式中，M为老航迹片段的个数，N为新航迹片段的个数，i=0和j=0表示空航迹。式(12)满足以下限制条件：

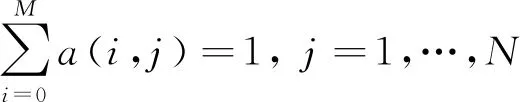
(13)

(14)

式(13)表示每条新航迹最多只能与一条老航迹关联，式(14)表示每条老航迹最多只能与一条新航迹关联。二进制分配变量a(i,j)可表示为

(15)

在高斯假设条件下，新老航迹相似量的似然函数可表示为

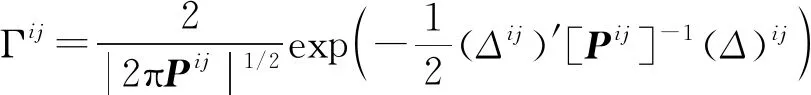
(16)

则分配代价c(i,j)可用负对数似然函数比表示为

(17)

式中，PDs为生成一条新目标航迹的概率。最后采用拍卖算法求取二维分配的最优解。

3 融合类别信息的航迹片段关联

3.1 目标类别信息

实际上，除了雷达获得目标的运动学信息(位置、速度)外，ESM、高分辨雷达等传感器还能获得目标的属性信息，如一维距离像、雷达脉内特征、目标运动包络等，该属性信息经过分类器可以用于目标分类，得到目标的类别信息[21]。加入目标类别信息后，雷达获得的量测值可表示为

Z(k)={z(k),ζ(k)}

(18)

式中，z(k)为目标的位置量测，ζ(k)为目标类别量测，即分类器的输出。假定有N类目标，且分类器的输出范围同目标类别范围的大小相同，则分类器的输出可表示为

ζ∈{1,…,N}

(19)

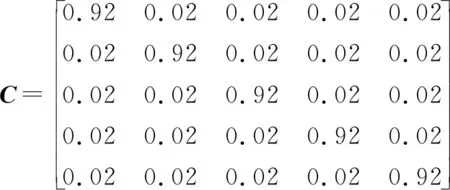
正如跟踪滤波器会有一定的跟踪误差，分类器也会存在目标类别判断的误差，其精度可以用“模糊矩阵”C=[cij]表示，C中的元素表示目标真实类别κ=i的条件下，分类器输出ζ=j的概率(ζ=j条件下的似然)，具体可表示为

cij=P{ζ=j|κ=i},i,j=1,…,N

(20)

因此，分类器输出为j时的类别概率向量是“模糊矩阵”C的第j列。在C的对角线元素已知的条件下，对角线以外的元素为(0,1)之间的值，C的每一行或每一列之和为1。

分类器的作用是计算目标类别的后验概率并进行目标类别的更新，在分类器输出ζ=j的条件下，目标类别κ=i的后验概率可表示为

(21)

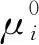
(22)

式中，cj为C的第j列向量，⊗为Schur-Hadamard积，ζk-1表示k-1时刻的累积分类信息，μ(0)=μ0。对于一条航迹而言，其类别概率向量可表示为

(23)

式中，μn(k-1)为k-1时刻更新的航迹的类别概率向量。

3.2 引入类别信息的航迹片段关联

1) 初关联

根据式(23)计算出所有老航迹和新航迹对应的目标类别，然后在式(11)的初关联基础上，将属于同一类别的航迹作为候选的航迹集合，这里将所有航迹片段最后时刻的类别概率向量的最大值作为目标的类别。

2) 类别代价函数

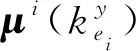
(24)

因此，新的代价函数可表示为

(25)

4 仿真实验及结果分析

在评价航迹片段关联算法的性能时，本文采用如下评价指标：

1) 全航迹寿命(Total Track Life, TTL)

TTL为来自同一目标的航迹片段的长度和与目标寿命长度的比值。

2) 平均航迹寿命(Mean Track Life, MTL)

MTL为全航迹寿命与全航迹寿命中航迹片段数目的比值。

3) 航迹中断数(Track Breakages, TB)

此处的TB是针对每一个目标进行定义，即在若干次蒙特卡洛仿真条件下，一个目标没有进行正确关联的航迹片段数之和。除此以外，航迹片段还满足以下条件：雷达采样间隔T=10 s；每个航迹片段至少包括6个点迹；连续丢失12个点迹，则目标航迹撤销。

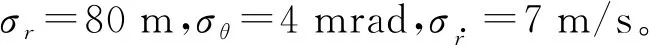
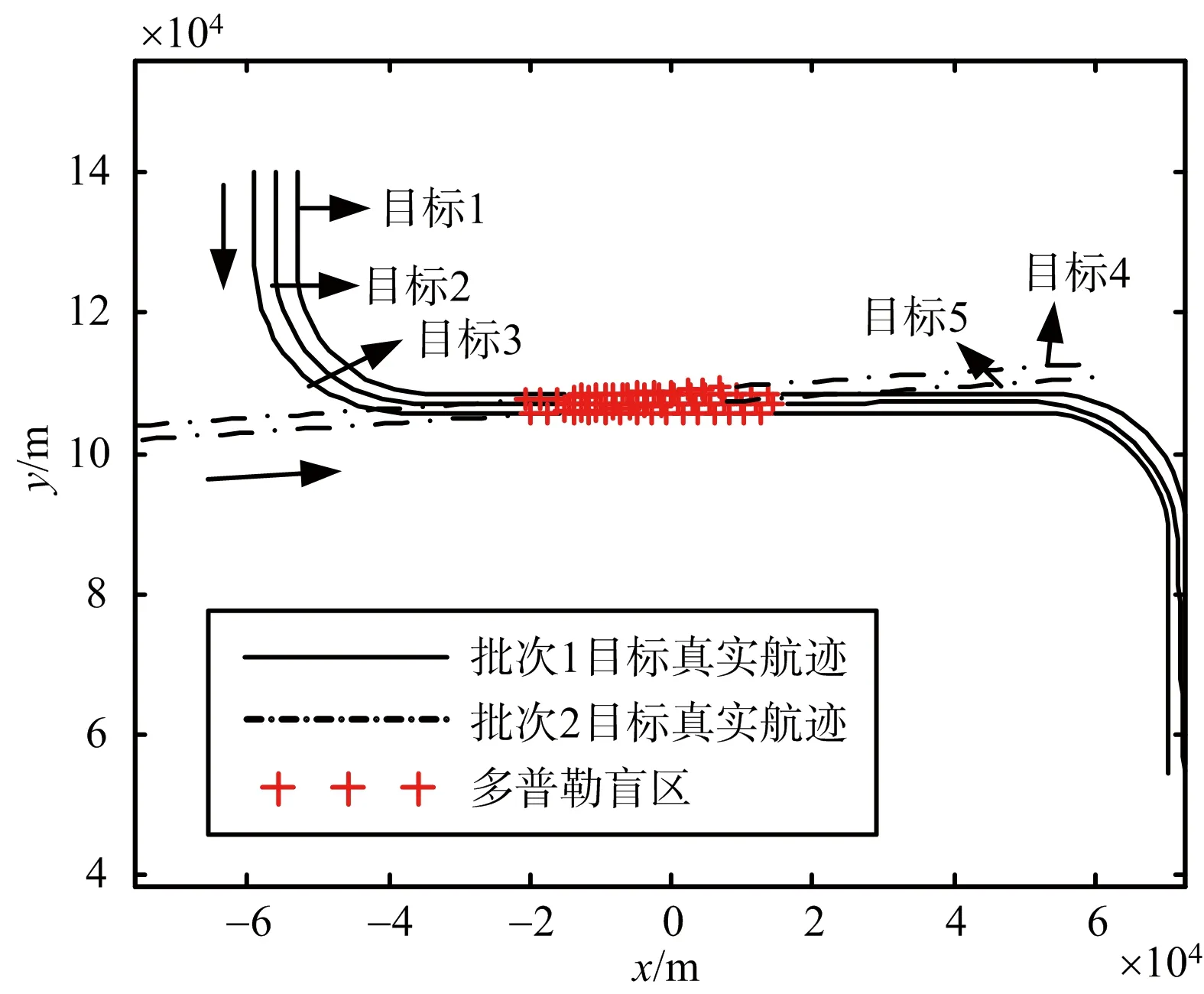
图3 目标真实轨迹及多普勒盲区分布

(26)

1) 高检测概率稀疏杂波情况(Pd=0.9，Pfa=1×10-5)

在高检测概率稀疏杂波情况下，针对目标2(批次1)和目标5(批次2)，4种算法的TB和MTL分别如表1和表2所示，图4为4种算法下两批目标的MTL对比情况。由于多普勒盲区范围超过撤销门限，在200次蒙特卡罗仿真中，如果不进行航迹片段关联，则航迹全部中断，从而也导致了较小的MTL。在采用IMM-EKF+航迹片段关联和IMM-BDPF+航迹片段关联后，两个目标的TB明显下降，MTL也明显增加。其中，采用了IMM-BDPF算法的航迹片段关联由于利用了多普勒盲区的先验信息，新老航迹的预测和逆向预测精度更高，其性能更好。但由于目标距离较近，且存在多普勒盲区条件下的交叉运动，仅利用运动学信息容易产生模糊，仍有少数情况发生航迹中断。而采用包含目标类别信息的航迹片段关联后，相较于仅利用位置信息的航迹片段关联，性能有了进一步的提升。对于目标2和目标5，该方法下的TB仅为1和2，即具有很高的正确关联率。

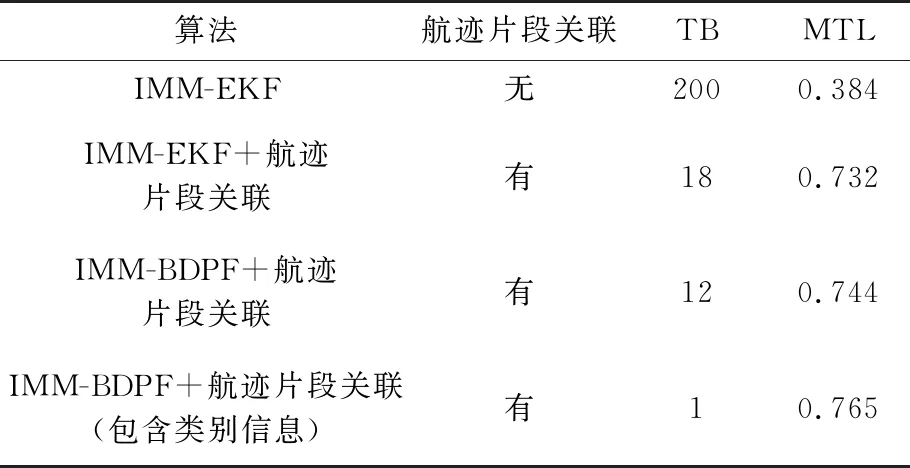
表1 4种算法下目标2的关联结果(Pd=0.9，Pfa=1×10-5)

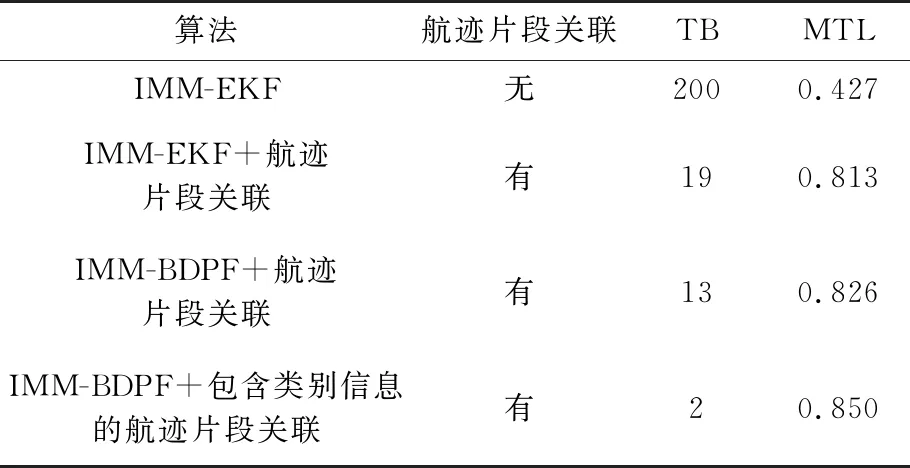
表2 4种算法下目标5的关联结果(Pd=0.9，Pfa=1×10-5)

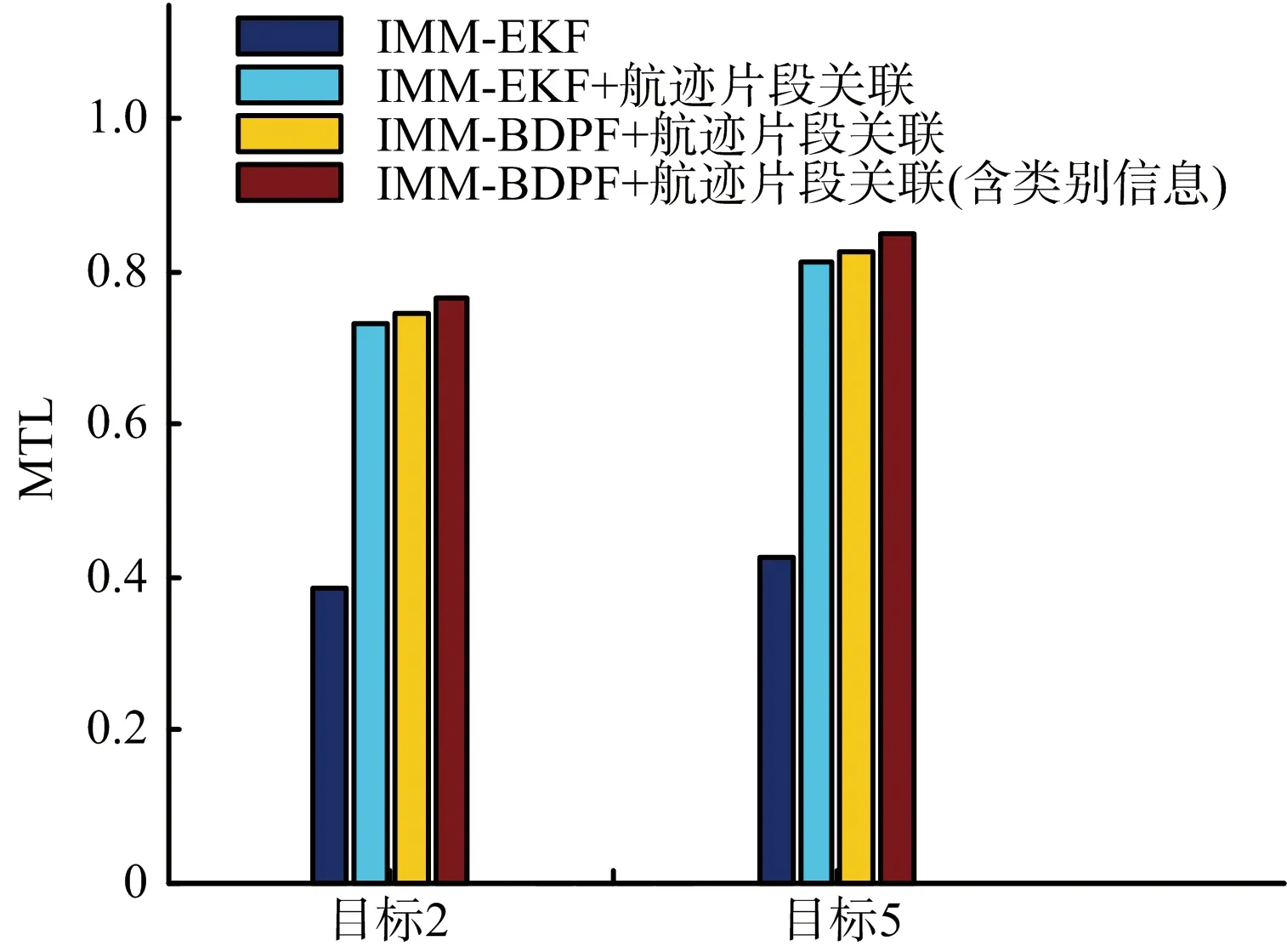
图4 4种算法的MTL(Pd=0.9，Pfa=1×10-5)

2) 低检测概率密集杂波情况(Pd=0.7，Pfa=5×10-3)

在低检测概率密集杂波情况下，针对目标2(批次1)和目标5(批次2)，4种算法下的TB和MTL分别如表3和表4所示，图5为4种算法下两批目标的MTL对比情况。同样，在采用IMM-EKF+航迹片段关联和IMM-BDPF+航迹片段关联后，两个目标的TB明显下降，MTL也明显增加。而采用包含目标类别信息的航迹片段关联后，性能有更进一步的提升。在低检测概率密集杂波环境中，利用运动学信息的航迹片段关联的性能普遍低于高检测概率稀疏杂波环境。这是由于低检测概率密集杂波环境下的目标跟踪精度相对较低，对新老航迹之间的分配产生影响，容易发生错误的关联。但该环境对于包含目标类别信息的航迹片段关联的性能基本没有影响。

表3 4种算法下目标2的关联结果(Pd=0.7，Pfa=5×10-3)

表4 4种算法下目标5的关联结果(Pd=0.7，Pfa=5×10-3)

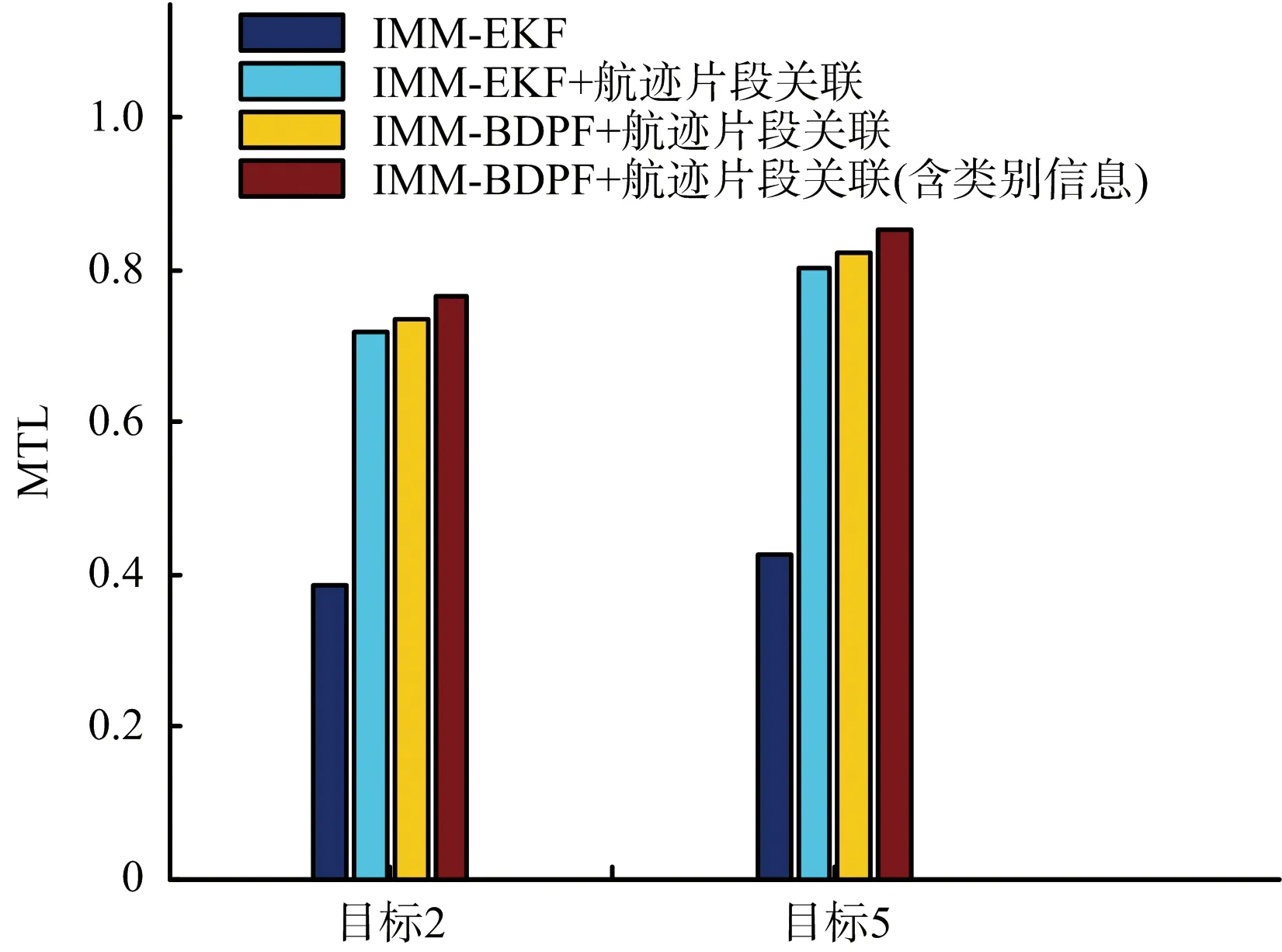
图5 4种算法的MTL(Pd=0.7，Pfa=5×10-3)

5 结束语

本文针对多普勒盲区条件下的多目标数据关联问题，提出一种新的基于二维分配的航迹片段关联方法，该方法将多普勒盲区先验信息并入到航迹片段关联中的航迹片段预处理和航迹片段初关联两个环节中，并将其他传感器获取的类别信息并入到二维分配代价函数中。仿真结果表明，利用了多普勒盲区先验信息后，航迹中断率明显低于未采用该信息的关联方法，航迹寿命明显延长，利用了类别信息的关联方法则有最低的航迹中断率和最高的航迹寿命。