仓储物流自动导引车轮系的设计
□ 孙鹏飞
沈阳新松机器人自动化股份有限公司 沈阳 110168
1 设计背景
自动导引车在自动化仓储及物流领域有着广泛的应用,根据应用领域可分为底盘合装车、叉车、巡检车、重载车等,根据功能形式可分为潜伏式、牵引式、辊筒式、背负式、搬运式等。应用最广泛的自动导引车是仓储物流自动导引车,其轮系通常由驱动轮组与随动轮组组成,依靠系统运动控制器、车体控制器、可编程序控制器等控制行走。其中,驱动轮组负责部分承载及驱动行走,随动轮组负责主要承载及一定情况下的转向功能[1-3]。
自动导引车轮系设计的关键是按照要求确定驱动轮组与随动轮组的数量及布局方案。数量由自动导引车负载决定,负载应为自动导引车自重与外部负载的总和。在数量确定的条件下,合理布局驱动轮组及随动轮组位置。由于自动导引车一般采用伺服电机驱动,电机与轮系为一体化结构,且大多整体从欧洲原装进口,成本较高,因此合理确定驱动轮组与随动轮组的数量,在自动导引车满足承载的条件下使驱动轮组与随动轮组均有合理的承载力及足够的驱动力,以保证自动导引车正常工作,具有足够的使用寿命,是自动导引车轮系设计的重点[4-7]。
2 轮系设计
根据轮系中驱动轮组与随动轮组的数量,轮系可分为三轮系、四轮系、六轮系、多轮系。一般在确定轮组总数量时,至少应满足三点确定一个平面的三轮系要求,以保证车体的稳定[8]。由于三轮系结构自身可确定一个稳定平面,因此不需要悬挂,在车体底盘整体加工及安装完成后保证车体水平即可。三轮系结构简单可靠,在自动导引车领域有广泛应用。三轮系结构可由一组驱动轮组与两组随动轮组构成,也可由一组随动轮组与两组驱动轮组构成,如图1所示。

▲图1 三轮系结构
背负式自动导引车三轮系负载通常比较大,为了获得可靠的驱动力,通常选用两驱一随布置形式。牵引式自动导引车三轮系通常负载比较小,为了获得最低成本,通常选用两随一驱形式。
对于四轮系结构而言,由于四点支撑不能确定一个稳定平面,因此为保证驱动轮组与随动轮组都能有效附着地面,构成一个稳定的车体底盘,需要增加悬挂系统。由于随动轮组相对驱动轮组有较大承载力,而驱动轮组一旦超越自身额定承载力将影响轮系寿命,甚至导致自动导引车无法行走,因此悬挂系统通常安装在驱动轮组上,既可以保证驱动轮组有一定承载力,又可以保证驱动轮组在承载一定正压力时产生足够驱动力,且不会因超载而缩短寿命。为保证车体足够稳定,需要有三个稳定支撑点。假设地面为理想平面,带有悬挂系统的驱动轮组在初始状态应为压死状态,即悬挂系统只能向下浮动,而不能向上浮动。
四轮系结构如图2所示。四轮系自动导引车通常用于大底盘、宽通道、大承载场合,且配置为两驱两随形式。两组驱动轮组单元在一定正压力下提供足够的驱动力,随动轮组用于承载剩余载荷。
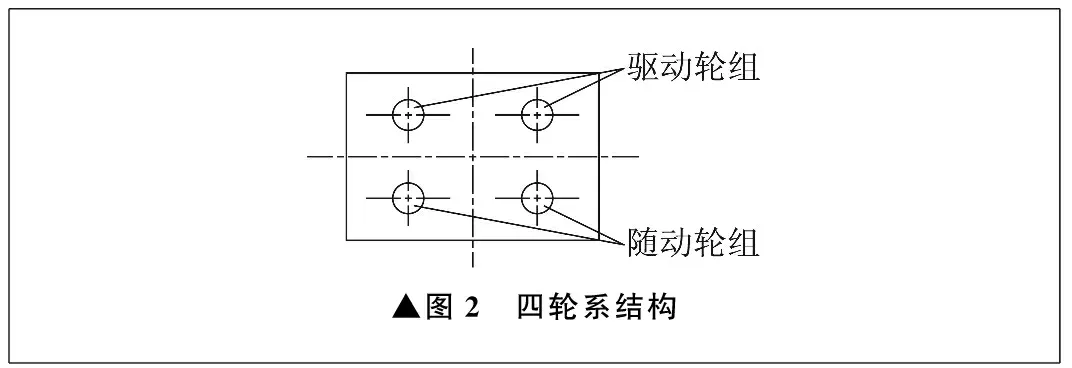
▲图2 四轮系结构
对于六轮系结构而言,通常设置为两组驱动轮组加四组随动轮组的形式。设置四组万向随动轮用以承载,四组万向随动轮中三组确定一个稳定平面。两组驱动轮组保证在一定正压力下产生足够驱动力,因此驱动轮组需增加悬挂系统。假设地面为理想平面,带有悬挂系统的驱动轮组在初始状态时应为悬浮状态,并有一定初始正压力,即悬挂系统既能向上浮动,也能向下浮动,以保证驱动轮组与地面有效接触。六轮系结构如图3所示。
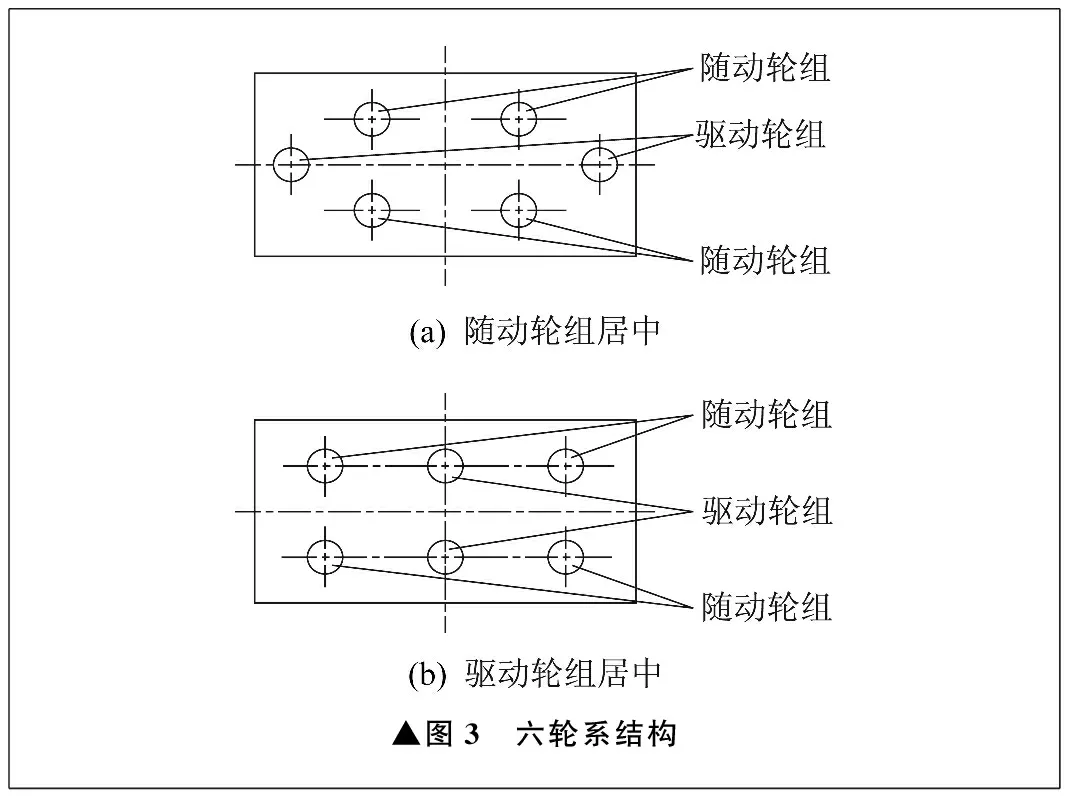
▲图3 六轮系结构
对于多轮系结构而言,四组随动轮组中由三组确定一个稳定平面以支撑车体,在三组随动轮组可以足够承载,且驱动轮组的驱动力又大于承载力的条件下,只需合理设计驱动轮组数量,以保证产生足够的驱动力。假设地面为理想平面,带有悬挂系统的驱动轮组在初始状态时均应为悬浮状态,并有一定初始正压力,即悬挂系统既能向上浮动,也能向下浮动,以保证驱动轮组与地面有效接触。多轮系结构常用于重载车,依靠多组驱动轮组产生足够的驱动力,随动轮组通常只有四组。
3 随动轮组设计
随动轮组分为带舵随动轮和不带舵万向随动轮两种。带舵随动轮可以自主打舵控制随动轮方向,并且在行驶过程中通过伺服电机实时调整随动轮组的转动角度。不带舵万向随动轮只能被动行走,且在行驶过程中被动实时调整角度。随动轮依据现场使用环境而选择,若现场需具备前进、倒退、转弯、自旋等功能,则随动轮需设计为带舵随动轮,以便自动导引车可以完成上述动作。可以完成上述动作的自动导引车也称全方位自动导引车。
随动轮轮片主要为定制铝毂表面包覆聚氨酯层等耐磨材料,其承载力随速度的加快而减小。若随动轮组数量不足以承受负载,则可以将单个随动轮组设计为双轮片形式,以避免单个轮片负载能力不足的情况。因此,大多数工况下,不存在随动轮组负载能力不足的问题。
4 驱动轮组设计
驱动轮组承载力主要来自悬挂系统压缩弹簧产生的正压力,该正压力是自动导引车驱动力的来源,因此带有悬挂系统的驱动轮组在初始状态时应为压缩状态,以便保持一定的初始正压力。正压力产生的摩擦力是整个自动导引车驱动力的来源,至于能否驱动,则取决于电机与轮系为一体化结构的驱动轮组的伺服电机。可见,匹配驱动伺服电机是轮系设计中的一个重要环节。
5 伺服电机选型
伺服电机匹配对于自动导引车轮系设计有重要意义,伺服电机直接影响自动导引车灵敏度、伺服系统精度、安装空间大小及成本等。匹配伺服电机一般需要考虑四个因素,即减速机、速度、容量、转动惯量。
5.1 减速机
减速机与伺服电机转速、容量、转动惯量等基本参数的确定相辅相成,互相影响,需要综合考虑。电机最快转速决定了配套减速机减速比的上限,电机最大扭矩则限制了配套减速机减速比的下限,且减速机减速比直接以二次方的关系放大了应匹配的伺服电机的转动惯量[9]。
5.2 速度
在实际使用环境中,为了满足最慢节拍要求,需要自动导引车达到一定速度。自动导引车要求最慢行走速度为v,轮径为D,配套减速机减速比为i,则电机转速n需满足[10]:
n≥vi/(πD)
(1)
5.3 容量
对于自动导引车而言,需要驱动伺服电机输出足够大的扭矩,以克服行驶过程中摩擦阻力产生的力矩,即电机容量应满足驱动力要求。由于现场对电机的适用工况很难预先量化,因此可以简化考虑驱动力矩是否满足驱动要求,并留有一定余量,实践证明这一方法简易可行。
驱动轮片表面包覆材料一般为聚氨酯,对应滚动摩擦因数通常为0.3,静摩擦因数可达0.5。计算伺服电机输出扭矩时,需要校核电机启动输出扭矩是否能满足静摩擦因数下的启动要求。
自动导引车行驶时,额定输出扭矩克服轮片与地面滚动摩擦阻力所产生的力矩MA,MA为:
MA=0.3mgDiN/2
(2)
式中:N为轮系驱动轮数量;m为整车质量;g为重力加速度。
考虑到系统余量,一般取1.1MA以上进行校核。
自动导引车启动时,最大启动力矩克服轮片与地面瞬间静摩擦阻力产生的力矩MB,MB为:
MB=0.5mgDiN/2
(3)
考虑到系统余量,一般取1.1MB以上进行校核。
5.4 转动惯量
为了使自动导引车运行稳定、可靠,需计算自动导引车在行驶中折算为伺服电机输出轴的等效转动惯量[JL],[JL]为机构中所有直线运动部件等效换算的转动惯量JL1与所有旋转运动部件的转动惯量JL2之和。根据能量守恒定律,有:
(4)
式中:v1为直线运动速度;ω为伺服电机转动角速度。
自动导引车整车直线运动部件等效换算的转动惯量[J]为:
(5)
对于自动导引车通过伺服电机直接带动减速机驱动轮片行走的结构,有:
[JL]=mr2+JL2
(6)
式中:r为驱动轮片半径。
旋转部件转动惯量JL2实际仅为减速机转动惯量JL0,因此单驱动电机输出轴等效转动惯量JL为:
JL=JL1/N+JL0=mr2/N+JL0
(7)
减速机转动惯量JL0可通过减速机样本进行查询。
转动惯量对伺服系统的精度、稳定性及动态响应都有影响。转动惯量越小,系统的动态特性越好。转动惯量越大,系统的机械常数越大,响应越慢,影响伺服精度和响应速度。适当增大转动惯量,只在改善低速爬行时有利。自动导引车系统的负载等效转动惯量需和伺服电机转动惯量相匹配,不同的系统对应的转动惯量匹配原则不同,但多数情况下均要求电机输出轴等效转动惯量JL与伺服电机转动惯量JM的比值小于10,自动导引车系统的伺服电机转动惯量一般按JL/JM不大于4来匹配。
6 结束语
自动导引车轮系设计时,首先确定使用功能及整车负载,然后按承载力确定轮系结构,并布局驱动轮组与随动轮组的空间位置。按自动导引车参数匹配驱动轮组伺服电机及轮径等,完成驱动轮组的选型,最终完成自动导引车轮系的设计。

