自锚式悬索桥拉-吊体系转换中索力力学特性
何 立,吴海军,王邵锐,郭 辉
(1. 重庆交通大学 a. 土木工程学院;b. 省部共建山区桥梁及隧道工程国家重点实验室,重庆 400074;2. 铁科院(北京)工程咨询有限公司,北京 100081)
相较于地锚式悬索桥,自锚式悬索桥因主缆直接锚固在梁端而不需庞大的锚碇,对地质环境要求较低,结构新颖、造型美观,是大跨径桥梁设计最青睐的结构体系之一[1~3]。自锚式悬索桥一般采用支架或临时墩架设主梁并实现体系转换,这对通航流域有较高要求,限制了其发展。为了满足少支架甚至无支架的技术要求,业界创造性地提出了“先斜拉,后悬索”的体系转换方式[4,5],但针对此特殊施工法国内外均无成熟经验可借鉴,相关研究也鲜有报道。
目前,针对大跨径自锚式悬索桥索力力学特性已有部分学者进行了相关研究,如黄海云等[6]通过模型试验分析了猎德大桥吊索索力变化规律及探讨了吊索索力弱相干性的适用条件;沈锐利等[7]利用吊索索力影响线对吊索的受力行为进行了研究;王桢等[8]采用模型试验与数值模拟相结合的方法分析了桃花峪黄河大桥的索力相邻影响性及成桥索力来源。但以往的研究均是基于传统体系转换方式,且集中在索力张拉规律及相邻影响性上,而“先斜拉,后悬索”施工法为首次运用于桥梁建设中,工程界对此特殊体系转换过程中临时斜拉索与吊索索力变化规律以及吊索索力变化的几何非线性行为表现等认识不够深入和全面,特别是当自锚式悬索桥跨径从400 m级突破至600 m级时其结构体系力学特性发生了巨大变化,且随着跨径的增长几何非线性问题也更加显著,这就决定了研究大跨自锚式悬索桥在“先斜拉,后悬索”体系转换过程中索力力学行为特性是有必要的。有鉴于此,本文以鹅公岩轨道专用桥为背景,对此特殊体系转换过程中索力力学特性进行研究,以期为工程界增添新的经验与认识,也可为同类型桥梁的建设提供参考。
1 工程概况

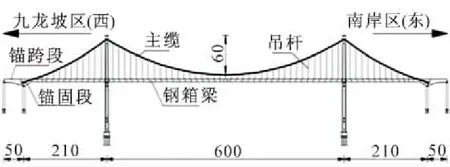
图1 全桥桥跨布置图/m
总体施工思路:边跨采用顶推施工法,中跨采用斜拉扣挂悬臂施工法安装钢箱梁并形成斜拉桥体系;再以此为基础架设主缆、张拉吊索形成“斜拉-悬索”共存体系;最后通过卸除临时斜拉索转换成悬索桥体系。
2 数值模拟方法
采用MIDAS Civil有限元分析软件建立“斜拉-悬索”体系转换计算模型。结合实际情况,主塔、主梁采用变截面梁单元模拟,临时钢塔采用等截面梁单元模拟,主缆、吊索、斜拉索用只受拉索单元模拟;主塔下端固结,主梁与主塔交接处考虑采用竖向与横桥向限位约束,支撑主梁的临时支架采用只受压不受拉的弹性连接,有限元分析模型见图2。

图2 MIDAS Civil有限元模型
斜拉桥与悬索桥为两个独立的结构体系,二者可通过无应力状态法实现耦合[9]。值得注意的是,斜拉桥成桥线形是以悬索桥成桥线形为目标线形完成临时斜拉桥体系后,通过调整斜拉索索力来调整主梁线形至其接近去二期恒载线形。主塔塔顶主索鞍可通过设置温度杆单元等效模拟,为精准顶推,使温度杆受温度作用时主塔及主缆对其约束影响忽略不计,温度杆弹性模量取值应远大于主塔及主缆,通过对温度杆升、降温来实现主索鞍的预偏及顶推。
3 索力力学特性分析
本文所采用的体系转换程序是综合施工便利性、安全性、经济性等原则而设置,在整个施工过程中各构件受力及变形均符合要求。
鹅公岩轨道专用桥桥跨呈对称布置,在施工过程中全桥两岸索力变化规律基本一致,故仅取西岸(九龙坡区侧)索力数据进行分析。此桥吊索编号及临时斜拉索编号如图3所示,图中:LS,LM,M0分别指左边跨吊索、左中跨吊索和跨中吊索编号;RS,RM分别指右边跨吊索、右中跨吊索编号;斜拉索编号由长索到短索依次为16#~1#。体系转换施工工序见表1。

图3 “斜拉-悬索”体系共存图示

表1 体系转换施工步骤

(续表)
3.1 吊索索力变化规律分析
在“斜拉-悬索”体系转换过程中,边中跨吊索索力安全系数满足规范要求(≥2.5),西岸(九龙坡区侧)边、中跨部分吊索索力变化规律如图4所示,分析如下。
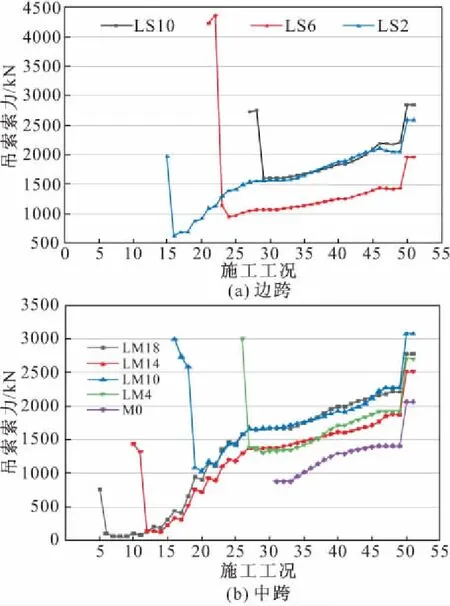
图4 部分吊索索力变化规律
边中跨吊索均因吊索张拉而获得索力,在相邻吊索张拉影响下其索力骤减,各吊索力最大减小量占成桥索力比值约为:边跨39.4%~156.7%,中跨24.0%~72.5%;非相邻吊索的张拉促进了其索力累积增长,各吊索力增长最大值占成桥索力比值约为:边跨0.3%~7.3%,中跨0.1%~10.0%。由此可见,张拉吊索对其相邻吊索索力削减程度较大,对其非相邻吊索索力影响小但不可忽略。
在主索鞍顶推工况(如工况8,17,25等),边跨吊索索力增大,中跨吊索索力减小。悬索桥施工中鞍座顶推的目的是释放鞍座底由于桥塔纵向刚度约束引起的纵向剪力,避免桥塔受力过大和主缆在鞍座中的滑移。一般悬索桥鞍座顶推前后主缆线形变化不大。本桥由于先施工了斜拉桥,临时拉索及钢塔对永久主塔纵向位移有较大约束作用,增大了永久主塔的抗推刚度。因此顶推主索鞍使塔顶两主索鞍之间的水平距离缩小,边跨主缆水平距离增大,即中跨主缆呈现出“松弛”状态,边跨主缆呈现出“紧绷”状态,促使中跨主缆至桥面的距离缩短,边跨主缆至桥面距离变大,从而导致边跨吊索索力增大,而中跨吊索索力减小。
在拆除临时斜拉索阶段,边、中跨吊索索力变化曲线经历了先徐徐上升、后趋于平稳两个阶段。这主要是因为随着临时斜拉索拆除,初始由拉索承担的主梁重量转移至了吊索,促使吊索索力逐渐增大;在体系转换末期,主缆重力刚度基本形成,主缆竖向刚度较大,拆除拉索对主缆竖向位移影响较小,因此在临时拉索拆除末期,吊索索力增量小、索力比较稳定。
3.2 临时斜拉索索力变化规律分析
在“斜拉-悬索”体系转换过程中,边中跨拉索索力安全系数满足规范要求(≥2.5),西岸(九龙坡区侧)边、中跨部分临时斜拉索索力变化规律如图5,分析如下。
在吊索张拉阶段,边、中跨临时拉索索力随吊索张拉而逐渐削减,这主要是由于初始由临时斜拉索承担的主梁重量部分由吊索分担,从而缓慢地削减了拉索索力。受邻近吊索张拉的影响,中跨斜拉索索力削减量显然大于边跨,这主要是因为边跨斜拉索下端锚固在自重较大的混凝土梁段上,而中跨斜拉索下端锚固于自重相对较轻的钢箱梁顶部,吊索张拉使中跨主梁线形提升量大于边跨,故而中跨斜拉索索力削减量较边跨显著。
塔顶主索鞍顶推使边跨斜拉索索力减小,中跨斜拉索索力增大。主要是由于斜拉索上端锚固在临时钢塔上,临时钢塔固结于永久塔顶部,主索鞍顶推使临时钢塔跟随永久塔向河岸侧偏移,导致边、中跨斜拉索呈现出与吊索相反的状态,即边跨拉索“松弛”、中跨拉索“紧绷”,从而导致边跨斜拉索索力减小,中跨斜拉索索力增大。
在临时斜拉索拆除阶段,边、中跨未拆除拉索的索力随着邻近拉索拆除而逐渐增大,临时斜拉索在拆除之际仍承担着主梁的部分重量,此刻边、中跨绝大部分斜拉索索力占斜拉桥成桥索力比值约为40%~60%,斜拉索残留较大的索力增加了拆除拉索的施工风险,这也就决定了临时斜拉索由上而下的拆除顺序是更合理的。
3.3 吊索索力几何非线性行为分析
在“斜拉-悬索”体系转换过程中,由于张拉吊索,主缆将不断寻找新的平衡状态,主缆变位与吊索索力间呈现显著的几何非线性关系,主缆变位导致主缆刚度变化,同时伴随吊索的伸长量变化,吊索的索力也相应地发生了改变,即吊索索力的几何非线性变化源于主缆。因此,对吊索索力几何非线性变化研究的同时也能对主缆的几何非线性予以表征。
大跨径自锚式悬索桥几何非线性问题尤为突出,研究非线性的方法较多[10,11],本文采用最为直接的方法——分次加载法对吊索索力变化随施工阶段表现出的几何非线性行为特性进行研究。分次加载法是以荷载作用不发生改变为原则,探求结构响应的变化规律。具体陈述为:在同一结构体系中、同一施工工序下,将同一位置的作用荷载均分为两份,连续两次作用于结构,对比吊索索力增量。若两次增量相同,则吊索索力的变化呈为线性特征;否则,其表现为几何非线性特性。
应用以上方法,将各工况中的作用均分为两份,依次作用于结构,此时吊索索力将产生两次增量,各工况下吊索索力增量差值最大值如图6所示,分析如下。
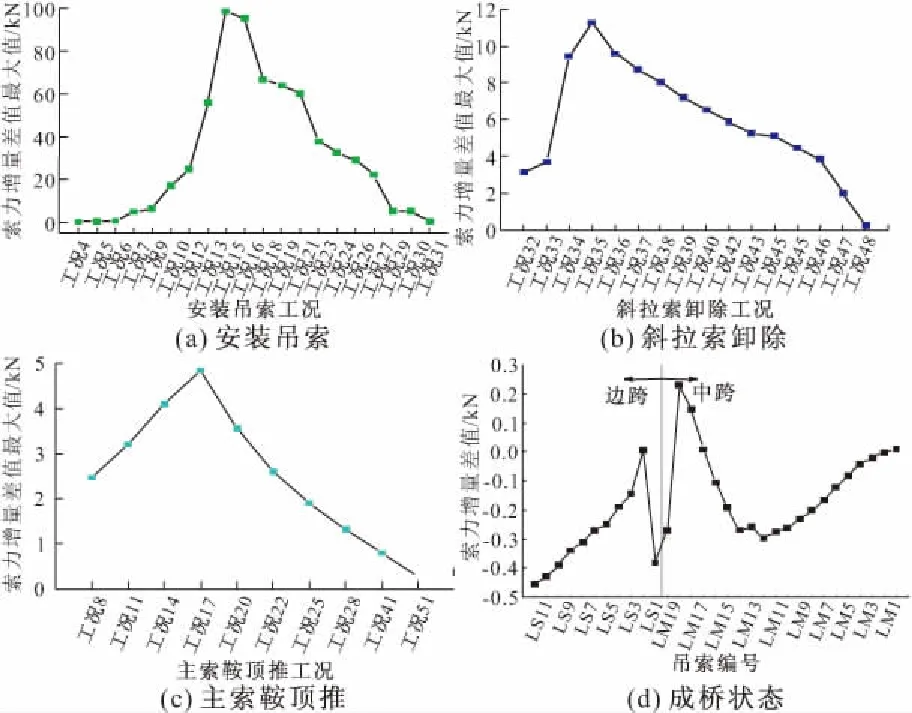
图6 吊索索力几何非线性特征
在图6a中,工况4~12为张拉中跨近塔区能一次张拉到位的吊索,在各吊索张拉工序作用下,吊索索力增量差值最大值从0.26 kN逐渐增至24.65 kN;工况13~31为张拉边、中跨吊索,两侧同步张拉,随着吊索张拉的进行,吊索索力增量差值最大值主要历程为:55.72→98.47→0.43 kN。由此表明,在吊索安装过程中吊索索力经历了几何非线性特征增强、线性特性弱化→线性特性增强、几何非线性特性衰减两个阶段。
在图6b中,工况32~48为拆除临时斜拉索阶段,在此过程中吊索索力增量差值最大值主要历程为:11.25→0.28 kN。这说明了在临时斜拉索拆除过程中吊索索力的几何非线性特性进一步弱化,线性特性愈发明显。
由图6c可知,在吊索张拉前期,主索鞍顶推作用下吊索索力增量差值最大值随施工工况进行而逐步增大;在吊索张拉后期及拆除斜拉索阶段,其量值依次减小。这表明了在主索鞍顶推过程中吊索索力的几何非线性呈现出“先由弱到强,再从强变弱”的变化规律,但索力增量的量程较小,且“由弱到强”仅持续了3个工况,因此在临时拉索拆除过程中吊索索力的几何特性以线性为显性。
图6d表明,将二期恒载均分为两份施加在主梁上,两次荷载作用下吊索索力增量差值波动范围为:-0.46~0.28 kN。由此表明,悬索桥成桥后,在恒荷载作用下,吊索索力变化呈显著的线性特征,此时线弹性叠加原理适用。
4 结 论
鹅公岩轨道专用桥采用“先斜拉,后悬索”以实现体系转换的方法为业界首次尝试,方案新颖,施工难度极大。基于此工程背景,探讨了大跨自锚式悬索桥在“斜拉-悬索”体系转换过程中索力力学特性,得出以下主要结论:
(1)在“斜拉-悬索”体系转换过程中,边、中跨吊索索力大致经历了5个阶段:因张拉而获得索力;张拉相邻吊索使其索力骤减;张拉非相邻吊索使其索力累积增加;拆除斜拉索使其索力缓慢增长;主索鞍顶推使边跨索力增大,中跨索力减小。体系转换完毕后,施工二期铺装使索力显著增长。
(2)在“斜拉-悬索”体系转换过程中,边、中跨临时斜拉索索力大致经历了3个阶段:吊索张拉使拉索索力逐渐削减;临时斜拉索的拆除使未拆除拉索索力缓慢增长;主索鞍顶推使边跨索力减小,中跨索力增大。
(3)在整个体系转换中,吊索力的几何非线性行为呈现出“先由弱到强,再从强变弱”的总体变化趋势。具体表现为:在吊索安装阶段,吊索索力表现出由几何非线性特征增强、线性特性弱化向线性特性增强、几何非线性特性弱化转变的规律;斜拉索的拆除使吊索索力的几何非线性特性进一步衰减;主索鞍顶推及成桥恒荷载作用下,吊索索力变化表现为显著的线性特征。

