基于多源域迁移学习的脑电情感识别
娄晓光,陈兰岚,宋振振
(华东理工大学 信息科学与工程学院 化工过程先进控制和优化技术教育部重点实验室,上海 200237)
0 引 言
情感智能[1]是人与人之间交流过程中不可或缺的一部分,情感状态识别是情感研究工作中的核心内容。相较于其它方法,脑电信号灵敏度较高,能够无视被试的情感伪装,能直接反映与情感变化相关的大脑内在状态,因此越来越受到研究者的青睐。Li Mi等[2]提取脑电5个频带的能量信息作为特征,计算不同频带下导联与情感的相关性,分析得出与情感状态强相关的脑区与频带。
传统的机器学习中要求训练数据和测试数据必须服从独立同分布的约束条件,然而脑电信号存在很强的个体差异性,不同被试即使表达相同情感对应产生的脑电特征也不尽相同,而迁移学习放宽了训练数据和测试数据服从独立同分布的限制[3],所以利用迁移学习可将从先前被试身上学到的知识或模式应用到另一个新被试上,挖掘出源域被试和目标被试间共享的信息,最终构建适应目标被试数据分布的模型。
对于单源域迁移学习,如果领域间的相关性较低,直接迁移可能会产生负迁移现象[4],并且在进行跨被试情感识别时往往存在多个源域被试数据,因此可以利用多源域迁移学习来弥补单源域迁移学习的不足。目前鲜有文献从样本和特征两个层面对待迁移的多源域数据进行优化的报道,本文提出用多源域选择(multi-source domain selection,MDS)与迁移特征选择(transfer feature selection,TFS)相结合的方式得到适宜迁移的数据,在此基础上利用基于适配正则化线性回归的迁移学习算法[5](adaptation regularization regularized least squares,ARRLS)对跨被试的情感数据进行建模。
1 情感识别总体框架
针对多源域迁移学习问题,一种做法是将所有源域合并为一个大源域,另一种做法是将每个源域单独考虑,训练多个子模型并将之集成。前者忽略了不同源域间的差异性导致建立的模型性能较差,后者需要建立多个迁移模型,往往计算时间过长,且其中存在与目标域相似度较低的源域个体,其模型在集成过程中会影响总体的识别精度。因此多源域数据的优化选择及集成学习是一个值得研究的问题。Liu等[6]在全局层面将不同域视为一个整体并缩小源域与目标域间的差异,在局部层面分析不同域间的关系以最大化分类性能。K Vogt等[7]对多个源域赋予不同权重,使模型合理利用源域间的信息,以促进目标域的学习。
本文构建的情感识别模型如图1所示。首先对原始信号滤波并提取差分熵特征[8],其次利用MDS-TFS-ARRLS算法构建情感识别模型。该模型的构建分为4个步骤,前两步主要解决“什么样的知识适合于迁移”的问题,即对待迁移的多源域数据进行优化;后两步主要解决“知识如何迁移”的问题,即采用合适的迁移学习及集成学习算法。第一步利用多源域选择算法(MDS)全面度量目标域与其对应的各个源域的相似性大小,从多个源域中过滤掉可能会导致负迁移现象的部分源域,保留最优的源域集合,降低仅用单一源域数据进行迁移带来的风险,同时节约计算成本;第二步利用迁移特征选择算法(TFS)从多个源域中寻找共同有效的特征子集,增强特征推广性,从而使数据具有更好的迁移能力;第三步利用适配正则化线性回归算法(ARRLS)构建多个迁移学习模型,最后根据每个模型所对应的源域与目标域间的相似性大小分别赋予其不同权重建立集成迁移学习模型。
下面对MDS-TFS-ARRLS算法中各个环节分别进行介绍。

图1 情感识别模型总体框架
2 算法介绍
2.1 多源域选择算法(MDS)
本文提出了一种多源域选择算法(multi-source domain selection,MDS),该算法目的在于通过领域间相似性的度量,从多个源域中筛选出与目标域较为相似的源域集合。考虑到仅从域-域层面度量相似性具有片面性,因此该算法又从样本-域层面度量相似性大小。MDS算法首先计算域-域和样本-域两个层面的相似性,然后将这两个层面的相似性值组成源域和目标域的联合相似度矩阵,并使用K-means算法对联合相似度进行聚类,自适应选取最优源域集合。其中,域-域相似性是基于领域间整体均值的差异,样本-域相似性是基于所有目标域样本到源域的距离之和。MDS算法的计算过程如图2所示,下面分别对相似性的计算和最优源域集合的选取做出介绍。

图2 MDS算法流程
2.1.1 域-域相似性计算
领域间整体数据差异在于两者概率分布的不同导致数据分布的不同,常用的概率分布距离度量函数有相对熵[9]、布雷格曼散度[10]和最大均值差异(maximum mean discre-pancy,MMD)[11]。前两种方法计算通常需要估计其分布密度,而最大均值差异可以用不同领域在无限维核空间中的均值差异来近似,计算相对简单且效率高,因此该方法的使用最为广泛。本文采用MMD将源域和目标域数据嵌入到共享的可再生希尔伯特空间中,在该空间中两者间的均值差异代表相似度大小。MMD计算值越大代表领域间相似性越大。
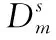
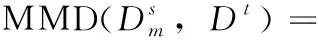
(1)
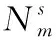
(2)
其中,Ki,j=〈φ(xi),φ(xj)〉, 本文中采用线性核。L矩阵可由式(3)求得
(3)
2.1.2 样本-域相似性计算
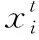
(4)
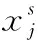
(5)
2.1.3 联合相似性度量及聚类
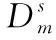
(6)
本文利用K-means算法对相似度特征聚类,并将聚类数K取为2、3、5来分别确定其不同大小的最优源域集合。并进一步根据相似度向量的模值大小计算最优源域集合中每个源域的权重ωm。ωm计算公式如下
(7)
2.2 迁移特征选择算法(TFS)
为了进一步降低后续迁移学习的计算成本、提高识别精度,本文使用迁移特征选择算法筛选出适宜迁移的特征子集,该算法由两个阶段组成,其计算流程如图3所示。
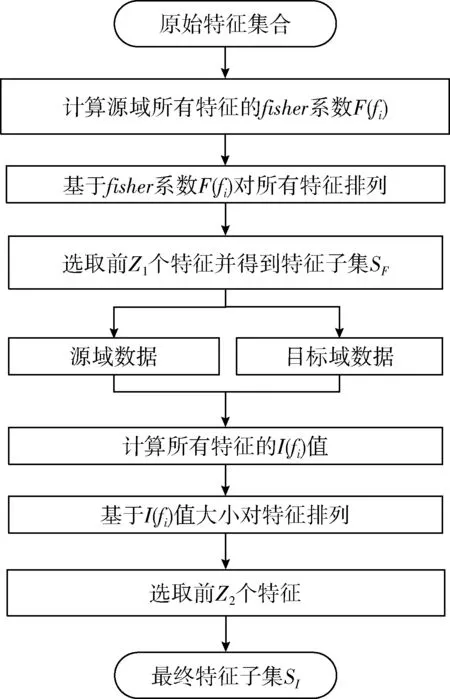
图3 TFS算法流程
首先计算源域中每个特征对应的Fisher Score[13]值,Fisher Score属于过滤型特征选择算法,具有计算速度快适用性强的优点。该算法通过度量样本中类间散度与类内散度的关系,判断特征与类别标签间的相关性。本文根据Fisher Score准则选取具有鉴别力的特征集合。Fisher Score的计算公式如下
(8)
其中,C为样本类别数,特征fi的平均值为μi,nj为第j类样本个数,μij和σij为第j类样本特征fi的平均值与标准差。
迁移特征选择算法第二部分通过衡量特征与域标签之间的相关性来选取源域与目标域之间更具一致性的特征。通常特征选择利用互信息来定义特征与类别标签间的相关性[14],本文通过互信息来衡量特征与域标签之间的相关性,源域数据标签为S,目标域数据标签为T。常用的相关性度量方法有Pearson相关系数和Spearman相关系数,但上述两种方法只能度量变量间的线性关系,而互信息可以衡量非线性关系,并且对噪声信号具有很好的鲁棒性。此外,Pearson和Spearman相关系数的计算要求源域和目标域样本具有相同的实验采集顺序,而利用互信息没有该限制。互信息值越大代表两组变量越相关,因此互信息值I(fi) 越小代表特征fi与域标签间的相关性越小,则在该特征表示下,领域间的差异较小。样本x, y的概率密度与联合概率密度计算互信息
(9)
图4为利用互信息计算特征与域标签相关性示意图,根据每个特征互信息的值对其排序,选取相关性较小的部分特征组成最终特征集合,该特征集合不仅具有良好的可分性,且能够更好地反映出源域与目标域数据间的共享信息。
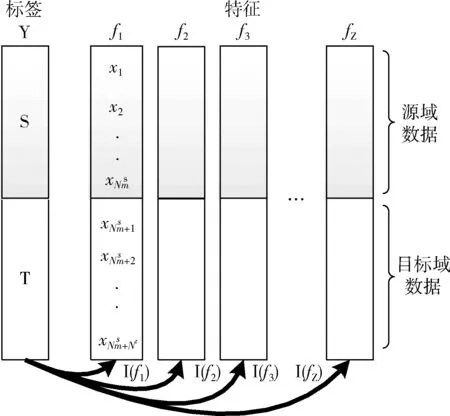
图4 特征与域标签相关性计算
2.3 适配正则化线性回归算法(ARRLS)
迁移学习根据迁移的方式不同可分为:基于实例迁移、基于特征迁移、基于参数迁移和基于相关知识迁移。本文采用一种基于特征的迁移学习——适配正则化线性回归算法(ARRLS)[5],该算法同步优化结构风险泛函、联合分布距离、流形不一致性等学习准则[4],同时能够缩小领域间的数据结构差异。其学习框架如式(10)所示

(10)
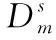
3 实验及结果分析
3.1 实验数据
实验环境:Intel(R) Core(TM) i7-8750H CPU @2.20 GHz,8 G内存,64位Windows10系统,算法的实现采用64位MATLAB R2016b。
本文以公开数据集SEED(SJTU Emotion EEG dataset)作为研究对象。根据国际10-20系统,使用62个通道的ESI-NeuroScan系统记录脑电信号,采样频率为1000 Hz。该数据集了记录了15名被试(包括7名男性8名女性)观看不同类型视频片段所采集的脑电数据。每名被试参加3次实验,时间间隔约为1周,共得到45组测试数据。被试观看的视频片段共分为3个不同情感类别,分别为Positive,Neutral,Negative[15],每次实验过程中视频开始前有一个5 s提示,表示视频的开始,视频结束后会有45 s的自我评估,最后有15 s的休息时间,观看时长约为4 min。
本文取每名被试第1次实验所得的15组实验数据作为分析使用。将初始脑电信号降采样至200 Hz,并将每1 s的实验数据作为一个样本,最终每名被试数据可得到3394个样本。在5个频带上(delta:1 Hz-3 Hz, theta:4 Hz-7 Hz, alpha:8 Hz-13 Hz, beta:14 Hz-30 Hz, gamma:31 Hz-50 Hz)分别提取脑电信号的差分熵特征[11],因此,每个样本共有5×62(频带×导联)=310维特征。其中差分熵的计算公式如下所示
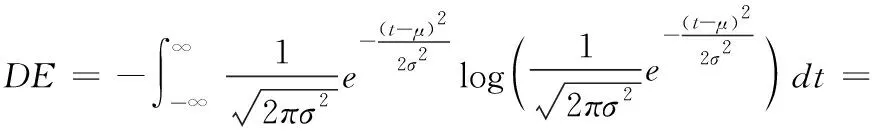
(11)
其中,t表示来自EEG信号的子带信号,设该信号服从高斯分布N(μ,σ2)。 文献[16]中证明原始观测信号经过带通滤波后,其子带信号的时间序列大致遵循高斯分布。
3.2 ARRLS算法性能分析
由于源域与目标域数据分布不同,如果直接从源域中划分出数据作为验证集确定算法的参数,通常会导致较差的测试集实验结果[10]。因此本文在一定范围内进行了参数搜索,展示和对比了每种算法的最佳结果。这里SVM采用Lin开发的工具包LIBSVM[18],其惩罚参数c在{2-5~25}内搜索最优结果,最终本文设置c=4。 TCA算法中γ,λ在{2-5~25}内分别搜索最优结果确定γ=1,λ=1。 ARRLS算法中参数采用基于分层网格搜索的优化方法。首先将λ,γ参数在{2-5~25}内搜索分别设置λ=1,γ=1, 其次将σ在 {0.001,0.01,0.1,0,1,10} 内搜索后确定σ=0.1, 迭代次数设置为5。
表1中比较了ARRLS、SVM和TCA这3种算法的平均识别精度,图5则更为详细地展示了这3种算法的个体识别精度。从表1中可以看出,ARRLS在两种核函数下均具有最优的平均实验结果,且迁移学习算法在跨被试实验中实验结果强于SVM分类器。从图5中可看出ARRLS算法在大多数个体上具有出色的识别精度。综合分析上述实验结果,由于SVM分类器算法仅利用训练集数据构建模型,而该模型并不能适配于测试集数据分布,因此难以取得理想实验结果。TCA算法虽然将数据投影到核空间中减少不同被试间边缘分布差异,但未能考虑到被试间条件分布也存在差异,并且未能同时优化损失函数与流形正则化,从而导致结果仍然不理想。ARRLS同时最小化损失函数、联合概率分布函数、流形正则化,因此ARRLS方法在平均和个体识别结果上均表现良好且更稳定。但从表1中可以看出ARRLS算法虽然识别精度高,但存在计算时间过长的问题。
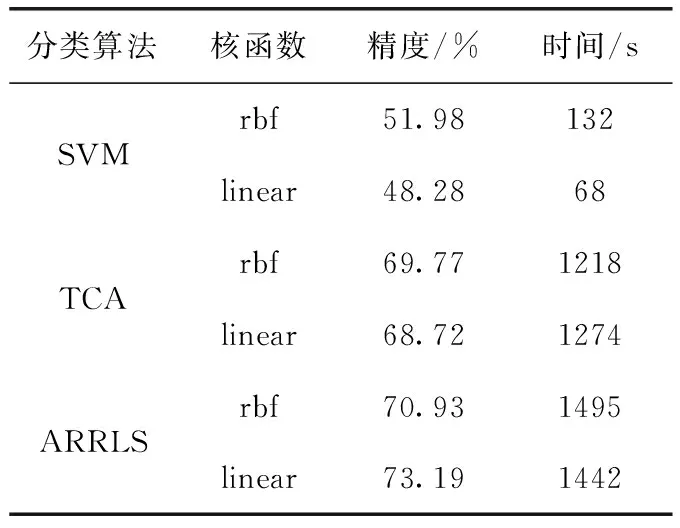
表1 不同分类算法的情感识别结果
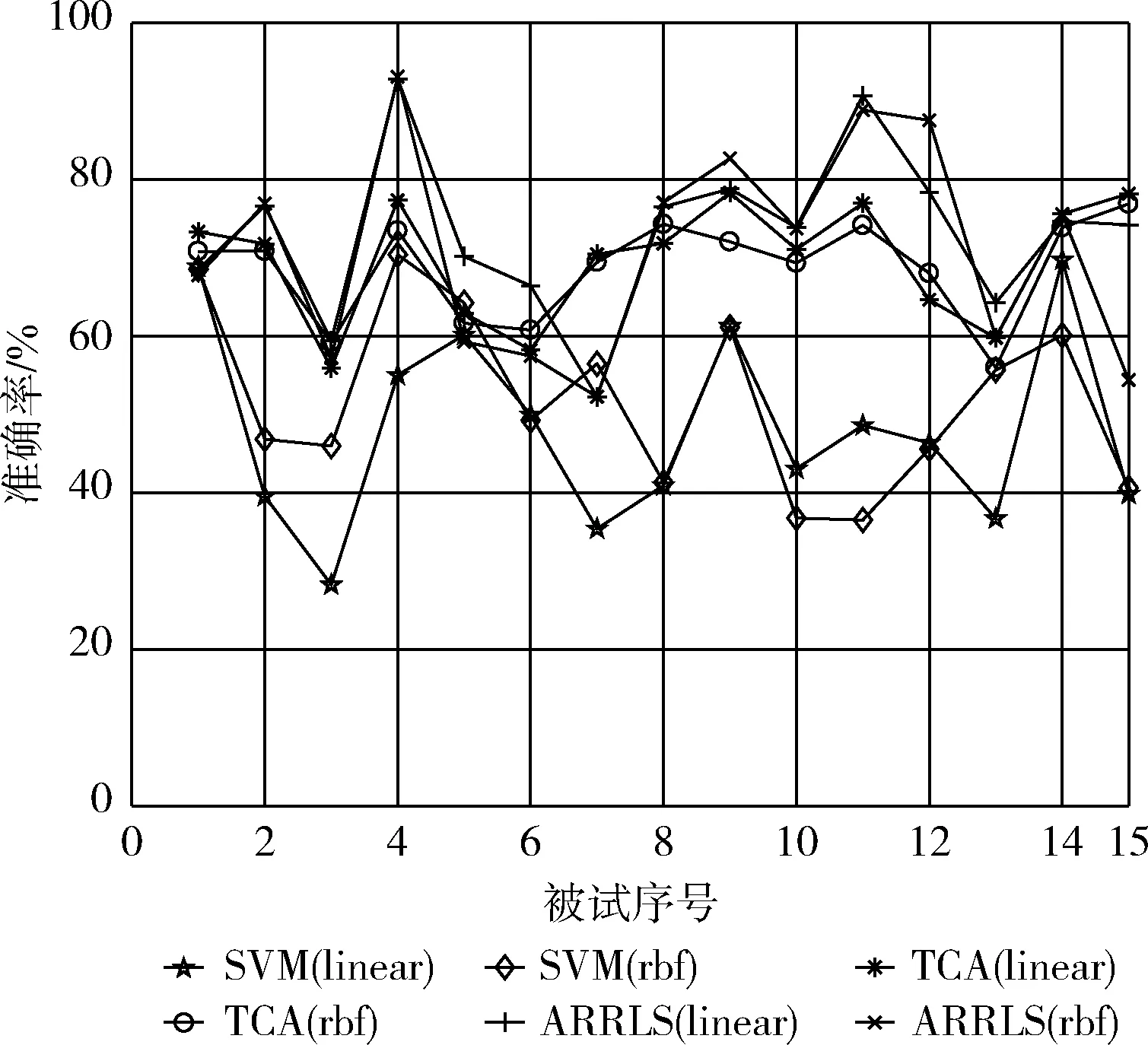
图5 单个个体识别准确率
此外,通过图6可以看出同一目标域对应的不同源域在使用ARRLS算法时分类结果相差较大。图5中分别选取被试1,2作为目标域。当被试1作为目标域时,被试2,3,12作为源域时识别精度较低。当被试2作为目标域时,被试3,12作为源域时识别精度较低。当存在部分识别率较低的源域被试时,若直接对所有源域的识别结果投票将会导致最终模型识别率变低。针对上述存在的两个不足,本文进一步提出结合样本选择和特征选择的多源域迁移学习算法。
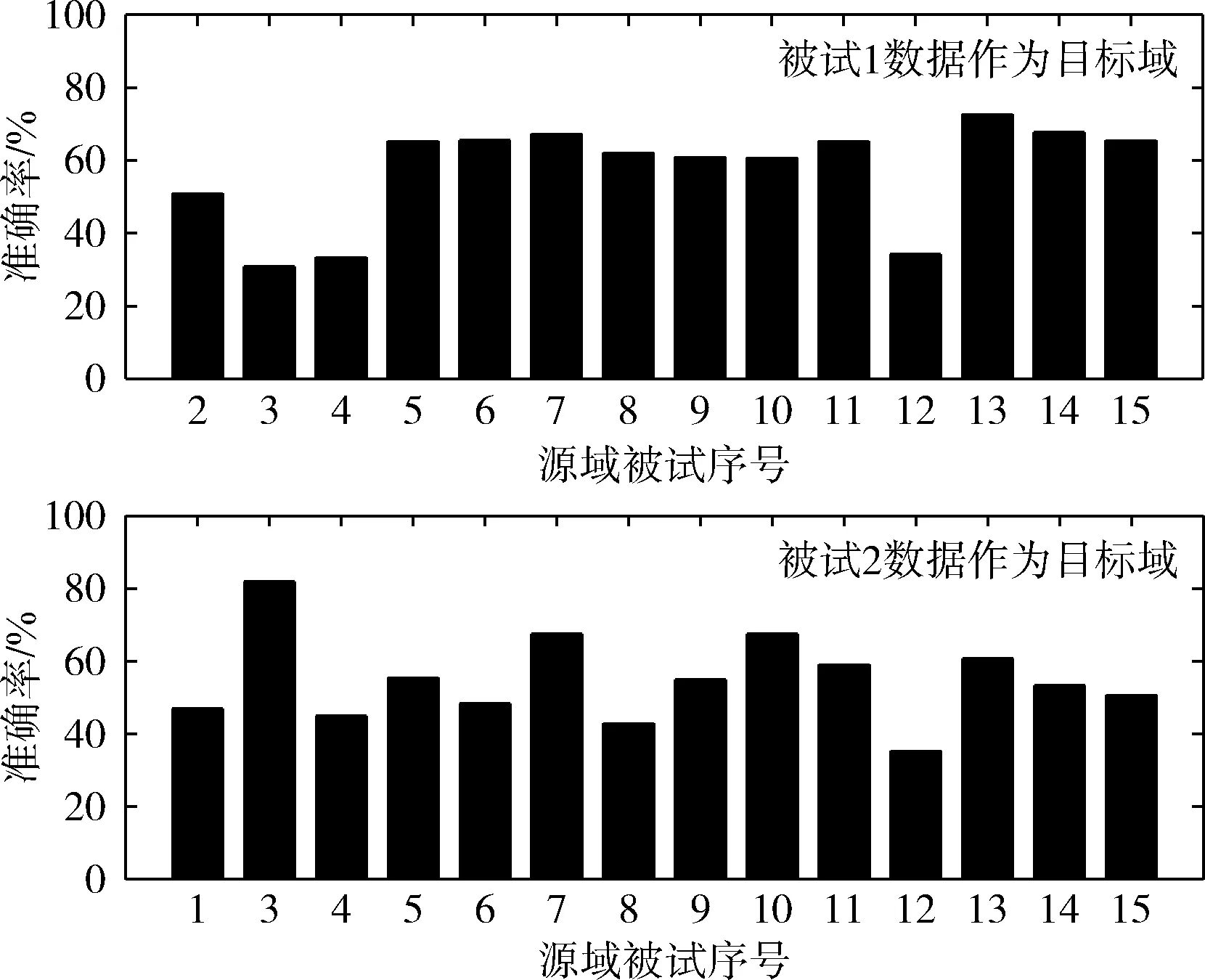
图6 被试1,2作为目标域时不同源域的分类结果
3.3 MDS算法性能分析
为了提升识别效率同时提升模型性能,本文通过MDS算法衡量出源域与目标域间相似性的大小,保留具有良好迁移能力的源域。图7是一名被试作为目标域,在K=2,3,5时14个源域被试根据相似性大小进行聚类的示意图。

图7 MDS算法实验结果
被试间相似度大小可以由图中每名被试的对应点到原点的距离直观看出,距离原点越远则相似性越高。从图6中可以得出,不同源域被试与目标域被试间的MMD值和Like值差异较大。K-means算法根据联合相似度的大小将原始源域集合聚类,不同的K值得到的聚类结果也不相同,本文选取距离零点距离较远的集合作为最优子集来避免出现负迁移现象。当K=2时,保留形心模值较大的集合中所包含源域,此时聚类效果较为极端,所选取的最优源域集合仅包含1名被试数据。当K=3时,保留形心模值最大的2类包含的源域,此时最优源域集合有8名被试组成。当K=5时,保留形心模值最大的3类包含的源域,此时聚类结果适中,最优源域集共有5名被试数据集组成。
3.4 TFS算法性能分析
由于原始数据中存在部分与标签无关且影响迁移效果的特征,因此本文采用TFS算法去除这些特征。TFS算法首先计算出所有特征权重值F(fi),并根据权重值对所有特征排序。式(12)为当维度为d时的特征权重占比率rate的计算公式,其中Z为特征总体维度,F(fi)为特征fi的Fisher Score大小
(12)
本文考虑到数据信息的完整性与计算成本控制,选取占比率为0.85时所对应的最优子集SF,特征维度d=100。对SF中的所有特征计算互信息I(fi)大小,并将由小到大排序,选取最终特征子集SI。图8为Fisher Score与TFS算法在不同维度下的实验结果图。
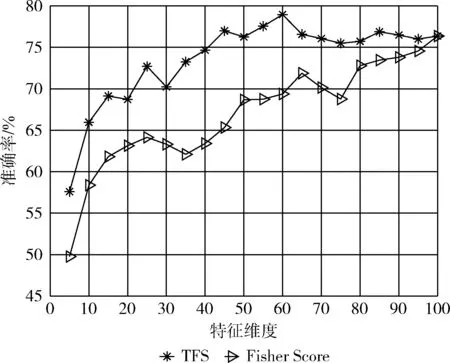
图8 特征选择实验结果
从图8中可以看出,利用Fisher Score与TFS算法实验精度在初始阶段会随着所选特征数量的增加而提高,且TFS识别效果明显优于Fisher Score,这说明TFS算法成功选出对迁移有效的特征并排在特征序列的前列。但TFS算法所选特征维度达到一定维度后,其精度逐渐开始下降,这说明随着后续与域标签强相关的特征加入集合中,源域与目标域间的差异性也随之增加,影响迁移效果,从而降低识别精度。
3.5 MDS-TFS-ARRLS算法性能分析
为了最大限度提升计算效率和分类效果,本文将MDS、TFS和ARRLS算法相结合进行实验,并将之与其它组合方式做出对比。ARRLS、TFS-ARRLS、MDS-ARRLS和MDS-TFS-ARRLS分别对应迁移学习,特征选择+迁移学习,多源域选择+迁移学习,多源域选择+特征选择+迁移学习4种情况,这4种方式在linear核情况下的实验结果见表2。
从表2中可以看出,仅使用ARRLS算法可以得到73.19%的准确率,但所用的时间为1442 s,计算效率过低。TFS-ARRLS算法对所有源域进行特征选择,在60维下分类,从表中可以看出由于去除冗余特征即降低特征维度,使计算时间在一定程度上有所减少,减至703 s,同时准确率也提高至78.96%。MDS-ARRLS算法为使用多源域选择后再分类,随着K值的不同对应的样本保留率也不同。当K=2时,选取的样本为原始的35%,所得准确率略微低于原始准确率。当K=3或5时,所选样本数量相对增加,其对应的准确率都高于原始值,并且可以看出3种K值的计算时间都大幅缩减。MDS-TFS-ARRLS算法中,同时兼顾了特征选择和样本选择两个方面,进一步提升识别效率与识别率。当K=2时,虽然计算时间最短,但由于去除了过多样本信息,相较于TFS-ARRLS,计算准确率降低了1.39%。K=3时,对应准确率为79.92%,相较于原始准确率提高6.73%,计算效率提高3.84倍。K=5时,兼顾了分类准确率和计算效率两个方面,其分类准确率提高6.35%同时计算效率提高5.02倍。

表2 4种迁移学习算法实验结果
从表3中给出当K=3时,MDS-TFS-ARRLS在不同维度下的识别精度与计算时间的变化情况,当保留较多特征时,其计算精度相对较高,但其计算成本同时也随之提高。在实际应用中可以根据实际所需选取合适的特征集合大小。
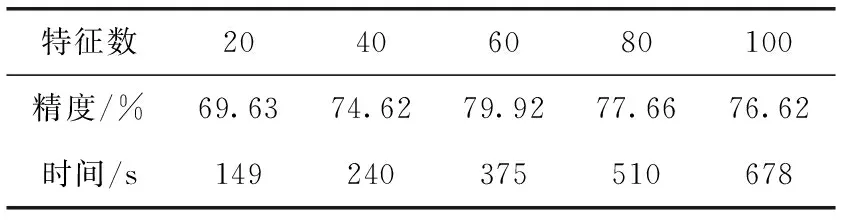
表3 MDS-TFS-ARRLS算法最终选取不同维度结果
综合上述实验结果,本文所提出的MDS-TFS-ARRLS算法可以有效提高计算效率且提高分类准确率。
3.6 同类结果对比
将本文提出的方法与同样采用SEED数据集的其它方法的实验结果作对比,见表4。文献[19]使用深度信念网络(deep belief network,DBN)选取最优电极组合,得到67.84%的分类精度;文献[20]从脑电信号中提取18种线性和非线性脑电特征,并从中自动选取与情感最相关的特征信息,利用支持向量机达到83.33%的识别率。这两篇同类研究分别利用深度学习和浅层机器学习算法建立模型,但都没有应用迁移学习从本质上减小源域与目标域间数据分布差异。文献[21]中采用辨别图正则化极限学习机(GELM)来识别随时间变化的稳定模式,该文研究同一个被试跨天情感识别,因此训练集与测试集差异小于本文,最终分类精度为79.28%。文献[22]使用最大独立性领域自适应算法(maximum independence domain adaptation,MIDA),以差分熵作为特征取得72.31%的分类精度;文献[23]使用TCA迁移学习方法,但训练集设置为随机取出的5000个样本,通过将数据降至30维取得69.44%的精度。上述两篇文献虽然都采用了迁移学习算法,但相较于本文,并未考虑多源域选择算法去除会引起负迁移的源域。
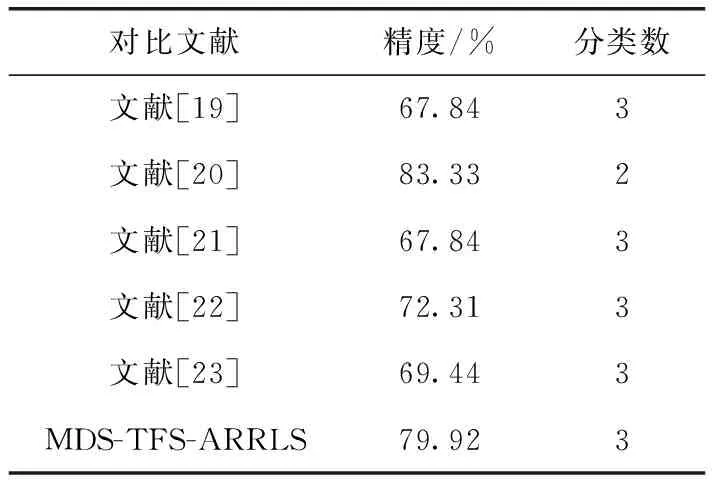
表4 同类研究对比
4 结束语
本文提出一种将多源域选择(MDS)、迁移特征选择(TFS)和适配正则化线性回归(ARRLS)结合建立模型的方法,并将其应用到跨被试情感识别中。该模型考虑到目标域与源域间相关性,用多源域选择来合理选择样本信息;其次考虑到特征自身与类别标签和域标签间的相关性,使用迁移特征选择算法去除冗余特征;最后对多个迁移学习分类模型集成。结果表明,本文算法可以去除数据集中的无关样本与特征,具有良好的计算效率,该算法相比于其它方法具有更优的跨被试情感识别能力。

