SIR粒子滤波的改进算法
孔红山,李小鹏,郁 滨
(信息工程大学 密码工程学院,河南 郑州 450001)
0 引 言
粒子滤波(particle filter,PF)不仅能处理噪声服从高斯分布的线性系统,而且可以处理非高斯噪声的非线性系统[1-3]。序贯重要性重采样(sequential importance resampling,SIR)粒子滤波算法,通过在粒子滤波算法中加入重采样环节解决粒子退化问题,但也带来了粒子贫化问题。
为了解决SIR-PF算法的粒子贫化问题,很多学者进行了改进重采样环节的相关研究。文献[4]提出了一种基于分类重采样的改进粒子滤波算法;文献[5]提出了利用邻域搜索重采样改进粒子滤波算法,提高了粒子多样性,但并没有解决粒子贫化的问题。在基于重采样的粒子滤波框架下进行算法改进,不能从本质上解决粒子贫化问题,很多学者从交叉学科与粒子滤波相融合的角度进行了研究。文献[6-8]分别提出了基于遗传算法、鸽群算法和萤火虫算法的粒子重采样算法,大大提高了粒子有效性和多样性。通过引入人工智能优化算法与粒子滤波相结合,是一种更加有效解决粒子贫化问题的思路。
粒子群优化算法是一种有效的全局寻优算法,文献[9]提出基于高斯粒子群优化算法的粒子滤波改进方法,高斯粒子群优化算法没有惯性项,简化了优化计算过程,但也降低了全局搜索能力;文献[10]提出基于标准粒子群优化算法的粒子滤波改进算法,但标准粒子群优化算法容易陷入局部收敛。本文引入动态调整惯性系数和变异算子对粒子群优化算法进行改进搜索过程,提高算法的全局收敛速度、粒子多样性,且避免陷入局部收敛,并在SIR-PF算法框架的基础上,利用改进的粒子群优化算法对序贯重要性采样后的粒子集进行优化,采用优化后的粒子集进行状态变量估计,本文所提算法称为基于改进粒子群优化的粒子滤波算法(IPSO-PF)。
1 IPSO-PF算法
1.1 基本思想
SIR-PF算法存在粒子贫化问题的根源是重采样环节。重采样使得高权重粒子被多次复制,低权重粒子被直接舍弃,造成重采样后的粒子由大量重复的点构成,带来粒子贫化问题。为了解决粒子退化问题加入了粒子重采样环节,取消重采样环节就会导致计算资源的浪费和估计结果的偏差。重采样实际上是为了解决粒子的低效问题,而粒子数量又不能无限制的增加。引入粒子群优化算法对序贯重要性采样后的粒子分布进行优化,使得粒子集更加趋于向高似然区域移动,提高粒子集中每个粒子的效用,又无需增加粒子数量,解决了粒子退化问题。同时,在粒子群优化过程中,一是只存在粒子位置的变化,并且每个粒子位置变化是随机的,二是每个粒子均得到了保留,有效解决了粒子贫化问题。总结起来,通过粒子群对粒子分布的优化既可以替代重采样环节的作用,解决粒子退化问题,也可以解决粒子的贫化问题。IPSO-PF算法包括序贯重要性采样、粒子群优化过程和状态估计3个环节。
1.2 改进的粒子群优化算法
假设在D空间中,随机初始化一个粒子数为N的粒子种群N={p1,p2,…,pN}, 设第i个粒子的位置和速度分别为pxi=(xi1,xi2,…,xiD)T和pvi=(vi1,vi2,…,viD)T。 种群的个体极值表示为pbi=(pbi1,pbi2,…,pbiD)T, 全局极值表示为gb=(gb1,gb2,…,gbD)T, 粒子按照下式更新速度与位置
(1)
(2)
其中,r() 为(0,1)之间的随机数;c1和c2为加速常数,分别代表粒子向个体极值和全局极值移动的权重;w为惯性系数,w较大表示全局搜索能力强,w较小表示局部搜索能力强。
为了改进搜索过程,提出一种动态调整惯性系数的方法,使得搜索过程中惯性系数线性递减。假设搜索的迭代次数为Maxgen,w的最大值为w_max,w的最小值为w_min, 那么迭代第ii次的惯性系数为
(3)
为了提高粒子多样性和搜索速度,借鉴遗传算法的变异思想,引入变异算子,每隔一定的周期L, 粒子状态和速度按下式进行一次更新
(4)
(5)
其中,randperm(n) 为产生一个[1,n]之间的整数数列。
1.3 适应度函数
通过计算粒子集中每个粒子的适应度值,把适应度值最大的粒子认定为最优粒子,粒子群优化算法驱使粒子向最优粒子移动。优化过程使得那些远离真实状态的粒子趋向于真实状态出现概率较大的区域,进而达到粒子分布优化的目的。
定义粒子群优化算法中粒子的适应度函数为
(6)
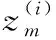
1.4 粒子分布优化过程

步骤2 利用式(6)计算每个粒子的适应度值,并作为粒子局部极值;计算粒子集中的最优适应度值,作为粒子全局极值;
步骤3 判断迭代次数是否能整除L, 若是,利用式(4)、式(5)更新粒子状态和速度;若否,由式(3)得到惯性系数,由式(1)、式(2)得到粒子集迭代后的粒子状态和速度。
步骤4 由式(6)计算当前粒子集的适应度值,依据适应度值更新局部极值和全局极值。
步骤5 判断迭代次数变量是否小于等于迭代次数Maxgen, 若是,迭代次数变量加1转至步骤3;若否,粒子分布优化过程结束,把当前的粒子集送至算法下一环节处理。
1.5 算法流程
IPSO-PF算法完整的流程见表1。
2 仿真实验及分析
为了衡量IPSO-PF算法的滤波性能,采取典型的非线性系统进行数值仿真实现,并与SIR-PF、PSO-PF、GPSO-PF这3种算法从滤波精度、粒子退化、粒子贫化和运行时间4个方面进行性能比较。

表1 IPSO-PF算法
该系统的过程方程和观测方程分别为
xk=1+sin(0.04*π*k)+0.5xk-1+ωk
(7)
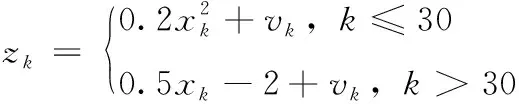
(8)
式中:ωk、vk分别为系统噪声和观测噪声。
2.1 滤波精度
假设系统初始状态x0=0.1, 系统噪声为服从伽马分布Γ(3,2) 噪声,观测噪声方差为1的零均值高斯噪声,粒子个数为50,仿真时间步数为60,采用IPSO-PF、SIR-PF、PSO-PF和GPSO-PF这4种算法对非线性系统滤波的仿真,其中IPSO-PF、PSO-PF和GPSO-PF这3种算法的加速常数和迭代次数相同,取值分别为c1=c2=2、Maxgen=20, IPSO-PF算法中惯性系数取值为w_max=0.9、w_min=0.4、L=4, PSO-PF算法中惯性系数取值为w=1.0, 4种算法的滤波估计值和误差如图1所示。
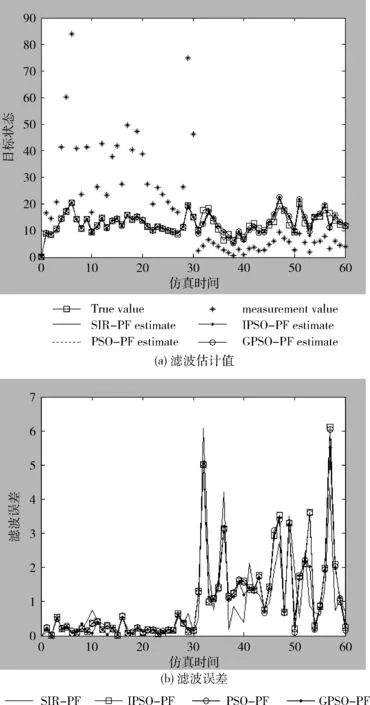
图1 滤波估计值及误差
从图1(a)可知,4种算法在系统存在较大的非高斯噪声条件下均能达到较好的滤波效果;从图1(b)可知,SIR-PF算法的最大误差约为6.08,PSO-PF算法的最大误差约为6.06,GPSO-PF算法的最大误差约为5.53,IPSO-PF算法的最大误差约为5.50,SIR-PF算法的平均误差约为0.96,PSO-PF算法的平均误差约为1.03,GPSO-PF算法的平均误差约为0.98,IPSO-PF算法的平均误差约为0.92,与其它3种算法相比,IPSO-PF算法滤波精度稍优。
为了比较不同算法滤波精度,引入均方根误差RMSE作为评价指标,其数学表达式为
(9)
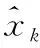
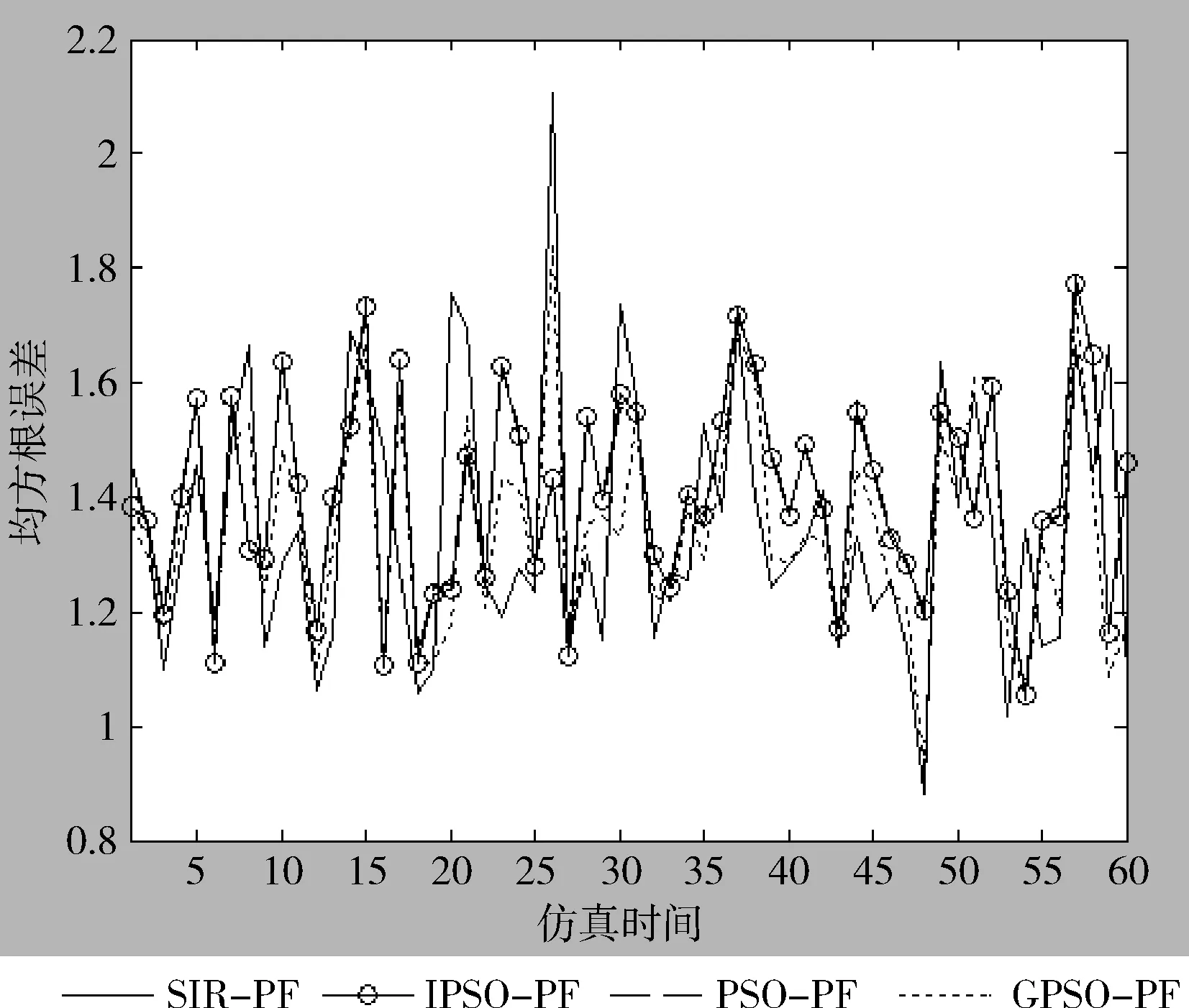
图2 均方根误差
由图2可知,SIR-PF算法的RMSE均值约为1.34,PSO-PF算法的RMSE均值约为1.40,GPSO-PF算法的RMSE均值约为1.34,IPSO-PF算法的RMSE均值约为1.33,4种算法滤波精度基本相同;SIR-PF算法的RMSE方差约为0.32,PSO-PF算法的RMSE方差约为0.21,GPSO-PF算法的RMSE方差约为0.19,IPSO-PF算法的RMSE方差约为0.17。与SIR-PF算法相比,3种粒子群算法稳定性都得到大幅提高,而IPSO-PF算法稳定性优于另外两种粒子群算法。
2.2 粒子退化
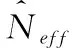
(10)
仿真参数不变,采用IPSO-PF、SIR-PF、PSO-PF和GPSO-PF这4种算法对非线性系统进行一次滤波仿真,有效粒子数曲线如图3所示。
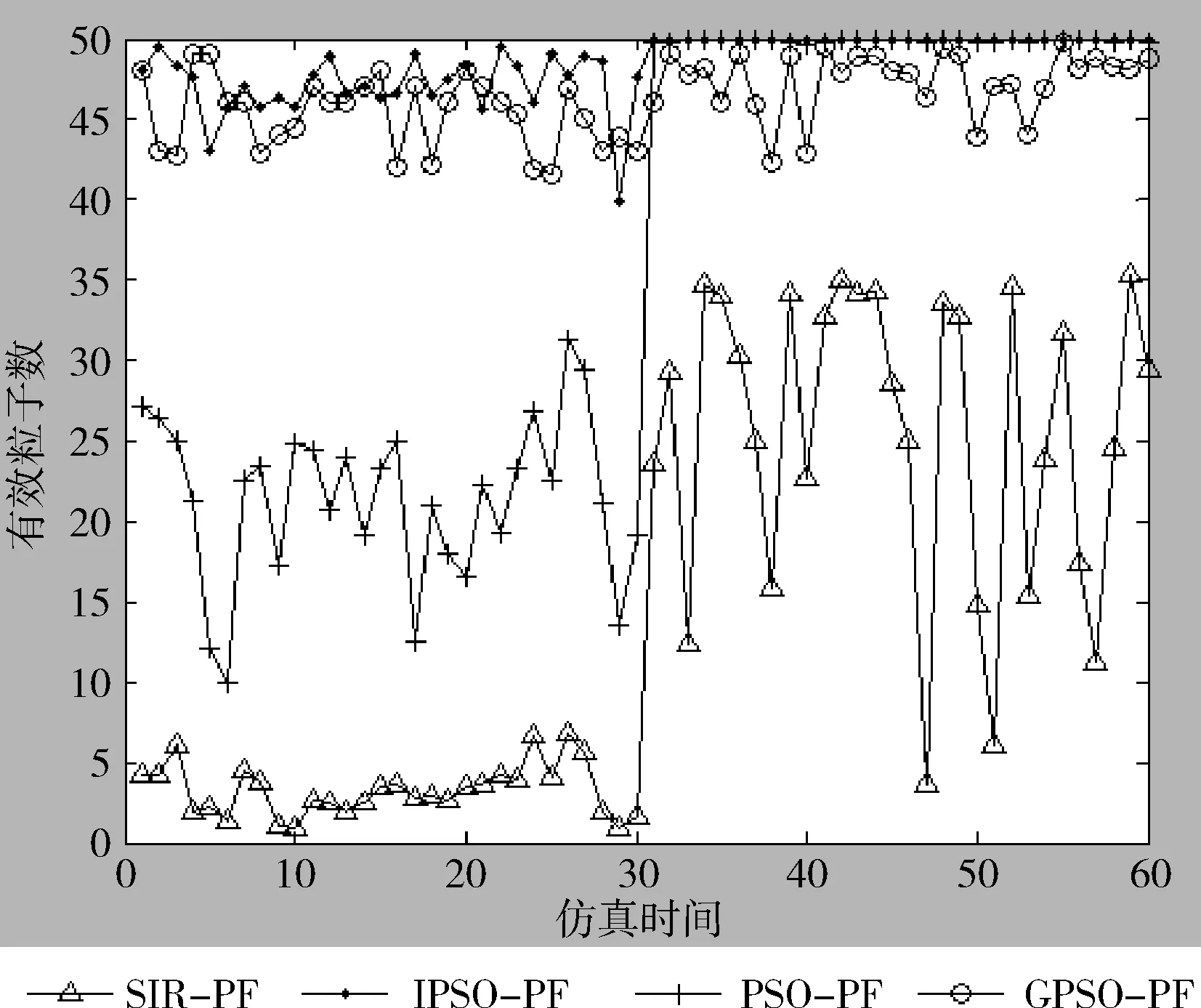
图3 有效粒子数
由图3可知,SIR-PF算法的有效粒子数的平均值约为14.4,PSO-PF算法的有效粒子数的平均值为35.7,GPSO-PF算法的有效粒子数的平均值为46.3,而IPSO-PF算法的有效粒子数的平均值为48.6。可以表明,对重要性采样后的粒子,通过粒子群优化算法进行粒子分布优化来代替重采样环节,可以使滤波的有效粒子大大增加,是一种粒子解决粒子退化的有效办法,与PSO-PF和GPSO-PF两种算法相比,IPSO-PF算法的有效粒子数的平均值更大。
2.3 粒子贫化
仿真参数不变,采用IPSO-PF、SIR-PF、PSO-PF和GPSO-PF这4种算法对非线性系统滤波进行一次仿真,取粒子在k为11和12两个时刻的粒子真实值、IPSO-PF粒子状态值、SIR-PF粒子状态值、PSO-PF粒子状态值和GPSO-PF粒子状态值的分布情况,如图4所示。

图4 两种算法的粒子状态分布
由图4可知,SIR-PF算法的粒子分布往往集中在少数几个高权重状态值上,粒子重复率高,降低了粒子的多样性,不利于滤波的状态估计。IPSO-PF、PSO-PF和GPSO-PF这3种算法粒子呈现出绝大部分粒子集中于真实值附近且粒子分布相对均匀,除此之外,仍然合理保留了少数低权重粒子,确保了粒子多样性。与PSO-PF和GPSO-PF两种算法相比,IPSO-PF算法在保证多样性的同时,粒子更加集中于真实值附近。
2.4 运行时间
在32位windows7操作系统、Intel酷睿i7-4500U处理器环境下,设置粒子个数分别为30、50、100、500,其它参数仿真保持不变,在MATLAB仿真运行4种算法,运行时间见表2。
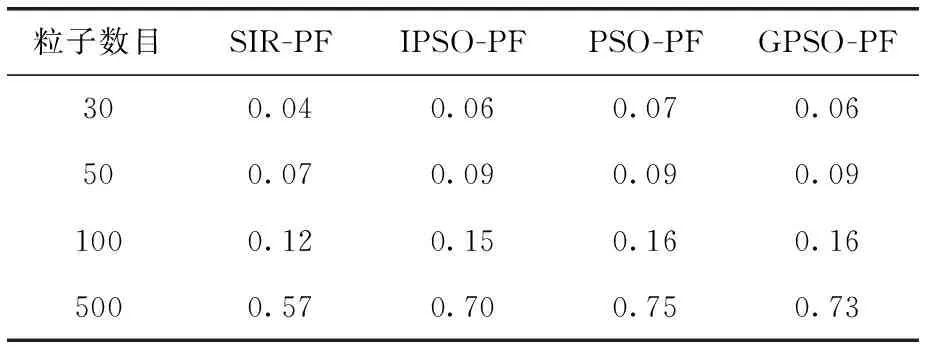
表2 运行时间
由表2可知,在不同粒子数目下,IPSO-PF、PSO-PF和GPSO-PF算法的运行时间基本相同,且都大于SIR-PF算法,这是由于粒子群优化过程代替重采样过程,表明粒子群优化过程的复杂度大于传统的重采样过程;IPSO-PF算法需要的粒子数量较小,这种情况下,IPSO-PF算法的运行时间与SIR-PF算法相差不大,也能很好满足滤波的实时性要求。
2.5 搜索过程
为了衡量IPSO-PF算法的搜索性能,仿真参数保持不变,抽取k=1时刻的序贯重要性采样后的粒子集,采用IPSO-PF、PSO-PF和GPSO-PF这3种算法进行粒子分布优化的适应函数值变化曲线如图5所示。
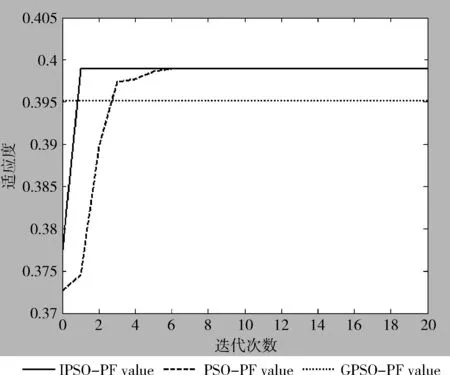
图5 适应函数值变化曲线
由图5可知,GPSO-PF算法收敛于局部最优值0.3951,并且没有改变,这是由于算法省略了惯性项,降低了全局搜索能力,易陷于局部最优;PSO-PF算法在经过一段时间后收敛于0.3989,算法具有较强的全局搜索能力,但收敛速度较慢,并且搜索过程后期由于粒子速度变慢也可能陷于局部最优;IPSO-PF收敛速度较快,且具有较好的全局寻优能力,这是由于引入动态调整惯性系数和变异算子对粒子群优化算法进行改进,提高了算法在搜索性能。
3 结束语
为解决SIR粒子滤波算法存在的粒子贫化问题,提出了基于粒子群优化的SIR粒子滤波改进算法IPSO-PF。与SIR-PF、PSO-PF、GPSO-PF这3种滤波算法相比,IPSO-PF算法滤波精度稍优,且滤波稳定度更好;在滤波过程中的有效粒子数的平均值更大,粒子退化问题也得到较好的解决;粒子大部分集中于高似然区域,但保留了少数低似然区粒子,并且粒子更加集中于真实值附近;运行时间大于SIR-PF算法,但也能满足实时性要求;收敛速度较快,且具有较好的全局寻优能力。总体来讲,IPSO-PF算法在增加部分运算量的前提下,取得比SIR-PF、PSO-PF、GPSO-PF这3种算法更好的综合滤波性能。下一步的研究重点是在IPSO-PF算法的基础上进行优化,进一步提高滤波精度和稳定性,并降低其运算复杂度。

