基于ANSYS-Workbench的自动化立体仓库重型堆垛机货叉力学分析

董先瑞，孟 岳，滕晨晨，楚新新

（1.聊城轩宇信息技术有限公司，山东 聊城 252000；2.聊城水城慧德学校，山东 聊城 252000）

1 引言

随着现代企业生产经营方式的变革和市场外部条件的变化，以降低原材料成本和进行产品技术开发来降低产品成本的空间越来越小，并且随着国家对土地资源监控越来越严，土地成本也在急剧增加，这使得企业把目光转向物流环节，自动化立体仓库由此产生。自动化立体仓库能够利用更小的空间，实现更多的库存量，增加库存量；减轻劳动强度；减少货物破损率；实现快速整盘出入库、拣选、配送作业，整个系统运行效率比普通仓库提高100-500%；采用计算机进行控制管理而利于企业实施现代化管理。随着科学技术的发展进步，自动化仓库技术将进一步向系统化、网络化、无人化方向发展，自动化立体仓库在企业的广泛应用将为进一步提高企业的综合经济效益发挥重要的作用[1-6]。

堆垛机是自动化立体仓库中最关键的起重搬运设备。堆垛机主要在高层货架内从巷道口出入库平台到货位之间穿梭，实现货物的取、搬运、放动作。堆垛机主要由底梁、行走机构、立柱、升降机构、顶梁、载货台及货叉组成，如图1所示。货叉是堆垛机取放物料的伸缩机构，是堆垛机的核心机构。为了尽可能提升货架存储率，使货物在货架上摆放整齐、存取货物灵活可靠、降低设备自重等，设计货叉时在满足强度的情况下还需满足降低自身高度，结构紧凑、重量轻、满载挠度小、稳定性高等条件。因此货叉是自动化立体仓库堆垛机设计中难度较大的机构。本文针对货叉在存取货物时出现冲击振动大，存取货定位不准、运行不太稳定等现象，对货叉进行了优化，并利用理论数学模型和ANSYS-Workbench软件对研制出的样机进行受力和模态测试，样机通过测试后应用在东阿钢球集团有限公司立体仓库的实际工作中，并在实际工况中对其进行测试，证明其满足性能需求。

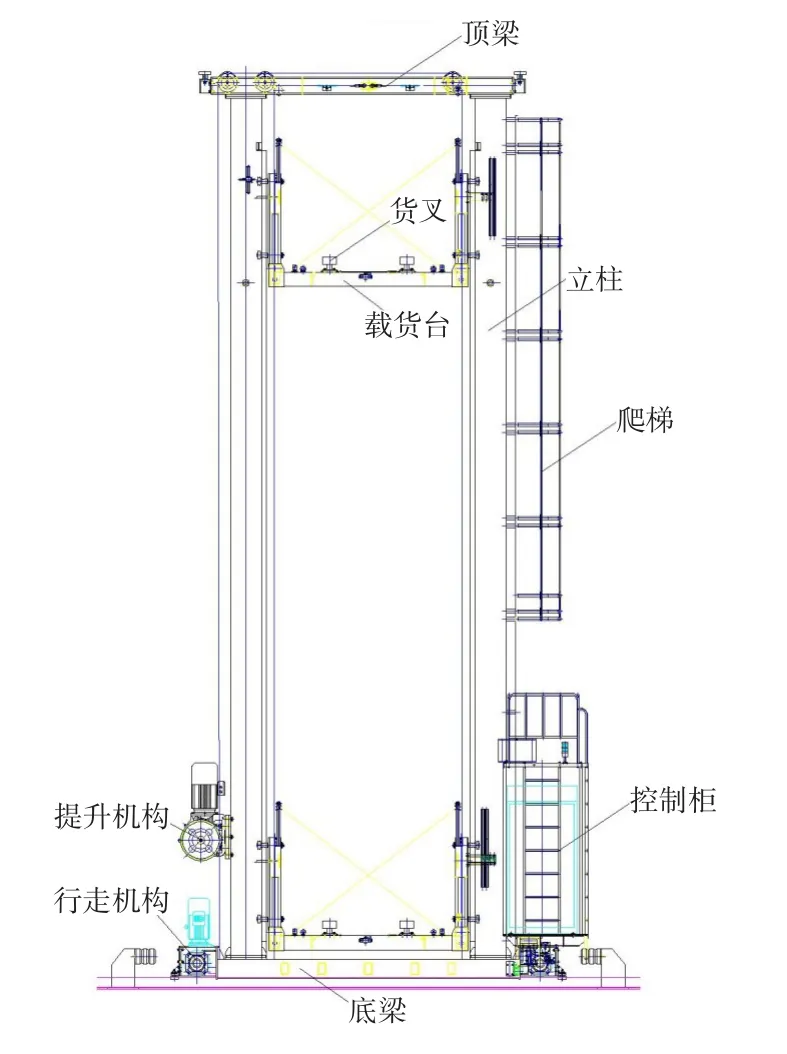
图1 堆垛机模型

2 工作原理

货叉分为单伸货叉和双伸货叉，单伸货叉由上、中、下叉和动力驱动机构组成，双伸货叉由上、中上、中下、下和动力驱动机构组成。货叉采用三级直线差动式结构原理驱动，动力驱动带动货叉有齿轮齿条、链轮链条、同步轮同步带等几种方式，根据货叉载重、空间机构及成本等多因素进行选择。本文以运载1210型标准托盘，载重为1t的货叉为对象，货叉下叉通过固定座与载货台固定，两组链条穿过主动链轮、中叉上的从动链轮把下、中、上连接起来，实现倍增机构，电机经链条带动主动链轮，货叉的上叉可以左右伸出、伸回，经过载货台升降动作的配合实现货位产品的取放。货叉之间的支撑机构是货叉的关键，本研究中，优化后的下叉与中叉之间的支撑轴承和中叉与上叉之间的支撑轴承根据运行距离合理布置10组支撑点，保证货叉伸出后10组支撑点同时承受最优支撑力。货叉的结构如图2所示。

图2 货叉模型

3 力学模型的建立

货叉是经常在满载和空载情况下启动、制动的机械机构，在运动过程中，货叉的伸出、缩回的速度、加速度和加速度的变化率都是在变化的。当货叉在运动过程中，货叉及产品的重量、导向支撑系统支撑点的变化、各种检测开关碰撞接触、电机产出的扭力载荷、两组链轮链条啮合间隙及制造过程的误差等因素使货叉之间存有激振从而产生动力载荷。货叉在工作过程中受力比较复杂，所以建立货叉的力学模型进行力学分析。

当货叉满载产品伸出时，货叉的受力最大，挠度变形最大，严重时出现产品下滑现象，需要对货叉的下挠度进行校核，将货叉进行适当的简化，货叉受力最大的模型如图3所示，建立货叉的挠度近似微分方程如下：

图3 货叉受力挠度模型示意图

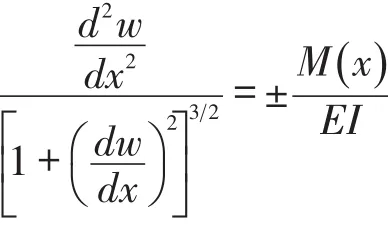
根据货叉受力模型解得货叉最大挠度量为：

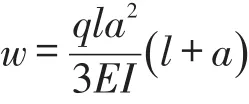
式中：叉体宽度175mm，叉体高度65mm，叉体长度l=1 200mm，上叉完全伸出，上叉中心离下叉距离a=700mm，两组货叉承受载荷为1 000kg，E为弹性模量，I为惯性矩，带入数据得出叉体变形挠度为：w=12mm。

货叉系统中，当货叉伸出和缩回时，由于频繁开闭电机会产生力矩冲击的动力载荷；货叉伸缩采用齿轮齿条驱动，由于齿轮、齿条的跳动，啮合间隙及制造的误差使机构激振而产生动力载荷；同时，与行程开关碰撞接触都会引起振动和冲击，都会产生动力载荷。模态分析可以用来确定结构的自振频率和相应振型，为结构设计提供依据，避免在动力载荷作用下发生共振现象，提高结构系统的振动性能。因此,根据有限元方法建立货叉的振动基本方程：

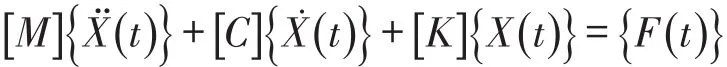
研究货叉的动力学问题，很重要的一部分是计算货叉结构的固有频率和固有振型，它是分析结构动力响应和其它动力学特性问题的基础。将货叉的振动基本方程进行求解得出

结构的刚度矩阵[K]和质量矩阵[M]均为n阶方阵，n是节点自由度数，求出结构的n阶固有频率，{X}是对应n阶固有频率的结构振型。

4 基于ANSYS-Workbench的有限元分析

货叉满载加减速伸缩货叉过程中的受力情况是比较复杂的，为了进一步了解货叉所受应力、变形的分布情况，利用计算机ANSYS-Workbench软件对货叉做有限元仿真分析。这里以货叉满载受力、货叉伸出状态为分析对象。

为了提高分析效率，并且使有限元模型尽可能反映工程实际情况，对货叉模型进行了简化。动力装置、链轮链条传动机构仅仅起到动力传动作用，不存在支撑受力情况，所以在简化时将其去掉了，货叉中下叉与中叉之间支撑轴承和中叉与上叉之间支撑轴承根据运行距离合理布置的10组支撑点及螺栓连接部分通过布尔运算给连在了一起。同时从货叉的工作情况可以知道，货叉在满载并且伸叉到极限取货时刚度最差，相应产生的挠度就最大。在简化模型时把货叉停留在伸叉取货到极限的情况，将模型导入ANSYS-Workbench软件中进行分析。

货叉采用45号钢，材料密度为7.86×10-6kg/mm3，材料的弹性模量E=206GPa，剪切模量560MPa，泊松比μ=0.25，屈服极限为1 170MPa。采用六面体域网格划分方式对货叉进行网格划分，划分完成后，对货叉的4个安装板施加固定约束条件，对上叉施加1t的载荷，然后进行求解。得出货叉变形云图和应力云图，如图4-图7所示。

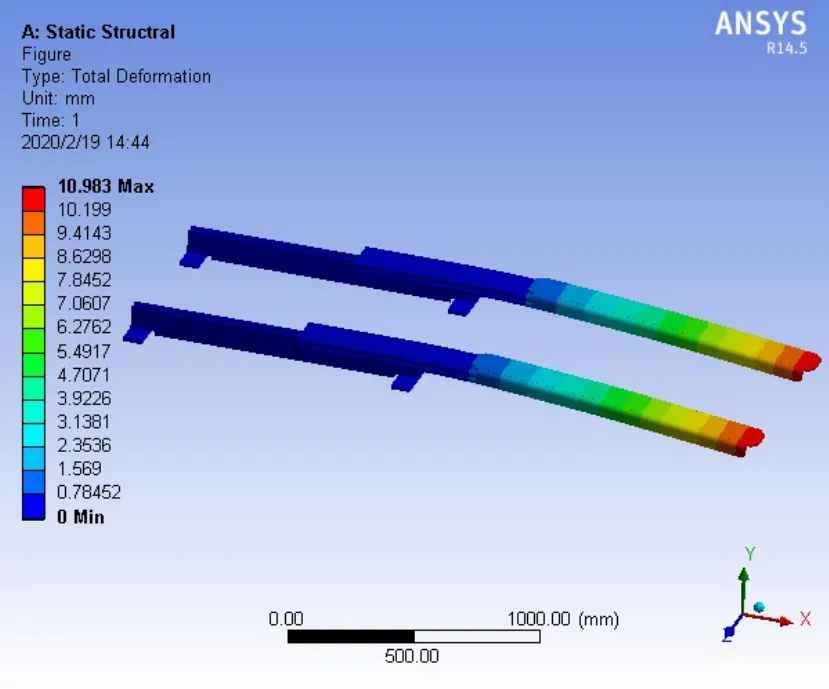
图4 货叉的总变形云图

图5 货叉的Y方向变形云图

从图4、图5可知，货叉之间支撑点全部受力，承受1t的载荷时货叉在受总变形为11mm，主要变形在Y方向，与理论力学模型计算相符；货叉的变形量减小，有明显改善。

从图6、图7可知，货叉之间支撑点全部受力，承受1t的载荷时货叉主应力集中在上叉与中叉之间靠近中叉端侧的支撑点，受力为188MPa，货叉最大应力集中在中叉与下叉之间靠近下叉端侧的支撑点，受力为162MPa，均满足载荷要求。

图6货叉的主应力云图

图7货叉的最大应力云图

货叉的振动特性影响货物的稳定性，货叉模态分析可以使我们了解货叉的固有频率，认识货叉结构对于不同类型的动力载荷是如何响应的。根据优化后模型生产、组装货叉，生产产品如图8所示。货叉样机在载满核定载荷伸出后，货叉挠度变形为10mm，与计算、仿真分析结果匹配。对优化前和优化后的模型进行模态分析，得出固有频率见表1。

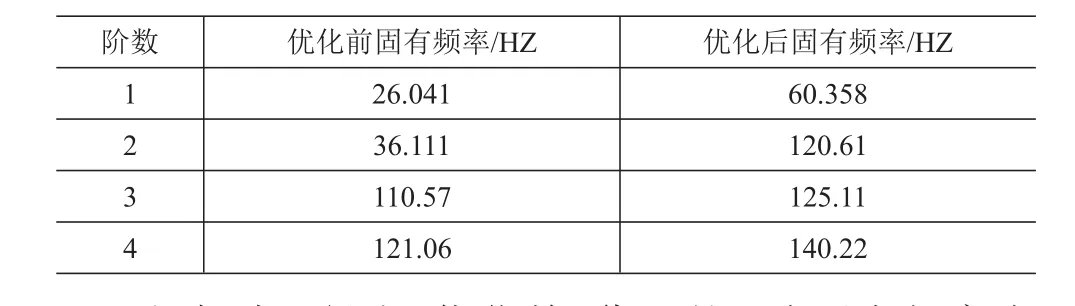
表1 货叉的固有频率

根据表1得出，优化前，货叉的1阶固有频率为26.041Hz，货叉运行中很容易发生共振现象，影响货叉的稳定性。优化后，1阶固有频率是60.358Hz，货叉共振频率提高，货叉的稳定性得到提升。

图8 优化后货叉

5 结论

巷道堆垛机是智能立体仓库的主要设备，货叉是堆垛机的关键工作装置，由于结构布局、货叉长度小于巷道宽度、工作行程大于本身长度等因素，导致货叉在存取货物时发生冲击和振动，从而引起产品精度、稳定性方面的问题。本文对货叉进行了优化，并通过系统结构数学模型和ANSYS-Workbench软件进行计算和仿真分析，证明货叉工作中受力满足载荷要求。根据优化后模型生产样机，对样机进行受力和模态测试，受力后挠度变形与仿真结果匹配，降低了挠度变形量，样机通过测试后应用在东阿钢球集团有限公司立体仓库中，对实际产品进行模态测试，证明优化后的货叉提升了货叉系统的固有频率。