齿轮箱振动检测及不同转速齿轮应力分析

管柯鸣，高元涛

（浙江鼎盛石化工程有限公司，浙江舟山 316000）

0 引言

某企业氢气压缩机由汽轮机通过齿轮箱减速后带动螺杆压缩机，在一次试车中，按正常启机流程启机，前期设备各振动温度均正常，直至转速升至10 500 r/min，再往上升速的过程中，DCS（Distributed Control System，分布式控制系统）检测到齿轮箱振动直线上升，直至振幅超过报警值跳车。

根据以往经验，第一反应是齿轮箱出现机械方面的干涉或磨损导致振动大，遂即在机组正常停机后，对齿轮箱进行解体检查，发现各尺寸配合均在标准之内，接触面无磨损痕迹，油质分析、仪表信号也无异常。

在确认机械方面无任何问题后，对振动信号进行分析，频谱显示多为1×幅值上升，怀疑是共振引起的振动增大。

为验证这一猜想，决定再次试车。前期流程一样，直至转速提升至10 000 r/min 后，运行20 min，检测振动温度稳定无异常，随后以100 r/次逐级提升转速，同时监测振动幅值。在转速提升至10 500 r/min 时，振幅出现明显变化，且随转速同步提升。将转速下降至10 000 r/min，振动值回归正常。

1 齿轮箱结构

齿轮箱通过斜齿一级减速，参数见表1。根据设备图纸，通过SolidWorks 软件对2 根转子进行三维建模。

表1 齿轮轴参数

2 转子固有频率及模态分析

2.1 模态分析理论

研究减速箱齿轮轴转子的固有频率和模态振型，首先要建立该轴的动力学方程，根据“动静法”，即达朗贝尔原理，运用静力学的方法分析和解决动力学的问题。在研究的转子系统中引入惯性力，建立动力学方程，将转子离散成n 个单元进行分析，对于一个多自由度线性系统，有阻尼的振动方程：+［K］{z}={F（t）}。式中，［M］为质量矩阵；［C］为阻尼矩阵；［K］为刚度矩阵；｛F（t）｝为外部激励阵列；为加速度阵列；为速度阵列；｛z｝为位移阵列。因为结构固有频率与所受外力｛F（t）｝无关，小阻尼对振型模态影响不大，因此，利用无阻尼无外载荷的自由振动方程求解结构的固有频率和振型，将上述方程简化为：+［K］｛z｝=0。

由于弹性体的自由振动可以分解为一系列的简谐振动的叠加，当发生简谐振动时，即为位移为正弦函数z=Usin（ωt）时，则方程为：。式中｛φ｝为各节点位移的振幅向量，即结构的固有振型；为此方程的根，也就是广义特征值；ωi为与振型箱对应的固有频率；由于｛φi｝为非零向量，要使方程有非零解，则，将结构离散为具有n 个自由度的系统，则刚度矩阵和质量矩阵都是n 阶矩阵，解上述的广义特征值方程即可得到弹性体的n 阶固有频率，从而确定对应的振型模态。

2.2 理论求解

查设备说明书得齿轮轴材料为18CrNiMo7-6，是EN 10084 表面硬化刚的牌号。材料参数如下：弹性模量E=2.1×1011N/m2；密度ρ=7800 kg/m2；泊松比μ=0.28；转子齿轮位置挠度；推算出轴的刚度。其中，L 为转子轴承位置间距，E 为弹性模量，I 为惯性矩，F 为外力。惯性矩I=，d 为轴径，得，代入数据k=1.629×107N/m。质量根据建模直接求得m=367.86 kg，固有频率计算公式ω0=，代入数据ω0=12 625.2 r/min。

2.3 导入模型

在ANSYS Workbench 中，将Modal 分析插入Workbench中，在Geomtry 中导入高速轴模型，对高速轴进行网格化，由于转子结构相对简单，采用几何自动生成法，根据物理模型自动离散生成有限元网格模型。然后在转子轴承位置施加固定（Fixed Support）约束。

2.4 结果分析

求得高速轴的6 阶频率（图1）和模态（图2），分别为：31.7 Hz、33.1 Hz、188.7 Hz、189.9 Hz、4510.8 Hz、8871.6 Hz。可以看出，前2阶临界转速在11 944.6 r/min 到12 472.08 r/min 之间，与理论求解值所差无几，非常接近实际振动跳车转速。从转子的临界转速计算可以看出，该减速机在设计过程中存在明显缺陷，转速范围内存在某一共振点，因此满足不了满负荷要求，只能将转速控制在11 000 r/min 以下才能避开共振点。

图1 高速轴6 阶频率

图2 高速轴6 阶模态

3 齿轮应力分析

分析齿轮啮合在不同转速工况下应力分布和应力大小的区别，从而了解齿轮工作状态下接触面的受力情况。

3.1 模型网格化

在ANSYS Workbench 中将statics tructure 分析插入Workbench 中，由于转子结构简单，在Geomtry 中导入转子模型（图3），并进行网格化，齿面进行智能细化（图4）。

图3 转子模型

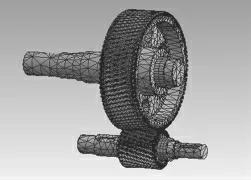
图4 模型网格化

3.2 建立边界条件

对比目前常用的集中边界条件下齿轮弯曲应力计算结果，根据对比结果，采用较为接近齿轮工作状态下的边界条件定义方式，对主动转子和从动转子施加径向约束，保留2 根转子的旋转自由度。由于本次研究的是不同转速应力差异，故未对齿面所受载荷做严密计算，对主动轮齿面施加负载转矩（T=500 N·mm），计算时间为1 s（图5）。

3.3 求解结果

图5 定义边界条件

分别设置转速500 r/min 和135 00 r/min 进行分析，计算对比不同转速下齿轮应力、应变和位移（图6、图7）。可以看出，不同转速下，应力分布从齿轮啮合开始到退出的接触路线与啮合状态基本一致，500 r/min 时应力最大0.037 MPa，13 500 r/min 时应力最大0.986 MPa。在转速较高的情况下呈现多齿啮合周期波动特征，而在低转速载荷工况下则表现为单齿啮合周期波动，且在低转速情况下应力上升较快，转速越高，应力变化越慢。

图6 500 r/min 转速下齿轮应力、应变和位移

图7 13 500 r/min 转速下齿轮应力、应变和位移

4 结论

采用ANSYS Workbench 有限元计算分析齿轮箱转子的固有频率和不同转速下齿轮受力情况。结果表明，齿轮转子在工作转速期间存在共振区，不同转速下，齿轮啮合受力分布均匀，低转速情况下应力变化较快，待转速提升，变化趋势逐渐趋于平稳，给机组因齿轮箱振动大跳车提供了数据支撑，为改进方向和措施提供参考。