球形电动机三维旋转运动轨迹插值算法

张宗楠，吴凤英，张冰娇

（天津理工大学 电气电子工程学院，天津300384）

三自由度永磁球形电动机作为新型电动机简化了机械结构.具有占用体积小，使用便捷，稳定性好等优势，且球形电动机运动复杂，所以有必要对其控制进行研究，而其中的轨迹规划及实现是其中重要一环.

球形电机运动轨迹是旋转运动轨迹，其轨迹表示方法、轨迹规划方法以及实现方法与传统机器人表示方法都不相同，现在针对球形电机轨迹规划研究相关文献较多，如安徽工业大学提出的B 样条轨迹规划、时间与能耗最优轨迹规划.天津大学提出的时间最优轨迹规划、避障轨迹规划[1-3].而对具体实现运动轨迹的插值算法研究较少，且传统的插值算法只用于实现二维或三维空间的平移运动轨迹，如机器人中常用的D-H 模型所用的直线插补算法、空间圆弧插补算法、B 样条插补算法[4-6].但是此类传统插值算法不能直接应用于球形电动机三维旋转运动的插值.所以本文提出一种基于欧拉角数字积分角度插补算法，此插值算法以传统数控系统中的数字积分法为基础，首先对球形电机建立运动学模型，通过逆运动学模型，求解出球形电机运动的欧拉角，并分析了欧拉角的奇异性问题，最后对三个欧拉角角度依次进行插补实现球形电机的运动控制.

1 三自由度永磁球形电机结构与工作原理

1.1 永磁球形电机装置结构

三自由度永磁球形电动机装置结构示意图如图1 所示.永磁球形电动机由半壳定子和球形转子构成，在球形转子的表面赤道平面装有p 对永磁极，且按照N、S 极依次分布，法兰安装在球形转子顶部，用以连接转子输出周和负载.定子为铝制空球壳，三层独立且平行的的定子线圈安装在定子球壳内部，每个线圈具有相同的空心结构和匝数，第二层的线圈放置在赤道位置，第一层和第三层的线圈对称的分布在第二层线圈两侧，也就是对称分布在赤道两侧，赤道两侧线圈的给个线圈轴线和赤道具有相同的夹角.

图1 球形电动机装置结构示意图Fig.1 Schematic diagram of spherical motor device

1.2 球形电机工作基本原理

球形电机运动原理如图2 所示.当定子线圈通电后，定子线圈就会产生旋转磁场，定子线圈产生的旋转磁场与转子上永磁体产生的静态磁场相互作用，从而产生一定的电磁转矩驱动永磁球形电动机的运动，通过控制大小不同的线圈电流，可以产生各种方向和不同大小的电磁转矩，转子输出轴可以做出自转、俯仰、偏航动作，从而实现球形电动机的三自由度运动.

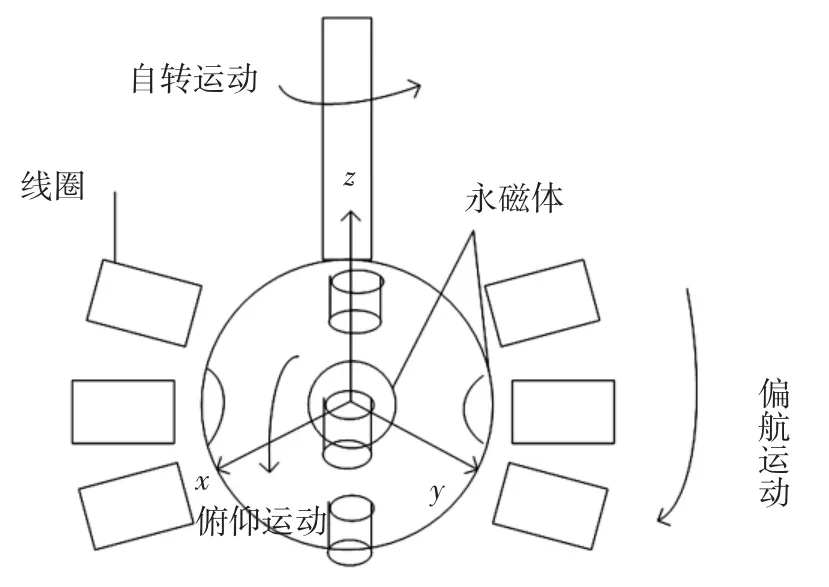
图2 球形电动机运行原理图Fig.2 Spherical motor operation schematic

2 建立球形电动机运动学模型

2.1 球形电动机正运动学

为了便于描述球形电动机球形转子的运动状况，需要对其刚体建立正逆运动学模型.本文采用欧拉角ZYX 旋转方式进行位姿描述，因为欧拉角表示法具有参数少、直观、物理意义明确，易于理解和应用等优点.

设定子的坐标系为xyz，球形转子的的坐标为abc，两个坐标的原点相重合，其中，定子坐标系为参考坐标系，转子坐标系为运动坐标系，球形转子的运动可以看做是运动坐标系绕参考坐标系旋转形成的，即转子坐标系abc 第一次旋转是绕c 轴从abc 坐标系旋转α 角，到达坐标系a1b1c1，第二旋转绕a1轴从坐标系旋转β 角，到达坐标系a2b2c2，第三次旋转绕c2 轴从坐标系a2b2c2 坐标系旋转γ 角到达坐标系abc.这三次旋转的变化矩阵为：

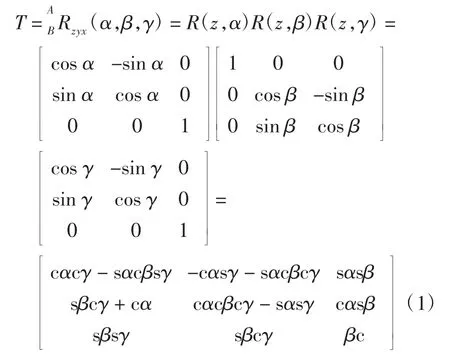
式（1）缩写符号分别为：角度余弦cos 简记为c，角度正弦sin 简记为s.

坐标变化关系示意图如图3 所示.

图3 笛卡尔坐标变换关系示意图Fig.3 Schematic diagram of Cartesian coordinate transformation

2.2 球形电动机正运动学

根据球形电动机逆运动学中已知旋转矩阵，可以求解出对应的欧拉角，将旋转矩阵表示如下：

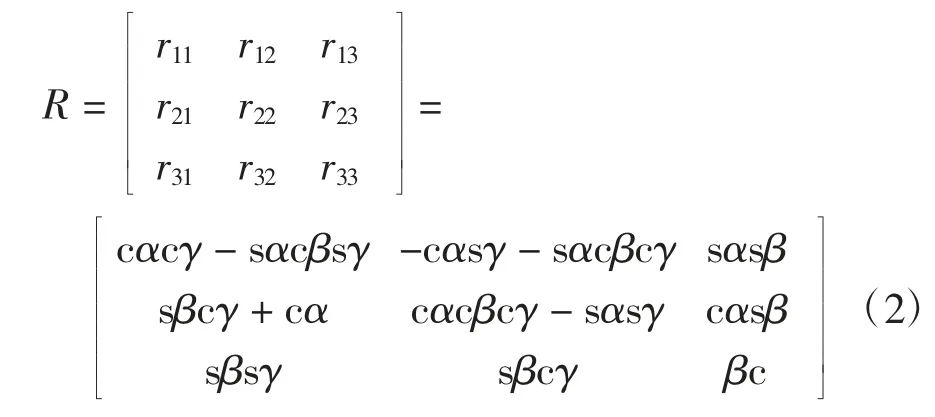
则可以表示如下欧拉角：

2.3 欧拉角奇异性分析

在数学中，奇异性通常指的是在一个点处，某个数学对象未被定义，或者一个集合中的某个点处的某个数学特性不好，比如不可微.在欧拉角描述钢体位姿的情况跟下也存在奇异性问题，所以在选取欧拉角描述的方式时，应当避开这种情况的出现.以前面所采用的ZYX 旋转方法为例，给定球形电动机一个姿态，是否只有一种旋转方法可以让基座坐标系和转子坐标系想重合，答案是否定的.当球形电动机Y 轴所指竖直向上时，此时但是α、γ 有多种方式，即存在不唯一解，比如不过球形转子的旋转运动被外面定子壳体所限制，各个欧拉角的角度旋转范围为180°≤α≤180°和-45°≤β、γ≤45°，所以采用ZYX 旋转方式并不会在球形电动机出现欧拉角的奇异性问题.

3 转子输出轴数字积分法角度插补原理

3.1 数学模型

已知在参考坐标系xyz 下转子输出轴的初始位姿是P，然后以Z-X-Z 欧拉角旋转方式分别旋转α、β、γ 角后，转子输出轴到达目标位姿点P′，根据Axis-Angle 理论，转子输出轴的转动可以看做是绕某一轴旋转θ 角后到达目标位姿，若以恒定的角速度ω 发生偏转，对应欧拉角α、β、γ 角以角速度ωα，ωβ，ωγ发生偏转，它们的关系式为：

式中，K为比例系数.

在Δt时间内欧拉角α、β、γ 角度增量Δα，Δβ，Δγ 应为：

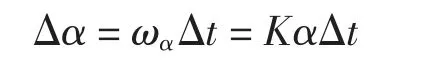
转子输出轴从起始位姿转向目标位姿的过程，可以看做是欧拉角α、β、γ 每一个单位时间间隔Δt分别以增量Kα、Kβ、Kγ 同时累加的结果.经过m次累加后，欧拉角α、β、γ 分别到达终点.

式中，K，α，β，γ 为常数，若取一单位时间间隔，Δt=1，则：

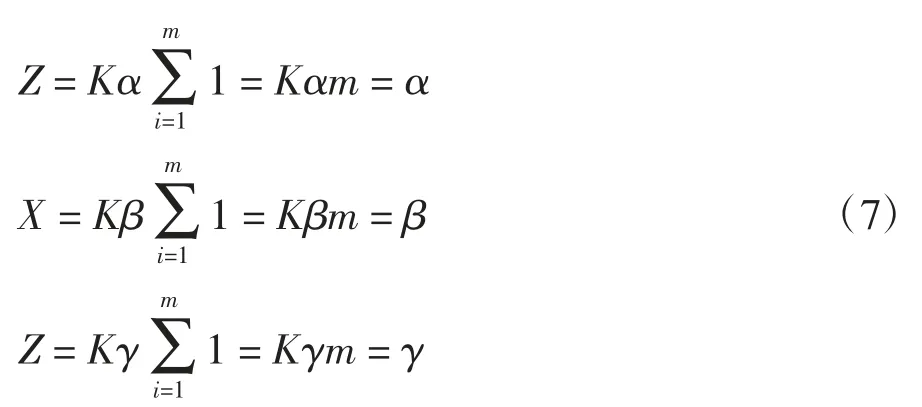
若这三式成立，那么：

上述所示公式表明了累加次数m和比例常数K的反比例关系上，如果m确定了，那么K也就确定了，不过累加次数m必须为整数，所以K一定是小数.K的取值主要考虑每次增量Δα、Δβ、Δγ 不大于1，以保证转子坐标系abc 每次分配给脉冲不超过一个，也就是说每次角度增量只产生一个单位步距角，即：

其中，Kα、Kβ、Kγ 为被积函数.

3.2 进给脉冲产生的方法

欧拉角α、β、γ 的最大容许值受系统中寄存器容量的限制，假如寄存器有n位，则α、β、γ 的最大允许寄存器的容量为2n-1（α、β、γ 为二进制数），满足Kα＜1、Kβ＜1、Kγ＜1，即：

由积分器框图4 可以看出，图中被积函数寄存器JωZ寄存Kα，累加寄存器JRZ寄存余数. 累加结果大于1 时，整数部分溢出作为进给Δα，小数部分存于累加寄存器JRZ中，待下次累加.

图4 积分框图及逻辑图Fig.4 Integration block diagram and logic diagram

显然，在做欧拉角角度插补时应实现的、和的积分运算.需要同时采用三个积分器同时分别进行，这样组成的数字积分器角度插补框图如图5 所示.

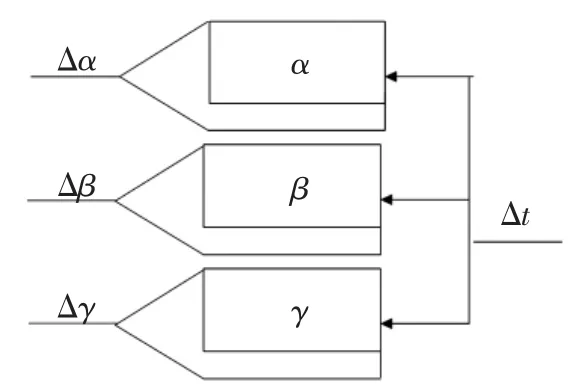
图5 数字积分器角度插补框图Fig.5 Digital integrator angle interpolation block diagram

4 转子输出轴插补流程及仿真验证

4.1 转子输出轴插补流程

已知定子壳体的静坐标系xyz 上起始位姿为，球形转子的动坐标系abc上的目标位姿为，经式（3）可以反解出球形电动机的欧拉角，再进行数字积分原理欧拉角轨迹插补算法.其算法流程如图6 所示.

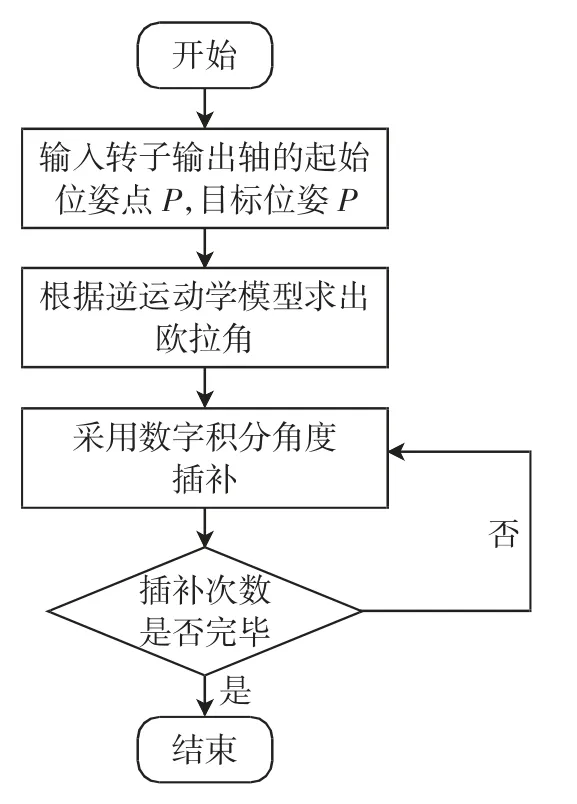
图6 球形转子插补流程图Fig.6 Spherical rotor interpolation flow chart

4.2 MATLAB 仿真

球形电机转子输出轴的转动可以分为三类，第一类是欧拉角α、β、γ 单独转动，因为只是绕不同的轴旋转，而旋转的原理则是相同的，所以只对欧拉角α 进行仿真插值，第二类是欧拉角α、β、γ 两两进行转动，同上原则一样，所以只选取α、β 的组合进行仿真插值，第三类是三个欧拉角α、β、γ 同时进行插值.

第一类欧拉角α 单独旋转，已知球形转子其实位姿为Rs1，目标位姿位姿为Re1.

根据图6 所示的球形转子插补流程图进行MATLAB 仿真，则球形转子轨迹插值仿真如图7 所示.

第二类欧拉角α、β 单独旋转，已知球形转子其实位姿为Rs1，目标位姿位姿为Re2.

则球形转子轨迹插值仿真如图8 所示.

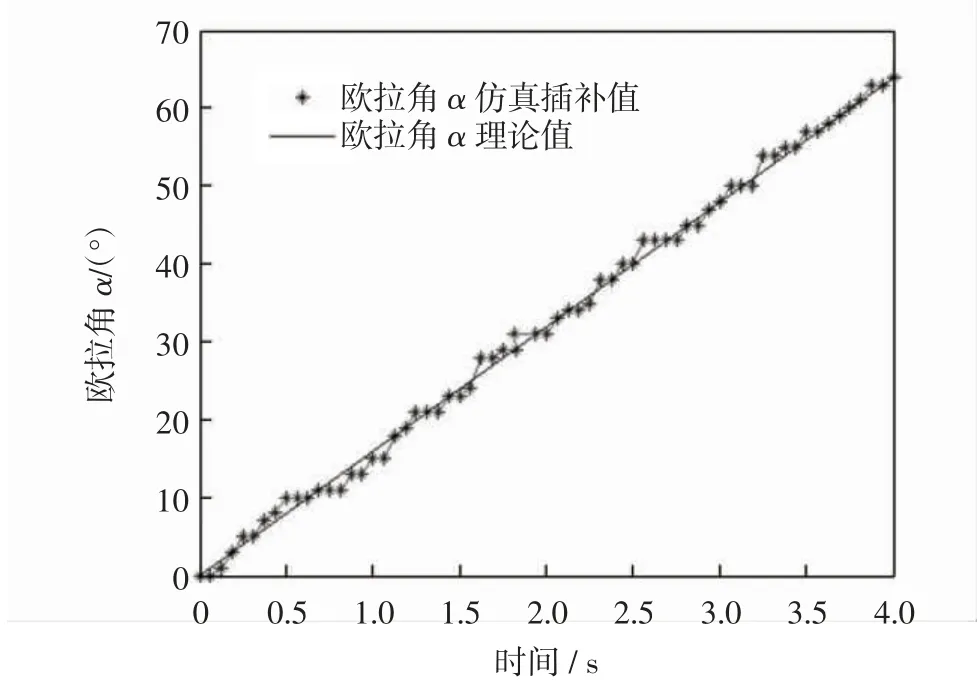
图7 欧拉角α 角度插值仿真图Fig.7 Euler angle α angle interpolation simulation diagram

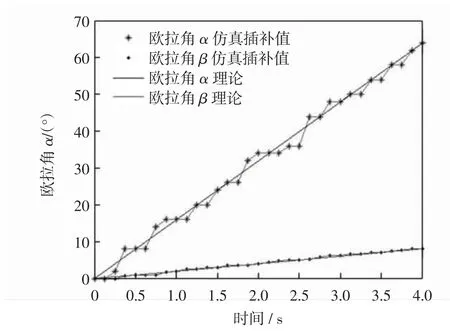
图8 欧拉角α、β 角度插补仿真图Fig.8 Euler angle α、β angle interpolation simulation diagram

第三类欧拉角α、β、γ 同时旋转，已知球形转子其实位姿为Rs1，目标位姿位姿为Re3.

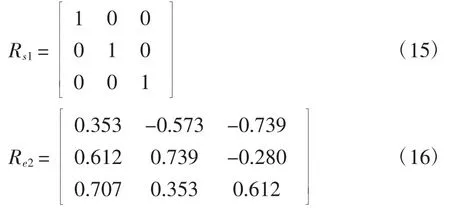
则球形转子轨迹插值仿真如图9 所示.

由MATLAB 仿真图可知，在三种情况下，欧拉角角度数字积分法的可行性，把三张仿真图相互比较可知，欧拉角各自角的插补过程是相互独立的，由图7 和图8 可知，当插值角度大时，插补速度快，插值角度小时，插补速度慢.这是因为角度的插补都是由m=2n次的累加运算，也就是插值时间是一定的，插补的角度越小则误差越小.

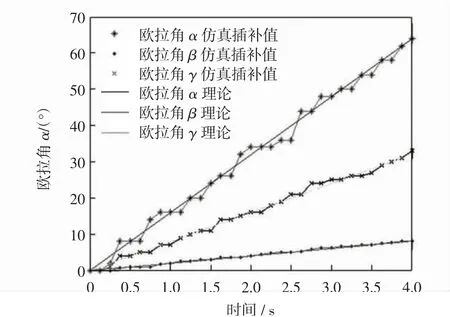
图9 欧拉角α、β、γ 角度仿真图Fig.9 Euler angle α、β、γ angle interpolation simulation diagram

5 结 论

本文提出了一种三自由度永磁球形电动机的数字积分角度插补算法，根据球形电动机的特殊的运动形式，并建立正逆运动学模型，详细的介绍了角度数字积分法的原理，在MATLAB 仿真平台上验证了球形电动机转子输出轴运行的三种不同运动情况，从而证明该方法的可行性，为后续的球形电动机的闭环控制提供了理论基础.