考虑单一枢纽点失效的中欧班列轴辐网络研究*

张琪胜，汤银英，陈 思

（1 西南交通大学交通运输与物流学院 硕士研究生, 四川 成都611756；2 西南交通大学交通运输与物流学院 副教授、博士,四川 成都611756；3 西南交通大学交通运输与物流学院 讲师, 四川 成都611756）

0 引言

中欧班列是指按照固定车次、 线路等条件开行，往来于中国与欧洲及一带一路沿线各国的集装箱国际铁路联运班列。 截至2019 年3 月底，其累计开行数量已超过14 000 列， 国内始发城市现有48个，境外到达城市44 个，运行线65 条。 中欧班列因理念新颖和政策优势而备受关注，但是，其自身存在线路重复、无序竞争以及由国内国际环境不确定性导致的关键节点拥堵失效风险等问题。 因此，研究中欧班列轴辐网络，对完善“干支结合、枢纽集散”的班列组织模式，降低成本，提高运输效率具有重要意义。

目前对于中欧班列的研究多集中于存在问题、发展对策等定性方面，仅有少量学者采用模型量化方法对网络优化和开行方案等方面进行了研究。 文思涵等[1]以单一方向去程班列（中国—欧洲）为研究对象，借鉴选址—运输路径安排思路，研究网络优化问题。 李天昊等[2]依据节点功能差异，设计节点分级系统，以此为基础建立开行方案模型。 王娇娥等[3]构建高、中、低三种运价水平，利用距离—经济成本分析方法划分满洲里、二连浩特和阿拉山口的腹地范围，并根据现实情况识别枢纽城市。

为降低运输成本，实现规模效益，诸多学者提出了轴辐式中转集结的思路。 轴辐式网络综合了设施选址和路径安排两个问题，O’Kelly[4]建立单分配模式下单枢纽系统和双枢纽系统轴辐网络模型，并指出轴辐网络的基本原理是通过少量的弧连接大量OD 点进而减少必经路线。Mohammad 等[5]将失效分为部分失效（服务速率下降）和完全失效（无可用性）， 并提出一种基于遗传算法和帝国竞争算法的新型混合自适应启发式算法求解轴辐模型。 An 等[6]提出可靠轴辐网络设计模型，模型考虑备用节点和备用路线的选择，并使用拉格朗日松弛算法和分支定界法对模型进行求解。 胡晶晶等[7]研究备份枢纽的选择问题， 并通过线性化方法转化模型为线性，使用数学求解器CPLEX 求解小规模问题， 使用遗传算法求解大规模问题。

轴辐式网络的优势在于以较少路径连接网络，可以降低运输成本，产生规模效益，其缺陷在于网络形成之后，一旦枢纽节点发生故障其恢复成本较高， 因此在建立模型时有必要考虑网络的可靠性。本文针对集散过程中可能出现的枢纽节点失效，考虑因此产生的货流阻断和延迟，引入备选节点和拥堵成本，构建中欧班列轴辐式运输网络。 同时，因数据源规模较小， 在求解模型时使用商业优化软件CPLEX 进行求解。

1 单分配轴辐网络模型

1.1 单分配轴辐式网络拓扑结构

单分配轴辐式网络是指网络系统中每个非枢纽节点仅分配给某一个枢纽节点，非枢纽节点通过和枢纽节点相互作用，实现货流、客流及服务传递的一种网络结构，基本拓扑结构如图1 所示。 现阶段，中欧班列运量较小且方向单一，较为适用单分配轴辐网络。

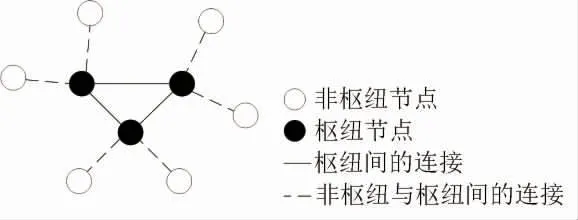
图1 轴辐式网络拓扑结构

对于单分配轴辐网络，O’Kelly 最早提出从p-HMP(p-枢纽中位问题)角度解决轴网络设计问题的思路。 为合理简化研究，提出假设：网络中节点与节点之间相互畅通， 轴辐网络中非枢纽点不互连，即非枢纽之间的流量必须至少经过一个枢纽点进行转运。

1.2 单分配轴辐式网络模型描述

单分配轴辐式网络模型的目标为最小化网络整体运输成本，包括非枢纽节点和枢纽节点之间的支线运输成本， 枢纽节点之间的干线运输成本，运输路线可以描述为i→k→m→j。 引入如下符号来描述。

N：中欧班列轴辐网络中总节点集合，N={1,2,...,n}；

p：设定枢纽节点个数p＜n；

ρ：枢纽节点之间因规模效益产生的折扣系数；

cij：节点城市i到节点城市j的每公里单位集装箱运输成本；

dij：节点城市i到节点城市j的距离；

Cij： 节点城市i到节点城市j的单位集装箱运输成本；wij：节点城市i到节点城市j的集装箱运量；

yik：非枢纽节点的分配，若将节点i分配给k则取1，否则取0；

yikmj：表示OD 流i→j所经过的路径，若i→j的集装箱流经过枢纽k→m则取1，否则取0。目标函数见下式：

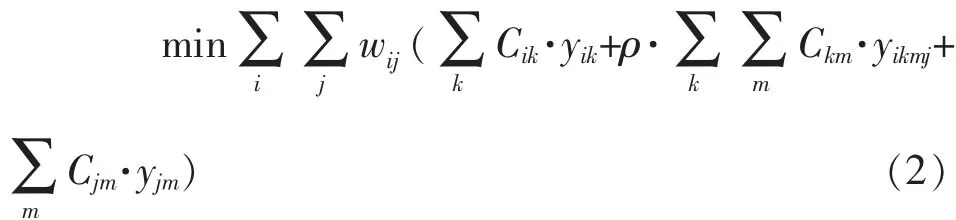
1.3 单分配轴辐网络结构约束

在最小化网络整体运输成本的目标下，单分配轴辐网络受到网络结构的约束， 包括节点分配约束，路径约束，枢纽数量约束，纯轴辐约束和决策变量的0-1 约束。

1.3.1 节点分配约束

网络拓扑结构为单分配模式，即每个非枢纽节点能且只能与一个枢纽节点相连接。

1.3.2 路径约束

从始发节点i至目的节点j的流量经过路径需包含枢纽转运k→m。

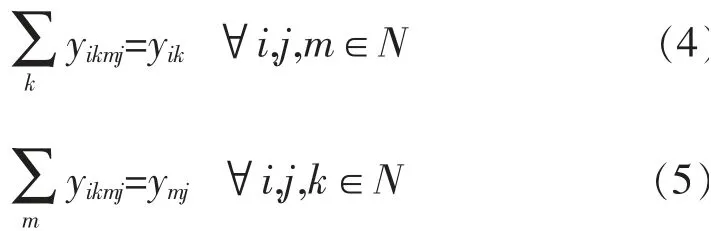
1.3.3 枢纽数量约束

枢纽数量根据运营方的实际需要设定，在模型中作为已知参数

1.3.4 纯轴辐约束

单分配轴辐网络要求非枢纽节点之间不互相连接， 即对于任意OD 流均采用在枢纽点中转集结方式运输。

1.3.5 0-1 约束

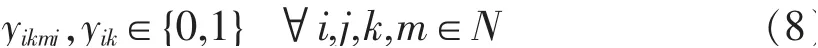
2 中欧班列轴辐网络模型

2.1 模型改善与假设

对中欧班列而言，单纯的轴辐式网络适应性有所欠缺，与班列现实情况具有一定差异，因此需对模型进行适当改善，另需考虑枢纽点失效情形。 本文涉及到的失效情况分为两种，一种为枢纽节点的可使用性完全丧失，即完全失效；另一种为枢纽节点的容量超出限制产生拥堵，即部分失效。 中欧班列轴辐网络的枢纽选址问题是在单分配轴辐式网络选址的基础上， 考虑枢纽节点的完全失效概率，引入备选节点和拥堵成本；而路径安排问题，对于枢纽点失效后的货物流动分为两部分考虑，一部分为从失效点始发或终到的货源因节点的可使用性完全毁灭，故定义为货源流失；另一部分为失效点仅作为中间枢纽点的货流，路径转经备选节点[8]。 另需作出如下假设：

1） 仅考虑单一枢纽节点的失效问题，且已知失效概率为q；

2） 枢纽点失效后，备选节点将仅从其他未受影响的枢纽中选择；

4） 拥堵成本定义为超过容量限制的货物流量的一次函数；

5） 枢纽节点失效时产生的货源流失成本，引入惩罚系数α。

2.2 目标函数

中欧班列轴辐网络目标函数为最小化网络整体运输成本，具体又可以分为常规运输成本、路径重置成本、货源流失成本和拥堵成本四部分。 引入如下符号来描述：

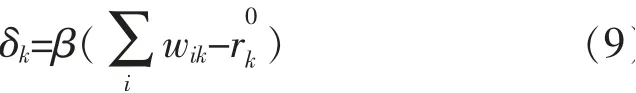
δk表示拥堵成本，采用超过容量限制的货物流量的一次函数表达，其中β 为拥堵成本系数。表示当枢纽节点k失效时， 枢纽点l作为备选枢纽继承枢纽k的流量， 若l成为k的备选点则为1，否则为0。

2.2.1 常规运输成本CMC

常规运输成本表示未受枢纽失效影响部分的网络运输成本。

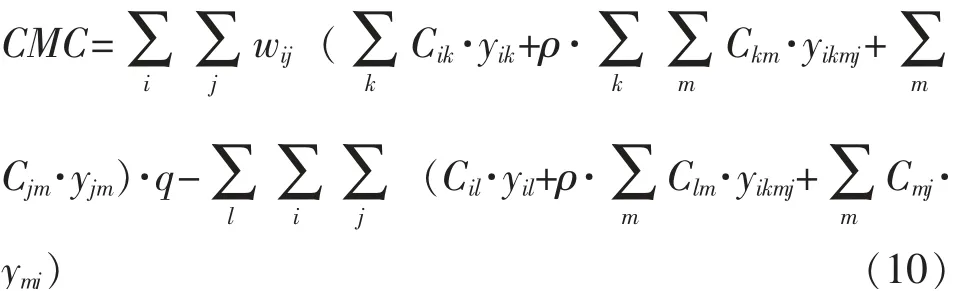
2.2.2 路径重置成本RTRS

路径重置成本表示因枢纽节点失效，原经由失效节点的货流转向备选节点的路径重置成本。 即原i→j的路径i→k→m→j转换为i→l→m→j。

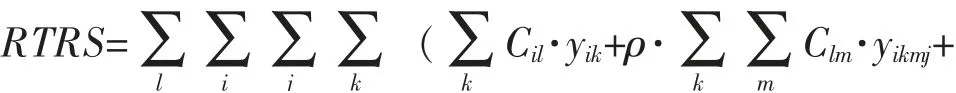
2.2.3 货源流失成本FL

货源流失成本表示因枢纽节点完全失效导致的该节点作为始发或终到节点的集装箱货源流失。

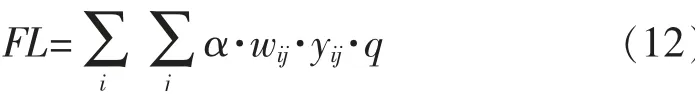
2.2.4 拥堵成本CG

拥堵成本表示备选节点原集结流量及因路径重置需转化为该节点集结的流量和。

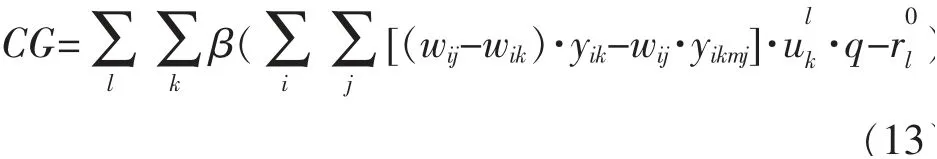
最小化网络整体运输成本目标函数如下：

2.3 备份约束

中欧班列轴辐网络以备选枢纽的方式考虑枢纽节点的失效问题，故需对枢纽的备份进行约束。

2.3.1 备选集约束

由前文可知，某枢纽节点的备选节点集合包含除本身以外的其他枢纽节点。

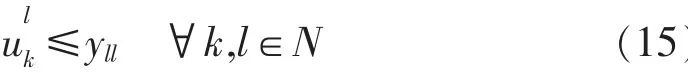
2.3.2 备选数量约束

每个枢纽节点有且仅有一个备选节点。

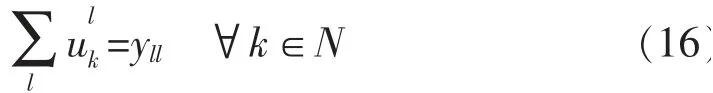
2.3.3 0-1 约束

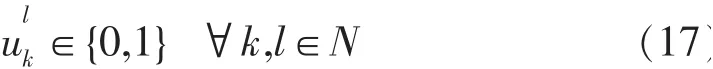
本文构建的中欧班列轴辐网络模型涉及原枢纽节点和备选节点的选择，为单目标非线性整数规划，具有一定的复杂性，需要将非线性部分转化为线性，本文采用变量替换的方法进行线性化。 引入

zikl=1 表示节点i分配到节点k， 并且节点k的备选节点为l。

xiklmj=1 表示从i到j的流量所经过的路径为i→k→m→j，且当枢纽k失效后转由枢纽l中转。

此外， 需要对新增的决策变量zikl，xiklmj进行约束，因模型目标为min 型，故：

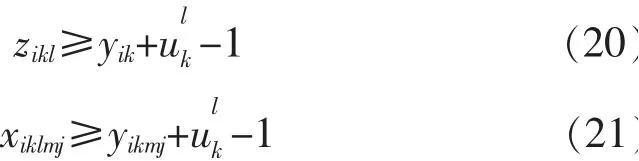
3 算例分析

3.1 基础数据

本文选取常态化开行的中欧班列主要节点城市作为研究对象，节点集合为{重庆（1）、郑州（2）、武汉（3）、成都（4）、合肥（5）、义乌（6）、长沙（7）、厦门（8）、西安（9）、昆明（10）、苏州（11）、沈阳（12）、营口（13）、杜伊斯堡（14）、汉堡（15）、蒂尔堡（16）、鹿特丹（17）、华沙（18）、罗兹（19）、布列斯特（20）、明斯克（21）、莫 斯 科（22）、帕 尔 梅 杜 采（23）、马 德 里（24）、布达佩斯（25）}，节点总数n=25，设置枢纽节点数量p=5，货源流失惩罚系数α=2，折扣系数ρ=0.750 0，失效概率q=0.050 0，拥堵成本系数β=2，枢纽节点容量限制

各节点之间的距离采用地图网站所搜集的铁路营运里程，每公里单位集装箱运输成本因国家不同而有所区别，根据调研结果，独联体国家铁路成本0.250 0 美元/（km·箱），欧洲铁路成本1.978 0 美元/（km·箱）， 国内段线路成本0.700 0 美元/（km·箱）， 城市节点之间的每公里单位集装箱运输成本采用途经区域各铁路成本的平均值进行近似计算，节点城市i到节点城市j的单位集装箱运输成本由公式（1）计算可得。 城市节点之间的集装箱周运量根据中欧班列各平台公司的实际情况进行合理预测。

3.2 模型求解

单分配轴辐网络模型为单目标线性规划问题，采用商业优化软件CPLEX 求解模型最优解， 最优成本为12 998.598 3 万美元，求解结果见表1。

表1 单分配轴辐网络模型求解结果

算例结果采用如下形式表述{枢纽点（备份点）|分配到该枢纽点的非枢纽点}，则单分配轴辐网络模型最优结果为{重庆| 成都、昆明}，{合肥| 郑州、武汉、义乌、长沙、厦门、苏州、沈阳、营口}，{鹿特丹|杜伊斯堡、汉堡、蒂尔堡}，{布列斯特|华沙、罗兹、明斯克、莫斯科、帕尔梅杜采、布达佩斯}，{马德里|}。

中欧班列轴辐网络原始模型为单目标非线性整数规划问题， 线性化后转化为单目标线性规划问题，模型变量个数为(26^5+26^4+26^3+26^2)=12 356 604，采用商业优化软件CPLEX 进行求解， 可得到模型的精确求解结果。 枢纽节点选择，非枢纽节点分配以及备选节点选择的求解结果见表2。

表2 中欧班列轴辐网络模型求解结果

中欧班列轴辐网络规划所得结果为{成都（西安）|重庆、长沙、厦门、昆明}，{西安（成都）|郑州、武汉、合肥、义乌}，{沈阳（西安）|苏州、营口}，{杜伊斯堡（华沙）|汉堡、蒂尔堡、鹿特丹、马德里}，{华沙（杜伊斯堡）|罗兹、布列斯特、明斯克、莫斯科、帕尔杜比采、布达佩斯}，中欧班列轴辐网络规划示意图如图2 所示。

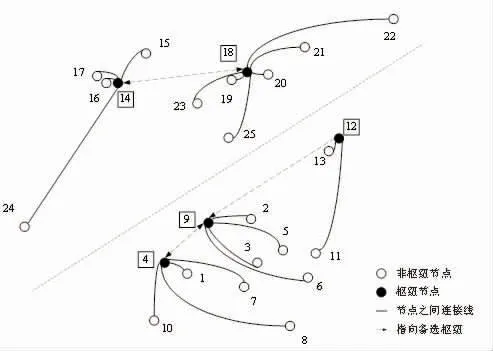
图2 中欧班列轴辐网络示意图

单分配轴辐网络与中欧班列轴辐网络不同之处在于枢纽的可靠性在网络设计阶段是否被考虑在内。 单分配轴辐网络缺少对枢纽点失效与拥堵的考虑，但是枢纽点仍有发生故障的风险，本文根据实际情况对失效发生时各枢纽的替代方案如下：{重庆（合肥）}，{合肥（重庆）}，{鹿特丹（布列斯特）}，{布列斯特（鹿特丹）}，{马德里（空）}，两种网络对比结果见表3。

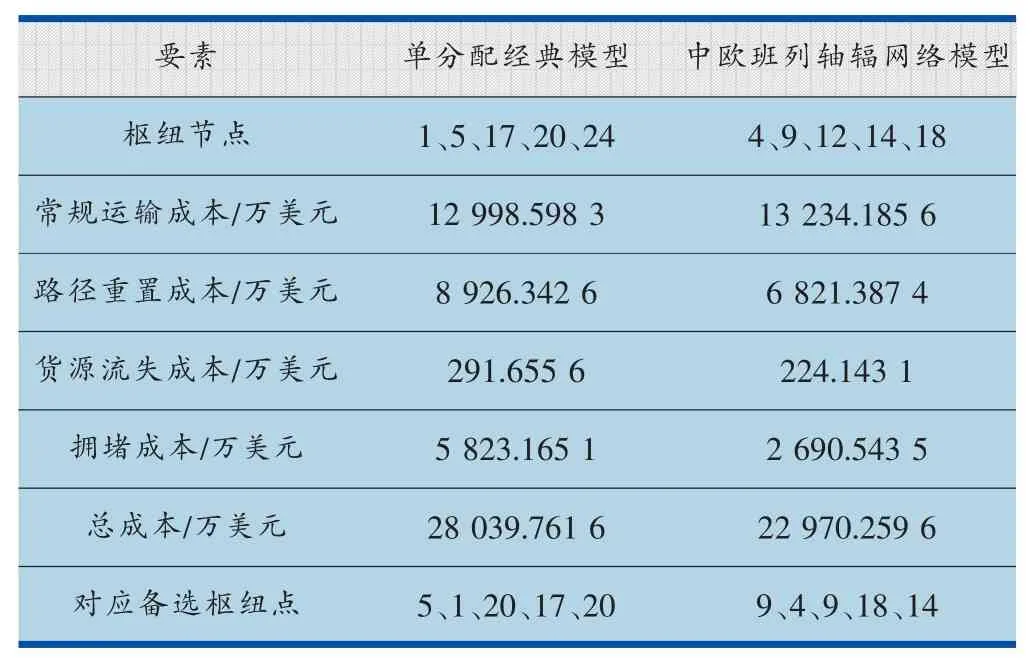
表3 单分配经典模型与中欧班列轴辐网络模型主要要素对比表

轴辐式中转集结的班列组织模式可以有效解决点对点直达所产生的一系列问题，但是中欧班列对所经过的关键节点的掌控性较差，关键节点能够分配给中欧班列的能力也有限，即关键节点存在拥堵及不可用的风险性。 此外，轴辐式运输网络中的货流由非枢纽节点集中到枢纽节点产生规模效益，由此也提高了枢纽节点在网络中的地位，一旦枢纽节点发生故障，其影响是巨大的。 上述算例表明，在网络设计阶段不考虑枢纽节点失效和拥堵时，一旦枢纽的可使用性毁灭，路径重置成本、货源流失成本和拥堵成本是比较大的。 反观考虑枢纽失效和拥堵时，除因部分非枢纽节点需集结至枢纽产生绕道成本导致的常规运输成本较大以外，其余各项成本均较小，总运输成本较原始网络也减少18%。 由此可见，设置合适的备选枢纽节点，可以降低外界因素对中欧班列运输网络正常运营的影响，提高网络的可靠性。

4 结论

随着中欧班列的爆发式增长，各班列公司的竞争将更加激烈， 点对点直达组织模式将达瓶颈期。与之相比，轴辐式中转集结模式更有利于提高资源利用率，改变竞争现状。 中欧班列运输网络的构建需要考虑其去回程货源的不均衡性，同时，为缓解失效及拥堵的影响，本文提出的轴辐式网络模型在严格单分配p-hub 选址问题的基础上，考虑枢纽节点失效和拥堵的可能性，对每个枢纽节点设置失效概率、定义拥堵成本、选择备选枢纽。 此外，根据中欧班列实际运行情况设计算例求解模型，结果表明，为每个枢纽节点设置备选点可以提高网络的可靠性。

本文研究对象为单分配轴辐网络，而实际有可能出现多分配情况；本文假设某一时间段内仅有一个枢纽节点发生失效且备选节点仅可以从现有枢纽节点中选择，现实情况可能出现除枢纽点以外的其他重要节点失效，某一段时间内同时出现多个枢纽失效以及选择非枢纽点作为备选节点的情况。 下一步研究工作应该考虑多枢纽失效，备选节点不定的复杂情形。