澜沧江流域枯水年发电效益与下游生态-出境水互馈博弈研究

蔡方园，何艳虎，陈晓宏

（1.中山大学 水资源与环境研究中心，广东 广州 510275：2.广东工业大学 环境生态工程研究院，广东 广州 510006：3.中山大学 地理科学与规划学院，广东 广州 510275）

1 研究背景

水是人类赖以生存和发展的战略性资源，而随着社会经济和人口的快速发展，水资源开发利用和配置过程中潜在的矛盾也愈加显著［1］，尤其是水电能源的开发［2］。由于河流水电开发，大坝拦蓄天然径流，改变河流水文情势［3］，这对于流域的生态环境以及下游人民社会福利等方面存在一定的负面影响。故河流水电开发中的水资源利用竞争博弈与优化配置问题不容忽视。

澜沧江-湄公河是一条国际河流，涉及沿岸多个国家社会和人民的经济利益，在澜沧江流域进行水电工程开发是极具战略挑战意义的，很多学者都对此流域的水电开发、防洪、河道生态环境和航运等综合利用目标之间的竞争关系进行了研究。例如，李栋楠等［4］以澜沧江流域中下游三座梯级水库为例，同时考虑发电目标和生态约束，构建了梯级水库调度模型以定量分析发电和生态流量约束之间的均衡关系，发现二者之间呈现出非线性的竞争关系；魏国良等［5］以漫湾水电站为研究对象，建立了水电开发对河流生态系统服务功能影响的评价指标体系，评估结果表明漫湾水电开发虽然获得了正面的发电经济效益，但是生态环境方面牺牲的成本是生态效益的5.56倍，经济效益的背后是极大的环境代价，可见澜沧江水电开发和流域生态之间的矛盾颇为显著。

流域水资源优化配置的研究由来已久，成果丰富［6］，各种优化算法模型广泛应用，例如多目标遗传算法［7］、报童模型［8］等。而近年来，博弈相关理论与模型在解决水资源利用冲突和利益分配问题上的优异表现［9］使学者们将目光聚焦于此。Zhenliang Liao等［10］发现，湄公河流域沿岸国家围绕该河流的水资源使用问题，尤其是在上游修建梯级水库的行为上历来存在许多争执，作者在文章中基于合作博弈理论设计了一款“湄公河”游戏对如何解决跨界河流上的水坝建设与流域收益分配问题进行了探究。Yang Yu等［11］在澜沧江-湄公河流域对中国梯级水库系统运行和湄公河下游国家的水资源利用进行了合作博弈分析，发现中国的梯级水库运作会影响湄公河下游流量的时空分布，若中国参与合作联盟，那么在流域系统层面上将会带来更多的收益。尹云松等［12］熟练运用进化博弈理论，使得有限理性的流域通过学习和协调，能有效提高自身理性程度并调整对策，最终实现具有一致性的水资源数量和质量分配上的纳什均衡。付湘等［13］在研究中对多个水资源竞争用户进行了合作博弈和非合作博弈的效益差异探讨，结果发现，采取合作博弈能获得更高的总效益且实现帕累托最优，而且合作博弈的效益分配机制还能驱使行动占先者加入合作联盟。Chih-Sheng Lee等［14］基于水库流域管理出现的多项河道外供用水冲突，建立了多目标博弈理论模型，以期平衡流域经济发展和环境保护。何艳虎等［15］为优化流域配水方案，构建了引入奖励和惩罚因子的行业配水权重博弈模型，并在东江流域取得了客观合理的结果。

将博弈相关理论运用于分析跨境国际河流的河道内用水，有助于深入认识水电开发效益与河道生态需水、出境流量等的互馈竞争关系，寻求更为合理的解决方案。以澜沧江干流为例，水电站发电效益由水库发电流量和水头决定，水库发电下泄水量会导致水库蓄水量减少，水头降低，影响后续发电效益；而水库下泄水量与下游河道的生态需水流量存在重叠关系，水库下泄水量越多，能使得下游河道的生态需水和出境水满足度越高。若水库为满足下游河道内生态需水和出境流量的要求无约束泄流，必然导致枯水年水库蓄水减少、水头降低、发电效益受损，此时水电站发电效益最大化和下游的生态需水、出境流量满足程度最高之间就存在竞争博弈关系。因此，本文欲以澜沧江干流景洪水电站为研究对象，引入博弈理论，构建水电站发电效益与下游河道内生态需水-出境水的完全信息静态博弈模型，并耦合支付函数最大化计算方法，在来水量一定的总约束下，分析水电站发电效益（由发电流量和发电水头反映）与下游河道内生态需水-出境水之间的竞争博弈关系，并依据纳什均衡准则计算获得综合效益最大化下的流域水库调蓄与下游河道用水协同调控方案。

2 研究区域概况

澜沧江-湄公河是一条国际河流，在中国境内河段称为澜沧江，出境后河段称为湄公河。澜沧江全长2160 km，平均比降2.12‰，流域面积17.4万km2。根据2003年全国水力资源复查成果，澜沧江流域水力资源技术可开发装机容量34 840 MW，年发电量1690.33 亿kW·h，水力资源极其丰富，是我国重点开发的十三大水电基地之一。景洪水电站是澜沧江干流最后一个具有径流调节能力的梯级电站，坝址距离澜沧江出国境口仅108.9 km，河流出境流量近似等于水库下泄流量。因此，景洪水电站的水资源合理调配对维护中国和湄公河下游国家的共同利益至关重要。

景洪电站水库死水位591 m，正常蓄水位602 m，校核洪水位609.4 m，相应的死库容为5.62亿m3，正常蓄水位以下的库容为8.71亿m3，总库容11.39亿m3，为不完全季调节水库。坝址处多年平均径流量1830 m3/s［16］。电站下游河道枯水期水面水位约538 m，汛期水位抬高，两年一遇的设计洪水位为544.9 m。本文中坝址下游河道的水位流量关系曲线借鉴李廷华［17］根据允景洪水文站历史洪水数据资料推求的结果，即水位H（m）—流量Q（m3/s）：

由式（1）可以计算出景洪水电站坝址处两年一遇洪峰流量约为7000 m3/s。

景洪水电站总装机容量为1750 MW，发电额定水头为60 m，最大发电流量为3328 m3/s，单库多年平均年发电量为78.58亿kW·h。

景洪电站装机容量大，河道落差大，水能资源丰富，发电效益高；电站建成后，景洪市政府规定，该市的城市用水将直接从电站库区取水，取水流量为1.73 m3/s；由于澜沧江在流经景洪电站后，下游沿江地势豁然开阔，大部分土地利用类型属于耕地，目前防洪标准较低，而且景洪电站调节库容较小，若单独运行只能保证自身枢纽的防洪要求，无力也无需承担下游地区的防洪任务［18］，所以，当汛期景洪水电站来水流量达到两年一遇的洪水时（洪峰流量约为7000 m3/s），为了减少弃水、增加蓄水以最大化发电效益，水库最高蓄水位调整为校核洪水位，并规定在洪峰出现后的7天内调整水库水位回落到正常蓄水位，保障坝体自身安全；此外，澜沧江沿岸生物物种丰富而且比较脆弱，同时河流的生态健康也影响着下游国家的综合利益，故景洪水电站在发挥综合效益时，须保证河道内生态需水得到满足，出境水量不低于504 m3/s［19］，使河流能够健康可持续地给沿岸国家与人民带来利益。综上所述，景洪电站的开发任务确定为以发电为主，同时需满足河道内生态需水和出境流量的要求。

3 研究方法

3.1 博弈论与完全信息静态博弈博弈论是关于策略相互作用的理论，构成一个博弈的基本要素至少包含以下4个：博弈参与对象、博弈规则、博弈策略和博弈的支付。其中，博弈规则包括行为、时间和信息3个关键内容。

在博弈中，如果参与对象采取行动的次序无先后之分，且对其他参与对象的特征、类型以及可以选择的战略和在此战略下所能得到的支付等信息掌握得充分，我们将这类博弈称为完全信息静态博弈［20］。

本文欲在来水总量确定的情况下，探究水电站发电效益与下游河道内生态需水-出境流量之间的博弈竞争关系该如何协调，以期达到综合效益最大化的纳什均衡状态。在博弈过程中，假定水库发电效益与河道内生态需水-出境需水这三者采取策略的次序无先后之分，且相互之间的行为特点和阈值区间是已知信息，可选策略以及在此策略下能得到的支付或效益亦为已知信息，那么就构成了一个完全信息静态博弈问题。

3.2 完全信息静态博弈模型在明确一个博弈的基本构成要素之后，根据这些要素，运用博弈论规范的数学语言及概念构建博弈模型。有多个对象参与的博弈模型W的一般表达式如下：

式中：X为博弈参与对象x的集合，x∈X：Sx为每个博弈参与对象x的策略集合：S *为博弈均衡策略：U为博弈参与对象的支付函数集合。

3.3 纳什均衡纳什均衡（Nash Equilibrium）的概念，最早是由Nash（1950，1951）提出的，其数学定义是：

在由X个参与对象组成的博弈中，策略组合s=(s1，s2，s3，…，sX)构成一个纳什均衡，当且仅当：对于每一个博弈参与对象x，x=1，2，3，…，X，其策略sx是对策略组合s中的其他所有博弈参与对象策略s-x的最优回应，即对任意s′x∈Sx，U(sx，s-x)≥U(s′x，s-x)［21］。

通俗来讲，一个纳什均衡就是所有博弈参与对象的一个策略组合。这个策略组合的每个策略都与其他策略构成相互最优反应，一旦实现相互最优，所有博弈参与对象都将不会单方面改变策略，因此会形成均衡状态。纳什均衡的实现要求所有博弈参与对象的均衡策略是共同认识，也就是完全信息博弈的概念。本文根据研究对象的特点和研究目的，通过构建完全信息静态博弈模型，以期达到纳什均衡。

4 景洪水电站发电效益与下游生态需水—出境流量互馈博弈分析

4.1 完全信息静态博弈模型构建景洪水电站在来水量一定的约束下，水库发电效益与下游河道内生态需水—出境流量的完全信息静态博弈模型记为W=(X，Sx，S *，U)，具体构建如下：

（1）参与对象集合。参与对象集合记为X={水电站发电效益，下游河道内生态需水流量，出境流量}。

（2）各参与对象的策略集合。Sx为各参与对象的策略集合（即水电站发电效益与下游河道内用水的协同调度方案）。其中，参与对象1—水电站发电效益的策略集合：S1={Qi}，（发电效益由发电流量与水头反映，水头可通过水库蓄泄过程中的水量平衡关系和水位-库容曲线用发电流量表示，因此发电效益策略简化为发电流量Qi表示）；参与对象2—下游河道内生态需水流量的策略集合：S2={EFRi}；参与对象3—出境流量的策略集合：S3={Q出境i}；i=1，2，…，T，i为参与对象的行动时段，T为行动时段总数。各参与对象所有策略选择所形成的集合成为博弈的策略集合，记为Sx={S1，S2，S3} 。

（3）支付函数。水电站发电效益与下游河道内生态需水流量、出境流量这三个博弈参与对象在各种行为策略组合下的支付函数记为U，在每一种策略组合m下，支付函数Um为：

其中：式（3）Um为所有博弈参与对象的总支付函数，表示策略组合m下的总效益；

式（4）定义Um1为策略组合m下博弈参与对象1--发电效益的支付函数，等于年内实际发电量Em与景洪电站多年平均年发电量78.58（单位：亿kW·h）的比值，即发电效益指数；

式（5）定义Um2为策略组合m下博弈参与对象2--河道内生态需水流量的支付函数，等于水库下泄流量满足生态需水流量的时段数（记为∑dem）占总计算时段数（T）的比例，即生态效益指数。

式（6）定义Um3为策略组合m下博弈参与对象3--出境需水流量的支付函数，等于水库下泄流量满足出境需水流量的时段数（记为∑dcm）占总计算时段数（T）的比例，即出境效益指数。

耦合支付函数最大化方法进行博弈计算，鉴于发电效益这一博弈要素易于量化表述，因此将发电效益最大化作为主要目标，下游河道内生态需水和出境需水以约束条件的形式参与博弈。

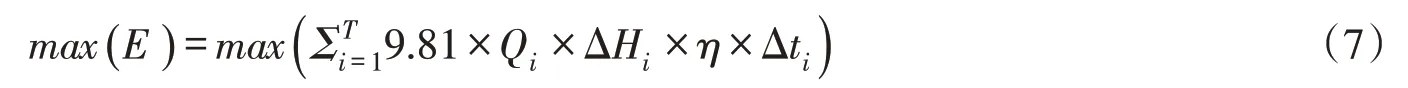
约束条件如下：

电站出力约束

式中：Ni为i时段电站实际出力，kW；Qi为i时段发电流量，3328 m3/s为景洪电站正常运行下的最大允许发电流量［22］；ΔHi为i时段发电净水头，m；η为发电效率，一般取0.7～0.9，这里取0.9；Hi、Hi+1分别为i、i+1时段的水库水位，m；H下指水库下游河道内水位，m；根据李廷华［17］关于景洪水电站下游河道内水位-流量关系的相关研究，分2种情况（a）当Q下泄i≤2000m3/s时，该计算时段i处于枯水期，取下游河道内水位H下为定值538 m；（b）当Q下泄i＞2000m3/s时，下游河道内水位按式（1）计算，为H下=0.0014*Q下泄i+535.2。

水量平衡关系及库容约束：

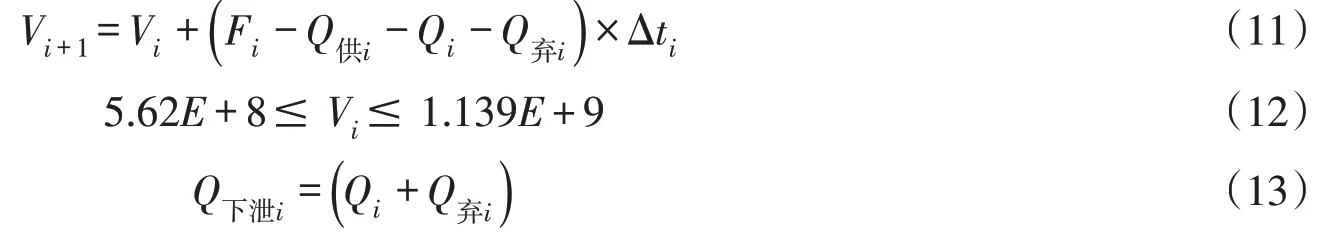
式中：Vi指i时段水库库容，m3，允许库容范围在死库容5.62亿m3和总库容11.39亿m3之间；Fi为i时段水库来水流量，m3/s；Q供i是指i时段城市供水取水流量1.73 m3/s，假定保证率为100%；Qi为i时段发电流量，m3/s；Q弃i为i时段不经过发电机组直接下泄流量，m3/s；水库总下泄流量Q下泄i为水库i时刻的发电用流量和水库i时刻弃水流量之和，m3/s；Δti=24×3600，用以将发电出力计算时段单位从日换算成秒。

水库水位约束：

式中：Hi为i时段水库水位。式（14）是景洪电站水库的水位-库容曲线，水库水位变化范围在591 m（死水位）与609 m（校核洪水位）之间。

河道内生态需水及出境流量约束：

式中：EFRi为i时段下游河道内生态需水流量；Q出境i为河流出境流量，m3/s。水库下泄流量需受到下游河道内生态需水流量和出境流量下限值的约束，与发电出力（由发电水头和发电流量决定）之间形成互馈竞争关系。根据胡波等人［23］提出的生态需水系数—水文参数耦合模型，推求得到澜沧江河道的最小、适宜以及理想的生态需水量分别占实测来水径流量的21%、37%和66%。

4.2 计算结果依据位于景洪水电站上游最邻近的戛旧水文站1961—2000年的实测日流量数据和流域区间雨量站的实测降雨量数据，通过泰森多边形法由区间点雨量资料推求流域面雨量数据［24］，进而通过面雨量数据和流域径流系数［25］，推求得到景洪水电站坝址处断面流量数据。因为澜沧江干流河道落差大，宽窄纵深，水库为河道型水库，将坝址处河道断面流量作为水库天然来水入库流量，对问题的研究影响程度有限，所以在此使用坝址处断面径流量近似作为景洪水库入库流量。

根据实际代表年法，对坝址处40年的径流量序列进行水文频率计算，根据计算结果选取1994.6—1995.5（枯水年，95%）作为枯水典型年，基于该典型年的实际来水情况，在日尺度上对景洪水库进行发电效益与下游河道内生态需水流量-出境流量的完全信息静态博弈模型计算，得到各策略组合的支付函数值计算结果如下表1～3：

表1 景洪水电站枯水典型年发电效益与河道内生态需水—出境流量博弈计算结果

表2 景洪水电站枯水典型年汛期发电效益与河道内生态需水—出境流量博弈计算结果

综上所述，根据纳什均衡准则，对本文计算结果中的景洪水电站发电效益与下游河道内生态需水-出境水博弈策略组合进行检验，得到纳什均衡解如下式（18）～（24）：

表3 景洪水电站枯水典型年非汛期发电效益与河道内生态需水—出境流量博弈计算结果

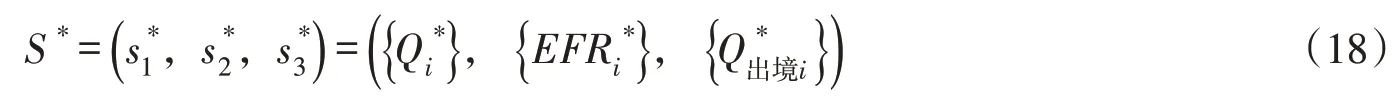
在汛期（6—10月）：

在非汛期（11月—翌年5月）：

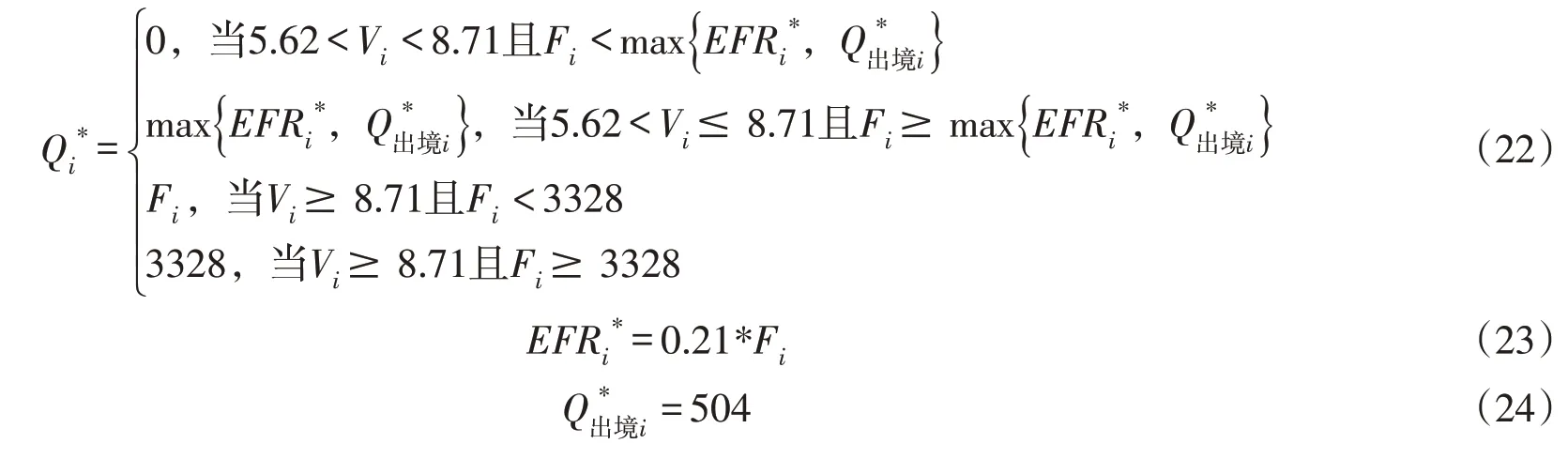
式中：{Qi*}为景洪水电站发电效益的纳什均衡解策略集，m3/s；{EFRi*}为下游河道内生态需水流量约束值的纳什均衡解策略集，为出境需水流量约束值的纳什均衡策略集，m3/s；Vi，为博弈行动时段初的水库库容，亿m3；Fi为入库流量，m3/s。

在枯水典型年来水总量的约束下，景洪水电站发电效益与下游河道内生态需水-出境流量博弈模型纳什均衡解（策略组合1）对应的博弈过程如图1所示。

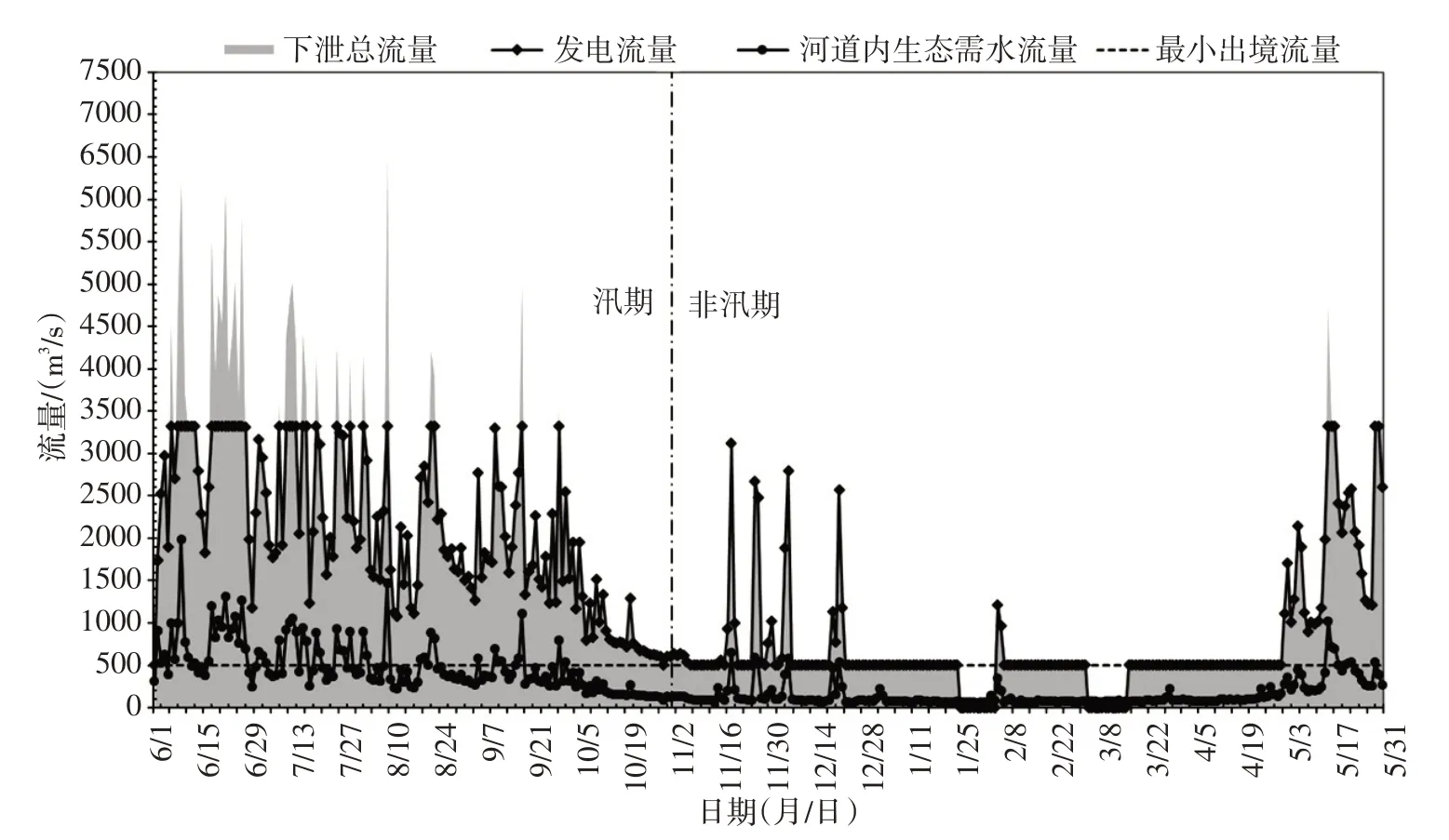
图1 枯水典型年景洪电站发电效益与下游河道内生态需水—出境流量纳什均衡策略博弈过程（策略组合1）

4.3 分析讨论依据上表1～3的计算结果，结合纳什均衡定义，对各参与者的策略组合进行分析可得：

在枯水典型年，水电站发电效益（由发电水头和发电流量决定）与下游河道内生态需水-出境水的博弈竞争关系显著（表1），尤其是在来水量大幅度减少的非汛期（表3）。

（1）在来水量充足的汛期（表2），水电站发电效益与下游河道内生态需水、出境需水的满足程度都比较高，竞争关系不显著。且汛期由于来水量陡涨，景洪水库调节库容有限，不经过水轮机直接下泄的弃水流量在不同的生态需水流量约束值情况下差异不大（图2）。

图2 枯水典型年景洪电站在3种不同博弈策略下的弃水过程

（2）但是在来水量大幅减少的非汛期（表3）情况则大有不同。水库下泄水量伴随枯水年的入库水量减少必然导致水库蓄水量减少、水头降低，进而影响发电效益，尤其是在非汛期（即枯水期），既要考虑水库蓄水以抬高水位，保证后续发电效益，又要尽可能地保障下游河道的生态需水流量和出境流量需求，强调重视河流生态健康与国际河流出境水需求，此时水库发电效益和下游的生态需水-出境流量需求之间的互馈竞争激烈程度显现，并且从图2博弈的弃水过程可以看出，非汛期在策略3，即河道内生态需水约束值取理想值的情境下，未经水轮机直接下泄以满足下游河道内生态需水和出境需水流量的弃水量最大；其次是策略2；而在策略1，即河道内生态需水约束值取最小值的情境下弃水量最小，使水库得以蓄水，在非汛期后期的发电水头和发电流量能够得到更大程度的保障，获得更高的发电效益。

（3）由上表1中依据纳什均衡准则得到的完全信息静态博弈模型支付函数计算结果U可知，景洪水电站枯水典型年发电效益与下游河道内生态需水、出境流量完全信息静态博弈的纳什均衡解为策略组合1，即在满足下游生态需水流量最小值（即天然径流量的21%）的情况下得到景洪水电站发电效益与下游河道内生态需水-出境水博弈的水库优化调配方案，水电站枯水年发电效益达到多年平均发电量的80%，枯水期出境流量不低于504 m3/s 的保证率从常规调度的78.4%（基于下游允景洪水文站2006—2008年的实测数据）提升到93.7%。在此博弈模型计算得到的水库优化调配方案下，景洪水电站枯水典型年发电效益与下游河道内生态需水、出境流量三者的支付函数值最大，总效益值亦为最大。

（4）然而在纳什均衡解中，依旧存在非汛期极枯水时水库安全运行时下泄流量无法满足河流出境流量需求的情况，其中一个关键原因是澜沧江径流主要由雨水补给，降水季节分配不均直接导致澜沧江径流量存在明显的汛期和枯期且径流量差异极大，年最大和最小日均径流量差距可高达10倍［25］，也说明了在澜沧江干流单一水库的调节能力是不够的，梯级水电站的建设将大大提高澜沧江流域水能资源与水量资源的开发利用效率。

5 结论

针对水电开发下河流水资源多目标利用的冲突问题，引入博弈模型，创新性地构建水电站发电效益与下游河道内生态需水—出境流量的完全信息静态博弈模型，以澜沧江干流下游景洪电站为实例，依据纳什均衡准则并耦合支付函数最大化方法进行计算。结果表明：景洪水电站发电效益与下游河道内生态需水-出境需水之间的博弈竞争关系在入库流量大幅减少的非汛期（即枯水期）表现尤为显著，而在水量丰富的汛期表现则稍弱；在枯水典型年来水情况下，当澜沧江下游河道生态需水流量取最小流量约束，即天然径流量的21%时，景洪水电站全年的发电效益（多年平均年发电量的80%）和澜沧江出境流量保证率（93.7%）在该典型年达到最高，综合效益最大化且水库弃水量最小。此外，将本文博弈模型计算结果与传统的调度运行结果进行比较，发现景洪以下河道枯水期的日流量大于504 m3/s（出境流量下限值）、800 m3/s（航运需水下限值）的保证率分别由常规调度下的78.4%、40.3%（基于下游允景洪水文站2006—2008年的实测数据）提高到博弈均衡调度方案下的93.7%和48.8%，说明博弈模型调度方案相较于传统常规调度是存在一定优越性的。

传统水库优化调度有一套成熟的多目标优化方法，但多目标优化方法并未考虑竞争因素之间的博弈关系及其纳什均衡准则，各竞争因素之间的协同性未得到充分体现。本文则充分考虑流域各用水主体间存在的竞争博弈关系，明确针对澜沧江流域在我国境内最下游的景洪水电站为节点，提出发电效益最大化目标与下游河道内生态需水和出境水需求满足程度最高之间的竞争博弈关系，通过定义它们在完全信息静态博弈下的支付函数表达的总效益，给出总效益最大化的发电出力、生态水量和出境水量的保证率，一定程度上克服了传统水库优化调度下各用水竞争要素之间缺乏协同性的缺陷，对于优化流域水库调蓄以协同发电和下游河道内用水综合效益具有借鉴作用。另外，本研究中对澜沧江这类来水量较大且存在明显雨季和旱季的河流，提出了单库在调节水力发电效益与下游河道内用水竞争博弈方面能力较弱的问题，在后续研究中可考虑基于本研究结果，进一步深入分析澜沧江梯级水电站的建设在跨境河流水力发电效益与下游河道内多方用水中的竞争博弈关系，探讨更为合理的水库群优化调度方案。