洪涝灾害三参数损失函数的构建Ⅱ——实例研究

李超超，程晓陶，王艳艳，付德宇

（1.宁夏大学 土木与水利工程学院，宁夏 银川 750021；2.中国水利水电科学研究院，北京 100038；3.宁夏首创海绵城市建设发展有限公司，宁夏 固原 756000）

把握洪涝灾害风险演变规律，是制定城市防洪规划与完善综合风险管理中需研究的科学问题之一。目前关于洪涝灾害风险演变的研究大多难以反映我国城市化进程迅猛发展，不同地区自然地理特征与经济发展水平差异较大的实际情况［1］。本次研究基于上篇中构建的具有物理意义的洪涝灾害损失-重现期风险函数［2］，以太湖流域为例，构建了太湖流域洪涝灾害风险函数；实现了对太湖流域洪涝灾害损失的快速评估与预测；根据风险函数的转折点，对风险进行了分级，可为太湖流域风险管理提供科学依据。

1 研究区域概况

太湖流域是我国城镇化程度最高的流域之一，位于东部长江三角洲，面积36 895 km2。太湖流域属于平原河网地区，围堤密布，降雨丰沛，其河流水系如图1所示。流域地势周边高、中间低，这样的碟状地形不利排水。太湖流域自然条件优越，水陆交通便利，农业生产基本条件好，工业发达，经济基础雄厚，人口稠密。2018年太湖流域年降水量1382 mm，太湖流域总人口6104 万，占全国总人口的4.4%；GDP 87 663 亿元，占全国GDP 的9.7%；人均GDP 14.4 万元，是全国人均GDP的2.2倍［3］。太湖流域降雨、气候、地形、社会经济等方面的特点，导致太湖流域易遭受洪涝灾害且洪灾损失巨大。高度城镇化的太湖流域，“淹不起也淹不得”，对防洪减灾工作的要求不断提高。因此，研究城镇化背景下流域洪涝灾害风险演变规律，对太湖流域洪涝灾害风险管理和流域防洪规划具有重要意义。

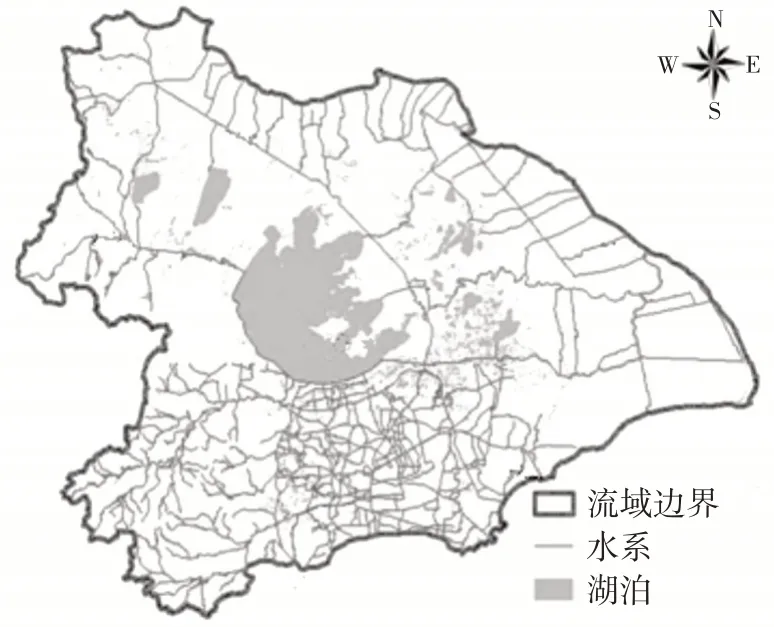
图1 太湖流域水系

2 数据来源

本文引用流域洪水风险情景分析技术研究报告［4］（以下简称“研究报告”）成果中的现状及未来情景下不同频率暴雨的直接经济损失与社会经济数据。以现状条件下的计算结果为数据样本进行拟合。对比曲线拟合的情况并验证模型的合理性，选择拟合效果最佳的S型函数作为预测模型。建立参数与社会经济指标的回归方程，对未来洪涝灾害损失进行预测。

研究报告中太湖流域现状洪水风险分析方案选取的是1999年与2005年实际社会经济数据，降雨采用1999年暴雨为典型的最大30 d 频率为0.001、0.002、0.005、0.01、0.02、0.05、0.1、0.5 的设计降雨。利用SCS CN 法（Soil Conservation Service Curve Number Method）计算净雨，利用VIC 模型（Vari⁃able Infiltration Capacity Model）计算得到上游边界入流［5］。将降雨和入流作为输入，带入大尺度水力学模型（ISIS）计算得到洪水的淹没情况［6-7］。情景设定A2情景和NP 情景，A2情景是IPCC中片面追求经济增长，气候与经济发展模式对洪灾风险管理最不利的情景［8］，NP是符合我国社会经济发展实际情况的国家规划情景。采用降尺度方法对各情景人口和GDP进行预测。最后利用太湖流域洪水风险评估模型（Taihu Basin Risk Assessment System，TBRAS）对不同情景下不同频率的洪涝灾害损失进行评估［9-10］。计算得到1999、2005、2030和2050年不同频率洪灾损失［11］（见表1）。

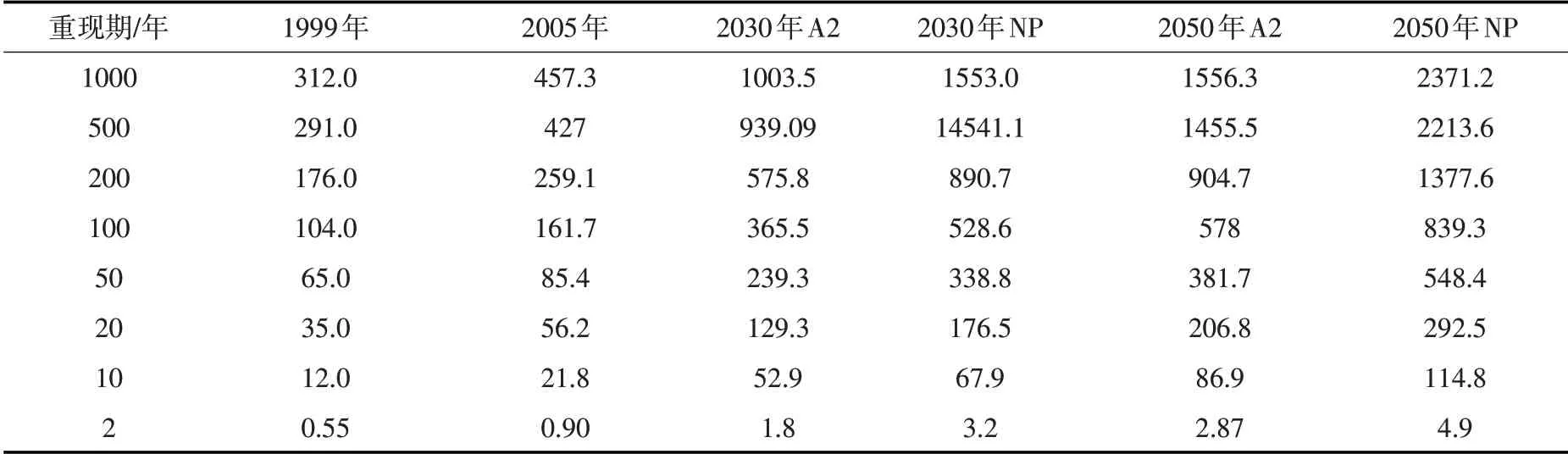
表1 洪灾损失计算结果 （单位：亿元）

3 太湖洪涝灾害风险函数的构建

3.1 损失曲线拟合根据文献［2］选用3种S型损失-重现期函数进行拟合，函数表达式如下：Boltzmann函数：

Logistic函数：

Gompertz函数：

式中：D为洪涝灾害经济损失；R为重现期；Rc为临界重现期；Dc为临界损失；k为区域脆弱性综合指数。

将1999年与2005年数据作为样本进行曲线拟合，拟合结果如表2所示。函数曲线拟合的优劣一般用决定系数R2进行评估，R2越接近1说明函数对拟合值的拟合度越好。

式中：y为待拟合数值；为均值；为拟合值；n为样本数。决定系数R2也称判定系数或者拟合优度。

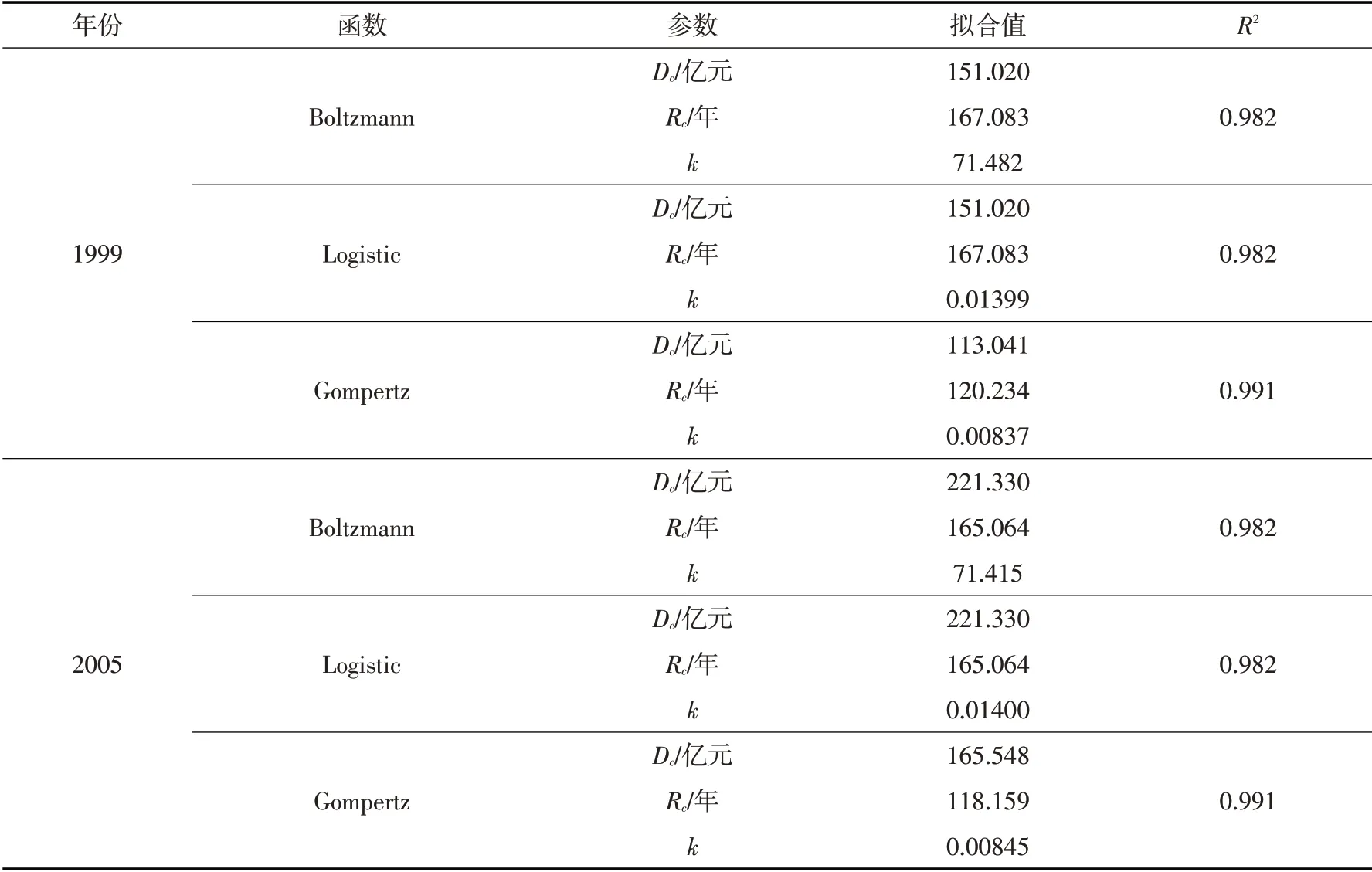
表2 现状情景拟合结果

由表2可知，Boltzmann函数与Logistic函数拟合的Dc值和Rc值一致，k互为倒数。Gompertz拟合的Dc值和Rc均小于前两种函数，函数的拐点出现的相对早，其决定系数R2为0.991，拟合效果最好。因此选用Gompertz函数对模型进行验证。

3.2 模型的验证1931、1954、1983、1991和1999年太湖流域发生了流域大洪水并造成了严重的经济损失［12］。最近的一次流域性洪水发生在2016年。对于暴雨重现期的评估，由于降雨的不均匀性，选择特征时段不同，雨量站点不同，最终的评估结果会存在差异。1999年30 d降雨量相当于150年一遇，2016年30 d降雨量相当于15年一遇［13］。图2为Gompertz拟合的现状情景下的洪涝灾害风险函数曲线。1999年洪涝灾害统计损失为141.25亿元［14］。通过损失-重现期函数计算得到150年一遇洪涝灾害损失值为140.93亿元，模拟值与实际值相差-0.23%。

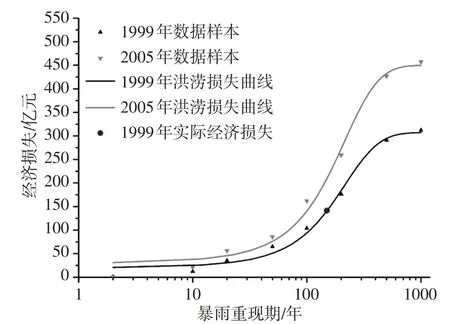
图2 现状情景下洪涝灾害损失-重现期函数的验证

2016年太湖流域受超强厄尔尼诺现象影响发生超标准洪水，造成洪灾经济损失75.28亿元［15］。以1999年和2005年模拟结果为基准，根据GDP 对Dc值进行线性插值，2016年太湖流域GDP 为72 779亿元，得到Dc=381，其他参数取均值：Rc=119，k=0.0084。计算得到15年一遇洪涝灾害损失值为94.45亿元，模拟值较实际值偏大，主要原因是构建2016年损失-重现期函数时，仅考虑了社会经济增长，对Dc进行了调整，其他参数保持不变。自1999年流域大洪水后，太湖流域骨干工程相继建成，流域洪水调度方式也逐步优化，流域防御能力大为提高［16］。从验证结果来看，现状情景下损失-重现期曲线对经济损失的评估是合理的。

4 太湖洪涝灾害风险函数的应用

4.1 风险预测洪涝灾害损失-重现期曲线还可应用于未来流域洪灾损失预测。以表1中的未来A2与NP 情景下洪灾损失数据为样本，采用Gompertz 模型进行曲线拟合，拟合结果见图3和图4，主要结果见表3。由表3可知，未来情景曲线拟合的决定系数R2约为0.99，说明暴雨洪涝损失-重现期曲线与样本拟合效果较好。

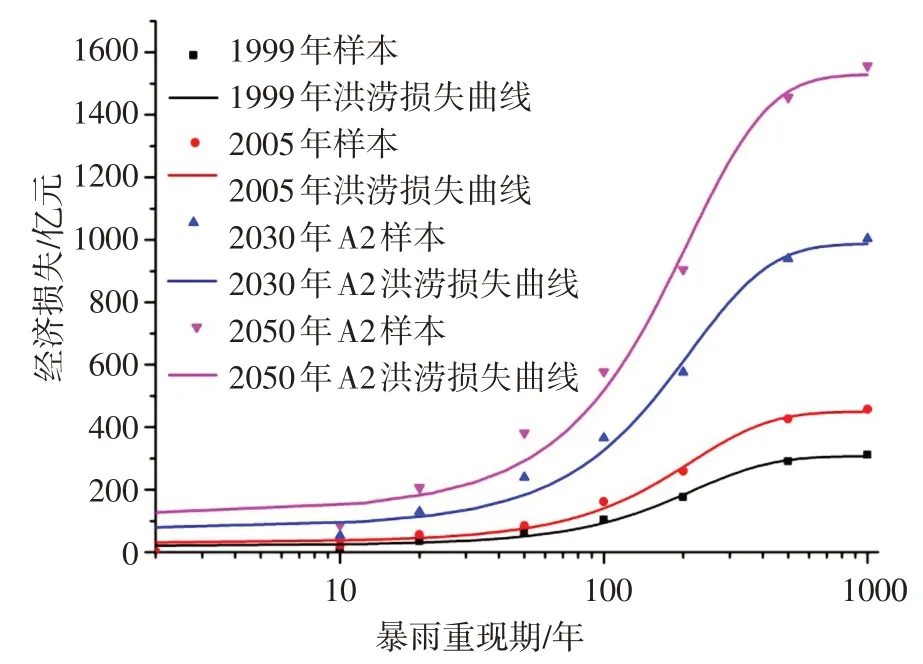
图3 A2情景下洪涝灾害损失-重现期函数

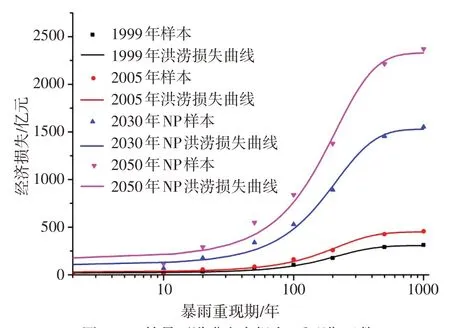
图4 NP情景下洪涝灾害损失-重现期函数

表3 未来情景拟合结果

研究报告中情景设定，主要是社会经济参数的变化。根据表2和表3，对比1999、2005、2030与2050年拟合参数值，可知Rc与k变化较小，Dc变化较大，说明临界损失Dc是与社会经济相关的参数。因此建立临界损失Dc与GDP的相关关系，如图5和图6所示，两者线性相关。

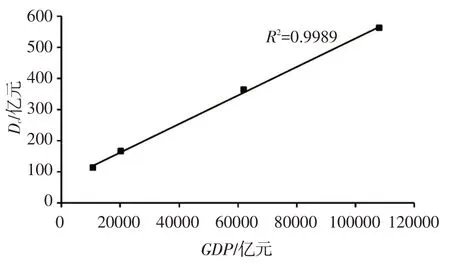
图5 A2情景下Dc与GDP的相关关系

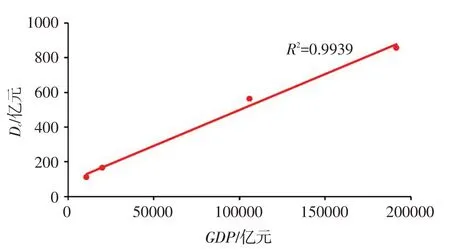
图6 NP情景下Dc与GDP的相关关系

2018年太湖流域GDP 为87 663 亿元，研究报告采用降尺度方法预测NP 情景下2020年GDP 为63 265 亿元，预测值与实际值偏差较大，因此对GDP 预测数据进行调整。图7为太湖流域2003—2018年度太湖流域GDP统计数据［3］，其增长率变动较大，近5年的GDP平均增长率为8.64%。太湖流域经济预测采用指数函数进行预测，增长率按8.64%计算，GDP 预测结果见表4。根据建立的NP 情景下Dc与GDP相关关系和预测GDP值，即可对Dc数据进行扩展。

表4 预测GDP与扩展的Dc值

求得所有方案拟合参数平均值：Rc=115，k=0.0085，结合扩展的Dc数据，即预测太湖流域未来洪涝灾害损失。2020—2040年太湖流域洪涝灾害相对损失（损失/GDP）-重现期曲线如图8所示。未来20年，太湖流域百年一遇的暴雨洪涝灾害相对损失约为0.3%～0.5%，千年一遇的暴雨洪涝灾害相对经济损失约为1.1%～1.4%。

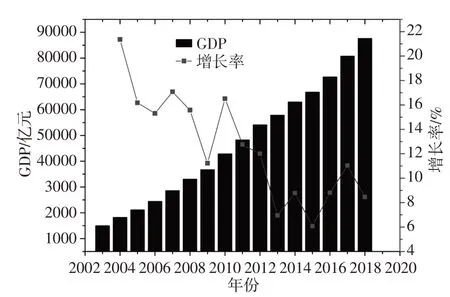
图7 2003—2018年太湖流域GDP统计

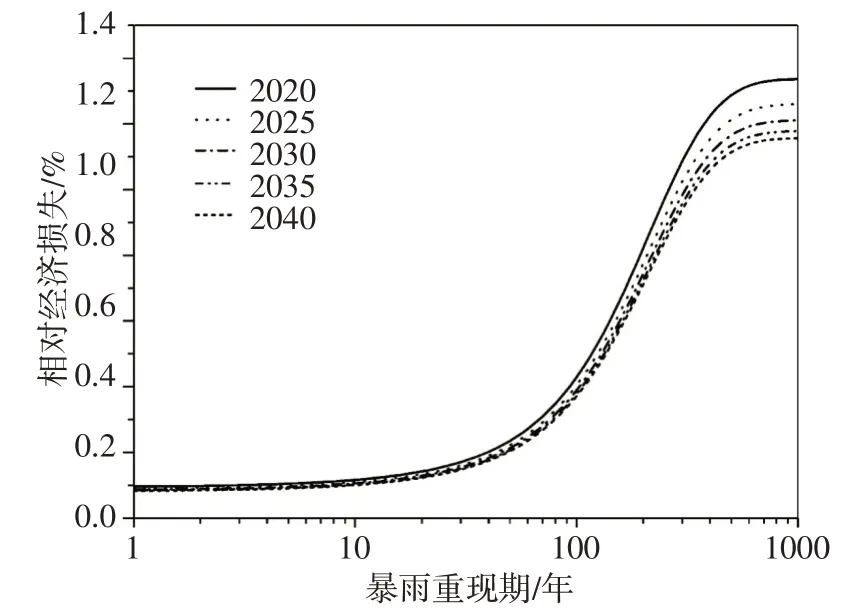
图8 太湖流域洪涝灾害风险预测

4.2 风险演变趋势分析以社会经济增长、防洪工程标准提高、区域综合脆弱性变化为驱动因素，分析太湖流域未来洪涝灾害风险的演变趋势。假设1999年为基准，将1999年太湖流域风险函数曲线设定为基准风险函数曲线S1：

以2005年太湖流域风险函数曲线作为经济发展曲线S2：

临界损失Dc从112.6亿元增长到165.5亿元，由于城市化洪涝灾害风险增长了46.9%。同理，A2情景下2030—2050年洪涝灾害风险将会增长55.5%，NP情景下2030—2050年洪涝灾害风险将会增长53.1%。随着城市化进程的推进，洪灾风险会持续增长，社会经济因素的影响会逐渐增强，NP情景洪灾风险的增长率低于A2情景。

假设由于防洪工程体系的完善，流域的防灾能力增强，综合防洪标准提高一倍，临界重现期Rc从115年一遇增长到230年一遇。防洪能力增长曲线S3为：

由于防洪标准提高，降低的洪涝灾害风险如图9中阴影部分所示，洪灾风险会降低14.54%。评估防洪工程标准的合理性，一般需要计算投资效益比。仅从本文的研究结果出发，一再提高防洪标准，加大防洪工程投入，不一定能大幅度降低风险。太湖流域洪涝灾害风险函数的临界重现期Rc为115年，该点是风险急速增长的转折点，以此作为太湖流域防御阈值，推荐防洪标准为115年。根据太湖流域防洪规划，到2025年流域防洪标准达到防御不同降雨典型年的100年一遇标准，遇1999年实况洪水，能确保流域重点保护对象防洪安全。规划防洪标准与临界重现期相近，说明S型三参数洪涝灾害风险函数曲线可为流域防洪标准的制定提供一定科学依据。

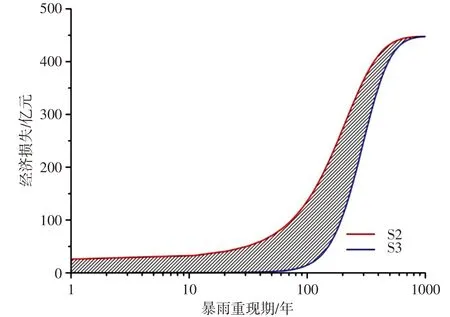
图9 防洪排涝工程标准提高对洪灾风险的影响

假设由于防洪工程保护，高风险区被开发，原来易受淹地区放松了防范，承灾体的脆弱性反而凸显。突变性增强曲线S4为：

综合脆弱性指数从0.0085增长到0.017。如图10所示，S3与S4的交点为（Ri，Di）。重现期在Ri之内，洪涝灾害风险会降低，如图中阴影部分1所示，风险会降低48.1%。重现期超过Ri时，风险会增长，如图中阴影部分2所示，风险会增加6.7%。由于防洪工程的保护，防洪标准内洪涝灾害损失有效降低。超标准洪涝发生的概率较小，人们容易缺乏风险意识与应对经验，风险防范准备不足，加之下垫面变化及现代社会正常运转对生命线系统的高度依赖，导致流域综合脆弱性增大，一旦发生超标准暴雨洪涝，灾害影响范围远超出受淹范围，损失会急剧上升，呈现出突变特征。流域综合脆弱性指数越大，这种突变性就越强。

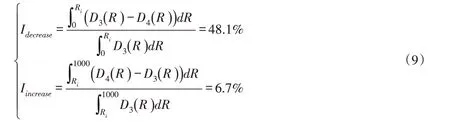
4.3 风险分级与减灾对策制定如图11所示，D2（R）为太湖流域2005年洪灾风险函数，D′2(R)和D2（2）（R）分别是它的一阶导函数和二阶导函数，临界重现期Rc=115年一遇。在防洪标准制定时，设计重现期一般采用10的整数倍，因此取Ra≈10年，Rc≈100年，Rb≈200年。转折点A、B与C可将洪涝灾害分为4个区间：Ⅰ、Ⅱ、Ⅲ和Ⅴ区间，分别对应小、中、大和特大风险级别。不同风险级别，应采取不同减灾对策。当暴雨重现期小于临界重现期Rc时，控制性措施占主导，加强防御性（Resistance）能力建设，当暴雨重现期大于临界重现期Rc时，受淹不可避免，需要加强恢复性（Resilience）能力建设［17］。

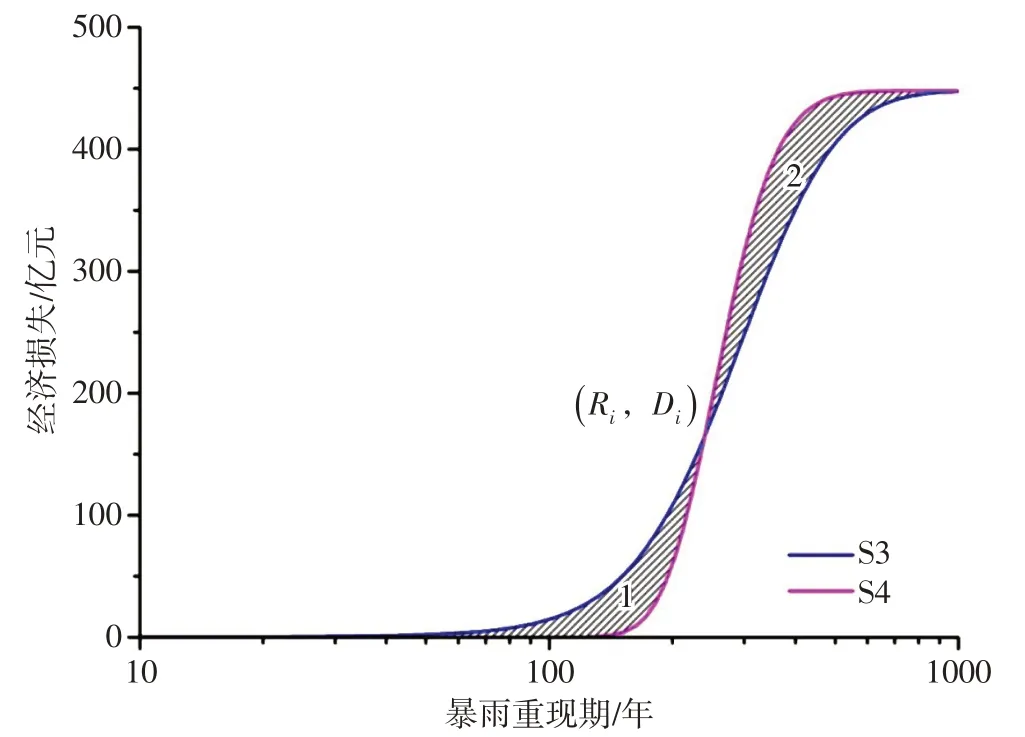
图10 承灾体脆弱性增强对洪灾风险的影响

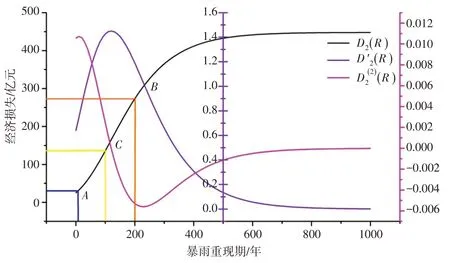
图11 太湖流域洪灾风险函数及其导函数

根据太湖流域洪涝灾害风险的预测结果，未来太湖流域的洪涝灾害风险仍旧会增长。现有的防洪工程措施的防灾减灾效益有限，需要制定流域综合性防洪减灾对策。根据风险分级的结果，可得出以下结论：

（1）太湖流域2005年风险函数曲线，识别出的太湖流域风险管理的适度防御阈值为100年一遇。重现期小于100年一遇的暴雨，属于中、小风险级别，主要采用防御性措施。根据太湖流域防洪规划，到2025年流域防洪标准达到防御不同降雨典型年的100年一遇标准。规划防洪标准与临界重现期相近，说明S型三参数洪涝灾害风险函数曲线可为流域或区域（城市）规划防洪标准的制定提供一定科学依据。洪涝灾害风险函数识别出的适度防御阈值可为制定防洪标准中“度”的把握提供一种新思路和新方法。

（2）太湖流域超100年一遇的暴雨，属于大风险级别，超200年一遇的暴雨，属于特大风险级别。防御超标准洪涝灾害，需要加强恢复性能力建设。例如：加强防汛预警系统建设；加强流域洪水风险区管理，根据风险区划结果，规范洪水高风险区内人的防洪行为、开发行为和减轻或缓解洪水灾害发生后的影响；重视洪水保险制度的研究与建立等。

5 结论

在城市化程度加深、社会经济增长、防洪工程标准提高背景下，流域暴雨洪涝灾害风险的演变趋势发生变化，洪灾风险的评估与预测应考虑这些因素，并根据这种变化对洪水风险管理策略与规划做出相应调整。本文构建了太湖流域暴雨洪涝损失-重现期S型三参数曲线，得出如下结论：

（1）三参数洪涝灾害损失-重现期函数曲线可较好地反映洪灾风险演变规律，可作为流域洪涝灾害损失快速评估和预测一种有效方法。风险函数的转折点，可作为制定适度防御阈值和风险分级的依据。模型能够反映城市化、社会经济增长、防洪标准提高情况下，流域洪涝灾害风险的演变趋势。该方法的应用不局限于流域尺度，也可以应用于国家、城市、社区等多尺度的洪涝灾害风险评估、预测与分级。

（2）由于历史洪涝灾害数据的限制，模型仅用1999年和2016年洪灾数据做了验证。临界损失Dc与经济指标GDP 的相关关系，临界重现期Rc与流域综合防洪标准的相关关系已在本研究中得到论证。区域综合脆弱性指数k有待进一步研究，它可以反映洪涝灾害损失突变性特点。脆弱性受自然、社会、经济、环境、政策和制度等多方面影响，具有多维度的特点，首先要选择指标，然后进行分类并确定权重，评估出一个综合指标，最终才能建立区域综合脆弱性指数k与这个综合指标的相关关系。

（3）模型建立的数据样本是通过水文、水力学模型、损失评估模型对不同频率的暴雨进行数值模拟得到的。本文所构建模型数据基于VIC 模型、大尺度水力学模型ISIS 和洪水风险评估模型TBRAS，以上模型中主要参数均对损失函数计算精度产生影响。未来可以通过提高这些模型的精度，模拟出更精确的数据来完善损失-重现期函数模型。