中速磁浮列车靴轨动力学分析与试验研究

李 烨，曾杰伟，向湘林

(1.湖南磁浮技术研究中心有限公司，长沙 410000 2.国防科学技术大学 智能科学学院，长沙 410000)

0 引 言

作为一种新型城市轨道交通工具，磁浮列车以其独特的技术优势，如爬坡能力强、转弯半径下、振动噪声低等，在城市化发展过程中扮演着至关重要的角色，具备十分广阔的发展潜力[1]。

现有轨道交通车辆的供电模式主要有接触网模式和接触轨模式。其中接触轨模式需要沿列车行进方向设置专门的供电轨道(即接触轨)，同时在列车侧部设置专门的取电装置(即受电靴)，列车行进过程中通过受电靴与接触轨之间保持接触从而实现列车电能的获取[2]。与架空接触网制式相比，接触轨供电模式耐磨性能更优，且对城市景观干扰较小，基于上述原因，目前国内的中低速磁浮运营线或试验线均采用侧部接触轨供电模式。

国内外众多学者对城市轨道交通列车靴轨耦合特性开展了研究。王瑞[3]以地铁车辆为研究对象，基于非线性赫兹接触理论对地铁接触轨供电系统的靴轨垂向耦合动力学进行了研究与评价；李宁等[4]比较了中低速磁浮交通的3种受流模式，并提出一种新型的侧向受电靴设计方案；李国富[5]针对地铁接触轨系统建立了刚柔耦合动力学模型并开展耦合分析，探讨了各种影响元素对受流效果的影响。

综上所述，就接触轨供电模式而言，受电靴与接触轨之间的良好接触及受流稳定是车辆供电正常和运行安全的必要保证[6-8]。目前针对靴轨耦合的特性研究大多集中在轮轨领域，对于磁浮列车侧部受流靴轨关系的相关研究较少，因此开展磁浮列车靴轨耦合特性的研究十分必要。本文借助ANSYS针对中速磁浮列车受电靴与接触轨之间的耦合动力学特性开展研究，结合试验对耦合模型进行验证，在此基础上分析了接触轨跨距和运行速度对靴轨耦合动力学性能，为中速磁浮靴轨优化设计提供参考。

1 计算模型

1.1 受电靴动力仿真模型

磁浮列车受电靴为四连杆结构，通过弹簧提供静态接触力，弹簧设置一定的刚度，见图1。将受电靴的主要结构等效为刚体，关节位置采用合适的铰链连接。受电靴滑板通过滑板托架限制其摆动角度。本文计算中所设定的受电靴提供的静态接触力为100 N。

利用ANSYS进行受电靴的动态运动仿真，模拟受电靴的上升运动过程。在受电弓自由上升的运动过程中，滑板在空间中的运行轨迹由z方向和x方向的坐标值合成，见图2。滑板的运行轨迹是一条近似抛物线的曲线。

图1 受电靴三维模型Fig.1 3D model of current collector

图2 受电靴升高过程中滑板纵向与垂向位移Fig.2 Longitudinal and vertical displacement during the lift of carbon slide of shoegear

1.2 接触轨动力学仿真模型

磁浮列车使用的接触轨为钢铝复合轨，根据截面基本形状分为工型和C型，接触表面为钢带，本体为铝合金。本文将接触轨的材料简化为铝合金，并在两个接触轨锚段之间设置膨胀接头，膨胀接头接缝宽度为100 mm。工型和C型接触轨模型分别见图3和图4。

接触轨的截面相对线路长度较小，接触轨的形变不能被忽略，故将接触轨考虑为梁。接触轨的锚段长度约为50 m，标称跨距为2、2.5、3 m。接触轨的模型中每间隔一个跨距有一个固定点，固定点用于模拟轨道的绝缘支撑点，固定点用弹簧等效。

图3 工型轨有限元模型Fig.3 Finite element model of H-section rail

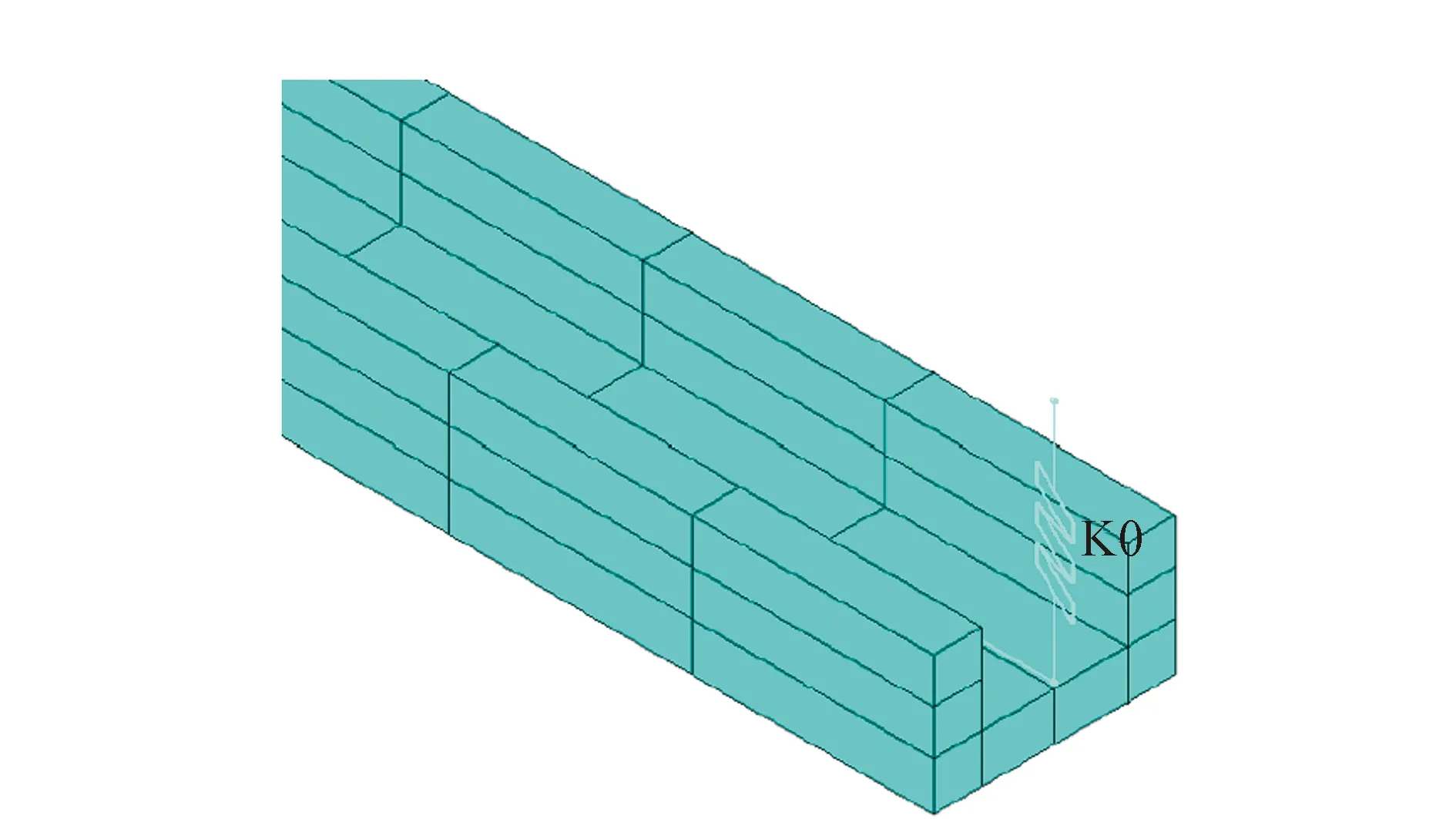
图4 C型轨有限元模型Fig.4 Finite element model of C-section rail

图5 受电靴与接触轨的耦合仿真模型Fig.5 Coupling simulation model of shoegear and conductor rail

1.3 靴轨动力仿真模型

受电靴在运动过程中与接触轨之间的作用方式为滑动摩擦，靴轨相互作用过程采用刚柔耦合计算模式。使用罚函数法计算受电靴与接触轨的接触效应，接触面为滑板表面，目标面为接触轨表面，见图5。

2 计算模型的试验验证

为了验证仿真模型和计算方法的可靠性，将仿真计算结果与中速靴轨耦合动态试验数据进行对比分析，针对耦合模型进行验证。

2.1 靴轨耦合试验工况

中速靴轨耦合试验的试验对象为160 km/h的中速磁浮列车研发的中速工型接触轨，采用受电靴在环形工型接触轨转盘上运动的方式开展靴轨耦合试验，最高速度为160 km/h。试验现场见图6。

图6 转盘试验安装现场Fig.6 Test equipments installation of turntable in test site

2.2 计算模型的试验验证

试验针对靴轨耦合过程的受电靴碳滑板的垂向加速度、靴轨动态位移等重要参数进行了测试。试验所得耦合振动加速度变化曲线见图7。

为了尽可能真实地模拟试验工况，建立了相应的受电靴及环形工型轨模型，相关计算参数(靴轨初始接触力等)与试验条件保持一致，计算所得的靴头振动加速度曲线见图8。

图7 160 km/h靴轨耦合试验加速度曲线Fig.7 Vibration acceleration curve of coupling of experiment(160 km/h)

图8 160 km/h靴轨耦合仿真加速度曲线Fig.8 Vibration acceleration curve of coupling of simulation(160 km/h)

由图7和图8可见，试验和仿真结果对应的振动加速度均在±6 g范围内变化，二者加速度幅值十分接近，曲线吻合较好，验证了计算模型的可靠性。

3 接触轨跨距对靴轨动力学性能影响分析

3.1 工型接触轨不同跨距下动力学仿真分析

3.1.1 仿真工况

仿真计算工况设置的受电靴运行速度为160 km/h，接触轨的锚段长度为50 m，接触轨跨距设置为2、2.5、3 m，轨道截面类型为工型轨，轨道中间设置有带断口的膨胀接头，重点计算中速条件下靴轨动态接触压力的变化情况。

3.1.2 结果及分析

受电靴以160 km/h通过不同跨距的接触轨得到靴轨接触压力变化的对比曲线见图9。由图9可见，不同跨距下接触力在膨胀接头处均出现较大的变化，说明受电靴通过膨胀接头时均有较大的振动，且振动持续一段距离后衰减。由图9(a)可见，在轨道区段内2.5 m跨距与2 m跨距下接触力整体相差不大，且动态接触力峰值而言在2 m跨距下更大；由图9(b)可见，2.5 m跨距下动态接触力的变化幅度整体低于跨距在3 m时的情况，就动态接触力的波动情况而言，跨距在2.5 m时的靴轨受流状态最佳。

为了比较不同跨距下的靴轨受流质量，统计了两段接触轨连续区段(不含膨胀接头)不同跨距下的接触力的相关参数值，见表1。相关统计参数主要包括接触力最值以及标准差，其中标准差作为最直接的关键指标可以直接反应靴轨之间的受流质量。

表1中的25～45 m区段位于膨胀接头前，55～80 m区段位于膨胀接头后。通过统计数据可见，随着跨距的增加接头前区段接触力标准差差别较小，但接头后区段的接触力标准差随着跨距的增加逐渐增大，说明接头后区段随着跨距的增大接触力波动变大，受流质量相比接头前区段有所降低。

同时结合图9可见，在中心锚节与膨胀接头之间的区段接触力变化幅值较小，说明中心锚结至接头段的振动较弱，但是受电靴通过膨胀接头后的振动较强。膨胀接头后的区段的振动可以传递至中心锚结，且该区域的振动强弱与跨距长度有关，跨距小，接触轨传递振动衰减较快，跨距大，接触轨传递振动衰减较慢。

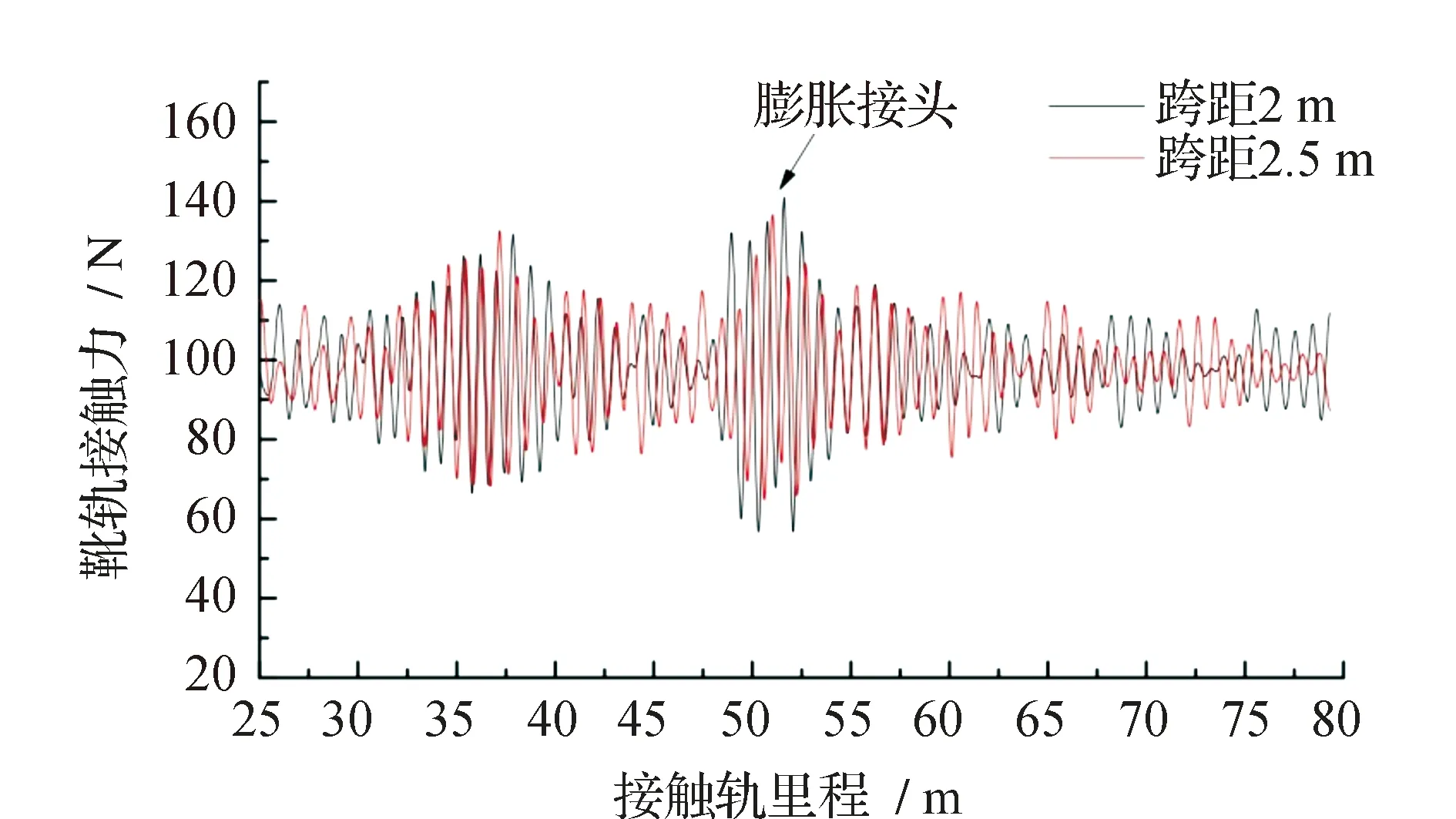
(a)2 m和2.5 m跨距对比

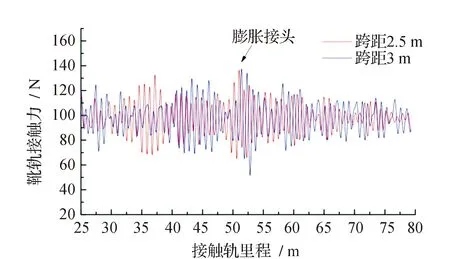
(b)2.5 m和3 m跨距对比

(c)3种跨距对比图9 不同跨距下动态接触力时程曲线(工型轨)Fig.9 Curves of dynamic ontact force at different time course (H-section rail)

表1 不同跨距不含膨胀接头接触力统计值(工型轨)

前后两个半锚段接触轨区域(含膨胀接头)的接触力特征参数值见表2。由表2可见，相同初始压力下2.5 m跨距时的靴轨动态接触力标准差最小，即跨距在2.5 m时的靴轨接触力的离散程度最小，受流质量最好，在3种跨距中最佳。

表2 不同跨距含膨胀接头接触力统计值(工型轨)

图10 不同跨距下动态接触力时程曲线(C型轨)Fig.10 Curves of dynamic contact force at different time course(C-section rail)

综合以上分析可见，从靴轨接触的动力学性能出发，2.5 m跨距时所对应的靴轨受流质量最佳，其产生的系统振动或磨损最小。但3种跨距的靴轨接触力差距不大，均适应中速磁浮列车的要求，但考虑到磁浮交通线路较长，缩小接触轨绝缘支撑间距会增加大量的绝缘支撑座及其附件，增加一定的建设成本，因此从经济性的角度考虑，3 m的跨距具备更强的工程适用性。

3.2 C型接触轨不同跨距仿真分析

3.2.1 仿真工况

仿真工况与工型轨类似，设置的受电靴运行速度为160 km/h，接触轨的锚段长度为50 m，接触轨跨距设置为2、2.5、3 m，轨道截面类型为C型轨，轨道中间设置有带断口的膨胀接头，重点计算中速条件下靴轨动态接触压力的变化情况。

3.2.2 结果及分析

通过开展受电靴以160 km/h通过不同跨距的C型接触轨区段，并得到靴轨动态接触力时间历程曲线，见图10。

由图10可见，3条曲线中接触力在膨胀接头位置处均出现较大的波动，说明受电靴通过接触轨膨胀接头时产生很明显的振动，且振动持续一段距离才衰减。对比图10各曲线可见，2.5 m跨距时接触力的整体变化幅度明显低于另外两种跨距，其中2 m跨距下接触力波动最剧烈，即2.5 m跨距下受流质量较好。

不同跨距下不含有膨胀接头区段的接触力的相关参数见表3。与表1类似，表中25～50 m是锚段关节前的中间跨，55～80 m是锚段关节后的中间跨。通过对比接触力标准差可见跨距与标准差之间不存在严格的正相关关系，即C型轨条件下接触力变化不随着跨距线性变化。

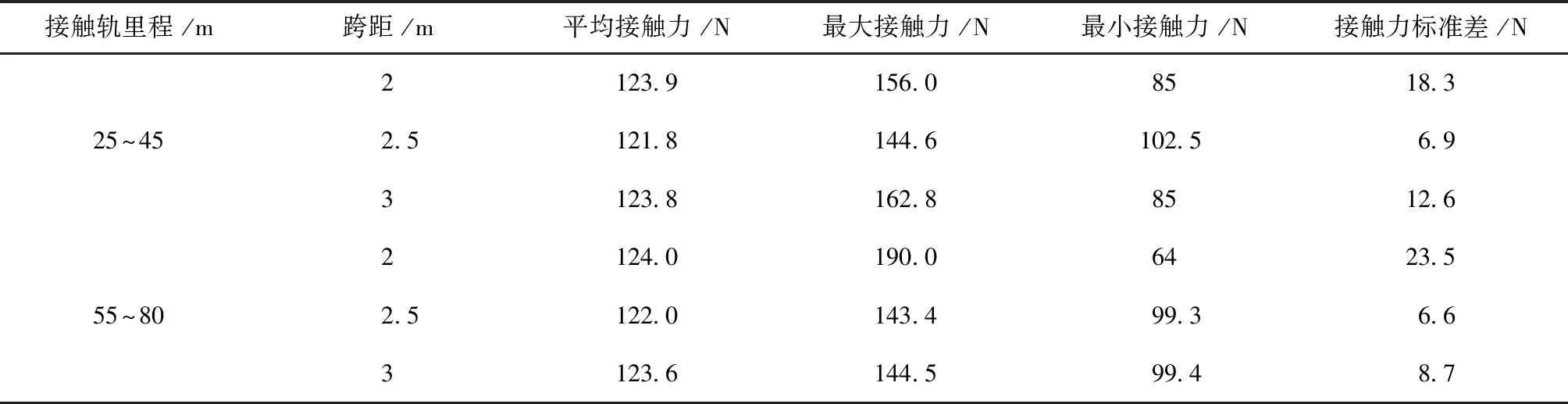
表3 不同跨距不含膨胀接头接触力统计值(C型轨)

不同跨距含膨胀接头的靴轨接触力参数见表4，相同速度等级下2 m跨距时的接触力标准差最大，说明2 m跨距时靴轨接触力离散程度最高，在3种跨距中受流质量最差。

综上所述，跨距为2.5 m时靴轨受流质量最优，但3种跨距的靴轨接触力均满足160 km/h的要求，在综合了经济性与靴轨匹配性等多种因素后可见，2.5 m跨距具备更好的实用性能。

4 运行速度对靴轨动力学性能影响分析

4.1 工型接触轨不同运行速度下动力学仿真分析

4.1.1 仿真工况

受电靴速度设置为80～160 km/h，锚段长度设置为50 m、采用2.5 m跨距的工型接触轨，接触轨区间带膨胀接头，通过开展受电靴与接触轨的动力学计算，得到相关靴轨的动态响应。

4.1.2 结果及分析

为了分析靴轨耦合接触力与速度之间的关系，给出了不同速度状态下受电靴与接触轨之间的耦合接触力的变化曲线，见图11。

由图11可见，受电靴经过膨胀接头时接触轨出现剧烈波动，且其波动幅度随着速度的提高迅速增大，且在高速条件下需要更长的运行距离用来衰减因膨胀接头造成的接触力突变。同时，随着速度的提高，运行过程中的动态接触力的变化幅度整体呈现变大的趋势。

不同速度等级下接触力标准差的统计值见表5。由表5可见，随着运行速度的增加，接触力标准差整体增大，即靴轨接触力的变化随着运行速度的增加而更加剧烈。但当速度140 km/h时标准差出现下降，即说明在现有工况条件下运行速度140 km/h时具备最佳的受流质量和靴轨动力学性能。且80～160 km/h对应所有工况下接触力均大于零，没有出现离线情况。

表5 不同速度下接触力统计值(工型轨)

表4 不同跨距含膨胀接头接触力统计值(C型轨)

图11 不同运行速度下动态接触力曲线(工型轨)Fig.11 Curves of dynamic contact force at different velocity(H-section rail)

图12 不同运行速度下动态接触力曲线(C型轨)Fig.12 Curves of dynamic contact force at different velocity(C-section rail)

4.2 C型接触轨不同运行速度下动力学仿真分析

4.2.1 仿真工况

与工型轨类似，受电靴速度区间设置为80～160 km/h，锚段长度设置为50 m、采用2.5 m跨距的C型接触轨，接触轨区间带膨胀接头。

4.2.2 结果及分析

不同速度状态下受电靴与接触轨之间的耦合接触力的变化曲线见图12。

由图12可见，与工型轨类似，受电靴经过接触轨膨胀接头时会出现剧烈波动，其波动幅度随着速度提高迅速增大，但其接触力突变的衰减过程相比工型轨较为迅速。同时结合图11可见，受电靴经过工型轨膨胀接头产生的接触力峰值略大于C型接触轨。

受电靴在不同速度下经过C型轨的接触力统计参数见表6。由表6可见，随着速度的增加，接触力标准差也是逐渐增大的，且标准差数值整体低于同等速度条件下的工型轨对应的状态。且80～160 km/h对应所有工况下接触力均大于零，没有出现离线情况。

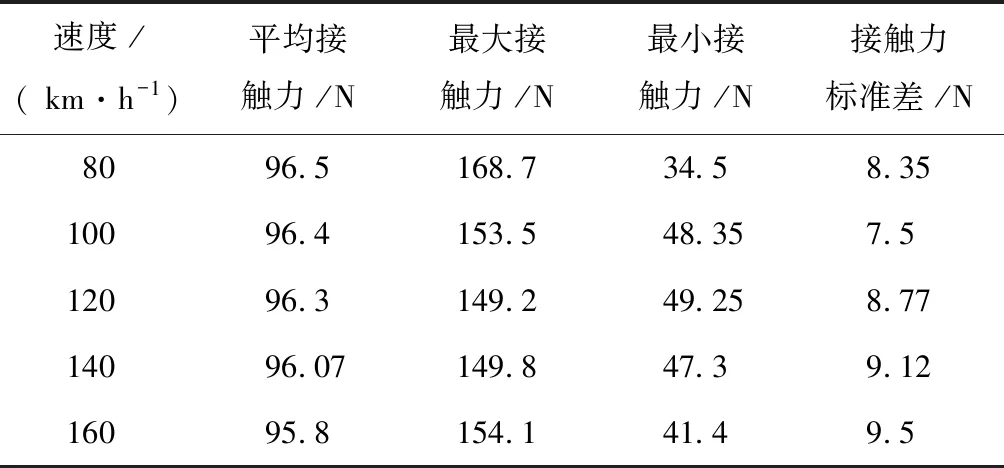
表6 不同速度下接触力统计值(C型轨)

5 结 论

本文基于ANSYS开展了靴轨耦合动力学计算及分析，综合中速靴轨关系试验得到如下结论：

1)在本文仿真工况下，受电靴通过接触轨膨胀接头时均有较大的振动，且振动持续一段距离后衰减，且同等条件下工型轨需要的衰减距离更长。

2)在相同外界条件下，对工型轨而言2.5 m跨距时接触力标准差最小即受流质量最好，但与3 m跨距时相差不大，考虑到经济性因素选用3 m跨距更符合实用性；对C型轨而言2.5 m跨距时接触力的变化幅度明显低于另外两种跨距，即2.5 m跨距下受流质量较好。

3)随着速度的提高，运行过程中两种轨型的动态接触力的变化幅度均整体呈现变大的趋势。