不等式

一、填空题

1.已知集合M=｛a，0｝，N=｛x|2x2-3x＜0，x∈Z｝，如果M∩N≠∅，则a=________.

2.（2019年全国卷Ⅱ改编）设集合A=｛x|x2-5x+6＞0｝，B=｛x|x-1＜0｝，则A∩B=________.

3.已知实数x，y满足则目标函数z=x-y的最小值为________.

4.已知a＞b＞1且2logab+3logba=7，则的最小值为________.

5.某单位用32000元购买了一台实验仪器，假设这台仪器从启用的第一天起连续使用，第n天的维修保养费为元，若使这台仪器的日平均费用最少，则一共应使用________天.

6.（2019年淮安模拟）若对任意实数p∈[-1，1]，不等式px2+（p-3）x-3＞0成立，则实数x的取值范围为________.

7.（2019年无锡调研）若正数a，b满足a+b=2，则的最小值是________.

8.若不等式bx+c+9lnx≤x2对任意的x∈（0，+∞），b∈（0，3）恒成立，则实数c的取值范围是________.

10.实数x，y满足2-cos2（2x+3y-1），则5x2-2y的最小值是________.

二、解答题

11.如图所示，A，B是两个垃圾中转站，B在A的正东方向16km处，直线AB的南面为居民生活区.为了妥善处理生活垃圾，政府决定在AB的北面建一个垃圾发电厂P.垃圾发电厂P的选址拟满足以下两个要求（A，B，P可看成三个点）：①垃圾发电厂到两个垃圾中转站的距离与它们每天集中的生活垃圾量成反比，比例系数相同；②垃圾发电厂应尽量远离居民区（这里参考的指标是点P到直线AB的距离要尽可能大）.现估测得A，B两个中转站每天集中的生活垃圾量分别约为30t和50t，问垃圾发电厂该如何选址才能同时满足上述要求？

（第11题）

12.（2020年武汉市调研）某地需要修建一条大型输油管道通过240km 宽的沙漠地带，该段输油管道两端的输油站已建好，余下工程是在该段两端已建好的输油站之间铺设输油管道和等距离修建增压站（又称泵站）.经预算，修建一个增压站的费用为400万元，铺设距离为xkm 的相邻两增压站之间的输油管道的费用为（x2+x）万元.设余下工程的总费用为y万元.

（1）试将y表示成x的函数；

（2）需要修建多少个增压站才能使y最小，其最小值为多少？

13.某中学校园内原有一块四分之一圆面形状的草坪AMN（如图1），其中AM=AN=8m，∠MAN=90°.今年暑假整治校园环境时，为美观起见，学校拟将原有草坪扩大，具体实施方案是：从圆弧上一点P作圆弧的切线BD，分别与AM，AN的延长线交于B，D，并以AB，AD为邻边构造矩形ABCD，再以C为圆心制作一块与AMN形状相同的草坪，构成矩形绿地ABCD（如图2）.

（1）求矩形绿地ABCD占地面积的最小值；

（2）若由于地形条件限制，使得矩形一边AB的长度不能超过10m，求此时矩形绿地ABCD占地面积的最小值.

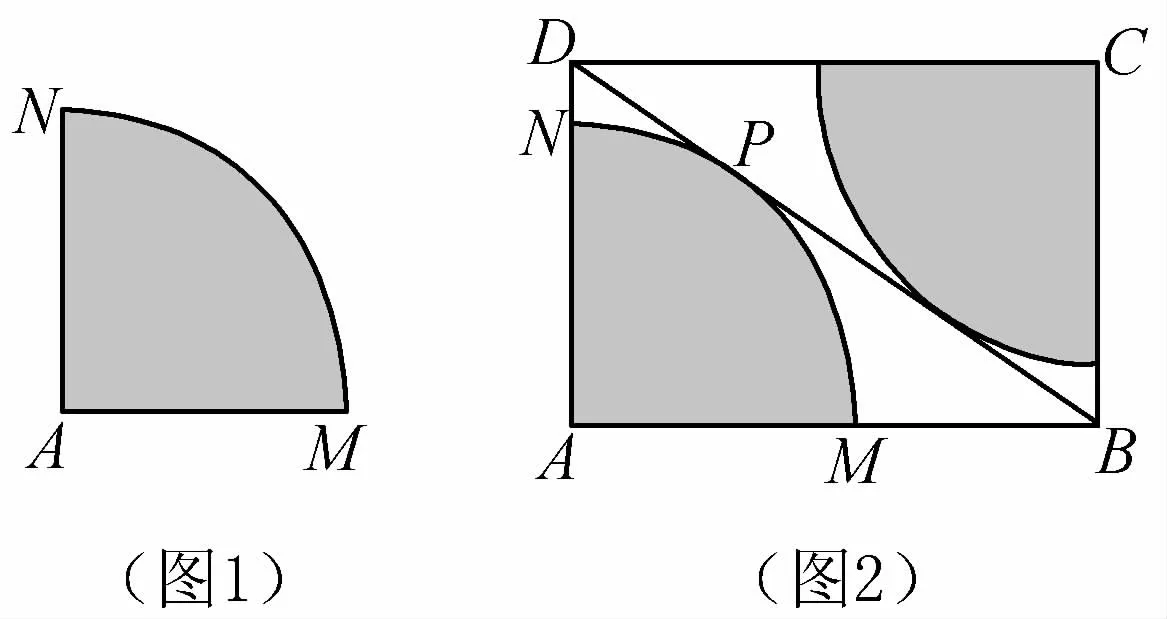
（第13题）

14.已知函数f（x）=2lnx+x-ax2，g（x）=x（lnx-3）+（1-a）x2.

（1）若函数f（x）在区间[1，4]上单调递增，求实数a的取值范围；

（2）若曲线g（x）在x=e处的切线平行于直线x+y=0，求证：对∀x∈（0，+∞），.