具有相位补偿的改进log-MMSE语音增强算法

阮振裔，王 涛，石超宇

(上海大学 通信与信息工程学院，上海 200444)

1 引言

语音增强的作用是提高受损语音的质量和可懂度[1]。于现实中采集到的语音信号往往伴有周围的环境噪声，人声干扰以及其他因素的影响。在许多语音系统如语音通信，语音识别中都需要使用到语音增强算法来提升系统的性能。

根据麦克风的数量进行分类，可以把语音增强算法分为单通道(单麦克风)语音增强和多通道(多麦克风或麦克风阵列)语音增强。本文所研究的算法属于单通道语音增强。单通道语音增强算法又可以大致分为以下几类：谱减法[2]，基于统计模型的算法[3-4]，子空间算法[5]，以及基于机器学习的算法[6-7]。需要指出的是，这些算法大多只关注幅度谱的修正，而采取使用含噪语音信号相位代替纯净语音信号相位的做法。其原因在于早期研究人员认为人耳对于相位信息并不敏感[8]；在高信噪比情况下，含噪语音信号相位谱和纯净语音信号相位谱非常接近[9]；纯净语音信号相位谱的准确较难估计，会增加算法的复杂度等等。因此，从20世纪开始的很长一段时间范围内，语音增强主要是对信号的幅度谱进行增强。而对于相位谱的研究较少。

随着语音增强技术的发展，仅仅对幅度谱进行增强后实现的效果提升越来越有限。同时硬件资源的提升使得算法复杂度较高的方法也能够被接受。因此，研究人员将目光转向相位谱。Paliwal K等人设计了多种实验证明了相位谱在语音增强中的重要性[10]。近年来，越来越多的研究致力于相位谱语音增强[11-13]。

本文提出了具有相位补偿的改进log-MMSE语音增强算法。本文使用基于GMM的VAD算法[14]来估计噪声和改进基础的log-MMSE增益函数。传统的通过VAD来估计噪声的方法只在噪声段更新，而在语音段保持不变。本文结合VAD所产生的语音存在概率改进噪声功率谱更新方式，使得噪声信息能够一直得到更新。另外根据VAD给出的帧单位上检测结果和语音存在概率改进了基础的log-MMSE增益函数。最后使用一个相位补偿因子[15]来对相位谱作出补偿。从而对含噪语音信号的相位谱和幅度谱同时进行增强。

本文在TIMIT和NOISEX-92，NOIZEUS数据集下，设立多种噪声环境进行算法有效性验证。实验数据表明，本文所提出的具有相位补偿的改进log-MMSE语音增强算法与其他经典语音增强算法相比，能够实现更好的噪声抑制效果，更好地提升语音质量。

2 典型log-MMSE语音增强算法

假设噪声是加性的。则时域中含噪语音信号由可由式(1)来表示。

x(n)=s(n)+v(n)

(1)

其中，x(n)、s(n)、v(n)分别表示时域中的含噪语音，纯净语音和噪声信号。

含噪语音信号经过语音信号预处理过程，从时域变换到频域后，用幅度谱和相位谱表示如下：

|X(k,l)|eiφX(k,l)=|S(k,l)|eiφS(k,l)+

|V(k,l)|eiφV(k,l)

(2)

其中，|X(k,l)|、|S(k,l)|、|V(k,l)|分别表示含噪语音、纯净语音、噪声的幅度谱。φX(k,l)、φS(k,l)、φV(k,l)分别表示含噪语音、纯净语音、噪声的相位谱。

基础log-MMSE增益函数通过令估计纯净语音与实际纯净语音对数幅度谱均方误差最小化推导得出，可以表示如下：

(3)

然后通过增益函数增强幅度谱，并且使用含噪语音相位代替纯净语音相位。最后通过逆傅里叶变换转换到时域上。其过程可以用图1来展示。

3 改进log-MMSE语音增强算法

3.1 改进噪声估计

基于GMM的VAD算法选取子带对数能量作为语音特征，其计算过程如下。

P(k,l)=αP(k,l-1)+(1-α)|X(k,l)|2

(4)

(5)

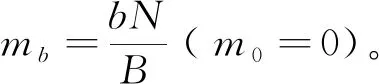
对含噪语音进行建模，GMM可以表示如下(为了表达简洁，式中省略了部分索引)：

(6)

其中，w,μ,κ分别表示权重，均值和方差，这三个值组成GMM参数集λ。下标z=0,1分别表示噪声分量和语音分量标签。

初始化GMM模型参数集之后，对参数集进行实时更新。通过参数集来求得语音存在概率，语音存在概率的计算公式如下：

(7)

其中，spp(b,l)表示第l帧中第b个子带上的语音存在概率，w1(b,l)表示对应的语音模型权重，p(y(b,l)|z=1,λl)表示对应噪声模型的概率密度函数，λl表示第l帧的参数集。子带上的语音存在概率spp(b,l)通过变换可以得到各频点上的语音存在概率spp(k,l)。统计一帧中各子带的语音存在概率，与一个阈值进行比较得到可以每一帧信号的VAD结果。

传统基于VAD进行噪声估计的方法可以表示如下：

(8)

上述方法的缺点是在语音段无法更新噪声功率谱，实际上语音段内的噪声功率谱可能会发生变化。因此本文对上面的噪声估计方法做出了改进，通过一个可变平滑因子使得噪声功率谱更新在语音段也能够进行。改进后的噪声估计方法可以用下式来表示。

(9)

其中αn(k,l)表示第l帧第k个频点上的平滑因子，其计算公式如下：

αn(k,l)=α0+spp(k,l)(1-α0)

(10)

3.2 改进增益函数

前文所给出的基础log-MMSE增益函数是假设语音和噪声都存在时推导得出的。但是人在说话过程中必然会有停顿，此时只有噪声信号的存在。因此对于一段含噪语音信号，一般不直接使用增益函数与之相作用，而需要结合语音存在概率对增益函数作出修正。另外当增强信号幅度为零时，会出现恼人的音乐噪声影响语音质量。因此为了保证增益函数不为零，还需要为其设定一个最小值。

值得注意的是，在有些情况下，GMM的建模可能出错，在这种情况下得到的语音存在概率是有误的，若继续使用其进行语音增强会对语音有较大损伤。尽管频点上的语音存在概率可能会出错，但是帧单位上的VAD判决结果由于子带融合机制一般是正确的，因此本文的增益函数最终设置如下：

(11)

其中G′(k,l)表示本文所用改进增益函数，Gm是为了防止语音存在概率为零时导致最终增益为零所设置的最小增益值，Gn是为了防止原先增益为零时导致最终增益为零所设置的最小增益值。

3.3 相位补偿

在高信噪比情况下，含噪语音的相位与纯净语音相位接近，但在低信噪比情况下，两者的差距会十分明显。因此只对含噪语音进行幅度谱增强而忽略相位谱的做法并不是最优的。我们使用一个简单的实验来说明上述现象。即选取一段纯净的语音信号，叠加高斯白噪声设立多种信噪比。并把这两种信号转换到频域上，观察两者的相位谱，实验结果如表1所示。

表1 不同信噪比情况下含噪语音信号与纯净语音信号相位的比较

信噪比/dB-505101520φX(k,l)/度-28.9-37.3-42.5-45.5-47.2-48.2φS(k,l)/度-49.5-49.5-49.5-49.5-49.5-49.5

可见信噪比越低，两者的差距越来越大。

因此本文使用一个相位补偿因子来对相位谱进行补偿[15]。给出相位补偿因子如下：

Λ(k,l)=cΨ(k)|V(k,l)|

(12)

其中c为一经验值常数，|V(k,l)|表示噪声幅度谱，Ψ(k)为一反对称性函数，其形式如下：

(13)

相位补偿首先通过给原先的含噪信号加上相位补偿因子：

XΛ(k,l)=X(k,l)+Λ(k,l)

(14)

然后通过上式中的XΛ(k,l)来求得补偿后的相位谱：

φXΛ(k,l)=ARG[XΛ(k,l)]

(15)

最终的增强信号通过结合增强之后的幅度谱和补偿的相位谱来得到：

(16)

3.4 本文改进算法总结

综上所述，本文所提出的改进语音增强算法主要研究内容如下：

(1)使用基于GMM的VAD算法所得到的语音存在概率，改进了传统通过VAD算法进行噪声估计的方法，使得噪声功率谱更新在语音段也能够进行。

(2)使用基于GMM的VAD算法所得到帧单位上检测结果和语音存在概率，改进了基础的log-MMSE增益函数，在尽可能抑制噪声的同时尽量保证语音成分不失真。

(3)使用相位补偿因子对相位谱作出补偿，从而同时进行幅度谱和相位谱的增强。

本文所设计的具有相位补偿的改进log-MMSE语音增强算法的整体流程图如图2所示。

4 实验验证

为了评估所提出的具有相位补偿的改进log-MMSE语音增强算法的性能，我们从TIMIT语料库中选择纯净语音信号。并从NOISEX-92和NOIZEUS噪声库中选取噪声，对纯净语音信号叠加不同的噪声，设立多组信噪比作为测试数据，对比本文算法与其他经典语音增强算法的性能。

本文使用信噪比和PESQ来评价增强之后的语音质量。算法处理后的信号信噪比越高意味着噪声抑制的效果越好。但语音增强不仅仅是对噪声进行抑制，还需要同时尽量保证语音成分不失真。语音质量感知评价(PESQ)是一种比较常用的客观评价方式。PESQ给出的得分越高，则说明增强的语音质量越高。通过这两种评价方式来对比算法的性能。本文中语音信号采样频率为16 kHz，帧长20 ms，平滑功率谱平滑常数α取0.98，噪声功率谱平滑常数α0取0.75，增益控制值Gm取0.103，增益控制值Gn取0.001，相位补偿因子常数c取3.74。

4.1 不同噪声环境下各算法输出信噪比对比

首先从NOISEX-92噪声库中选取平稳噪声：white噪声和pink噪声，以及非平稳噪声babble噪声构成不同的含噪信号，通过信噪比来对比本文算法和其他经典算法的降噪性能。表2展示了不同噪声环境下，使用其他算法和本文算法进行增强后的输出信噪比情况。

表2 多种噪声环境下各算法的输出信噪比比较

噪声类型输入信噪比/dB输出信噪比/dB谱减法维纳滤波Log-MMSE本文算法-50.411.532.067.03white04.734.334.939.4359.057.668.2011.851013.4211.2711.8114.20-51.02-0.021.616.41pink04.574.574.908.8958.698.698.0911.511013.3911.6512.1414.21-50.381.962.162.91babble04.205.375.676.2558.248.889.179.731012.7513.2713.5313.39

从表3的实验结果我们可以看到，除了在babble噪声含噪语音信号输入信噪比为10 dB情况下，本文算法的输出信噪比略低于log-MMSE，其余情况下本文算法的输出信噪比都高于其他算法。

为了直观形象地展示其他语音增强算法和本章所设计的算法的效果。图3展示了在white噪声0 dB情况下各算法输出波形图。从图3我们可以看到相对而言谱减法的噪声抑制效果最差，谱减法在高信噪比情况下能够取得不错的噪声抑制效果，但是在低信噪比情况下，其效果会急剧下降。在低信噪比情况下，维纳滤波具有较小的增益函数，因此具有更强的噪声抑制效果。但与此同时，和纯净语音信号的波形图对比可以看到，一些有效语音成分也被消除掉，这是我们不希望看到的结果。log-MMSE保留了更多的语音成分，但也残留了较多噪声。而本文算法最终的增强效果既最大程度保留了语音的有效成分，也具有更低的噪声残留。

4.2 不同噪声环境下各算法PESQ对比

为了进一步验证本文算法的有效性。除了在NOISEX-92中选取的噪声，另外从NOIZEUS噪声库中选取日常生活中常见的street噪声和car噪声组成测试集。对比各算法处理后的PESQ值，结果如表3所示。

表3 多种噪声环境下各算法的PESQ比较

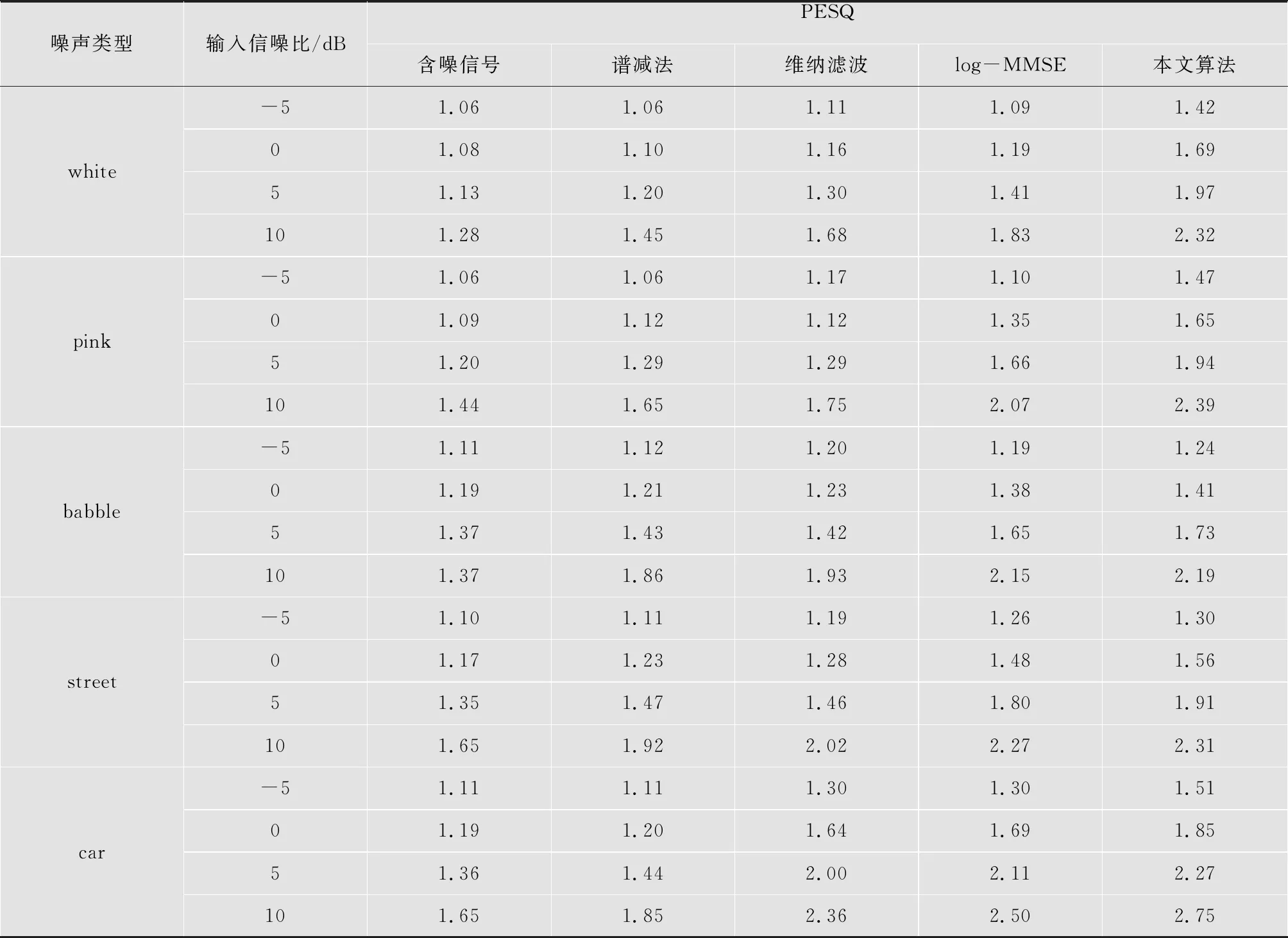
噪声类型输入信噪比/dBPESQ含噪信号谱减法维纳滤波log-MMSE本文算法white-51.061.061.111.091.4201.081.101.161.191.6951.131.201.301.411.97101.281.451.681.832.32pink-51.061.061.171.101.4701.091.121.121.351.6551.201.291.291.661.94101.441.651.752.072.39babble-51.111.121.201.191.2401.191.211.231.381.4151.371.431.421.651.73101.371.861.932.152.19street-51.101.111.191.261.3001.171.231.281.481.5651.351.471.461.801.91101.651.922.022.272.31car-51.111.111.301.301.5101.191.201.641.691.8551.361.442.002.112.27101.651.852.362.502.75

从表3中结果可以看到，本文算法在各种噪声环境下都具有最高的PESQ得分。因此本文算法比其他算法更好的增强效果。

5 结语

本文提出了具有相位补偿的改进log-MMSE语音增强算法。传统的通过VAD来估计噪声的方法只在噪声段更新，而在语音段保持不变。本文结合基于GMM的VAD所产生的语音存在概率改进噪声功率谱更新方式，使得噪声信息在语音段也能更新。另外结合VAD给出的帧单位上检测结果和语音存在概率改进了基础的log-MMSE增益函数。最后使用一个相位补偿因子来对相位谱作出补偿。从而对含噪语音信号的相位谱和幅度谱同时进行增强。在多种噪声环境下的实验结果表明，本文提出的算法相比于其他经典语音增强算法，具有更好的噪声抑制效果，能够获得更好的语音质量。