基于归一化随机共振的水下微弱目标检测方法

王 雪

(杭州应用声学研究所，浙江 杭州 310023)

随着舰艇声隐身技术的快速发展[1]，可接收到的线谱信号能量变小，信噪比降低，使得更难被声纳系统探测得到。在低信噪比下，声信号已经淹没在环境噪声背景中，传统线性滤波的方法通过抑制噪声能量来提高信噪比，但是在滤去噪声的同时信号有所损失[2]，检测方法能力有限，很难将信号从噪声背景里提取出来。与传统线性滤波方法相比，一种非线性理论--随机共振(Stochastic Resonance, SR)系统在一定条件下噪声不但不会削弱信号检测效果，还可以实现噪声能量大幅度向信号转移，使得输出信噪比提高。但是经典随机共振理论要求信号为小参数信号(频率远小于1 Hz)，然而实际工程中需要探测上百、上千赫兹的水下线谱信号。为此，本文应用了一种归一化随机共振方法，通过选取合理的随机共振系统参数，实现大参数微弱信号的检测。

1 经典双稳态系统随机共振系统

在噪声对非线性系统的作用中，双稳态系统是研究最多的一类非线性系统，受到噪声n(t)与外部周期驱动力s(t)=Acos(2πft)作用的双稳态系统可以由下面的Langevin方程(LE)描述，即

dx/dt=ax-bx3+Acos(2πft)+n(t)

(1)

式中x(t)为双稳态系统输出信号，a、b为系统的结构参数，n(t)为均值为零，强度为D的高斯白噪声，且有E[n(t)n(t+τ)]=2D0δ(τ)。噪声n(t)也可表示为：

(2)

式中，σ2为噪声功率，ξ(t)为零均值、方差为1的高斯白噪声。式(1)描述了系统粒子在随机力n(t)与外部周期驱动力s(t)共同作用下的运动，将会产生随机共振现象，噪声能量会向周期信号能量转移，使周期信号放大，且输出频谱图在周期信号频率f处出现峰值。由于双稳态系统的绝热近似理论及线性响应理论的限制[3-5]，经典双稳态系统只能应用于小参数信号即信号频率远小于1 Hz、幅值远小于1 V的处理，这就导致了其在工程领域中的应用范围很小。而归一化随机共振方法可以克服这一限制。

2 归一化随机共振系统

(3)

进一步简化为：

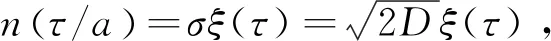
(5)

(6)

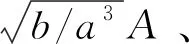
3 归一化随机共振系统参数的选取及仿真实验

首先，确定一组合理的归一化系统参数，即在式(1)中，当a=b=1时可产生随机共振现象的周期信号频率f及噪声强度D的值。参考文献[6]中，本文选定归一化后的输入参数为：f0=0.01 Hz，D0=0.31。

对于接收到的频率为f、噪声强度D的带躁线谱信号则有：

(7)

(8)

根据式(7)及式(8)，可以计算出归一化前的双稳态系统参数a、b。再解式(1)就得到了随机共振系统的输出。

本文中均使用四阶龙格库塔算法对LE进行数值仿真，系统初值都设为0。对于一个小参数信号，设线谱信号频率f=0.01 Hz，幅度A=0.1，噪声强度D=0.31。采样频率fs=5 Hz，采样点数为2 000。图1给出了小参数信号的经典双稳态随机共振系统(系统参数为1)的输入与输出的对比图。从图1(a)、(b)中可知，线谱信号已经完全淹没在噪声背景中，此时的功率信噪比为-20 dB；图1(c)、(d)说明经过了随机共振系统的处理，噪声能量明显降低、线谱信号能量得到大大加强，且频谱图在信号频点f=0.01 Hz处明显看到一条谱线且为峰值，即随机共振理论可用于微弱小信号的检测。

当输入信号为大参数信号时，经典随机共振方法则不再适用。图2中，取输入信号的线谱频率f=100 Hz，采样率为50 kHz即保持采样频率与信号频率的比值不变，仍然取2 000个采样点；其余参数与图1中的保持不变。从图2的输入、输出频谱对比中发现，在图2(b)中，在线谱频点f=100 Hz处频谱能量非常小，经典随机共振方法并不能提高微弱的大参数信号的信噪比。

在图3中，采用与图2的仿真实验一样的输入参数和采样参数，不同的是使用了归一化随机共振方法对双稳态系统参数a、b进行了选取。根据式(7)及式(8)，计算可得：a=f/f0=100/0.01=1 000；b=a3(D0/D)=1×1012。对比图3(d)与图2(b)，在图3(d)的线谱频点f=100 Hz处出现明显谱峰，在噪声背景中凸现出来，轻松实现了线谱的检测。说明经过归一化的处理，随机共振理论也可以应用于大参数微弱信号的检测中。

同样地，归一化随机共振对于噪声幅度大于1的大参数信号检测仍然有效。如图4中的仿真实验，不仅线谱频率f=100 Hz远大于1，噪声强度D=12.5也大于1，线谱信号幅度设为A=0.7。同样根据式(7)及式(8)，计算可得：a=f/f0=100/0.01=1 000；b=a3(D0/D)2.48×1010。采样参数与图3中相同。在输出中也可以发现归一化随机共振在大参数微弱信号检测中可以发挥强大的作用。

4 结语

本文从实际工程应用中水下微弱目标信号常常不能满足经典随机共振的小参数条件限制入手，引入了双稳态系统的归一化变换，利用归一化随机共振的方法实现了大参数信号的随机共振。在此基础上，给出了归一化随机共振的系统参数选取方法，并通过几个仿真实验验证了该方法的有效性。