经验小波变换在回转窑故障检测中的应用研究
胡航宇,张 云
(1.武汉理工大学 机电工程学院,湖北 武汉 430070;2武汉理工大学 建材行业回转窑检测技术中心,湖北 武汉 430070)
水泥回转窑是建材行业的主要生产设备,其运行工况复杂,具有长期运转和高温重载等特点。为了保证水泥厂的经济效益,回转窑需要处于长期健康稳定的运行工况。托轮的运行状况决定了回转窑是否能长时间正常运行[1]。在已知的回转窑故障类型中,筒体中心线的偏移和筒体热弯曲变形均可引起托轮振动[2]。张云等[3-4]通过建立托轮动力学模型,并进行数值仿真分析,确定了故障特征频率与故障源之间的关系,为研究托轮振动信号的处理方法提供了理论基础。
托轮振动信号是由多种故障源共同作用引起的非线性、非平稳信号,如何有效提取信号中的特征频率成为关键问题。Huang等[5]提出了经验模态分解(empirical mode decomposition, EMD),它是一种自适应的信号时频分析方法。该方法平稳化处理信号,逐层地分解信号中存在的不同尺度的波动,生成一组特征模态函数(intrinsic mode function, IMF),其具有不同特征尺度。相较于传统方法,EMD消除了许多无物理意义的简谐波,使信号分析更灵活方便。张云等运用EMD方法处理托轮振动信号[4]和筒体外轮廓信号[6],分析筒体的故障类型。然而,EMD方法没有严密的理论基础,且受自身算法以及原始信号频率特性的影响,分解的结果可能会出现模态混叠现象。针对EMD方法存在的不足,Gilles[7]结合小波分析理论和EMD的自适应性优势,提出经验小波变换(empirical wavelet transform,EWT)方法。EWT方法根据信号的傅里叶频谱自适应地划分,然后构建合适的正交小波滤波器组,将信号分解为多个含有不同频率特征信息的调幅调频(amplitude modulation-frequency modulation,AM-FM)成分[8],从而实现信号的特征提取。EWT方法的理论基础完备,且计算量远小于EMD方法,已在多个领域得到应用。
笔者提出一种基于EWT的回转窑托轮振动信号特征提取方法,并与EMD方法相比,仿真结果验证了EWT方法的有效性。将EWT成功应用到托轮振动信号的故障数据分析中,与其他回转窑故障检测方法结果进行对比,验证了该方法的正确性。
1 经验小波变换
EMD方法将信号f(t)分解成N个本征模态函数(intrinsic mode function,IMF)ck和残差rn的总和:
(1)
由于不合理的收敛条件以及包络过度和包络不足等问题,该方法容易引起模态混叠,并且筛分迭代过程也缺乏理论基础。为了解决这个问题,Gilles采用经验小波变换方法,将信号f(t)分解为N+1个固有模态函数fk(t)的总和:
(2)
式中:fk(t)被定义为调幅-调频(AM-FM)函数:
fk(t)=Fk(t)cos(φk(t))
(3)
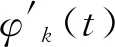
经验小波变换方法以小波分析为理论基础,根据信号自身的傅里叶谱特性对其进行划分,自适应地选择一组小波滤波器以提取信号的不同AM-FM分量。在分析过程中把傅里叶频谱定义在[0,π]范围内,把它分割成N个部分,ωn为各部分之间的边界,其中ω0=0,ωN=π,则每个频带可表示为:
Λn=[ωn-1,ωn],n=1,2,…,N
(4)
以ωn为中心,Tn=2τn被定义为过渡段,如图1中的阴影区域所示。
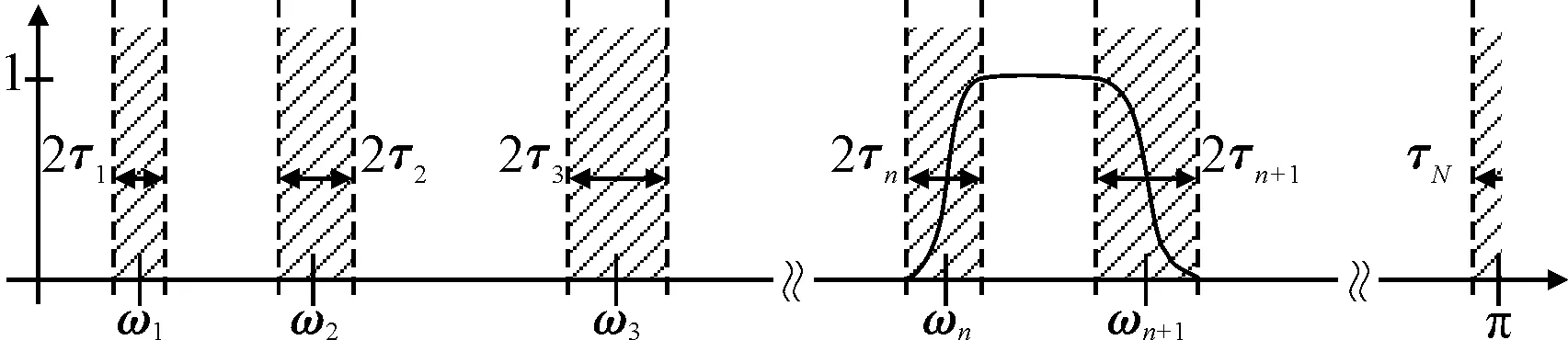
图1 傅里叶轴的分割
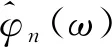
(5)
(6)
式中:
β(x)=x4(35-84x+70x2-20x3)
(7)
τn=γωn0<γ<1
(8)
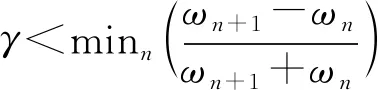
Wfe(n,t)=[f(t),ψn(t)]=
(9)
Wfe(0,t)=[f(t),φ1(t)]=
(10)
结合以上公式,原始信号重构公式如下:
(11)
调幅-调频信号fk(t)定义如下:
(12)
(13)
2 仿真研究
假设筒体转速为3 r/min(0.05 Hz),托轮转速为12 r/min(0.2 Hz),分别用正弦信号S1和S2表示,如式(14)。考虑到回转窑的实际运行工况,添加了间歇震荡高斯脉冲信号S3,则仿真信号S由S1、S2和S3组成,仿真信号的时域波形图及其组成成分如图2所示。这里,采样频率为100 Hz,采样点为10 000。
S1=0.4sin(2π·0.05·t+π/2)
S2=0.6sin(2π·0.2·t+π/3)
(14)
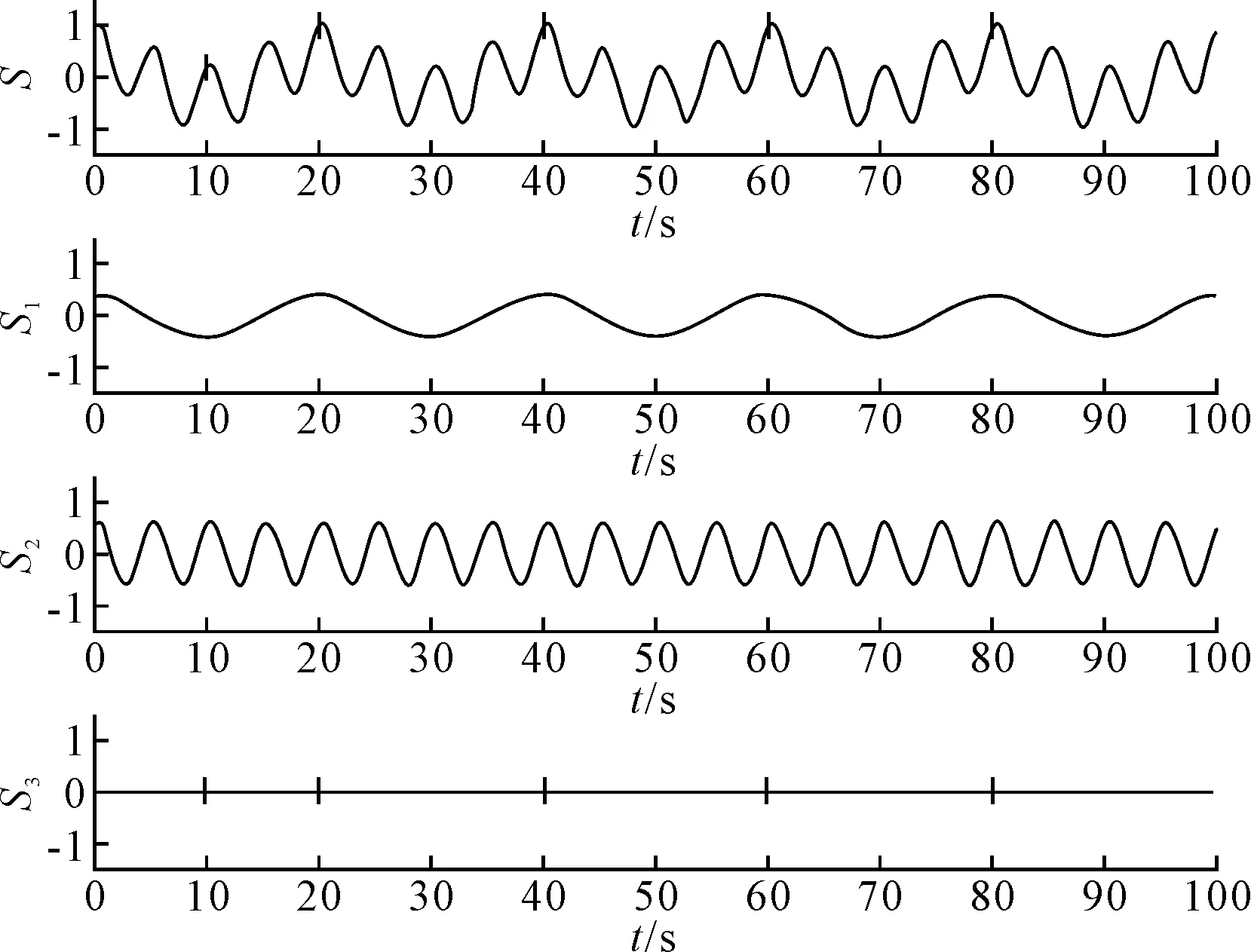
图2 仿真信号S的时域波形及其组成成分
一个尺度函数和多个小波函数分别滤波可获得EWT的输出结果,由于已知信号S的频率成分,故取N=3。图3显示仿真信号的傅里叶频谱及已检测到的频谱边界。仿真信号的EWT分解结果如图4所示,EWT分解出了4个模态分量,后3个模态分量的时域特征与仿真信号的原始分量具有高度一致性。
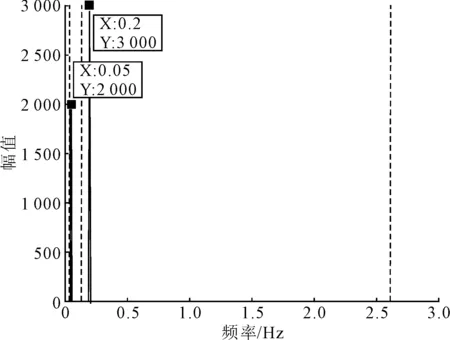
图3 仿真信号的频谱及支撑边界
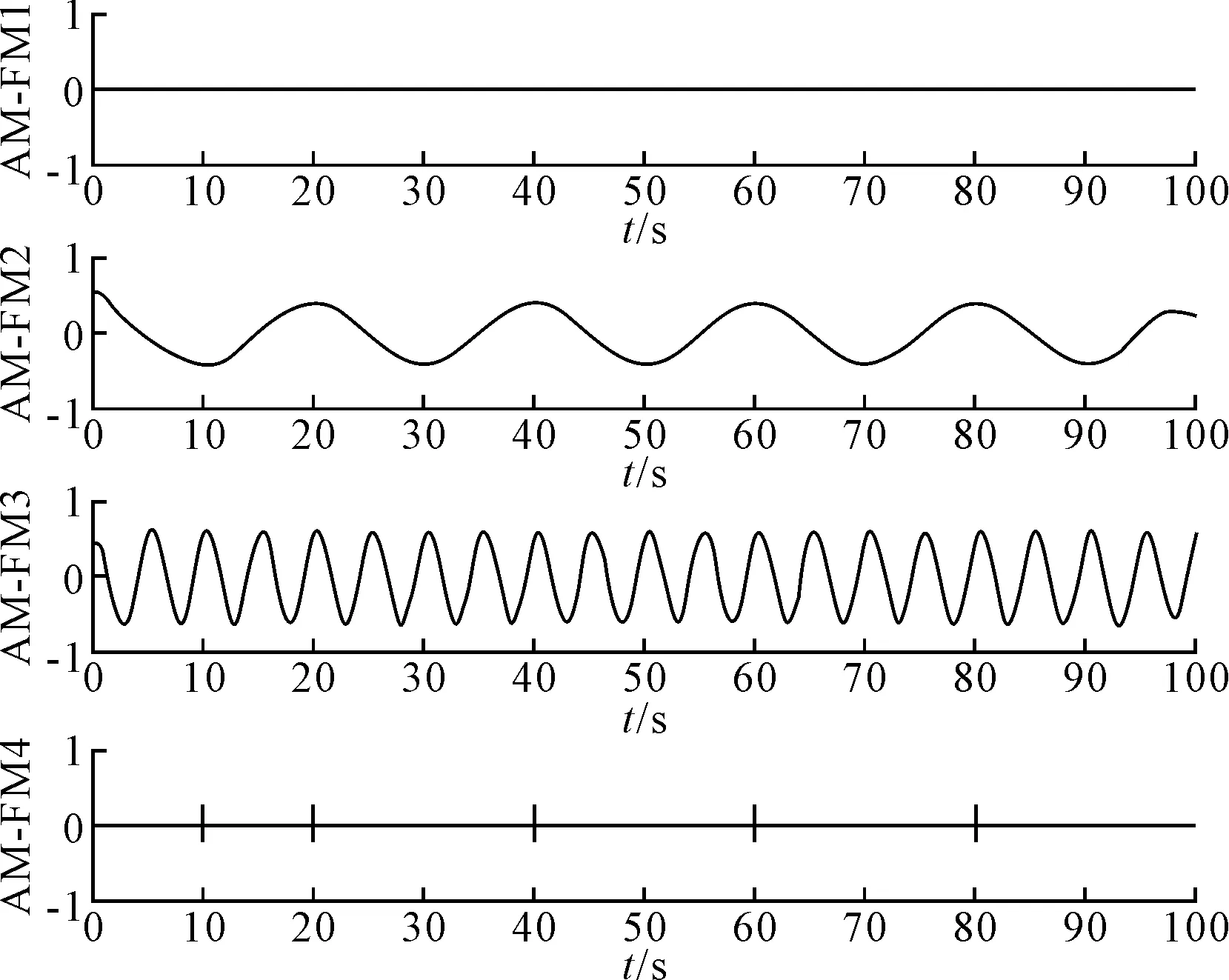
图4 仿真信号的EWT分解结果
为了与EMD方法对比分析,仿真信号S的EMD结果如图5所示。从图5可知,EMD并没有分解出仿真信号的固有模态,而且出现许多虚假的模态分量,谱线混叠较为严重,而EWT分解出仿真信号固有的3个模态函数。理论上,EMD分解得到的本征模态函数IMF并不能保证严格的正交性,如果没有严格的理论支持,很容易发生模态混叠现象,这会影响瞬时频率的表达。EMD产生模态混叠的主要原因是信号的不连续性,时间尺度出现跳跃性变化。当EMD方法选用的终止条件不合理或构造包络线算法的自适应性较差时,也会产生模态混叠现象。另外,每个IMF被分解出来都要经历多次迭代,并且计算量较大。相比之下,经验小波变换是基于小波理论建立的方法,理论基础完备,其计算量要远小于EMD方法。因此,在处理此类信号方面,EWT分解效果优于EMD方法。
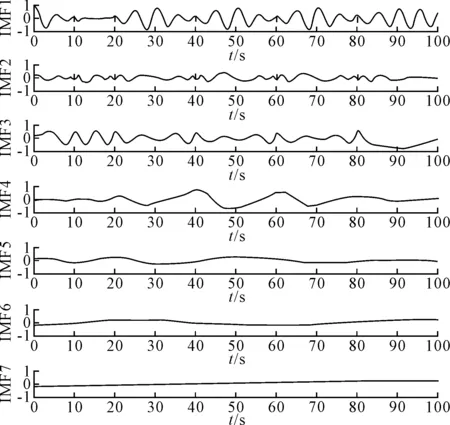
图5 仿真信号的EMD分解结果
3 实验研究
为了检验经验小波变换的有效性,将经验小波变换运用到运转中回转窑托轮振动信号数据处理中。图6为托轮振动数据采集装置,包括一个电涡流传感器,一个霍尔开关,NI数据采集卡以及笔记本电脑。

图6 托轮振动数据采集装置
在测量现场中,筒体转速约为4 r/min,采样频率为100 Hz,采样点数为8 000,利用电涡流传感器获得6个托轮的振动信号。以二挡右托轮为例,图7为测量数据的时域波形图,对其进行经验小波变换。由于EWT频谱分割是自适应地从低频向高频进行划分,且已知低速旋转的托轮和筒体的工频,只需将两个低频特征成分提取出来即可,取N=4,其傅里叶频谱及已检测到的支撑边界如图8所示,图9为经验小波变换的结果。图10为EMD的分解结果。
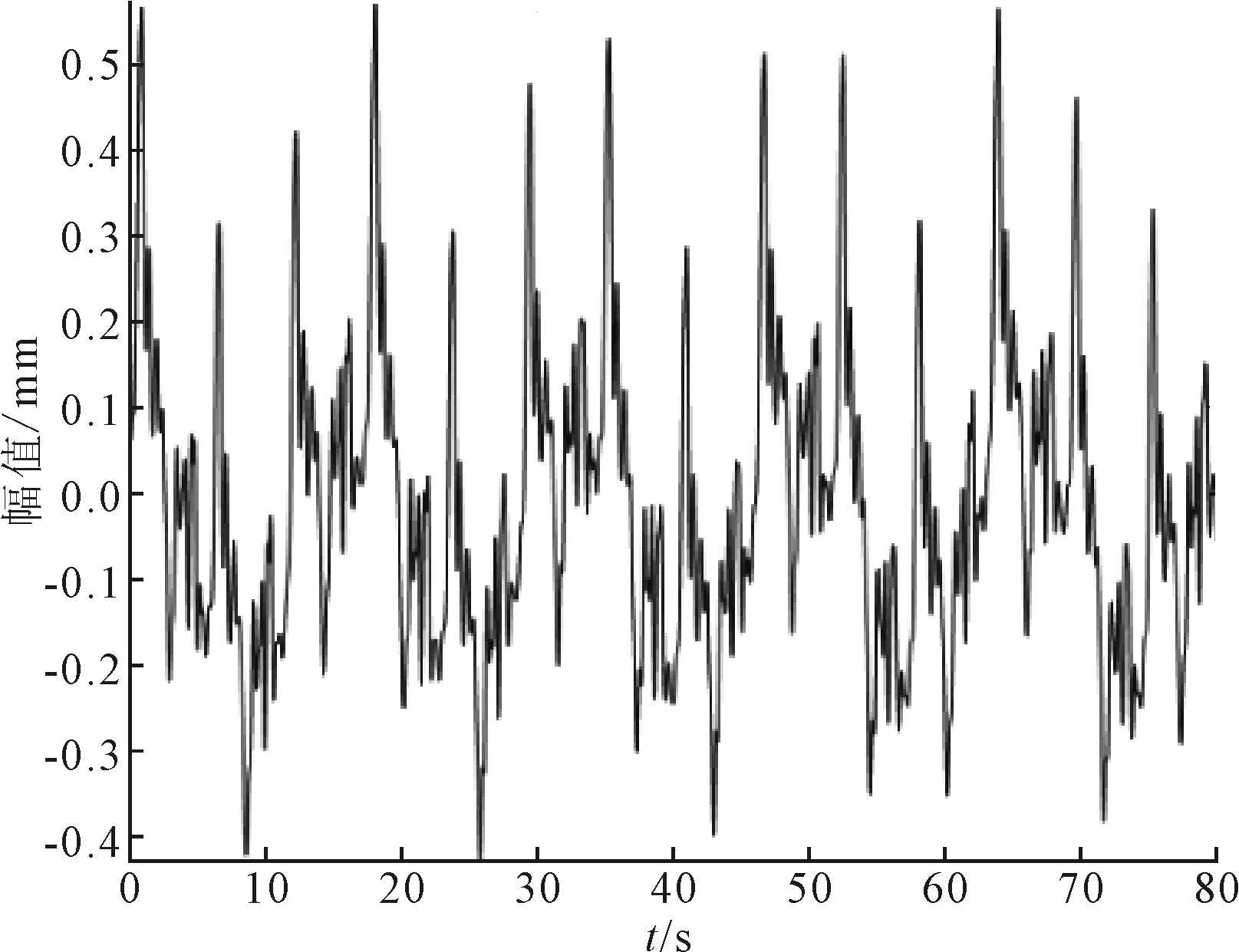
图7 托轮振动信号时域图
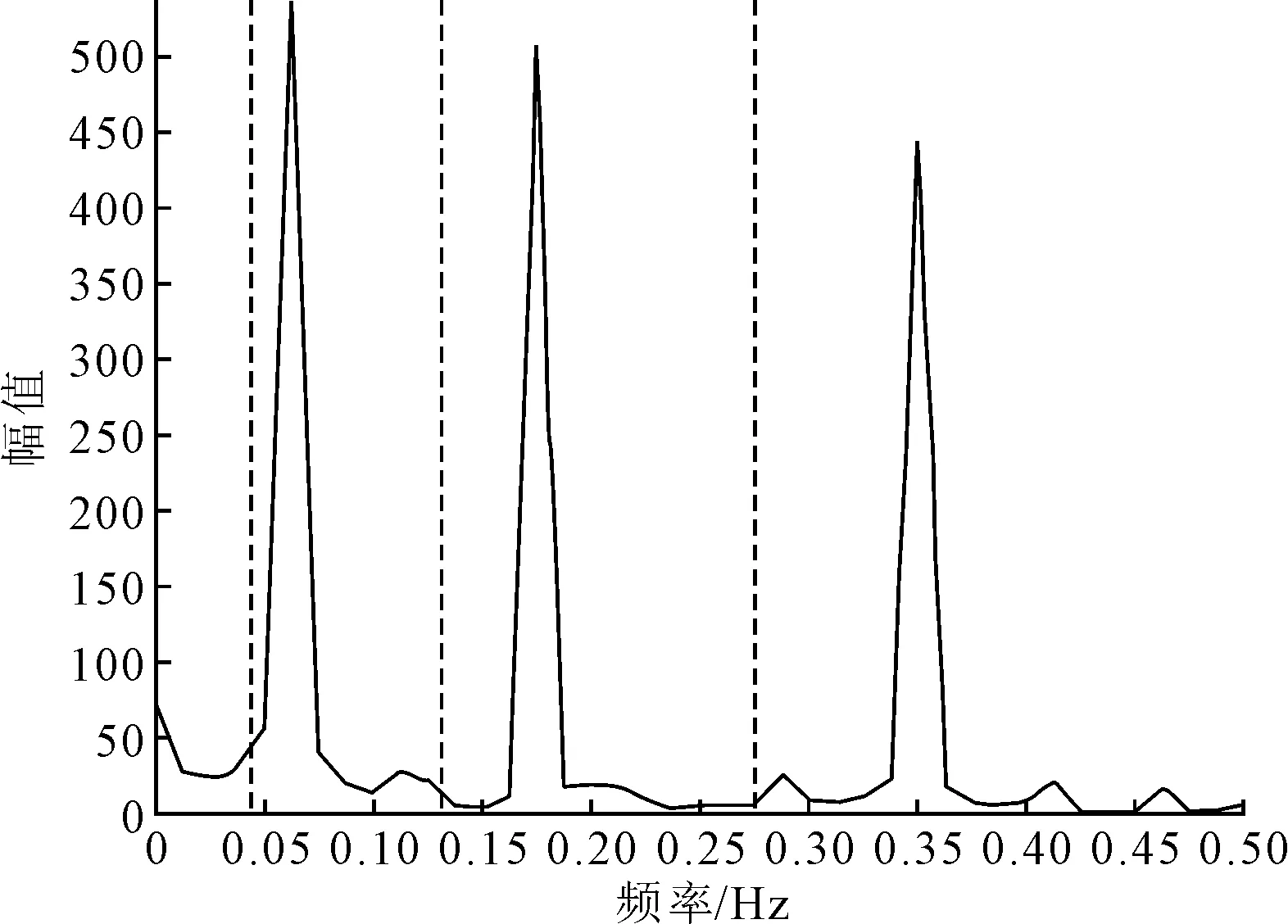
图8 托轮振动信号的频谱图及支撑边界
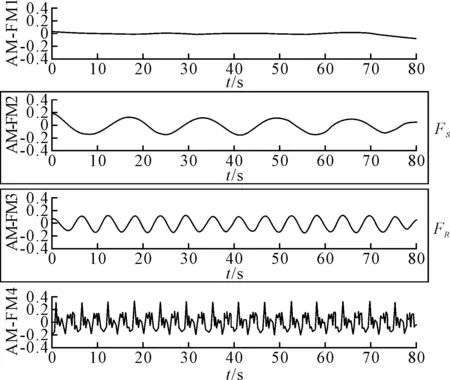
图9 托轮振动信号的经验小波变换
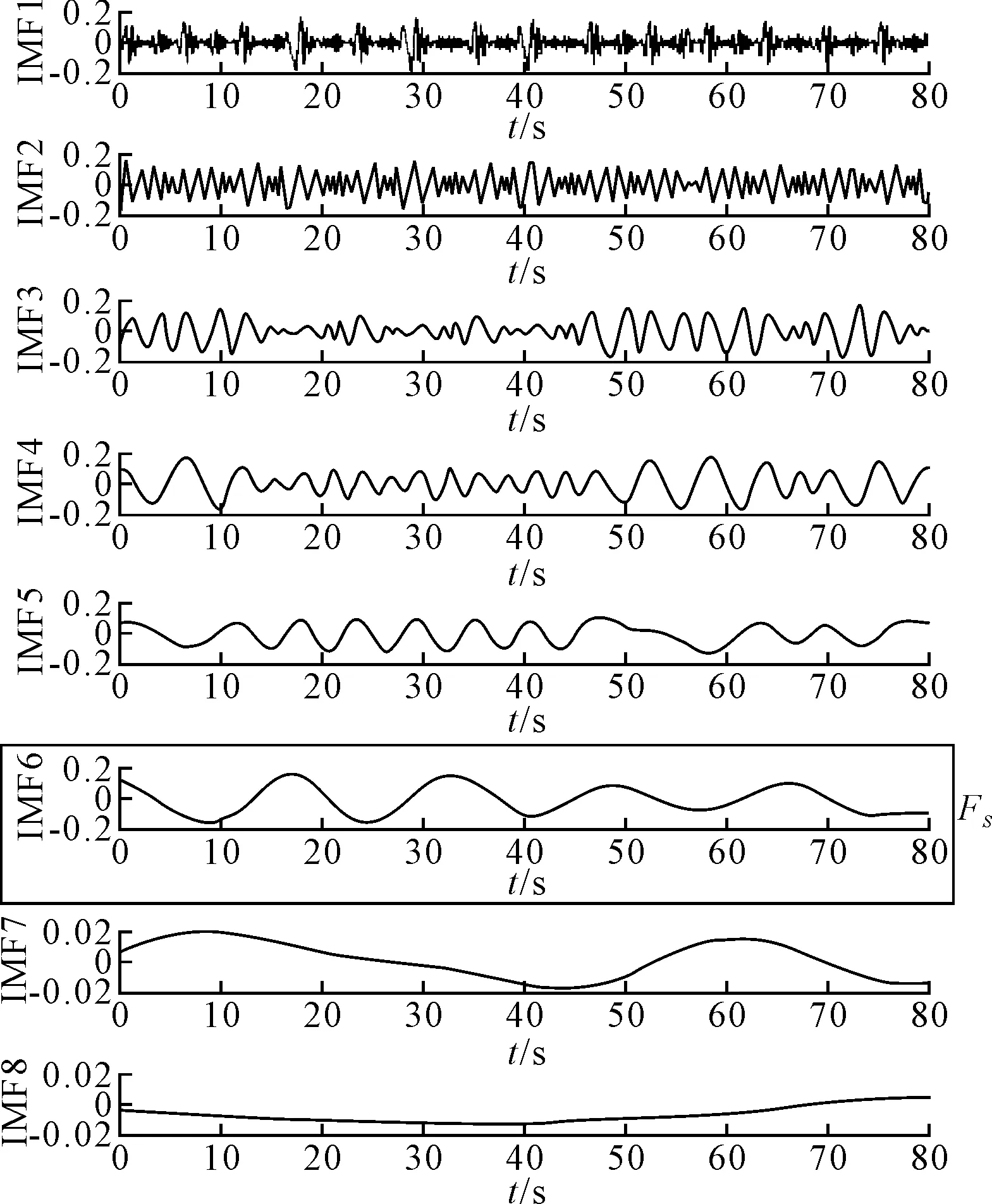
图10 托轮振动信号的经验模态分解
由图8可知,与筒体、托轮工频一致的两个谐波频率被分割出来。从图9可知,EWT分解信号得到4个AM-FM分量,其中第2个AM-FM分量反映了筒体特征频率,第3个AM-FM分量体现了托轮特征频率FR,谱线刻画清晰光滑。而从图10可知,EMD方法得到的IMF6与筒体特征谐波FS比较一致,但其余IMF均不能体现出托轮特征频率FR,模态混叠现象严重,主要原因是多个时间尺度特征成分被分解到一个IMF中,故不能进行下一步信号分析处理。
由上述分析可知,根据信号的频率特征,EWT方法可以自适应地由低频往高频方向分解回转窑托轮振动信号。相比于EMD方法,EWT方法提取的特征模态分量更能体现托轮振动信号的固有特征,刻画的谱线更清晰准确,有利于依照托轮振动信号特征进行下一步的回转窑故障诊断分析。
4 EWT方法适用性验证
运用EWT方法处理6个托轮挠度信号,所得特征AM-FM信号中谐波FR和FS所对应的幅值统计分别如图11所示。由图11(a)可知,2档FR幅值最大,3档FR幅值最小,可以判断筒体2档处筒体弯曲变形最大,3档处筒体弯曲变形最小。由图11(b)可知,幅值大小代表左右托轮受力的相对大小,则1档左托轮径向受力明显小于右托轮,筒体中心偏右;2档左托轮径向受力略大于右托轮,筒体中心略偏左;3档左左托轮径向受力大于右托轮,筒体中心偏左。
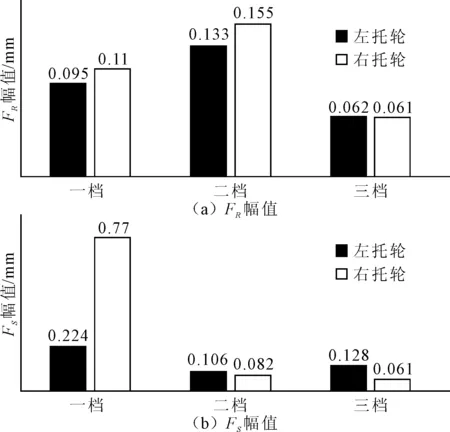
图11 各档谐波幅值对比图
为了验证EWT方法在回转窑托轮振动信号分析中的正确性,采用激光测距法[9]和筒体椭圆度测量法[10]分别对筒体弯曲变形和中心线偏移进行分析。激光测距法通过将激光测距仪对准筒体的截面中心,测得筒体旋转一周的距离,将其通过最小二乘圆法拟合得到筒体的偏心值,结果如表1所示。二档偏心值最大,为1.83 mm;三档偏心值最小,为0.83 mm。结果说明二档筒体截面变形最大,三档筒体截面变形最小,这与图11(a)结果一致。

表1 各档筒体截面偏心值 /mm
筒体椭圆度测量法使用筒体椭圆度电子测量仪,将其吸附在轮带附近的筒体表面某点上旋转,由位移传感器测得筒体表面的该点旋转一周的位移变化量,测量原理如图12所示。3个档位的筒体椭圆度测量结果如图13所示,对比各档位R和L的大小,一档右托轮受力大于左托轮,说明一档处筒体中心偏向右托轮,二档和三档右托轮受力均小于左托轮,说明二档和三档筒体中心偏向左托轮,与图11(b)结果一致。
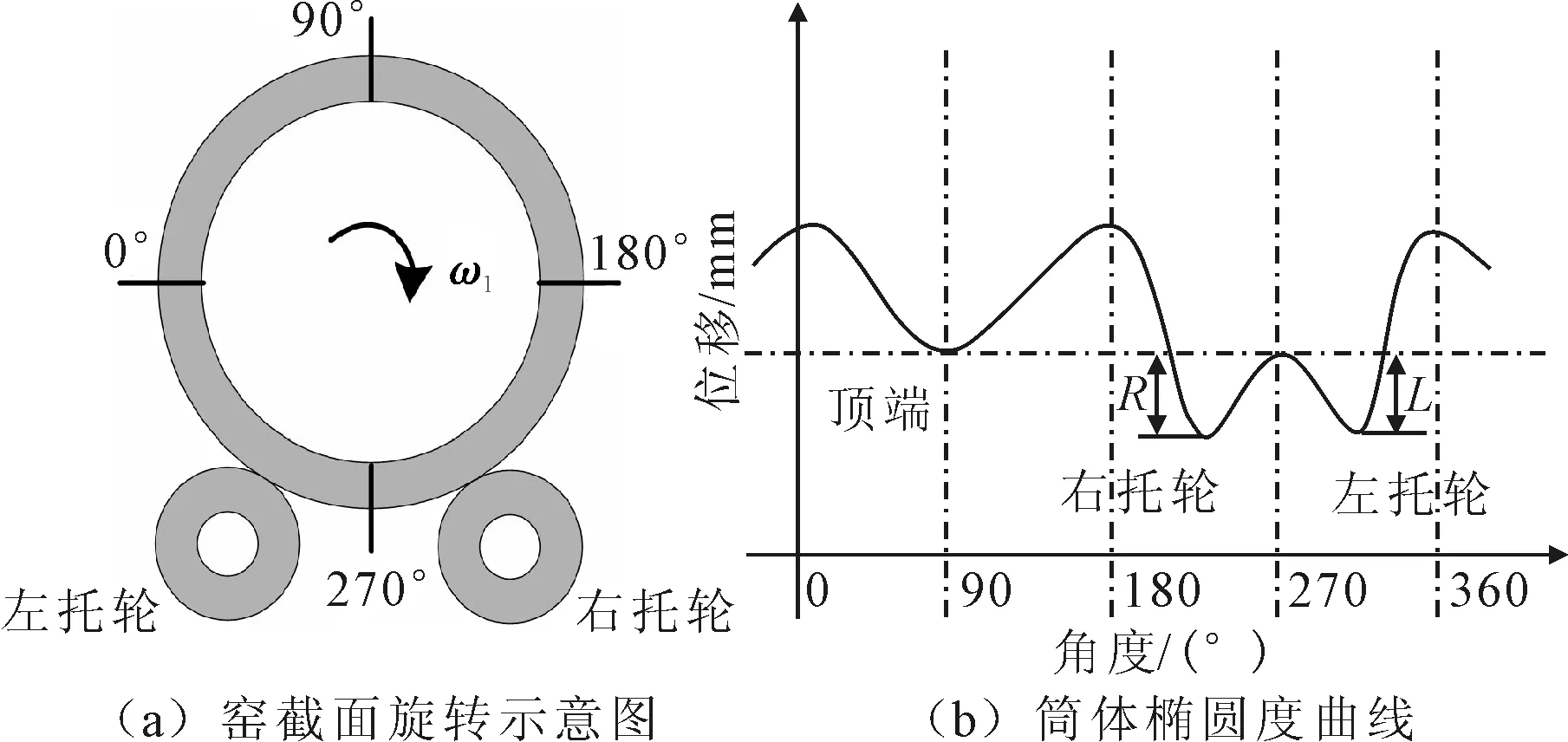
图12 筒体椭圆度测量原理
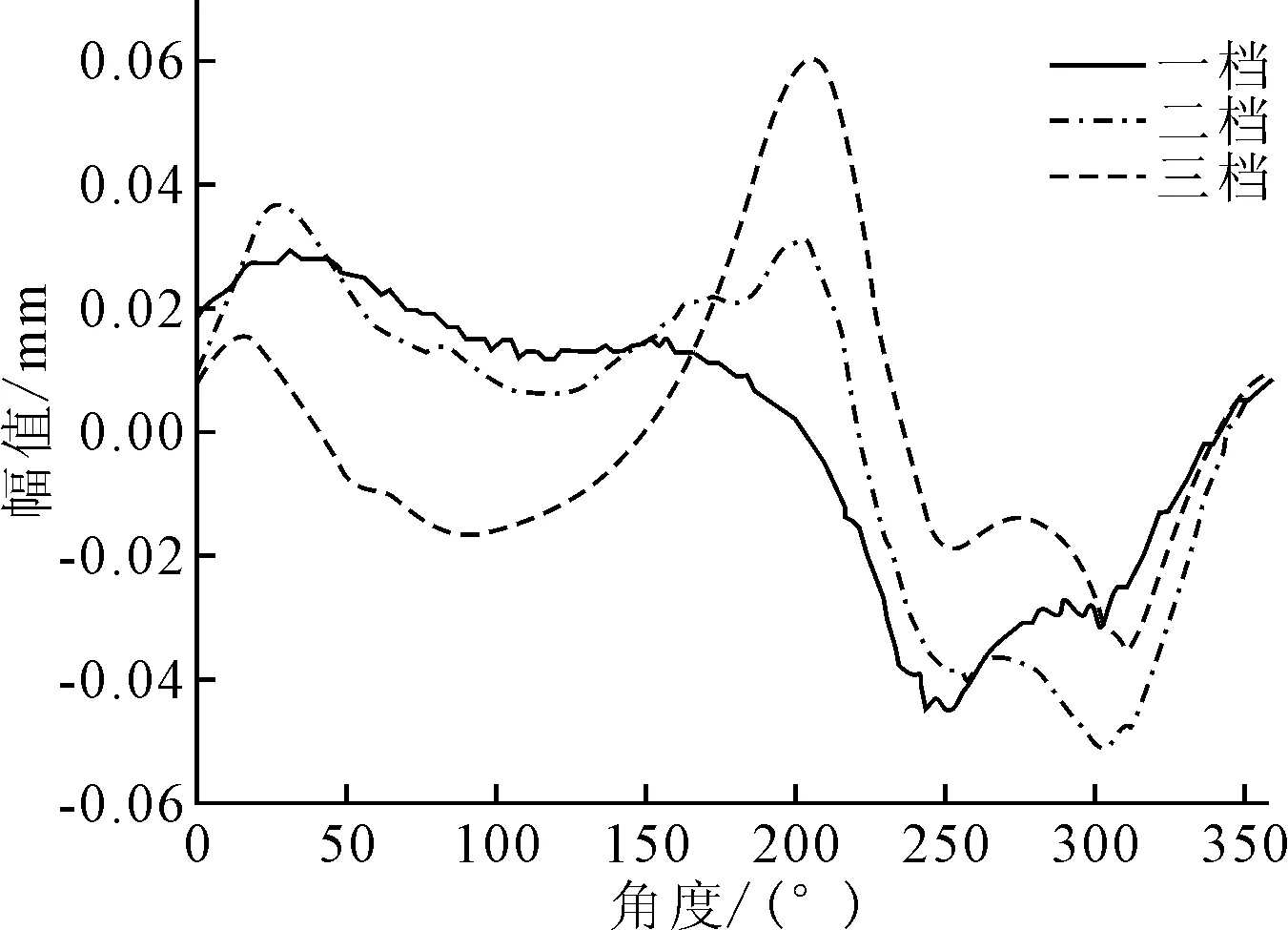
图13 椭圆度测量结果
由以上分析可知,通过将EWT方法分解结果与激光测距法和筒体椭圆度测量法结果对比,验证了EWT方法在回转窑故障检测中的正确性。
5 结论
笔者介绍了EWT方法,根据实际信号特征进行了仿真研究,并将EWT运用于回转窑托轮振动信号分析中。仿真研究和实验结果表明,EWT分解效果明显优于EMD方法。最后将EWT处理结果与传统回转窑检测方法测量结果进行对比,验证了EWT方法在回转窑托轮振动信号分析中的正确性,为后期进行回转窑故障诊断研究打下了良好基础。

