太阳跟踪误差模型多参数全局敏感性分析

龚 俭，李 鹏，罗 琦，雷 旺

(武汉理工大学 机电工程学院，湖北 武汉 430070)

太阳跟踪技术通常是指使太阳跟踪器根据太阳的运动轨迹作相应机械运动，并使太阳光线能够随时垂直入射太阳能光伏组件的表面[1-2]。在实际应用中，由于机械加工、组装以及现场安装等因素的复杂性，导致存在多种误差源影响太阳跟踪系统精度，从而影响系统发电效率，研究各因素对跟踪精度的影响及影响程度对提高跟踪系统精度十分重要[3]。文献[4]分析了不同误差源对太阳跟踪系统精度的影响，并给出误差源单独作用时的影响。由于系统正常运行时，并不是受到各个误差源的单独影响，通常是受到多种误差源同时作用且相互之间存在较强的耦合效应，因此，当系统受多误差源同时作用时，各个误差源对系统总的影响相比各误差源单独作用时的影响会有所差别，而当误差源较多且系统较为复杂时，这个差别会更显著[5]。为此，笔者利用全局敏感性分析方法研究主要误差源及其间相互作用对跟踪精度的影响关系，以达到各误差源对系统精度的敏感性认知。

采用敏感性分析来评估模型输入的变化如何影响其输出，从而确定模型输入参数或一组模型输入参数的变化影响模型输出的程度[6]。模型参数敏感性分析可以识别模型关键参数、诊断模型结构，是模型创建和应用的关键步骤之一[7]。敏感性分析又分为两类：局部敏感性分析和全局敏感性分析。局部敏感性分析通过一次改变一个输入参数同时保持其他参数为定值来检查输出的局部响应，虽然操作容易，但由于依赖其他参数值而导致“异参同效”现象的存在，其局限性较大[8-9]。全局敏感性分析则是所有参数在整个参数空间上同时变化，允许同时评估多个参数对模型输出的影响以及各参数的相互作用，较适用于复杂系统的分析[10]。常用的全局敏感性分析方法有回归分析法、FAST法、RSA法和Sobol法等方法，其中，基于方差原理的Sobol法具有计算简便、计算结果准确可靠等优点，是最常用的全局敏感性分析方法之一[11-13]。

笔者以太阳双轴跟踪器为例，利用Sobol方法，以太阳跟踪误差作为敏感性分析模型的目标函数，分别对夏至、秋分以及冬至时的跟踪误差模型各参数的单独作用以及参数的全局敏感性进行了深入分析。研究结果有助于理解跟踪模型参数的敏感性, 可为模型的参数校正和应用提供指导。

1 太阳跟踪误差数值模型

由文献[14]可知，制造安装过程引起的主要误差源包括：方位轴倾斜φ、俯仰轴和方位轴不正交γ、基座相对立柱旋转ε和编码器零点偏移。图1(a)为太阳跟踪误差空间示意图，太阳光线采用平行光束模型,根据太阳跟踪器光伏组件指向和太阳入射光线的偏差简化得到。图1(b)分别是俯仰轴和方位轴不正交γ、方位轴倾斜φ和基座相对立柱旋转ε的平面示意图。以跟踪器俯仰轴和方位轴正交点为原点O，正东为X，正南为Y，正上方(天顶)为Z建立坐标系，OA为太阳入射光线矢量S在水平面上的投影，通常约定OA与正南方向夹角ω为太阳方位角，并规定顺时针为正，因此ω∈(-180°，180°)；OA与矢量S夹角α为太阳高度角，α∈(0°，90°)。太阳入射光线矢量S可表示为：

S=cosαcosω×I-cosαsinφ×J+sinα×K

(1)

式中:I、J、K分别为X、Y、Z轴方向单位矢量。

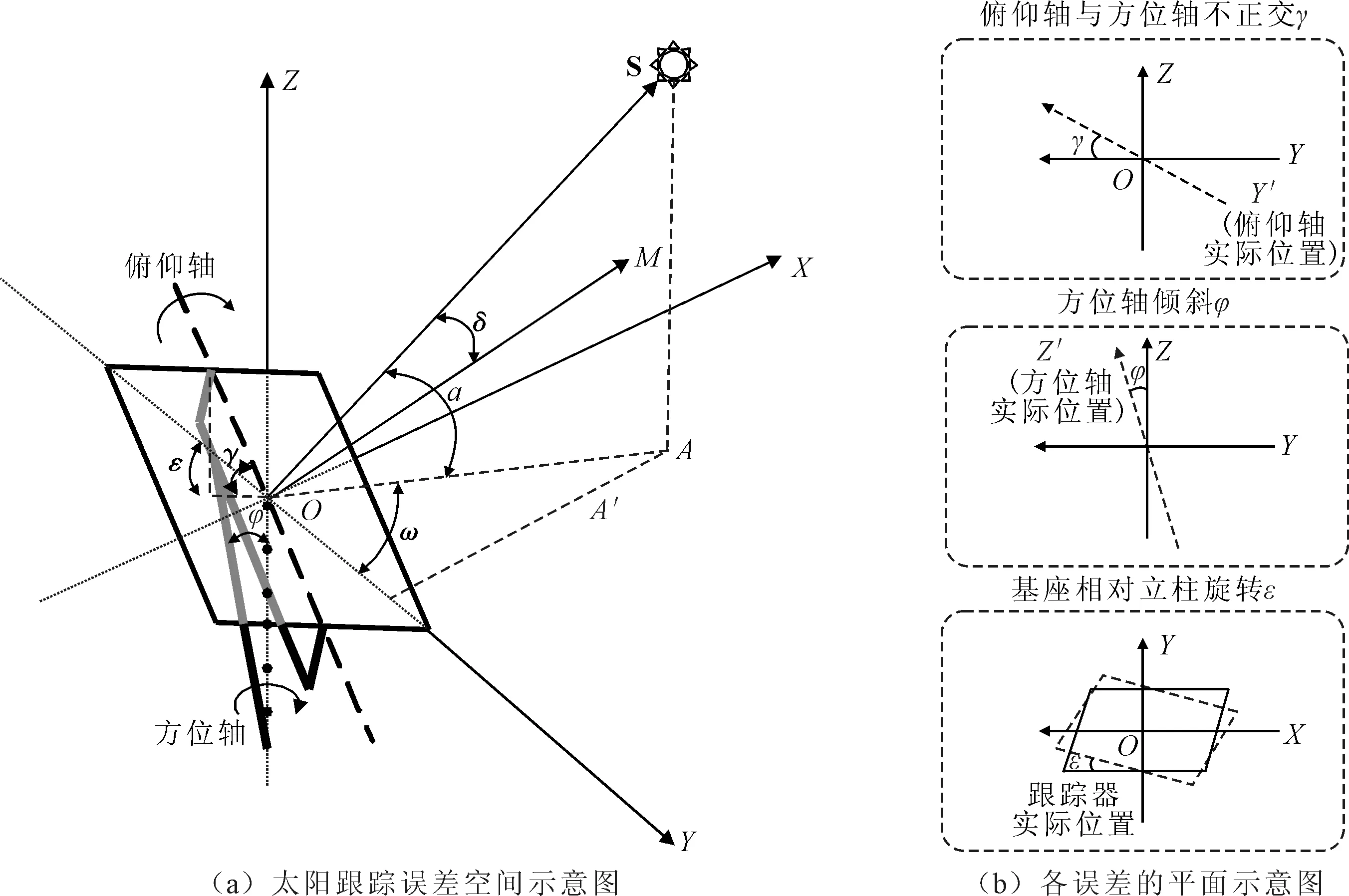
图1 跟踪误差模型示意图

图1(b)表示了误差源在模型推导过程中的一般处理方式。则φ、γ、ε可表示为：

[φ]=(cosφ+sinφ)×I+J+

(-sinφ+cosφ)×K

(2)

[γ]=I+(cosγ-sinγ)×J+

(sinγ+cosγ)×K

(3)

[ε]=(cosε-sinε)×I+

(sinε+cosε)×J+K

(4)

跟踪器指向矢量M为

M=[ε]·[γ]·[φ]·S

(5)

采用矢量夹角计算公式，跟踪误差角δ可表示为：

(6)

编码器零点偏移可以通过控制系统中加入偏差角补偿等[15],因此：

δ=F(φ、γ、ε、σ1、σ2、α、ω)

(7)

式中:σ1、σ2分别为方位角编码器和高度角编码器的零点偏移。

2 全局敏感性分析

Sobol方法是一种基于方差分解的模型独立全局敏感性分析方法，它可以处理非线性和非单调函数和模型。该方法的核心是将目标函数的总方差分解成单个参数及参数之间相互作用产生的方差。由前述得到模型可以表示为δ=F(φ、γ、ε、σ1、σ2、α、ω)，其中，δ为模型输出的目标函数；φ、γ、ε、σ1、σ2、α、ω为模型的参数。那么δ的方差D(δ)可作如下分解：

(8)

式中：D(δ)为模型总方差；Di为个体参数Fi单独影响的方差；Dij为参数Fi、Fj共同影响的方差；D123…n为n个参数共同影响的方差。

对上式(8)两端除以模型总方差D(δ),定义敏感度为:

S123…N=D123…N/D(δ)

(9)

S123…N为模型单个参数或参数之间相互影响的一阶或高阶敏感度，N=1,2，…,n，将式(9)代入式(8)，可得：

(10)

式中：Si为一阶敏感度，描述单个参数Fi在模型δ中所造成的影响；Sij为二阶敏感度，描述Fi和Fj两个参数共同作用对模型δ的影响；S123…n为n阶敏感度，表征n个参数共同作用对模型δ的影响。第i个参数的总敏感度为：

STi=∑S(i)

(11)

式中：S(i)为所有包含参数i的敏感度。

3 敏感度计算结果与讨论

3.1 静态敏感度

由于Sobol法的结果容易受到样本数量的影响，因此需要讨论样本数量对计算结果的收敛情况，以确保计算结果的可靠性。图2显示样本数量为2 100～21 000组过程中，一阶敏感度和总敏感度的收敛情况。由图2可知在样本数量为10 000组之后，计算结果仅有少量波动，敏感度趋于收敛。故采用10 000组样本数量作为计算，保证计算结果可靠。

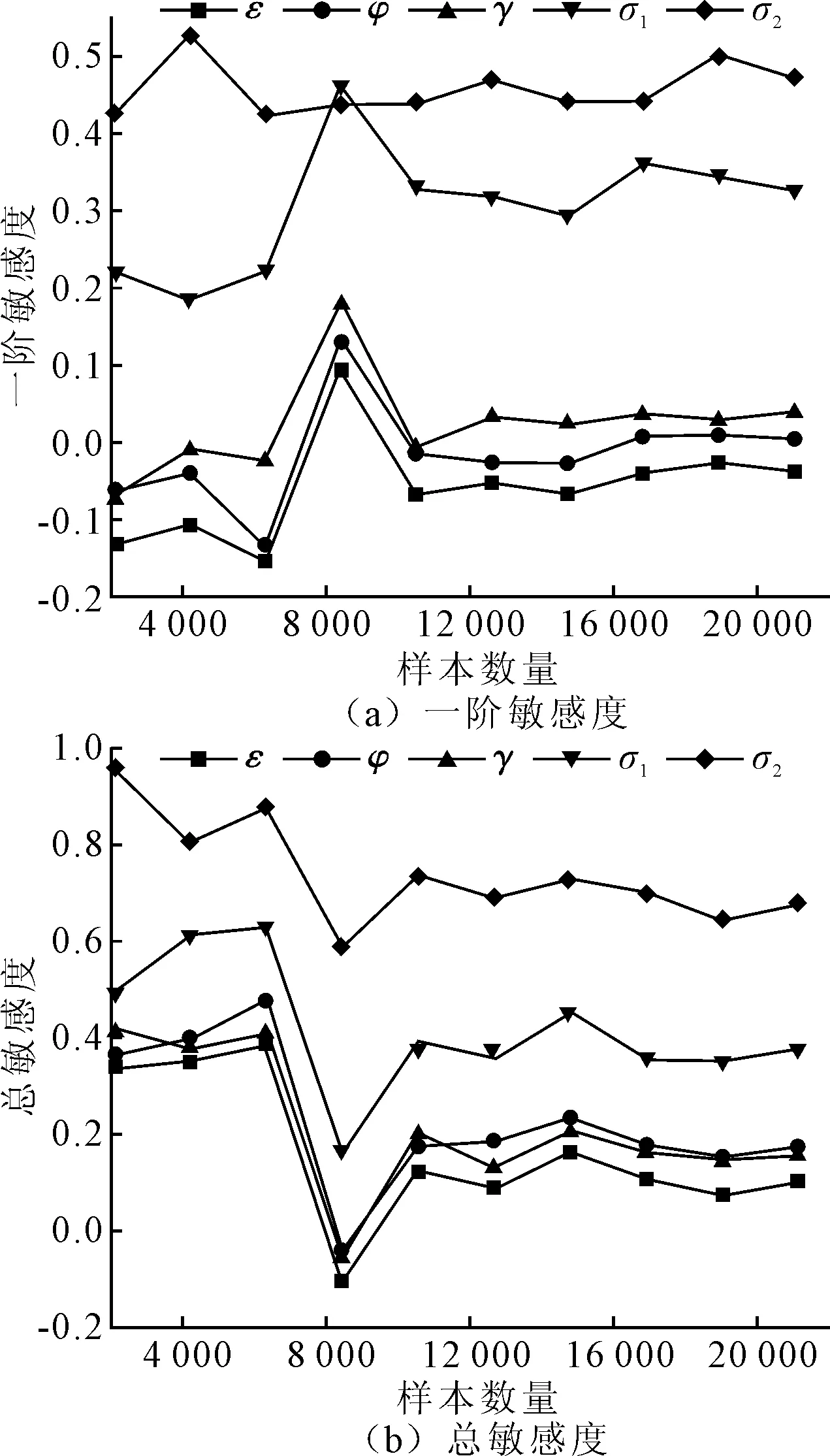
图2 Sobol法敏感度收敛过程

图3为各参数在夏至日的一阶平均敏感度和总平均敏感度。由图3可知ε、φ、γ、σ1和σ2的一阶平均敏感度分别为-0.014、0.091、0.012、0.400和0.401，总平均敏感度分别为0.046、0.218、0.071、0.375和0.551。通过敏感度计算结果可得如下结论：①方位角编码器零点偏移σ1约占30%，高度角编码器零点偏移σ2约占43%，表示跟踪误差主要受这2个参数的控制。②基座相对立柱旋转ε的敏感性较小，当参数自动校正时，可以固定该参数值提高校正效率和准确性。

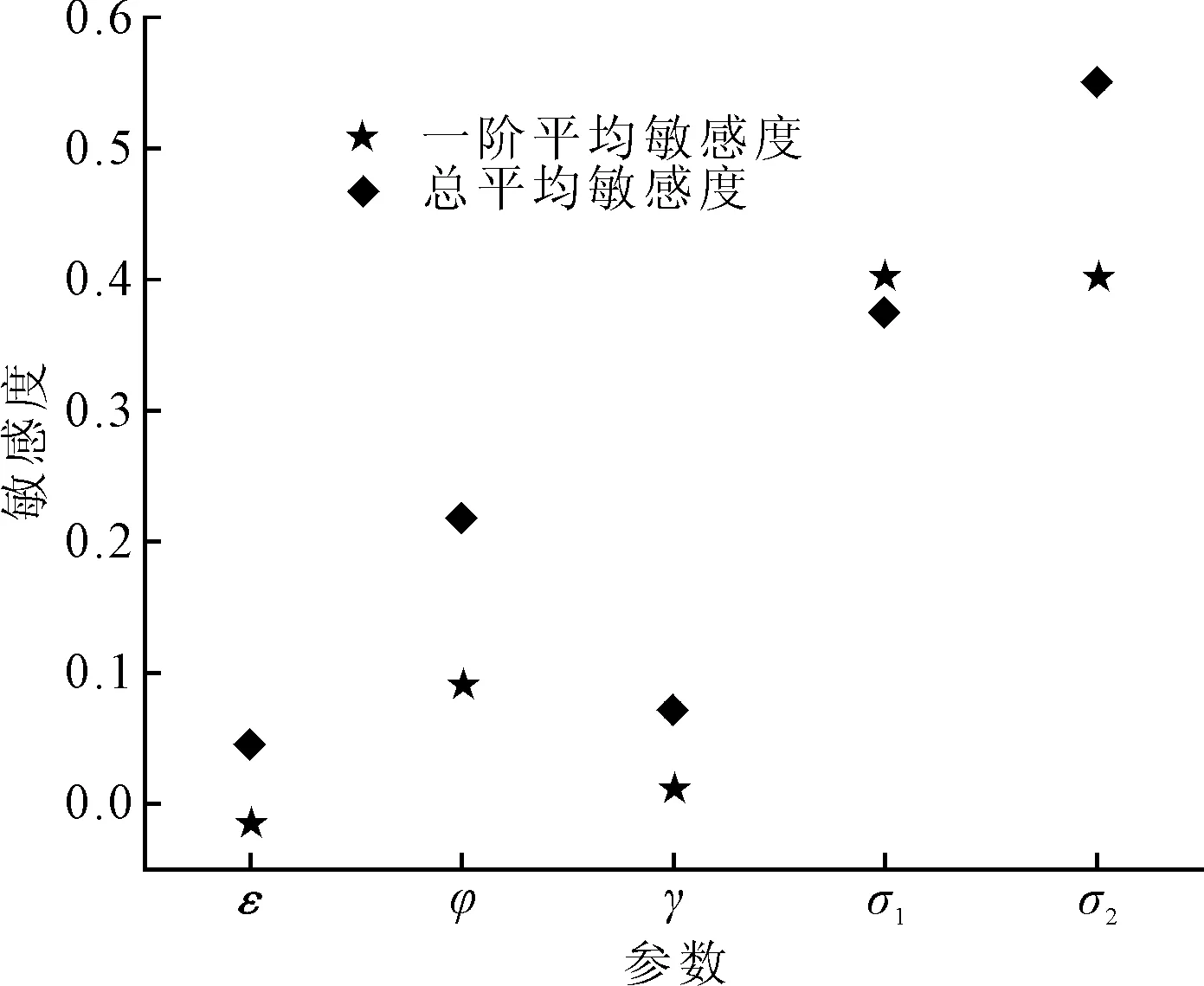
图3 Sobol法静态敏感度

3.2 动态敏感度

动态敏感性分析计算每个模拟时间步处的敏感度，能够观察随时间的变化模型参数对输出结果的影响，分析研究参数敏感性在不同时间段内的规律。图4(a)～图4(c)分别表示5个参数在夏至、秋分和冬至一整天时间一阶敏感度变化和总敏感度变化。计算结果表明：①所有参数在不同时间段的敏感度都有一定的变化，σ1、σ2平均敏感度明显大于其他3个参数，表明跟踪误差整体受这两个参数影响。②对于一阶敏感度，σ1敏感度先减小后增大，在中午达到最小值，σ2、φ敏感度先增大后减小，在中午达到最大值，而ε、γ敏感度相对比较平稳，只存在微小波动。③对于总敏感度，在时间上的总体变化规律与一阶敏感度类似，但在变化程度上有所不同，以σ2为例，夏至日ΔSi≈80%，ΔSTi≈18%。说明由于相互耦合作用，参数总敏感度变化较平稳。④由图4中中午时间段曲线斜率可以得知：对于不同日期，不同参数在中午时间变化速率为夏至>秋分>冬至，这是由于中午时间太阳轨迹在夏至日更接近坐标系天顶附近，太阳理论角度变化较快，在进行参数校正时，需要随时间变化调整。

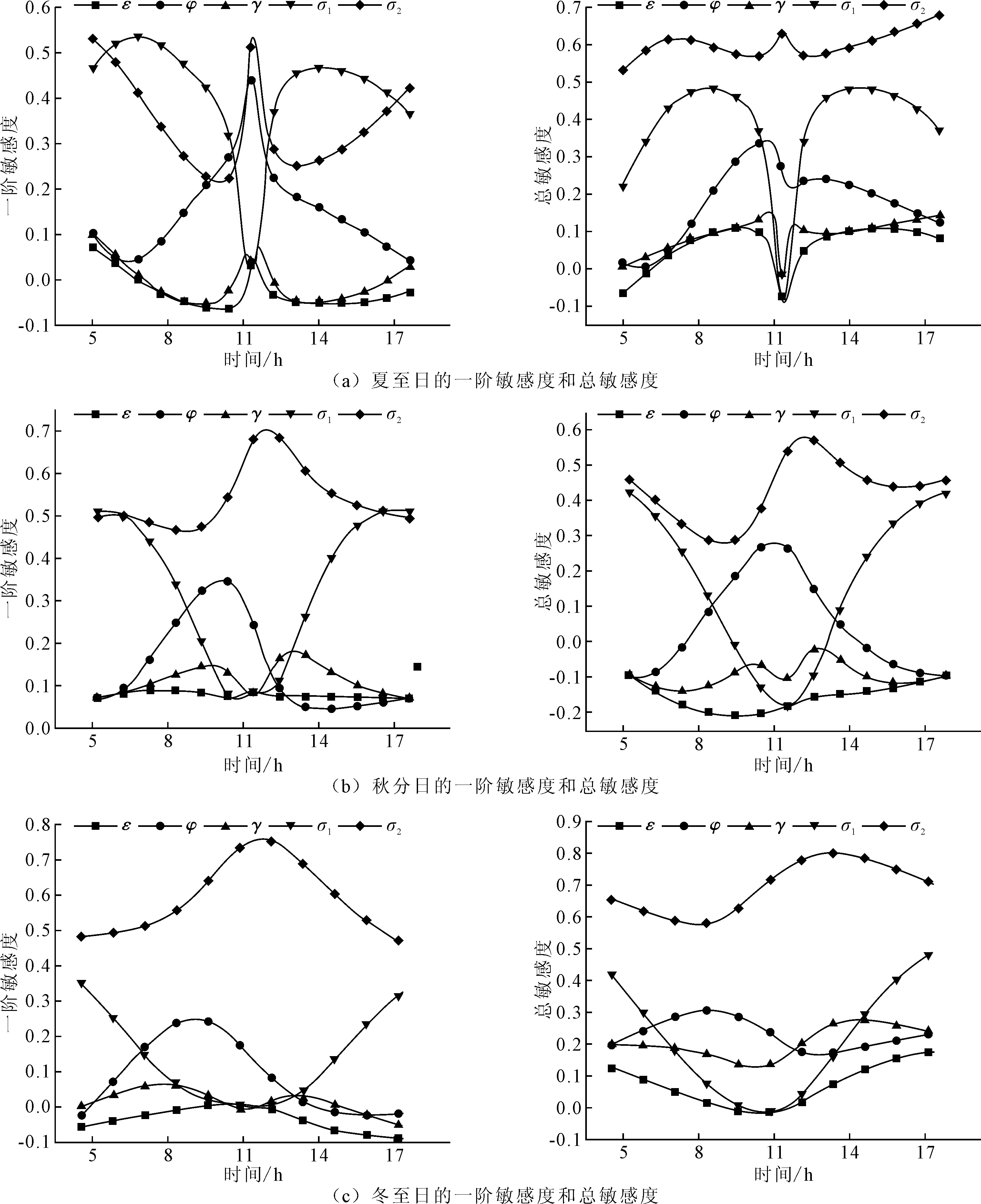
图4 动态敏感度分析

4 结论

笔者首先对太阳跟踪误差模型进行了推导，其次利用Sobol全局敏感性分析方法，以静态和动态的方式分别计算太阳跟踪误差模型中5个参数的一阶敏感度和总敏感度，得出以下结论：

(1)方位角编码器的零点偏移σ1和高度角编码器的零点偏移σ2这2个参数的敏感度显著高于其他参数，表示跟踪误差主要受这2个参数的控制；

(2)基座相对立柱旋转ε的敏感性较小，当参数自动校正时，可以固定该参数值提高校正效率和准确性；

(3)对于不同时间，各参数的敏感度不同，在中午时间段内，会出现不同程度的变化，且变化速率夏至>秋分>冬至，在进行参数校正时，需要随时间变化调整。