基于转矩脉动和径向力的定子极形优化

黄朝志　石王丰　郭桂秀　刘威

摘 要：由于开关磁阻电机有较大的振动和噪声，导致其在很多领域的应用受到限制。为了抑制振动，本文分析了电机振动产生的原理，分别从减小转矩脉动和径向力两方面出发，对原始模型进行了结构优化。首先，考虑到边缘磁通效应的影响，本文在定子齿顶部增添单侧极靴并进行磁导分析，通过调节气隙磁导以减小转矩脉动;在此基础上，依据麦克斯韦应力张量法，在定子齿弧面开设矩形槽，通过改善气隙磁密分布以降低径向力波峰值。有限元分析表明，该结构相对于原始模型，在平均转矩略微减小的情况下，实现了径向力波峰值和转矩脉动的降低。结合样机振动测试，进一步验证了该方案在减小振动上的合理性和可信度。

关键词：转矩脉动;磁导分析;气隙磁密;径向力波;定子开槽;定子极靴

DOI：10.15938/j.emc.2020.06.012

中圖分类号：TM 352文献标志码：A 文章编号：1007-449X（2020）06-0098-09

Optimization of stator pole shape based on torque ripple and radial force

HUANG Chao-zhi， SHI Wang-feng， GUO Gui-xiu， LIU Wei

（School of Electrical Engineering and Automation， Jiangxi University of Science and Technology，Ganzhou 341000， China）

Abstract：Because of the large vibration and noise of switched reluctance motor， its application is limited in many fields. In order to suppress high vibration， the principle of motor vibration is analyzed in this paper， and the structure of the original model is optimized by reducing torque ripple and radial force. Firstly， considering the influence of the edge flux effect， a one-sided pole shoe was added at the top of the stator pole and the analysis of the magnetic conductivity was carried out. The torque ripple can be reduced by adjusting the air gap magnetic conductivity. Furthermore， according to the Maxwell stress tensor method， a rectangular notch was obtained on the top of stator pole， and the peak value of the radial force wave was reduced by improving the air gap magnetic density distribution. The finite element analysis shows that compared with the original model， the peak value of radial force wave and the torque ripple is reduced with a slight decrease in average torque. The rationality and reliability of this method to suppress vibration are further verified by the vibration test of the prototype.

Keywords：torque ripple; analysis of magnetic conductance; air gap flux density; radial force wave; slotted on the stator; stator pole shoe

0 引 言

永磁同步电机用稀土永磁材料供量少、价格贵，且高温易失磁，所以，少用或不用永磁材料已成为电机发展趋势。开关磁阻电机（switched reluctance machine，SRM）定转子为双凸极结构，转子上没有绕组和永磁体，结构简单，调速范围宽，适用于高速运转，已成为一种极具竞争力的调速电机[1-2]。然而，SRM振动和噪音大，限制了在很多领域的应用与推广。现在，从电机结构和控制方法上研究减小SRM转矩脉动和径向力幅值已成为研究热点。

修改定转子极面形状以改变成非均匀气隙，或者增添定转子极靴都能减小转矩脉动。在传统8/6结构的SRM上，分别改变定子和转子的极弧中心和极弧长度，得到非均匀气隙，以减小转矩脉动[3]。通过改变转子极形状设计非均匀气隙以得到非对称电感曲线，一种两相的4/2极SRM结构被提出来[4]，该电机具有较宽的速度范围和低的转矩脉动。为了提高对称位置附近的转矩，文献[5]在定转子极顶各添加一个单侧极靴，通过改变磁通路径的方式来减小电机的边缘磁通效应，实现了转矩脉动的降低。通过多目标优化24/16混合动力汽车用SRM的关键参数，得出添加定子极靴降低了转矩脉动[6]。

在定转子极面或者侧面开槽也能改变电感的变化率，从而减小转矩脉动。文献[7-8]保持定子极不变，在转子一侧开三角形槽口，同时改变了自感和互感，使瞬时最小转矩增大而最大转矩变小。张鑫博士在转子的两侧开矩形槽口，基于改进磁场分割法计算气隙比磁导，从而验证了开槽能抑制径向力波[9]。

为了降低电机的径向磁吸力，文献[10]比较分析了传统SRM与互耦SRM，绕组方式不同引起磁路分布不一样，导致在相同条件下，互耦SRM的径向力比传统的要小1.5倍。最大径向力发生在定转子重叠时的电压关断位置，使定转子冲片叠压时沿轴向错开一定的斜角，从而在定子轭上分散径向力，也能达到减小径向力的目的[11]。一种双定子盘式结构电机（dual stator SRM，DSSRM）在文献[12]中提了出来，外定子和内定子的径向力分量在相反的方向上，相互抵消，而切向力在同一方向，相互叠加;文献[13]用多物理场分析方法比较了常规SRM和DSSRM，结构表明DSSRM不仅径向力幅值降低，而且分布更均匀化，振动更小。

本文主要从电机结构入手，分析转矩脉动和电机振动的主要原因，转矩脉动和径向力是电机振动的主要因素;并且分别从转矩脉动和径向力这两个思路进行探索，提出了定子单侧极靴与定子开槽的组合模型，进行参数优化，最后进行对比分析，论证了优化后的电机的合理性。

1 振动分析

电机运转过程中，定转子的电磁力可以分解为径向力分量和切向磁吸力分量。切向力产生输出转矩，其变化将引起转矩脉动;径向力将引起定子齿和定子轭的变形。这两个方向上受力状态的不断变化将引起振动和噪声。

首先，径向磁吸力主要产生在定子和转子齿重叠部分。根据麦克斯韦张力公式，径向分量比切向分量大很多，且在完全重叠位置，产生最大径向磁吸力。径向磁吸力随着步进式通电状态的变化而变化，造成定子铁心振动和变形。

其次，产生振动的另一因素是转矩脉动。由于开关磁阻电机的双凸极结构和各相依次通电的特点，导致电机换相期间的合成转矩具有周期性脉动特点，并造成大的噪音和振动。

切向磁拉力与转矩成正比例关系，两者按比例关系同步变化，转子上的转矩为

另外，由虚位移公式，当电流为常数，电磁转矩公式还可表示为

其中：W'为磁共能，W′=∫i0ψdi，ψ是磁链。可以看出，电感随位置角增长时为正转矩，随位置角降低时为负转矩，即制动转矩。在线性条件下，转矩和电流的平方成正比，与电流的极性无关。

2 转矩脉动分析

2.1 减小转矩脉动的方法

通常，定义的转矩脉动公式为

可以看出，抬高换相期间的最小转矩Tmin是减小转矩脉动的有效方法。SRM的最小转矩发生在转子换相区间[θon，θoverlap]的前半段，此时，前一相电流迅速衰减，电流减小;后一相转子在完全非对称位置附近，電感的变化率较低，根据式（3），总的合成转矩在此区间段达到最低。一种方法是保持关断角不变，提前开通导通角，在前一相电流关断之前，让后一相上升到一个较高的水平;二是合理地设计定转子极弧系数或添加极靴，以增加下一相的磁通量，从而增加最小转矩。

本文考虑通过第二种方法，即增添极靴形状和尺寸来改变磁通量的变化率。磁链ψ表示为

其中：P为磁导;N为线圈匝数。由此可知，在线圈匝数N，电流i一定的条件下，磁导P与电感L和磁通量成正比。当转子在[θon，θoverlap]区间向对称位置转动的过程中，通过调节磁导，增大磁通量，从而实现该区域转矩的提高。

2.2 定子极靴的增磁原理

为了提高定转子非重叠位置的磁导，本文提出了在与旋转方向相反的定子极一侧添加突出部分，类似于单侧极靴，以下称之为单侧极靴，结构如图2，旋转方向为逆时针。

将气隙磁场区域按图3所示进行划分，并令定子齿中心线与转子极间中心线对齐时为起始位置。本文仅考虑从起始位置到定子极后侧与转子极前侧相遇位置，即从β=0的位置到β=π6-βr+βs2位置期间的磁导。磁导分析如下：

k为确定椭圆的系数

其中：g为气隙长度;t为转子转过的弧长;β为转子转过的弧度;rr为转子半径。

利用椭圆半长轴半短轴长度的平均近似值，可以求出磁路的平均长度为

该区域的横截面积近似为

对应区域磁导的微分为

其中lstk为电机的轴向长度。

在不添加极靴的情况下，

其中：βr为转子极弧;βs为定子极弧。

该区域的总磁导为

添加单侧极靴后，

1）当定子极靴和转子极未重叠，即β≤π6-βr+βs2-βshoe时，

其中βshoe为极靴弧度。

设βshoe=π60，代入表1相关数据可得：

通过计算发现，从最大磁阻位置到定子极后侧与转子极前侧重合位置，添加极靴之后的磁导P1始终大于未添加极靴时的磁导P。通过增大该区域的磁导，可以有效提高该区域的电感，增多通过的磁链，最终提高了该区域的转矩，实现了最小转矩的提高。

2.3 减小转矩脉动的仿真

本文所采用的电机为8/6三相电机，其电机参数如表1所示。

为了找到极靴改变磁通量变化的最佳效果，通过有限元静态场仿真对单侧极靴不同角度α和高度H进行对比分析。保持H为1 mm不变的情况下，α依次选1°、2°、3°、4°、5°和6°。

在换相期间的前半段，随着模型极靴角的增加，相同的转子角位置有更高的电感，如图4（a）所示;当转子位置跨过极靴，到与初始模型的重叠角位置后，不同极靴角模型的电感又基本相同了。即，仅在极靴位置增加了电感变化量，增加了转矩;在转子运行到重叠角后，前期电感增量大的模型，后期的电感增量小了，所以转矩也小了，如图4（b）所示。

如图4（c）所示，随着极靴角度的增加，平均转矩接近于线性减小;同时最高转矩逐渐减小，其原因在于单靴模型可有效提高最小电感，但是对最大电感影响较小，从而降低了电感幅值变化率，造成最大转矩的下降。随着极靴角度的增加，转矩脉动先快速下降，并在4°时转矩脉动的降低效果减弱。当极靴角度大于4°时，定子极靴与转子重合过早，导致电感过早提高，从而使转矩上升过早，造成两相转矩衔接不及时，反而降低了最小转矩，加大了转矩脉动。

可以发现，极靴角度增大会在相同转子角位置提高最小电感，但也会造成定子开槽区间（即最小电感区）的缩小。如果此区间缩小过多，一是每一极电感增长区的电感幅值变化率减小，二是在定子转子位置重叠前，电流上升的时间短，电流幅值没有在此刻上升为最大，损失了电感率，平均转矩减小了。

考虑到需要在平均转矩和转矩脉动之间做权衡，本文选取了3°为最优角度。

确定角度为3°，极靴高度分别选为0.5、1、1.5和2 mm，并对模型进行有限元分析。

由图5可知，随着极靴高度的增加，平均转矩接近于线性减小，但转矩脉动的降低效果越来越差。综合考虑平均转矩和转矩脉动，选取1 mm为最优极靴高度。

综合以上，选择角度为3°、高度为1 mm的极靴尺寸作为最优尺寸。

需要注意的是，单靴模型反向转动的转矩波形与无极靴电机的转矩波形是一致。但是由于制动区间拉长，制动的平均转矩减小。

图6为单侧极靴模型与初始模型在不同电流下的电感对比，可以发现，单极靴模型在电流较小时可有效地提高电感，特别是在[θon，θoverlap]的前半段，将转矩提高到一个较高的位置，实现最小转矩的提高。当电流达到60 A后，磁场开始进入饱和阶段，相对于低电流时，电感减小，且当转子位置变化时，电感增加很小，本文的极靴效果也不明显了。

在额定转速1 500 r/min下，分別对初始模型和极靴角度3°、高度为1 mm的优化单极靴模型瞬态场仿真，如图7所示，该优化模型在平均转矩减小4.36%的情况下，降低了23.75%的转矩脉动。

3 定子极开槽的径向力分析

3.1 径向力减小的原理推导

根据虚位移公式，SRM的径向力为

其中：Wm为磁共能;g为气隙长度。在线性条件下，Wm可以写成

在磁路非饱和时，不考虑电流对电感的影响，则电感可以表示为

其中：N为线圈匝数;P为磁导

其中：lstk为电机定子叠片长度;r为定子内半径;βov为定转子重叠角度。在电流一定的情况下有下式关系：

由径向力公式（26），随着气隙长度的减小，即越到转子对称位置，径向力越大，负号表示径向力将使气隙长度越来越小;在定转子重叠后，若适当增大气隙长度，将有效降低径向力。这里在第3部分单向极靴优化模型基础上，在定子齿面开矩形槽，如图8所示，以实现径向力的减小，从而有效降低电机的振动和噪音。

3.2 定子极开槽尺寸对径向力的影响分析

选择对定子极顶中间开一个宽度为0.5 mm、深度为2.5 mm的槽口，并与未开槽模型进行对比。通过对断电时刻进行分析，得到图8所示的径向磁密、切向磁密的对比图，结果表明开槽模型在径向力波最大位置的径向磁密峰值降低了15.76%，切向磁密峰值提高了14.10%。

若降低径向磁密、增加切向磁密将实现径向力波的降低，图9（c）为断电时刻的径向力波对比图，验证了开槽模型能有效降低相应位置的径向力波。

保持槽口深度为1 mm不变，宽度依次选为05、1、1.5、2、2.5和3 mm，逐次对各模型进行有限元分析。

如图10（a）所示，随着开槽宽度的增长，平均转矩接近于线性减小。径向力从未开槽到开槽1.5 mm时，径向力波峰值逐渐减小，并且减小效果越来越弱;1.5～3 mm阶段径向力波峰值不降反增，其原因在于开槽宽度过大时，定子极顶饱和严重，部分磁链只能从开槽部分通过，导致径向磁密无法有效降低甚至出现增加，同时过宽的槽口也会导致漏磁增加，造成切向磁密减小，从而形成了径向力波峰值的这一变化。通过综合对比，选取0.5 mm为最优开槽宽度。

保持槽宽0.5 mm不变，深度依次选为0.5、1、1.5、2、2.5、3、3.5和4 mm，并进行有限元仿真。

如图10（b）所示，随着槽口深度的加深，0～3.5 mm时平均转矩逐渐下降，3.5 mm之后平均转矩小幅上升;0～3.5 mm深度时径向力波峰值逐渐下降，3.5 mm之后径向力波峰值不降反增。通过对平均转矩径向力波峰值的综合对比，考虑到2.5～3 mm的过程平均转矩下降幅度比径向力波峰值下降更明显，选取深度2.5 mm为最优值。相对于未开槽的极靴模型，该模型在平均转矩降低4.08%的情况下，实现了径向力波峰值30.77%的降低。

可以发现，开槽过大会导致定子饱和程度进一步提高，更多的磁链无法通过定子极，从而造成平均转矩的较大损失;而开槽过小会导致效果不明显，无法有效地降低径向力。

4 性能对比

综合第2部分和第3部分，本文的最终优化模型为：在定子中间开一个宽0.5 mm、深2.5 mm的槽口，同时在与旋转方向相反的定子极侧加一个角度为3°、高度为1 mm的极靴。

在转速为1 500 r/min，导通角和关断角一致情况下进行仿真实验，图11为最终模型与原始模型的转矩对比和径向力对比图。随着位置角的变化，在定转子重合前，径向力处于缓慢增加的状态;当定转子部分重叠时，产生有效转矩的切向力逐渐减小，径向力逐渐增加，到断电时刻电机产生径向力峰值;随后，由于电流快速减小，径向力随之快速下降。

相对于原始模型，最终模型的优化效果为：在平均转矩减小8.54%的情况下，径向力波峰值下降了34.52%，转矩脉动下降了43.39%。

5 实验验证

5.1 样机测试系统

为了进一步验证模型的有效性，本文依照表1的关键参数制造了2台样机，分别是未开槽无极靴的开关磁阻电机A，和开槽且有单侧极靴的开关磁阻电机B，样机实物图如图12所示。

样机测试系统包括AD1000T-D型加速度传感器（1 000 mV/g）、MPS-140801型号的数据采集卡（采样频率为64 kHz）、SRD7.5-1500型号开关磁阻电机控制器、被测开关磁阻电机和电脑等，如图13所示。

5.2 振动测试结果

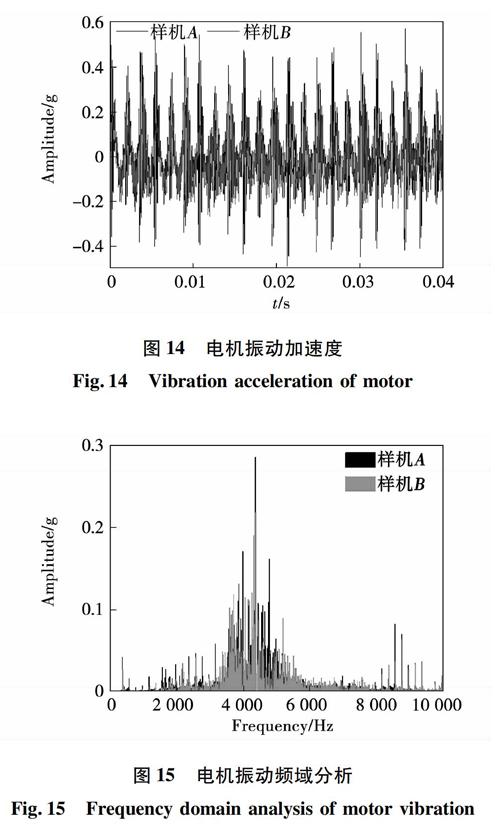
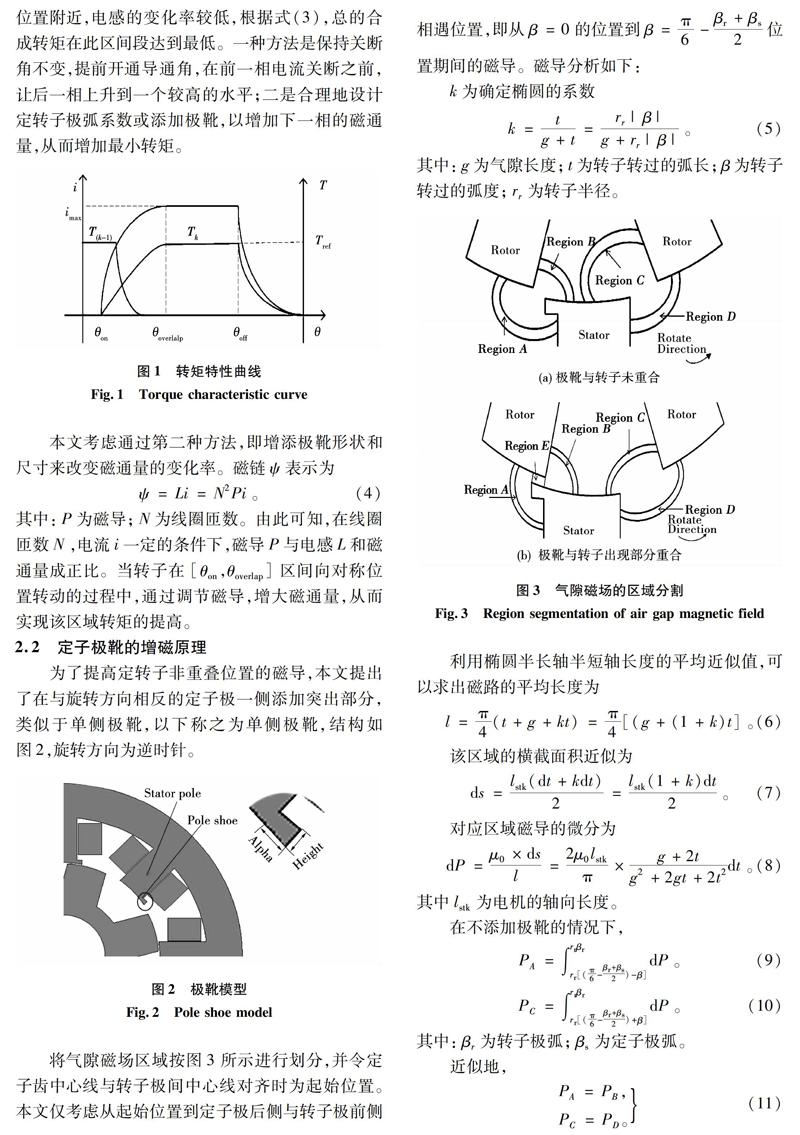
在对准定子的外壳部分，选取居中位置，安装振动加速度传感器，从而实现对电机振动加速度的测量。设定电机转速为1 500 r/min，测得数据如图14、图15所示。

如图14所示，样机A的最大振动加速度为0571 8 g，样机B的最大振动加速度为0.428 5 g，样机B的最大振动加速度要比样机A小25.06%。对实验数据进行傅里叶分析，得到电机的频域分析对比图，如图15所示，样机A和B在3 000～5 000 Hz之间取得较高的振动加速度，且样机B在该频率段的振动加速度幅值明显小于样机A。实验结果表明，样机B对于振动加速度有较好的改善效果，即最终模型相对于初始模型有较好的减振效果。

6 总 结

本文通过分析电机振动的主要原因，从切向方向上的转矩脉动和径向方向上的径向力出发，综合优化，提出了一种新型定子结构，该定子是通过在与旋转方向相反的定子极侧增添角度为3°、高为1 mm的单侧极靴，同时在定子弧面开一个深度为2.5 mm、宽度为0.5 mm的槽口而得来的。通过有限元仿真分析，得到如下结论：

1）相对于常规模型，单侧极靴可以有效地提高定转子非重叠区域的电感，将该区域转矩提前提高到一个较高的位置，拉高了两相交换区域的最小合成转矩，实现转矩脉动的降低。

2） 通过对定子弧面开槽，有效地實现了径向力波峰值的降低。但随着开槽宽度的加大，平均转矩也出现了明显的降低。综合考虑平均转矩和转矩脉动，确定了最终的优化尺寸。

参 考 文 献：

[1] 朱曰莹，杨传甜，赵桂范，等.电动车用开关磁阻电机驱动系统多指标同步优化[J].电机与控制学报，2018， 22（010）：25.

ZHU Yueying， YANG Chuantian， ZHAO Guifan， et al. Optimization of the switched reluctance motor drive system in electric vehicles application[J]. Electric Machines and Control， 2018，22（010）：25.

[2] 曲兵妮， 宋世潮， 宋建成， 等. 考虑小电感区电感变化量的开关磁阻电机开关角优化方法[J]. 电机与控制学报， 2019， 23（02）：91.

QU Bingni， SONG Shichao， SONG Jiancheng， et al. Switch angle optimization method for switched reluctance motor considering the inductance variation[J]. Electric Machines and Control， 2019， 23（02）：91.

[3] Mousavi-Aghdam S R， Feyzi M R， Ebrahimi Y. A new switched reluctance motor design to reduce torque ripple using finite element fuzzy optimization[J]. Iranian Journal of Electrical & Electronic Engineering， 2012， 8（1）：91.

[4] Lee D H， Pham T H， Ahn J W. Design and operation characteristics of four-two pole high-speed SRM for torque ripple reduction[J]. IEEE Transactions on Industrial Electronics， 2013， 60（9）：3637.

[5] 李哲， 郑玲， 杨威， 等. 开关磁阻电机转矩脉动及结构优化设计研究[J]. 电机与控制学报，2018， 022（6）：11.

LI Zhe， ZHENG Ling， YANG Wei， et al. Research on torque ripple and structure optimization of switched reluctance motor[J].Electric Machines and Control， 2018， 022（6）：11.

[6] JIANG J W， BILGIN B， EMADI A. Three-phase 24/16 switched reluctance machine for a hybrid electric powertrain[J]. IEEE Transactions on Transportation Electrification， 2017， 3（1）：76.

[7] LI GUANGJIN， OJEDA J， HLIOUI S， et al. Modification in rotor pole geometry of mutually coupled switched reluctance machine for torque ripple mitigating[J]. IEEE Transactions on Magnetics， 48（6）：2025.

[8] LEE J W， KIM H S， KWON B I， et al. New rotor shape design for minimum torque ripple of SRM using FEM[J]. IEEE Transactions on Magnetics， 2004， 40（2）：754.

[9] 张鑫， 王秀和， 杨玉波. 基于改进磁场分割法的开关磁阻电机径向力波抑制能力解析计算[J]. 电工技术学报， 2015， 30（22）：15.

ZHANGXin， WANG Xiuhe， YANG Yubo. The computation of vibration reduction capacity for switched reluctance motor based on improved magnetic field partition method[J].Transactions of China Electrotechnical Society，2015，30（22）：15.

[10] LIANG X， LI G， OJEDA J， et al Comparative study of classical and mutually coupled switched reluctance motors using multiphysics finite-element modeling[J]. IEEE Transactions on Industrial Electronics， 2014， 61（9）：5066.

[11] YANG H Y， LIM Y C， KIMH C. Acoustic  noise/vibration reduction of a single-phase  SRM using skewed stator and rotor[J]. IEEE Transactions on Industrial Electronics， 2013， 60（10）：4292.

[12] ASGAR M， AFJEI E. Radial force reduction in a new flat-type double-stator switched reluctance motor[J]. IEEE Transactions on Energy Conversion， 2016， 31（1）：141.

[13] ISFAHANI A H， FAHIMI B. Comparison of mechanical vibration between a double-stator switched reluctance machine and a conventional switched reluctance machine[J]. IEEE Transactions on Magnetics， 2014， 50（2）：1.

（編辑：刘素菊）

收稿日期： 2018-12-31

基金项目：国家自然科学基金（51767009）

作者简介：黄朝志（1978—），男，博士，研究方向为开关磁阻电机结构优化设计、振动与噪声抑制;

石王丰（1994—），男，硕士研究生，研究方向为开关磁阻电机本体设计;

郭桂秀（1991—），女，硕士研究生，研究方向为开关磁阻电机本体设计;

刘 威（1996—），男，硕士研究生，研究方向为开关磁阻电机振动与噪声抑制。

通信作者：石王丰