基于ARIMA与神经网络的备件需求组合预测方法
王 宁 ,李建华 ,王军军 ,李双雪 ,唐 宁
(1.兰州理工大学机电工程学院,甘肃 兰州 730050;2.兰州兰石集团有限公司铸锻分公司,甘肃 兰州 730050)
备件在保障设备正常使用和维修任务中占据重要地位,备件的消耗受到使用环境、设备维护、备件使用寿命等多种因素影响,预测难度较大。基于时间序列进行的预测容易理解与应用,预测精度较高[1]。精确的备件需求预测能够优化库存结构,降低库存管理难度,减少资金占用,因此科学的预测技术是非常重要的。
现有的时间序列预测技术包括统计方法和机器学习两大类[2],统计方法以差分自回归移动平均(ARIMA)模型[3-5]为代表,而机器学习方法以神经网络、支持向量机等为代表。韩梅丽[6]等以需求量波动较大的备件为研究对象,采用ARIMA时序模型对备件时序消耗做出了预测。丁红卫[7]等通过所需设备的历史数据对构建BP神经网络模型进行训练,将训练好的模型用于电网物资的需求预测。有学者将LSTM与卷积神经网络融合,并运用于预测、语音识别等领域[8,9],李梅[10]等提出基于注意力机制的CNN-LSTM模型,运用于热电联产供热的预测,对比支持向量机、LSTM单一预测模型,该组合模型取得了更好效果。
但是ARIMA仅适用于线性时间序列的预测,而神经网络适用于非线性系统的预测,基于ARIMA和神经网络在时间序列预测方面各自的优劣势,本研究提出一种基于ARIMA、BP神经网络和卷积长短期记忆神经网络的组合模型 (ARIMA-BP-CNN),充分提取时间序列数据的线性和非线性特征,应用该模型对备件需求量做预测,并通过电解铝企业天车某备件的消耗情况进行验证。
1 基本理论
1.1 ARIMA时间序列模型
差分自回归移动平均模型,记作ARIMA,是一种时间序列预测分析方法。ARIMA(p,d,q)中,AR为自回归,MA为移动平均,p是自回归项数,q是移动平均项数,d是保障差分后得到平稳序列数据的差分次数。时间序列模型是基于历史数据建立起来的模型,以p、d、q为参数的ARIMA模型可表示为:

其中:Xt为时间序列的样本值,φi(i=1,2,…,p)和θi(i=1,2,…,q)为模型参数,εt为独立正态分布的白噪声。
ARIMA模型首先要对时间序列做一次或者多次差分,转换成平稳时间序列,再进行建模分析。ARIMA模型对时间序列数据的线性相关性预测精度高,但对分线性关系处理效果欠缺。
1.2 BP神经网络
BP神经网络是20世纪80年代提出的误差反向传播算法,BP神经网络网络由输入层、隐藏层和输出层组成,隐藏层可以是一层或多层,本文训练的是隐藏层为一层BP神经网络,如图1所示。BP算法分为前向传播和反向传播两个部分,前向传播是输入信息从输入层传入,经中间的隐藏层最终传至输出层,若获得预期的输出结果,则学习过程终止;否则,它将转向反向传播。反向传播是与原始连接路径反方向,通过误差逐层修改网络权值及阈值,再将更新的权值和阈值正向传播,通过正向、反向传播的循环进行得到最优权值和阈值。
隐藏层与输入层关系:

其中,θj为隐藏层第j个神经元的阈值,wij为输入层和隐藏层的连接权值,netj是第j个神经元的激活值,yj是隐藏层的输出值,f为激活函数,通常是Sigmoid函数。输出层和隐藏层与上述关系类似,激活函数通常为线性函数。
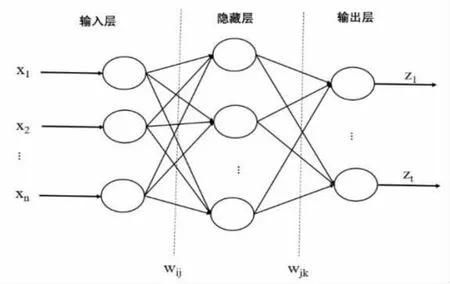
图1 三层BP神经网络结构
1.3 卷积长短期记忆神经网络
1.3.1 卷积神经网络
卷积神经网络 (Convolutional Neural Networks,CNN)是一种具有深度结构的前馈神经网络,由输入层、卷积层、池化层、全连接层以及输出层组成。卷积神经网络可以有多个卷积层与池化层,二者交替使用从原始数据中获得有效表征,提取数据的特征,然后经过全连接层解除多维结构,最后到达输出层,完成分类、预测等任务。
1.3.2 长短期记忆网络
LSTM是一类特殊的递归神经网络,它克服了传统递归神经网络存在的梯度爆炸和梯度消失的问题,适合处理和预测时间序列事件。如图2所示,每个LSTM由输入门、忘记门、输出门和细胞状态组成,更新方式如下:
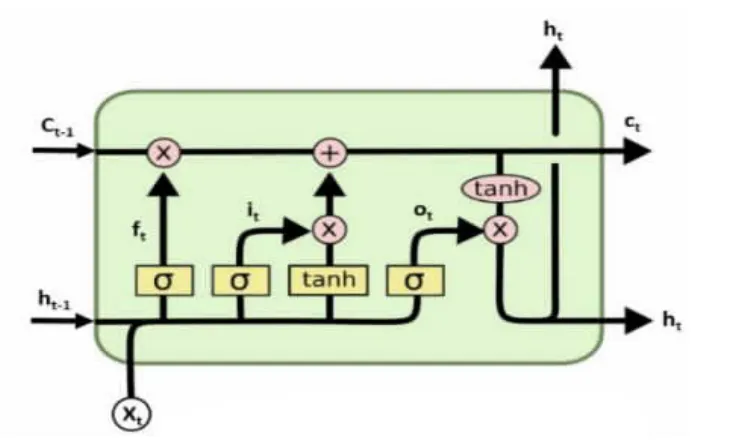
图2 LSTM网络基本单元

其中,ft、it、Ct、ot分别表示忘记门、输入门、细胞状态和输出门;bf、bi、bc、bo分别表示不同门对应的偏置;Wf、Wi、Wc、Wo分别表示不同门对应权值;xt表示当前节点的输入;ht表示当前节点的输出;σ表示激励函数Sigmoid;G^t表示计算过程中的候选值向量。
1.3.3 CNN-LSTM神经网络
CNN-LSTM神经网络算法由三部分组成。第一层,将原始数据热向量编码,使其映射为k维空间,得到新特征。第二层,将新特征输入卷积神经网络,设置若干对卷积层和池化层,提取数据特征。第三层,将CNN的输出数据作为LSTM神经网络的输入,做时序的预测,如图3所示。

图3 CNN-LSTM模型
2 组合预测模型
2.1 ARIMA-BP-CNN组合预测方法数学模型
传统的预测方法以及机器学习算法均有其局限性,单一的方法不能得到理想的预测结果,文章采用组合预测方法对备件需求进行预测。Armstrong分析表明,组合预测方法对短期问题的预测更有效,预测结果的精确度更高[11]。组合预测理论中,若存在n种解决实际问题的预测方法,那么可以能通过给这n种方法分别赋予适当的权重,再将n种方法的预测结果分别乘以对应的权重,各项累加,进而得到组合模型的预测结果。
假设某项预测问题在观测时段的实际值为yt(t=1,2,…,m),对于该问题的n种预测模型中,各自的预测值为 git(i=1,2,…,n; t=1,2,…,m),各预测模型的权重系数为wi(i=1,2,…,n)。于是组合模型的预测值t表示为:
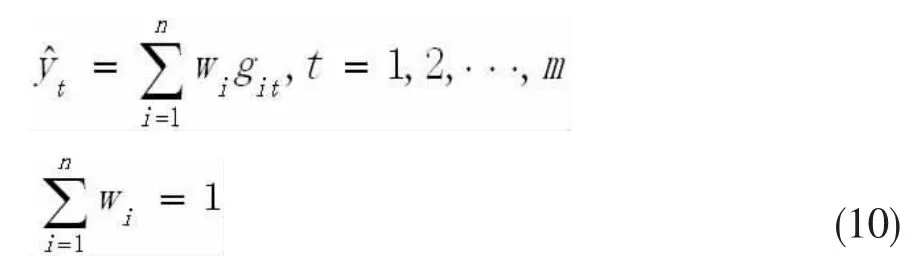
进而得到组合预测的误差:
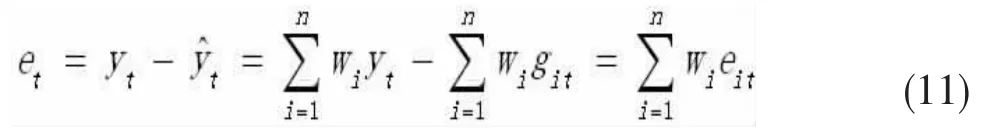
文章结合前面介绍的ARIMA、BP神经网络和卷积长短期记忆神经网络,将三种方法结合,组成新组合预测方法(ARIMA-BP-CNN)。于是公式(9)的形式为:

2.2 ARIMA-BP-CNN方法预测步骤
应用该组合预测方法进行预测,得到较高精度的预测结果,关键是确立各单一模型的权重系数,本文采用遗传算法优化ARIMA-BP-CNN模型的权重系数。图4是本文提出的ARIMA-BP-CNN组合模型流程图,该组合预测方法步骤如下:
步骤 1:分别使用 ARIMA、BP神经网络和CNN-LSTM对原始时间序列数据进行预测,得到单一模型的预测结果。
步骤2:为各单一模型分配初始权重,分别用步骤1各方法的预测结果乘以对应的权重,各项累加,得到ARIMA-BP-CNN模型的预测结果。
步骤3:采用遗传算法优化权重系数。初始权重未必能得到预期的结果,使用遗传算法对组合模型的权重加以优化。
步骤4:精度的预测。若组合模型得到期望的预测精度,进行步骤5;否则,返回步骤2继续采用遗传算法优化权重系数,直至得到期望的预测精度。
步骤5:输出组合模型的预测结果,如图4所示。

图4 基于ARIMA、BP和CNN的组合预测流程图
3 实例分析
现有2010年至2018年间某电解铝企业天车某备件消耗数据,以季度为时间单位统计了36个历史消耗数据,详细见表1.在这36个历史数据中,选择前32个作为训练数据,后面4个作为检验数据。
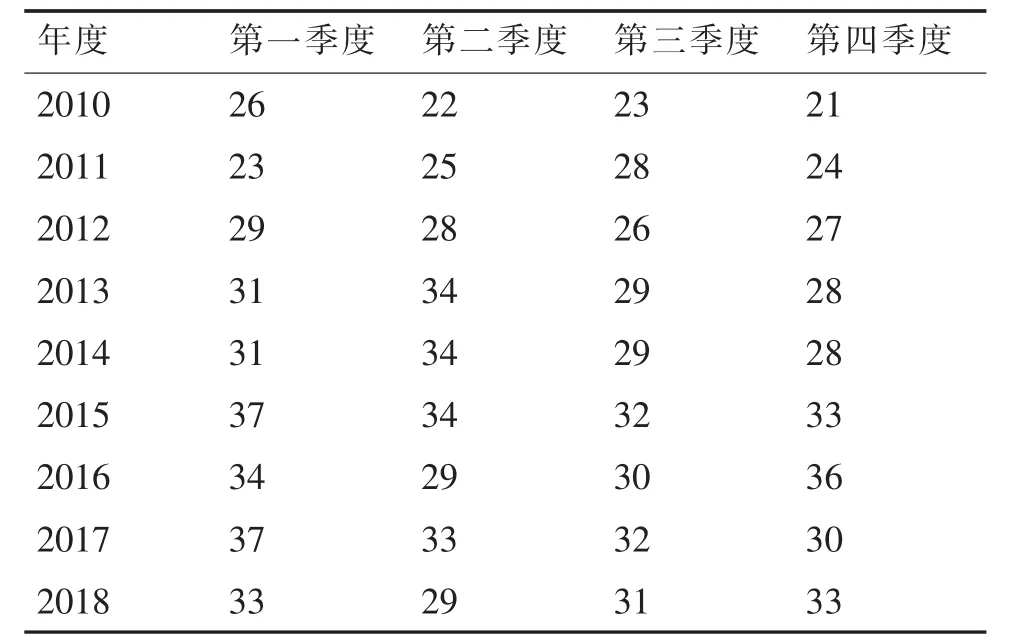
表1 某备件消耗数据
3.1 ARIMA时间序列预测
将2010年至2017年的32个消耗数据作为输入数据,得到2018年四个季度该备件消耗的预测结果。
(1)检验序列的平稳性。

图5 备件消耗不平稳序列图
图5时序图显示该序列具有曲折上升的趋势,可以判断为非平稳序列;单位根检验统计量对应的p值为0.11487显著大于0.05,最终判断该序列为非平稳序列。
(2)对原始序列一阶差分,并进行平稳性和白噪声检验。
图6显示,一阶差分后的序列时序图在均值附近比较平稳的波动;图7显示,自相关图有很强的短期相关性;单位根检验p值为0.04小于0.05;白噪声检验p值为0.02小于0.05,所以一阶差分后的序列为平稳非白噪声序列。
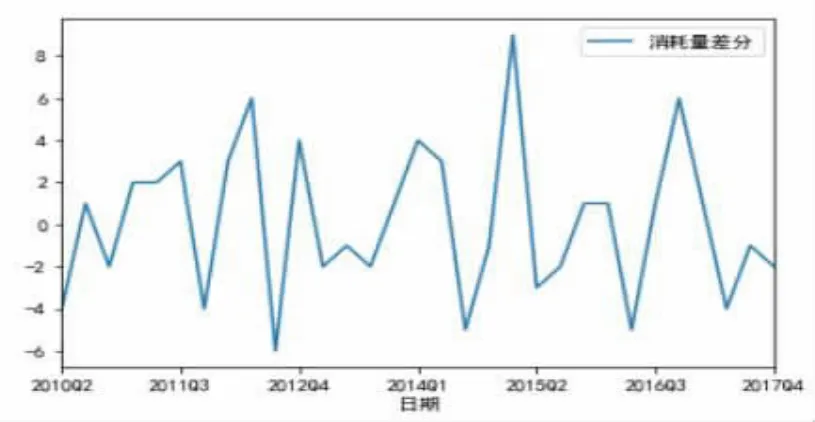
图6 备件消耗平稳序列图

图7 备件消耗ACF图
(3)对差分后的序列拟合ARIMA模型。
计算ARMA(p,q)。计算p和q均小于等于3的所有组合的BIC信息量,取其中BIC信息量最小的模型阶数。计算结果显示p值为0、q值为1时最小BIC 值为 166.2731,因此 p、q 定阶 0、1。
(4)ARIMA模型预测。
应用ARIMA(0,1,1)对该备件2018年四个季度(Q1-Q4)需求量做预测,预测结果见表2。
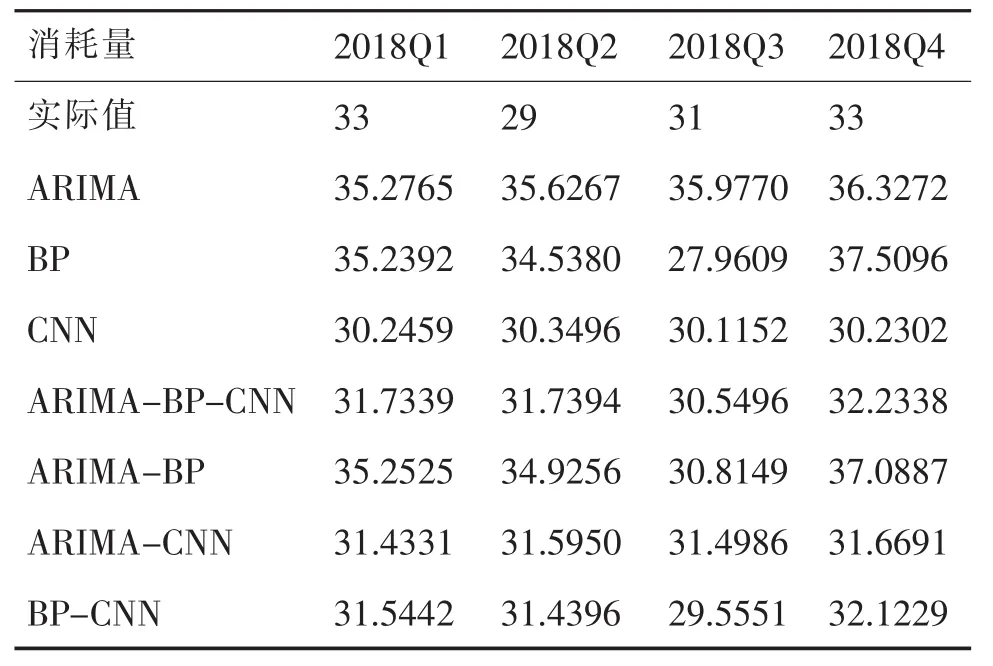
表2 备件实际消耗量与各模型的预测值
3.2 BP神经网络预测
将该备件的历史消耗数据,依次从第1个数据开始,紧邻的8个作为神经网络的输入,第9个数据作为待预测的消耗值,即神经网络的输出,将这9个相邻的历史数据作为1个样本。将前32个数据作为训练数据集,按此方法得到24个样本,用来训练BP神经网络。输入层有8个单元,输出层有1个单元,取隐藏层8个单元,relu作为激活函数,训练该BP神经网络,学习5000次后,用这个训练好的BP神经网络模型对2018年四个季度该备件的消耗量做预测,预测结果见表2。
3.3 CNN-LSTM神经网络预测
将该备件的历史消耗数据,依次从第1个数据开始,紧邻的4个作为神经网络的输入,第5个数据作为待预测的消耗值,即神经网络的输出,将这5个相邻的历史数据作为1个样本。将前32个数据作为训练数据集,按此方法得到28个样本,以此训练深度学习神经网络。输入层为4个单元,依次通过卷积、池化、LSTM层、Flatten等过程,输出层为1个单元,relu作为激活函数,mae作为损失函数,对神经网络进行训练,学习1000次后,用这个训练好的CNN-LSTM模型对该备件2018年四个季度的消耗量做预测,预测结果见表2。
3.4 组合预测
(1)确定权系数
以误差平方和最小作为模型组合的最优准则,建立如下广义误差最小的组合预测权重确定模型:

运用遗传算法确定该非线性问题的权重,将目标函数作为遗传算法的适应度计算值,使用MATLAB中的GA工具箱调用该函数进行计算,通过反复实验,得到三种方法对应的权值:

(2)组合模型做预测
通过公式(14)计算得到组合模型预测值,结果见表2。

另外,为进一步比较三种方法组合模型的预测精确度,同样计算了单一方法的两两组合预测结果,以误差平方和最小作为模型组合的最优准则,使用相同方法计算得到ARIMA-BP的组合权重为:w1=0.356,w2=0.644;ARIMA-CNN 的组合权重为:w1=0.236,w2=0.764;BP-CNN 的组合权重为:w1=0.26,w2=0.74。两两组合方法的预测结果见表2。
3.5 结果分析
文章提出的ARIMA-BP-CNN方法是综合三种不同方法的新方法,结合三种方法的过程中,对每一种方法进行加权,其中CNN的权重系数最高,对组合方法的贡献最大。
为了直观显示单一方法和组合方法的预测精度,将备件消耗的实际值减去各方法的预测值,得到图8的误差曲线图。从图中可以看出ARIMABP-CNN方法的整体误差最接近于零,其他三种方法只有第二季度CNN有较小的误差,其他季度里三种单一的方法都具有较大的误差。

图8 四种预测方法的误差曲线
为进一步说明预测结果的有效性以及改进后组合模型的提升效果,从均方根误差(RMSE),平均绝对误差(MAE),平均绝对百分比误差(MAPE)这3个方面进行对比分析,具体见表3。

表3 预测效果评价表
从表3可以看出,ARIMA-BP-CNN方法的评价指标均低于三种单一方法的评价指标,其中,相比于ARIMA方法,ARIMA-BP-CNN将RMSE降低了65.9%,将MAE降低了69.6%,将MAPE降低了69.5%,预测精度取得了较大提升。
两两组合模型中,ARIMA-BP方法的预测精度相对偏低,ARIMA-CNN和BP-CNN的预测精度相对较高,但仍低于组合预测模型ARIMA-BP-CNN的预测精度。
综上所述,ARIMA-BP-CNN组合预测模型的预测精度最高,优于三种单一预测方法。
4 结束语
针对电解铝企业的备件需求预测问题,构建了基于ARIMA、BP神经网络和深度学习CNN-LSTM神经网络三种方法的组合预测模型,解决了备件消耗的预测问题,充分发挥了ARIMA解决线性问题的能力和神经网络解决非线性问题的能力,摆脱了单一预测方法的弊端,通过电解铝企业天车某备件为实例,验证了该组合模型在备件需求预测中的可行性与精确性。

