五模块浮车型有轨电车的轮重调整模型
于 倩,刘 劲
(中车株洲电力机车有限公司产品研发中心,湖南 株洲 412001)
1 研究背景及意义
在城市轨道交通车辆的设计流程中,重量管理是总体设计不可轻视的一部分。其中轮、轴重参数尤为重要,各轮对重量分配以及各轴的轴重偏差是否均衡,直接影响到车辆黏着牵引力的发挥和牵引性能的优劣,从而影响到车辆的运行稳定性、安全性等[1]。对于采用悬挂的城轨车辆,调整轮、轴重主要采用加垫调簧方法,无论是对一系悬挂还是二系悬挂的承载进行调整,都可以影响整个车辆的轮、轴重分布[2]。
现有车辆轮重偏差控制工艺将转向架与车体分开进行控制,转向架与车体重量分配分别满足要求后,进行转向架与车体装配,整车组装完成后再对准备状态下的车辆进行轮重偏差调整,最终确保整车轮重偏差合格。这种称重调节方式的优点在于计算方式简单,具有较高的计算速度,能够根据传感器准确及时地获得各个轮重的大小。但该称重调平方法在实际应用过程中,现场添加调整垫片时,更多的是根据经验,凭人工通过多次调整达到理想效果,工作流程重复,工作量大[3]。
基于以上背景及现状,本文针对城轨新产业中市场份额较大的有轨电车,根据转向架和车体的结构特点简化受力情况,建立弹簧加垫调整车轮载荷的模型;然后通过表格法建立调整车轮载荷的系统刚度矩阵;由此计算出弹簧加垫的外力矢量矩阵;最后求解弹簧加垫的系统方程,得出加垫后的轮重情况,为后续实现计算机程序指导轮重偏差调整奠定了基础。
2 有轨电车简化模型分析
有轨电车的车辆结构形式主要分为单车型、浮车型、铰接型和单、浮车组合型[4],常见的主要是单车型和浮车型,如图1和图2所示。

图2 五模块浮车型有轨电车编组图
有轨电车由于其模块间铰接装置的特性,在称重时要求整列车连挂好后一起称重。当试验台长度不允许时,可在自由铰处将列车分为2部分分别称重。以下以五模块储能式有轨电车为例说明。
五模块多铰接有轨电车采用“=Mc1+F1+Tp+F2+Mc2=”编组。Mc1、T、Mc2模块各配置1台转向架,转向架采用独立轮型式。各模块间通过铰接装置连接,车辆下部采用固定铰,固定铰具有3个方向转动自由度。车辆上部采用弹性铰和自由铰,弹性铰可以实现连接车辆间3个方向的转动自由度,自由铰可以限制连接车辆间的横向位移[5]。
在五模块多铰接型有轨电车重量计算中,将由固定铰和弹性铰连接的Mc1车、F1车和Tp车组合为A节车,由固定铰和弹性铰连接的Mc2车和F2车组合为B节车,且均视为刚体。

图3 五模块有轨电车转向架结构图

图4 五模块有轨电车弹簧加垫调整车轮载荷分析模型
图中,L1、L2、L3分别为第1、2、3转向架到J点的距离。
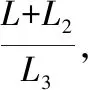
3 有轨电车轮重调整模型
通过弹簧加垫调整轮重是一个典型的准静态分析领域问题。
3.1 弹簧加垫调整车轮载荷的模型
图5所示为有轨电车弹簧加垫调整车轮载荷分析的模型,共有6个自由度:转向架垂向位移X1,点头角α1,侧滚角θ1;车体垂向位移X2,点头角α2,侧滚角θ2。
转向架轴距为2b;二系弹簧纵向距离为2c;轮对左右滚动圆距离为2s;一系弹簧左右间距为2a;二系弹簧左右间距为2d。

图5 有轨电车弹簧加垫调整车轮载荷分析模型
3.2 调整车轮载荷的系统刚度矩阵
系统的刚度关联矩阵元素如表1所示。系统由总共6个自由度和8个弹簧组成,表1有6列,分别代表系统的6个自由度,8行代表8个弹簧刚度元件(为使计算过程简洁易查,本文将一系弹簧进行了等效处理)。
依次给每个自由度1个单元位移,其他自由度位移为0。求得位移在弹簧上造成的变形,填入相应的空格中,即可获得刚度关联矩阵的元素。
假设转向架和车体的形心与重心重合,则转向架和车体分别绕各自形心运动。
定义垂向位移向下为正方向;点头角、侧滚角顺时针为正方向;弹簧元件受压缩为正。
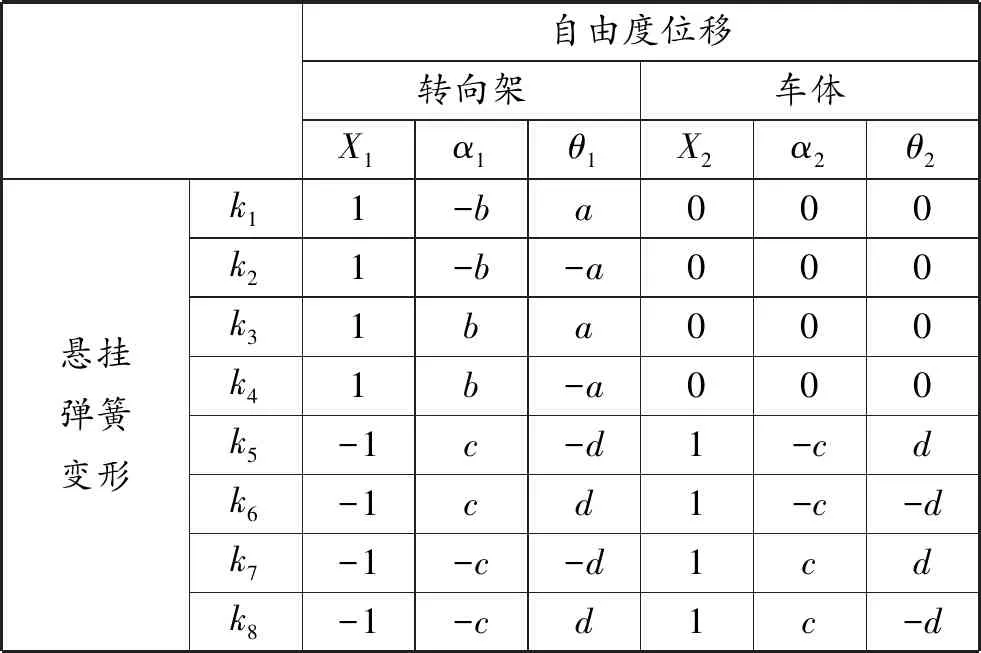
表1 有轨电车弹簧加垫的系统刚度关联矩阵元素
由表1可得系统的刚度关联矩阵为:
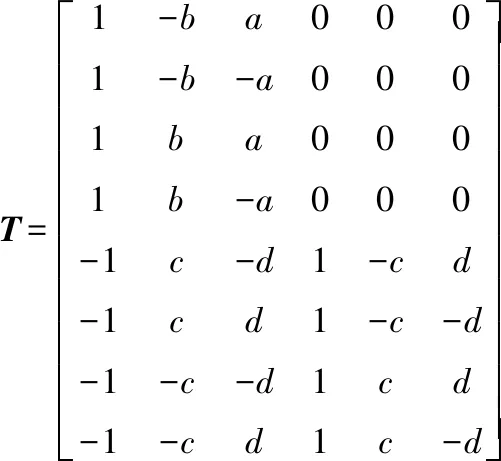
系统的刚度系数矩阵矩阵为:

式中:kp为一系悬挂刚度,ks为二系悬挂刚度。
系统的刚度矩阵为:K=TTkT
3.3 弹簧加垫形成的外力矢量
假设在各弹簧处加垫的厚度为δi(i=1,…,8),则可得加垫矢量:
同理:F0=-TTkδ
3.4 弹簧加垫的系统方程求解
同理可得弹簧载荷变化为:Fs=k(Tx+δ)
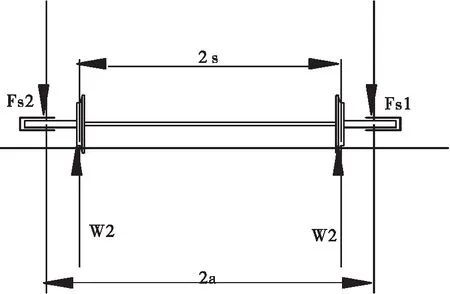
图6 第1根轴受力情况分析图
由图6(以第一轮对为例)可求得各轮对车轮载荷变化:
弹簧加垫后的车轮载荷为:GWi=GWi0+Wi(i=1,2,3,4)
式中:GWi为第i个车轮的载荷;GWi0为第i个车轮的初始载荷。
4 结语
本文针对五模块浮车型有轨电车建立了轮重调整数学模型,通过此模型可以计算在某处弹簧加某厚度垫片对各轮重的影响,为使用计算机程序计算指导轮重调整工作奠定了基础。后续建议进一步研究垫片增加位置与数量对轮重的影响规律,搭建软件计算平台,提高试验效率,节约试验时间。

