改进小波阈值和全变分图像去噪
王永飞
(铜陵职业技术学院信息工程系,安徽铜陵244061)
图像在产生和传送过程中,被噪声污染,质量降低,影响图像的实际应用价值,因此去噪是图像复原中的重要课题,特别在医学、航拍图像和视角系统等领域更显迫切[1]. 许多学者提出了各种修复算法,杜闪闪等[2]提出了整体变分法及其改进算法,该方法可以处理噪声,但边界清晰度不够;冯象初等[3]提出了三维块匹配滤波改进法,但图像平滑度不理想;杨蕴等[4]采用多结构形态学方法虽能去噪,但图像色彩细节不清晰;代晓婷等[5]提出结构联合字典去噪法,该方法可去噪,但图像模糊,运算量大;邓正林[6]提出了卷积神经网络去噪法,该算法梯度弥散不容忽视,需要以资源换效果;高绍雷等[7]用高斯核函数处理图像,修复结果有暗迹. 本文探索一种新的图像去噪算法,克服上述算法中的不足之处,实现图像去噪,提高图像实际价值.
1 算法思想
图像噪声主要包括加性噪声和乘性噪声,加性噪声一般由于仪器自身或相互影响产生,主要有高斯噪声、泊松噪声和椒盐噪声等;乘性噪声主要是指通信信道噪声,可近似认为是加性噪声[8]. 若设Ω是图像的定义域,噪声图像模型可认为是:
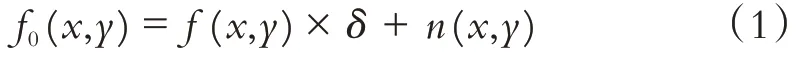
其中:f0(x,y)为含噪图像,f(x,y)为原始图像,δ为乘性噪声,n(x,y)为加性噪声.
图像的像素点信息、纹理信息、结构信息、灰度信息、颜色信息等是图像的主要特征信息[9]. 本文图像去噪修复算法思想从5个维度考虑图像去噪:
(1)分析图像的纹理特征和结构信息,引入小波变换,改进小波阈值函数和阈值提取方式,利用小波分解系数在图像噪声在不同频带上分布强度不同,结合各层噪声小波系数中值绝对变差和数值差,精准估算滤波阈值,清除各频带上噪声小波,实现图像初次去噪,图像去噪后,图像的梯度幅值产生变化,为全变分精确去噪提供基础.
(2)分析图像灰度信息和颜色信息,引入全变分去噪,增加定义加权函数,修改图像灰度梯度幅值公式和图像局部色彩方差公式,实现图像二次精准去噪.
(3)分析图像像素点之间的相关性,引入Laplace算子,提高图像清晰度,提升图像的实用价值.
1.1 改进小波变换实现图像初次去噪
1.1.1 小波变换去噪算法
小波变换通过选择不同的母函数,能获取图像不同时间的信号频率,对图像进行尺度分析,在各尺度上从粗及精分析图像中大量的细节信息.
图像去噪的实质就是找到最接近f(x,y)的估计值. 设ψ(t)为小波变换母函数,对任意函数f(t)∈L2(R),连续小波变换定义为:
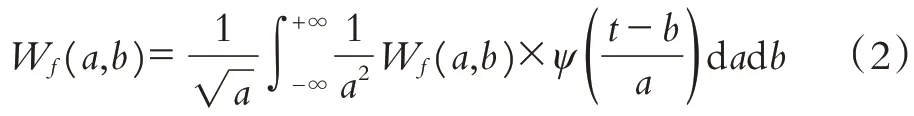
小波重构函数可定义为:
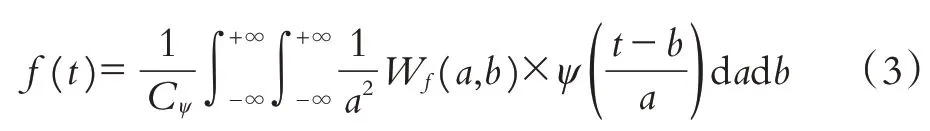
传统的小波去噪方式是通过阈值函数选取阈值,利用该阈值对每层小波系统去噪,常用的硬阈值函数和软阈值函数分别如下:
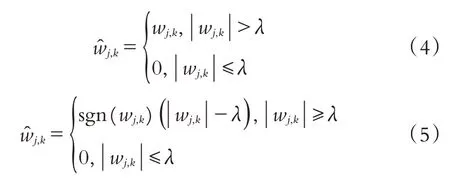
其中:wj,k为噪声图像第j尺度下的第k组小波系数,sgn(·)符号函数,w^j,k是近似估计小波系数,λ是各算法函数中的阈值[11].
阈值λ的选取采用统一阈值法,取值公式为:

其中:σ是噪声标准差,N是图像大小[10].
1.1.2 小波阈值函数和小波阈值选取改进
硬阈值去噪因噪声小波系数直接清零,容易产生伪吉布斯现象;软阈值去噪时,估计值与实际值之间存在一定偏差,影响图像重构效果;另外,还有如折中阈值去噪等方法,图像中都容易出现断点,平滑度不够. 其根本原因是阈值函数选择和阈值选取的问题,因此,为了更好地实现图像去噪,对小波阈值函数和阈值选取方式分别改进如下:
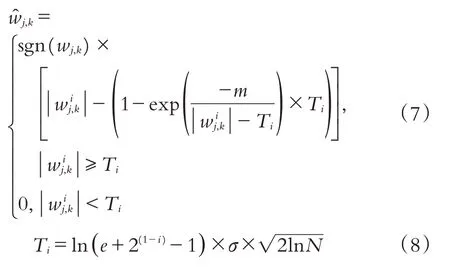
其中:Ti是第i层阈值,m是调节阈值函数的常量.
通过小波变换对图像添加均值为0、方差为0.01的高斯噪声,利用改进的小波阈值函数公式和小波阈值选取公式去噪,选取原始图像和不同方法去噪后图像第5列数据比对,如图1所示.
从图像上看,本文方法去噪后图中的波形最接近原图的波形,虽然改进了算法,图像中仍存在少量噪声,图像信噪比仅为32.69 dB,结构相似度为0.59,但这两项指标比其它方法都高.从波形图像上看,少量有效数据也被清除,图像灰度变化加大,根本原因是阈值选取只能高度近似估计. 这为全变分图像去噪提供了更好的基础.
1.2 引入并改进全变分去噪提升图像去噪效果
1.2.1 引入并改进全变分去噪
全变分图像去噪中关键项是梯度,梯度方向是某像素点灰度变化最快的方向,梯度幅值大小由该区域像素点灰度变化大小决定,通过小波去噪,改变了图像中灰度变化,防止了图像出现阶梯效应.
f整体变分定义为:
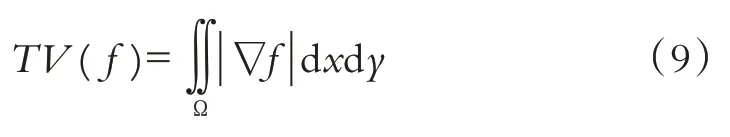
图像噪声加大了图像梯度变化,基于全变分去噪可认为是极小化问题:
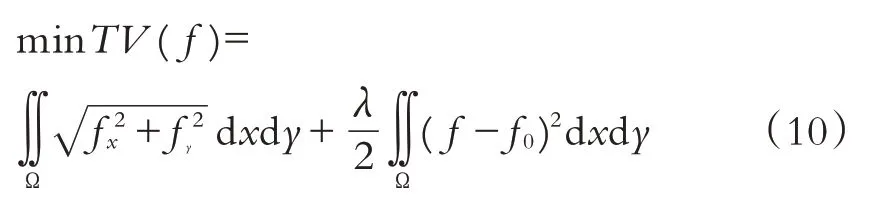
式中:λ为常数,保持原图像特征,表达图像边缘.
相应的Euler-Lagrange可定义为:

为改进图像去噪效果,以更好地修复噪声,利用中心差分计算梯度:
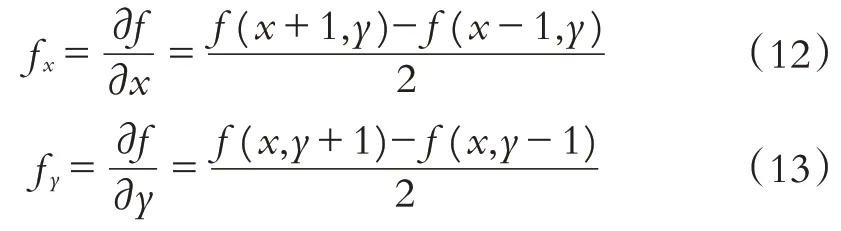
其中fx和fy分别是中心差分的水平方向梯度和垂直方向梯度.
第n次迭代时,梯度幅值为:
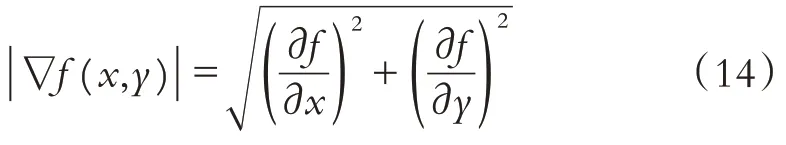
图像局部方差表达图像细节信息,第n次迭代时,以像素点(x,y)为中心的3×3区域局部方差可定义为:
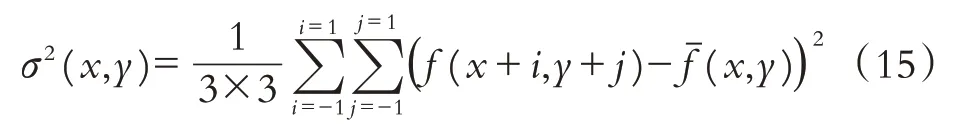
其中:σ2(x,y)为局部方差,fˉ(x,y)为该区域均值.
为了更好地保护图像边缘信息,增加定义加权函数如下:
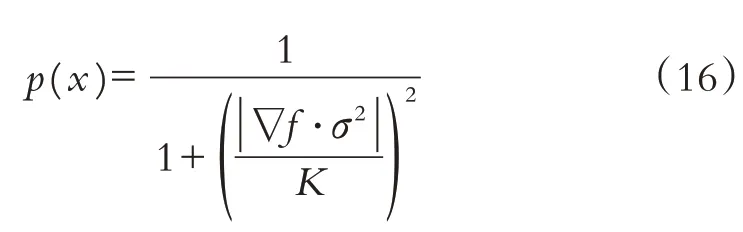
其中K为常数.
利用改进后的全变分去噪,对小波去噪后的图像进行去噪,结果如图2所示.

图2 全变分图像去噪Fig.2 Total variation image denoising
从图像上看,全变分图像去噪后图像质量得到大幅提升,图像的信噪比达到33.48 dB,图像相似度达到0.66,信噪比提高了0.79 dB,结构相似度提高了0.08. 但去噪后的图像分辨率降低,图像清晰度不够.
1.2.2 引入Laplace算子提高图像清晰度
Laplace 算子具有旋转不变性的特征,图像加噪后,图像灰度发生很大的突变,选取突变点p的3×3邻域,图像利用小波变换,提取图像去噪阈值,p区域的绝对数值差值超过此阈值,形成过零点. 对图像x和y方向二阶导数差分,获得Laplace 算子x和y方向的离散函数:
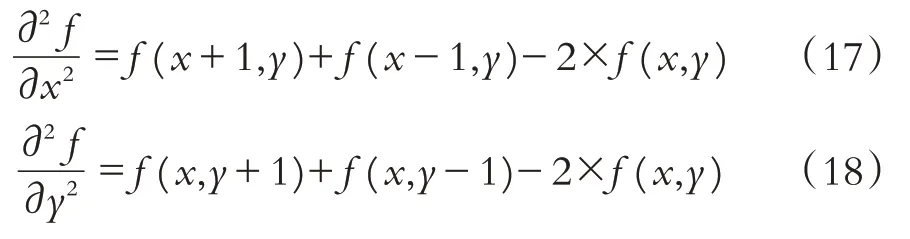
Laplace算子差分形式为:
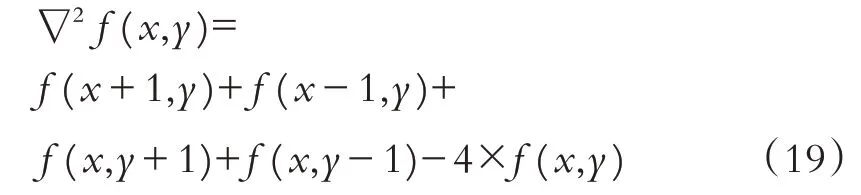
使用Laplace 算子卷积扫描噪声图像,与重合的像素相乘求和后回赋,对图像首尾行列像素直接赋值为0. 若背景特征不明显时,利用Laplace 算子操作后的像素恢复图像,公式为:
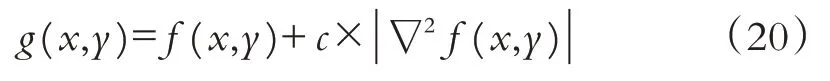
其中,Laplace 算子卷积中心系数为正时c=1,否则c=-1;g(x,y)为卷积后图像.
利用Laplace 算子,对全变分去噪后的图像再处理,结果如图3所示.

图3 图像分辨率提升Fig.3 Image resolution enhancement
从图像上看,引入Laplace 算子后,图像清晰度改善明显,图像的信噪比提高了12.35 dB,结构相似度提高了0.01,图像的实用价值得到大幅提升.
2 算法通用性分析与验证
实验的运行平台为32 位Windows 7 旗舰版和MATLAB 2012b,图 片boat.jpg 大 小 为500 px ×281 px. 对所采用的图像均添加均值为0、方差为0.01 的高斯噪声,利用本文算法与其它当前主流算法对结构和纹理信息都很丰富的图像boat.jpg 进行对照分析,如图4所示.
从视觉角度看,文献[8]图像中噪声减弱;文献[10]图像中噪声明显;文献[12]图像中有点模糊,且仍有噪声;文献[13]图像中颜色变化不连续,且仍有噪声暗影;文献[3]船头出现块状填充;本文算法修复效果最优.
从图像信噪比和结构相似度两方面分析,结果如表1所示.
由表1 可知,本文算法去噪后的图像结构相似度最高,信噪比最大,文献[12]的图像结构相似度较高,但信噪比较低. 综合考虑,本文图像去噪算法更具有实用性.
为验证本文算法对任何图像去噪效果,即验证本文算法的通用性,再次对另一图像house.png(大小为512 px×410 px)进行实验分析,如图5所示.
在此增加了文献[4]的修复图,但修复效果很不理想;文献[8]和文献[10]图像都有噪声;文献[12]图像有点模糊,且仍有噪声;文献[13]图像仍有噪声;文献[3]屋顶过于平滑,且屋顶边缘出现锯齿. 可见本文算法修复效果最优.
从图像信噪比和结构相似度两方面分析,得到如表2所示的结果.由于文献[4]图像效果差,图像信噪比和结构相似度在表中未予列出.

图4 本文算法与其它5种算法去噪效果比较Fig.4 The denoising effect of this algorithm was compared with other 5 algorithms
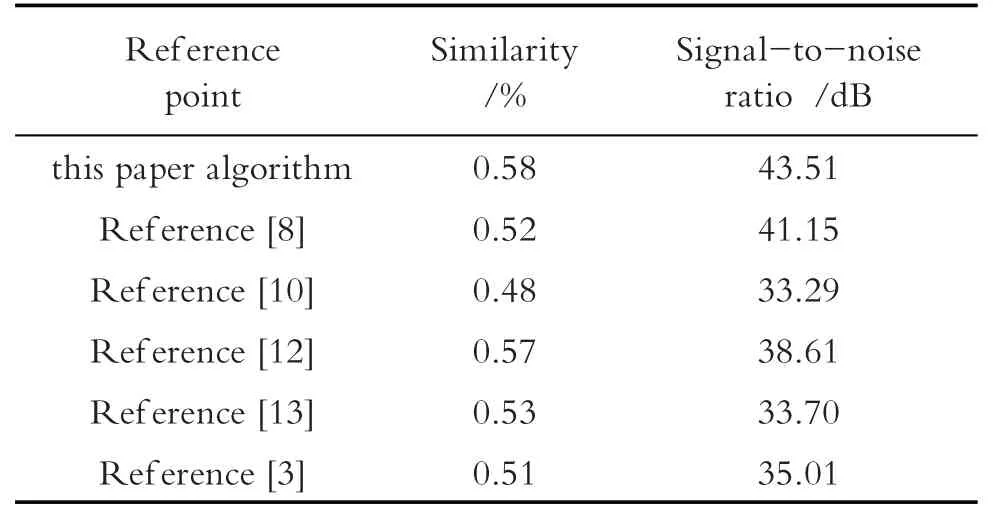
表1 去噪后图像与原图像数据比较(boat.jpg)Table 1 Data comparison between de-noised image and original image(boat.jpg)
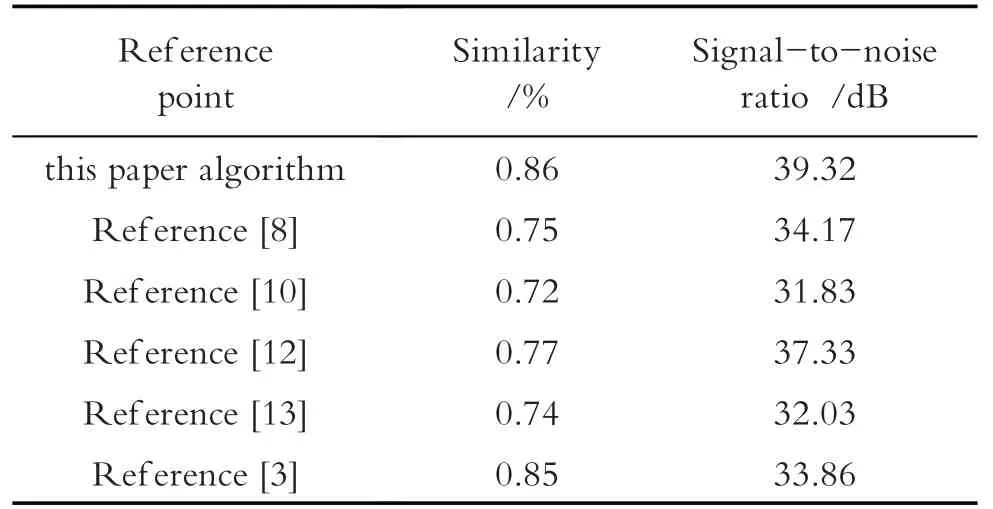
表2 去噪后图像与原图像数据比较(house.png)Table 2 Data comparison between de-noised image and original image(house.png)

图5 本文算法与其它6种算法去噪效果比较Fig.5 The denoising effect of this algorithm was compared with other 6 algorithms
从表2 的数据可知,本文所列算法去噪后图像信噪比和结构相似度都很高,但本文算法修复后图像信噪比较文献[13]高出7.29 dB,说明本文算法通用性更好.
3 结论
本文设计了一种图像去噪的算法,通过引入改进的小波变换去噪,初步清除图像噪声,去噪的同时也扩大了图像的梯度幅值变换,为全变分图像去噪提供了基础,改进了全变分图像去噪,增加了保护图像边缘信息的加权函数,提高了图像修复效果,引入Laplace 算子后,提高了图像清晰度. 从视觉效果、图像信噪比和结构相似度三个方面与当前主流算法图像修复效果进行比较,证明了本文图像去噪算法的有效性、实用性和通用性.

