利用测量机器人进行联系测量的方法与精度分析

刘少春

（河北能源职业技术学院矿产资源与建工系，河北唐山063000）

联系测量技术应用范围广，城市轨道交通工程、隧道工程、地下采矿工程都需要利用该技术建立井上下统一的测量系统，保证地下工程按设计施工，确保贯通。传统方法是通过矿井定向和高程传递两种方式实现，为了解决传统方法投点、连接测量、高程传递分开进行，对测量条件要求较高且测量误差较大的问题，需要利用先进的测量技术和手段，开展自动化、高效率的联系测量方法研究。本研究在利用全站仪、光学铅垂仪、陀螺经纬仪进行一体化联系测量成果［1-4］的基础上，提出采用测量机器人与陀螺全站仪联合进行联系测量的方法。分析了利用测量机器人测三角高程代替水准测量进行高程传递，以及利用测量机器测导线和陀螺全站仪进行定向的精度。针对井上下连接测量时井下测量机器人寻找上部棱镜困难的问题，研制了连接专用工具，解决了黑暗环境下测量机器人自动搜索棱镜困难的问题，并结合工程实例进行了方法可行性验证，可为井下测量系统建立提供可靠的技术支撑。

1 测量机器人与陀螺全站仪联合进行联系测量技术

1.1 连接测量

如图1所示，在井盖传递孔O上安置专用上下连接装置，在井上定向连接点D上安置测量机器人，后视C点，前视O点，城市轨道交通工程按测角中误差±2.5″，即四等导线的导线要求，隧道及矿山工程按±5″导线要求测出棱镜中心坐标［5-8］。

井下利用参照物在图1中O′点处安置测量机器人，后视O点下棱镜，前视在井底车场稳固的岩石中或碹体中埋设的永久导线点C′上所安置的棱镜，同样城市轨道交通工程按测角中误差±2.5″，即四等导线的导线要求，隧道及矿山工程按±5″导线要求测角、测距、测高差、量取视高，测完后在O′点处安置棱镜作为后视，在C′点上安置陀螺全站仪，前视D′点测水平角、距离，对边C′D′进行陀螺定向，定向程序为2-2-2。

井下定向边C′D′的坐标方位角为

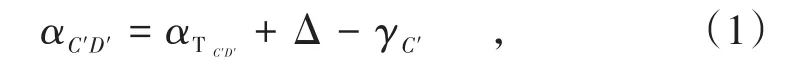
式中，α为坐标方位角；αT为陀螺方位角；Δ为仪器常数；γ为子午线收敛角。

根据井下连接测量测出的水平角βC′、βO′以及距离DC′O′、DO′O、陀螺定向求出的αC′D′，按式（2）计算边C′O′与边O′O的方位角αC′O′、αO′O：

井下起始点C′点坐标(XC′,YC′,HC′)可进行如下计算：

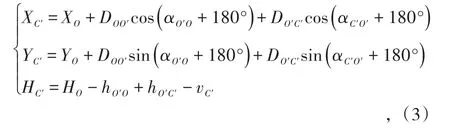
式中，XO,YO,HO为O点坐标，m；DOO′为O点与O′点的水平距离，m；DO′C′为O′点与C′点的水平距离，m；αO′O、αC′O′为坐标方位角；hO′O为O′点与O点高差，m；hC′O′为C′点与O′点高差，m；vC′为仪器高，m；

1.2 误差分析

1.2.1 利用测量机器人测三角高程代替水准测量的误差分析

利用测量机器人进行三角高程测量时，垂直角水平距离对观测高差的影响可进行如下分析［2-3］。井上部分有下式成立：

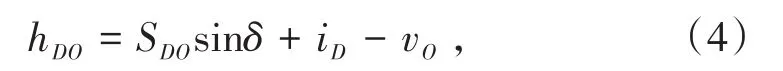
式中，hDO为D点和O点的高差，m；SDO为D点仪器中心和O点棱镜中心的斜距，m；δ为垂直角；iD为D点的仪器高，m；vO为O点棱镜至连接装置底部棱镜中心高度，m。

根据误差传播率有：

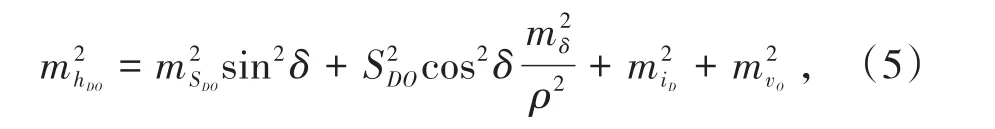
式中，mhDO、msDO、mδ、miD、mvO为对应量的中误差。

井下部分有下式成立：

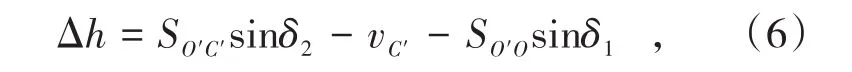
式中，Δh为O点处底部棱镜中心和C′点的高差，m；SO′C′为O′点仪器中心和C′点棱镜中心的斜距，m；δ2为O′点仪器中心和C′点棱镜中心的垂直角；SO′O为O′点仪器中心和O点处连接装置底部棱镜中心的斜距，m；δ1为O′点仪器中心和O点处连接装置底部棱镜中心的垂直角；vC′为C′点至棱镜中心高度，m。

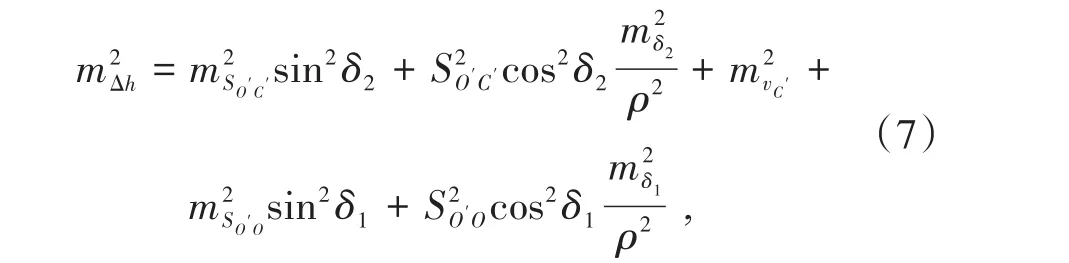
式中，mΔh为 Δh中误差，mm；mSO′C′为的中误差，mm；的中误差，mm；mδ1、mδ2分别为δ1、δ2的中误差，s；mvC′为vC′的中误差，mm。

以目前常用的测量机器人TS60、索佳SX-101T、SX-102T为例，TS60测量机器人具有0.5″测角精度、±(0 .6 mm+1.0 × 10-6⋅S（)S为观测距离，km）测距精度［7，9-10］，并且设置双照相系统，操作简便。索佳 SX-101T具有1″测角精度、SX-102T具有2″测角精度，两种仪器3种测距模式主要技术指标为：①棱镜测距精度为 ±(1 .5 mm+2.0 × 10-6⋅S)；②无棱镜测距精度为±(2 .0 mm+2.0 × 10-6⋅S)；③ 反 射 片 测 距 精 度 为 ±(2.0 mm+2.0 × 10-6⋅S)。

本研究高程和平面点位精度分析中，均以2″测角精度，±(2 .0 mm+2.0 × 10-6⋅S)棱镜测距精度的测量机器人为例进行。在不考虑起始点误差的情况下，仪器高、棱镜高测量误差均设定为1 mm，mδ= ±2″，mS= ±(2 .0 mm+2.0 × 10-6⋅S)，SDO=SO′C′=50 m，δ=2°,δ2=2°

C′点高程中误差mHC′与O′点仪器中心和O点处连接装置底部棱镜中心的垂直角δ1的关系可表示为

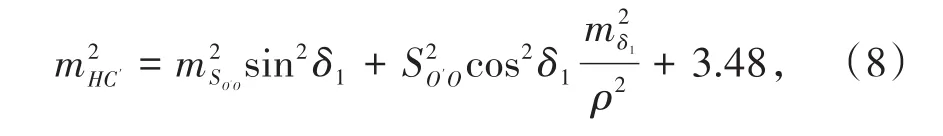
式中，mHC′为C′点高程中误差，mm；δ1为O′点仪器中心和O点连接装置底部棱镜中心的垂直角；mδ1为δ1的测角中误差；SO′O为O′点仪器中心和O点连接装置底部棱镜中心的斜距，m；mSO′O为SO′O的中误差，mm。

以O′点安置测量机器人的仪器中心至O点连接装置底部棱镜中心的水平距离200 mm为例，进行mHC′与矿井深度关系的分析，具体计算结果见表1。

注：DO′O为O′处安置测量机器人的仪器中心至O点处连接装置底部棱镜中心的水平距离，m；VO′O为矿井深度，m；SO′O为O′处安置测量机器人的仪器中心至O点处连接装置底部棱镜中心的倾斜距离，mm；δ1为O′点仪器中心和O点处连接装置底部棱镜中心的垂直角；mHC′为C′点高程中误差，mm。

由表1可知：采用测量机器人进行三角高程测量，可满足矿井联系测量高程传递的精度要求。

1.2.2 利用测量机器人测导线井下起始点的点位误差分析

井下起始点C′的点位误差为［4］

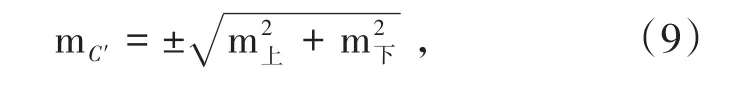
式中，mC′为C′点点位误差，mm；m上为井上测量误差引起的O点处连接装置底部棱镜中心的点位误差，mm；m下为井下测角、测距、定向引起的C′点的点位误差，mm。

设井上下一测回方向观测中误差m=±2″，采用棱镜测距精度为±(2 .0 mm+2.0 × 10-6⋅S)的测量机器人进行导线测量，一测回角值测量中误差mβ=±2.83″，两测回测量中误差为mβ平= ±2″，本研究按mβ= ±2.5″四等导线的精度要求进行计算。井上部分点位测量中误差计算公式为

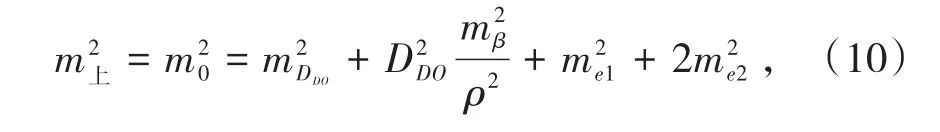
式中，mO为O点的点位误差，mm；DDO为D点仪器中心和O点棱镜中心R的平距，取50 m；mDDO为DDO中误差，mm；me1、me2分别为仪器和前后视棱镜对中误差，取1 mm。经计算，=7.78 mm。

德国GYROMAT2000、GYROMAT 3000型全自动陀螺仪一次定向精度mα可达±3.6″［5］，国产 AGT-1和AFS-1型自动陀螺经纬仪一次定向精度mα在±5″以内，Y/JTG-1tu′p′luo陀螺全站仪一次定向精度mα在±7″以内，NTS-342G型陀螺全站仪一次定向精度mα有±10″和±15″两种。综合分析国内外陀螺全站仪一次定向精度，本研究mα=±10″。那么，井下部分点位测量中误差计算公式为

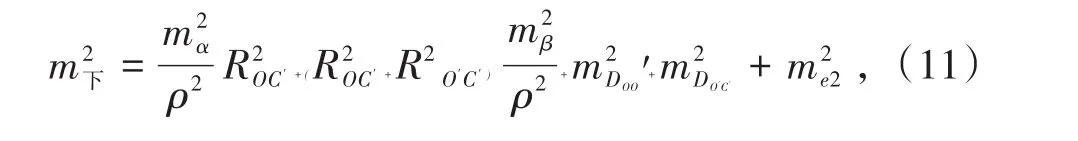
式中，ROC′、RO′C′为C′点与O和O′的连线长度，m；me2为C′处棱镜对中误差，取1 mm；mDOC′、mDO′C′为与OO′和O′C′距离中误差，mm。经计算，=16.07 mm。

于是，C′点位误差为±4.89 mm。可见，利用测量机器人与陀螺仪进行平面联系测量的精度远高于传统方法。

2 井上下连接专用工具的研制及使用方法

2.1 井上下连接专用工具研制

平面联系测量包括投点和连接两部分，高程联系测量有长钢丝、长钢尺、全站仪天顶3种方法。传统的平面和高程联系测量是分开进行的，利用测量机器人与陀螺全站仪联合进行联系测量，导线和三角高程测量同时进行，则无需投点，只需进行井上下的连接测量，因而研制一个连接井上下的专用工具很有必要［11-14］。该连接装置需要重点解决两个问题：首先上下测量机器人瞄准的棱镜同心问题，其次井下测量机器人后视棱镜的照明问题。

本研究研制小型专用工具如图2和图3所示。本研究研制的连接工具上部保留了微型全站仪棱镜三脚架的功能，由棱镜、水准器、可调节三脚架组成，下部在对中杆的下端加工连接一个与上边棱镜同心的棱镜，为解决下部棱镜扣在井盖孔上后发光照明问题［15-17］，在棱镜下部内壁粘贴LED 5 V防水电池盒灯条，并对电池盒和开关位置进行了设计，可有效解决井上下连接测量和井下测量机器人寻找上部棱镜困难的问题。

2.2 微型连接装置使用方法

在井盖上设置一个φ30 mm左右的一个传递孔，将微型连接装置的下部棱镜放置于传递孔上，打开电源开关，张开三脚架整平，上部棱镜对准井上定向连接点上安置的测量机器人，井上下进行导线测量和三角高程测量［7］，井下配合陀螺仪定向，便可将测量系统传递到井下。

3 工程实例

为了建立图古日格金矿井上下统一的测量系统［16］，采用全站仪、陀螺全站仪、钢丝投点、全站仪天顶导入高程和测量机器人与陀螺全站仪联合进行联系测量两种方法进行了对比测试［6］，测试区域为该矿十六号竖井的一水平和二水平［15］。首先，地面在近井网的基础上，导线按5″要求，高程采用三角高程对向观测的方法，测出下放钢丝平面坐标和棱镜中心的三维坐标，实测路线为A4—A10—XK1—XK2—XK3—ZX—钢丝，A4—A10—XK1—XK2—XK3—ZX—O（棱镜中心）；井下一水平实测路线为ⅠSM2—ⅠSM1—钢丝，ⅠSM2—ⅠSM1—O′—O；井下二水平实测路线为ⅡSM2—ⅡSM1—ZD—钢丝，ⅠSM2—ⅠSM1—ZD—O′—O。一水平陀螺定向ⅠSM1—ⅠSM2坐标方位角为 24°06′27″，二水平陀螺定向ⅡSM1—ⅡSM2坐标方位角为24°20′45″。按井上下连接测量的方法进行观测［17］，对观测数据进行整理和计算，求得两种方法的对比计算结果见表2。

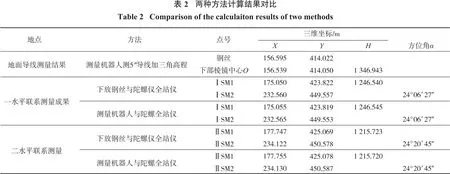
由表2可知：高程传递利用全站仪天顶法和测量机器人三角高程测量的一水平差值为-5 mm，二水平差值为+3 mm，平面坐标采用下放钢丝和陀螺仪全站仪测量机器人与陀螺全站仪两种方法传递，一水平ⅠSM1点差值Δx=-5 mm，Δy=+3 mm；ⅠSM2点差值Δx=-5 mm，Δy=+4 mm。二水平ⅡSM1点差值Δx=-8 mm， Δy=-9 mm； Ⅱ SM2 点 差 值Δx=-8 mm，Δy=-9 mm。可见，两种方法投点误差在规程允许的20 mm以内，说明本研究采用测量机器人与陀螺全站仪联合进行联系测量的方法可行，精度可靠，简单方便。

4 结论

（1）采 用 测 角 精 度 2″、测 距 精 度 ±(2.0 mm+2.0 × 10-6⋅S)的测量机器人进行三角高程测量，能够满足城市轨道交通、隧道、地下采矿等工程高程传递的精度要求。

（2）利用2″及以上测量机器人，按四等要求施测导线，陀螺全站仪一次定向精度10″进行平面联系测量，井下起始点平面点位误差可控制在10 mm以内，精度优于传统方法。

（3）小型连接专用工具的研制，可有效解决上下连接测量棱镜同心和井下测量机器人寻找上部棱镜困难的问题，具有推广价值。采用测量机器人与陀螺全站仪联合进行联系测量，精度可靠，简单方便，具有可行性。