爆堆前冲和后冲距离的GSM/GA-SVM预测模型

何晓华

（中钢集团马鞍山矿山研究总院股份有限公司，安徽马鞍山243000）

爆破作业作为最主要的破岩方式之一，目前被广泛应用于水利、矿山、隧道等领域［1-3］，其成本低，见效快，但是爆破作业有时不可避免地会对周围的环境和工作人员产生不良的影响，比如爆破振动、飞石、噪音、粉尘［4］等，这些不良的影响轻则带来经济损失，严重的话则会引发经济纠纷或者导致人员伤亡，从而影响矿山的正常作业。究其原因，主要是影响爆破效果的因素过于复杂，这些影响因素相互影响，与爆破效应之间构成了一个复杂的关系，难以用一个函数来概括所有的影响因素；为了避免或者减轻这些危害的产生，各个国家都制定不同的爆破安全判据，比如德国、英国、美国等，我国也制定了《GB 6722—2014爆破安全规程》，与此同时，众多学者考虑采用数值模拟，经验判定，或者数值计算的方式对爆破效应进行分析，所产生的结果对减轻爆破危害带来了很大的益处。

然而，目前对于爆堆的研究主要还是集中对爆堆形态和爆破岩石质量的研究上［5-6］，对于爆堆位移的研究目前在爆破领域仍然有待于进行深入挖掘和分析。爆堆位移主要可以分为爆堆前冲位移和爆堆后冲位移，爆破前冲位移是指岩石被爆破气体推动从而整体产生向前位移的现象；爆堆后冲位移是指爆破作业后矿岩在工作面后方的冲击力作用下，爆堆整体向后位移的现象。传统的露天矿爆堆位移分布测定主要是采用摄影法，然后借助图像分析的技术对成果进行鉴定，但是这种技术往往需要耗费大量的时间，鉴定结果也受摄影技术的影响。本研究考虑将先进的监督式学习技术应用到爆堆位移的预测和分析上，目前比较流行的监督式学习方法有支持向量机、随机森林、神经网络等。支持向量机（SVM）［7］作为机器学习领域中非常重要的一种算法，最开始由Vapnik等人提出，同其他机器学习算法一样，其衍生于统计学习理论。支持向量机方法更擅长处理小样本和高维度的问题，因此，一经提出便得到了广泛的应用，能够很好地处理非线性映射问题。支持向量机可以用来处理分类和回归问题，其涉及到的超参数较少，主要是C值和g值，因此，借助启发式算法对支持向量机的超参数进行优化，无需耗费太多的时间，也不易产生局部极值问题。考虑到本研究所要分析的爆堆位移预测模型涉及到的影响参数较多，而且可用的数据集较少，因此作者考虑将网格搜索方法（GSM）和遗传算法（GA）［8-11］与支持向量机模型相结合，建立了基于GSM/GA-SVM的爆破前冲和后冲距离预测模型。

1 计算原理简述

1.1 基于GA的SVM参数优化

在SVM算法中，可以利用核函数向高维空间映射并解决非线性的分类问题，但是核函数参数和惩罚因子C值对相应预测的精度有很大的影响。当C值变化时，模型的容错能力变小，泛化能力也随之减小，当调高相关参数时，其精度有所增加但容易出现过拟合的问题。传统的方法中人为因素比重较大，主观性较强。遗传算法（GA）是模仿自然界中生物进化机制（优胜劣汰和遗传变异）来搜索样本空间最优解的优化方法。GA算法设置相应的适应度函数并对运算后子代进行相应的优化，使其收敛并得到最优解。

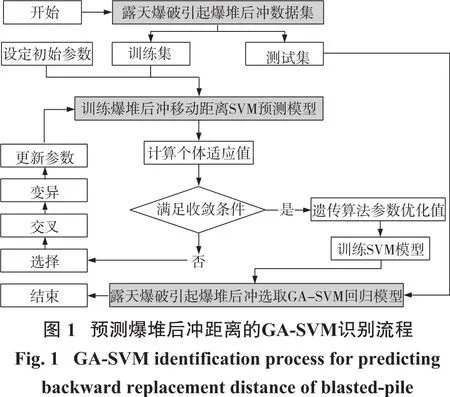
根据GA的相关特性［8］，将其与SVM结合起来并对算法中的参数进行优化，具体步骤如下：

（1）收集露天爆破引起后冲数据并进行相应预处理，进行归一化处理来避免各部分数值相差太大而造成偏差，将样本数据分为训练样本和测试样本，训练SVM后冲模型，计算相应的交叉概率。

（2）设置惩罚因子C和不敏感参数g的阈值，用一定方式进行编码，构建合适数量的种群并对其进行初始化。

（3）构建适应度函数判断个体的适应情况，计算适应值。若满足相应的条件，则进行解码获得最优的参数C和g，将获得的参数输入到SVM中收集相应的误差。

（4）根据适应值和阈值来剔除适应性较差的个体，采用轮盘赌法算子，确保选中适合的样本。

（5）将群体内部的个体根据交叉概率来进行部分的交叉，并用变异概率来改变样本中的一些特征，随机选择变异的个体。

（6）判断新一代的群体是否满足收敛条件，若满足则结束相应的迭代并用相关的GA-SVM算法来解决露天爆破爆堆后冲问题，其计算流程图如图1。不符合条件则返回继续更新参数并进行计算。

1.2 基于网格搜索的SVM参数优化

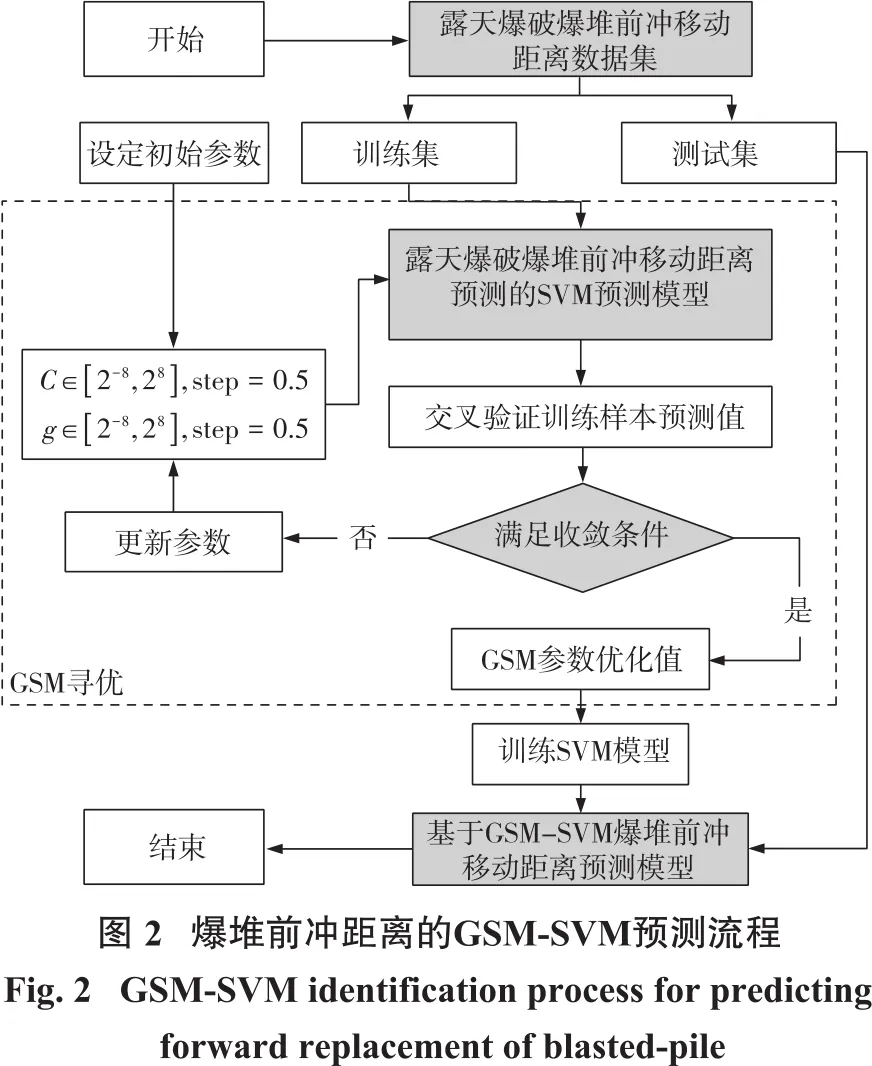
SVM中将样本数据由现有空间向更高维度转化过程中，涉及到相关参数的优化方法有很多。常见的有人工试算、粒子群优化和遗传算法等方式。人工试算过程中不确定性因素较多，同时主观性比重较大，因个体差异而产生变化；遗传算法模块较为灵活，使得算法实现过程中代码较为复杂且难以实现。同时时间复杂度较为明显，计算过程会耗费较长的时间；粒子群优化算法在寻求最优解过程中收敛过早，并且寻找局部最优解的能力较差。网格搜索法空间复杂度较为明显，但是其搜索到的可能组合较为全面。先设置大步长进行粗略搜索，获得目标的大致范围并根据设置的小步长来进行精确搜索，具体步骤如下：

（1）采用网格搜索方法来建立SVM的惩罚因子C、参数g值和相应的搜索步距。其中C和g的范围都为2-8～28，其值太小时会影响模型的学习能力，步长都设定为0.5，建立起一个C-g坐标系。

（2）采用科学的方法实地收集数据并进行相应的处理。将爆堆数据根据实际需要进行均匀分组，任意挑选其中一组作测试之用，其他数据用来训练模型。根据C-g坐标系随机选择一个参数来进行训练并用测试数据来验证，计算错误率。

（3）运用建立的GSM-SVM模型来对所有收集的样本来进行交叉验证训练预测值。

（4）判断预测值是否满足收敛条件，若不满足则更新参数继续计算，若满足则记录相应优化值，用等高线绘出各组C、g值相对应的预测准确率，进而获得最优C、g值。

（5）用露天爆破爆堆前冲测试数据验证优化的GSM-SVM预测模型计算流程图如图2所示［10］。

2 模型建立与分析

2.1 确定爆堆前冲和后冲距离输入/输出参量

在露天采矿中，往往采用爆破的方式进行矿石的开采工作，爆破作业虽然高效但是由于爆破效果受众多因素影响，因此爆破作业可能会产生一些不良的影响，比如会引起爆堆前冲和后冲，前冲会导致爆堆沿抵抗线方向抛出一定距离，当这一距离过大时，可能会导致部分矿石移动到临近的台阶上，从而影响运输工作，并且可能会对工作人员带来危险；爆破后冲则会引起爆破威力沿着抵抗线相反的方向进行传播，从而会降低周围岩石的稳定性。因此必须控制好爆堆的前冲距离和后冲距离。为准确预测爆堆前冲距离和后冲距离，本次实验选择第1排的炮孔的孔深、孔距、抵抗线距离、坡角、超深长度、药量、炮孔堵塞长度，以及第2～8排炮孔的孔深、孔距、排距、超深长度、药量、炮孔堵塞长度作为影响因素，以爆堆的前冲距离和后冲距离作为因变量，分别建立了爆破前冲和后冲距离预测模型。

为了验证本研究提出的爆破前冲和后冲移动距离预测优化SVM模型的有效性和实用性，在现场进行了大量的爆破实验，并实录了40组爆破前冲和后冲移动距离实测数据（表1）作为SVM预测模型的学习训练样本和测试样本，根据预测模型的需要，对于爆破前冲预测模型，将数据集按照8∶2的比例划分为训练集和测试集；对于爆破后冲预测模型，将数据集按照7∶3的比例划分为训练集和测试集。有时收集到的数据量纲不同或是二者数值相差较大但对目标对象影响程度相同，因此需要对收集到的现场数据进行归一化处理，使其能够在同一运算环境中进行计算。令Lv、Sv分别为样本中变量的最大值、最小值，则任意样本变量h可规范化为

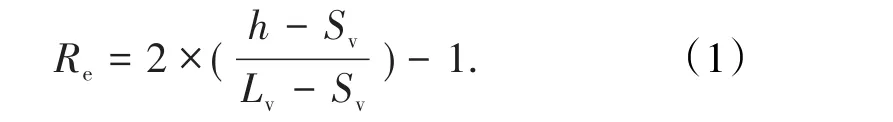
通过式（1）的归一化处理之后，各种类型的现场数据都能够被转换并限制在区间［-1，1］之间的常量，该步骤使得数据能够被直接输入到模型中并进行相关运算。

在数据处理中，经常会遇到特征维度较多甚至特征维度比样本数量多得多的情况，若直接将所有的影响变量用于构建预测模型，则会产生不良的影响：一是因为冗余的特征会带来一些噪音，影响计算的结果；二是因为无关的特征会加大计算量，耗费时间和资源。因此在构建预测模型之前，采用PCA降维的技术，PCA降维技术是指降低空间复杂度的情况下最大限度地反映目标本身的特性。理论上讲，对目标搜集的信息越多意味着了解越全面，但是随着样本维度增加可能会使计算量呈指数增长。为了平衡时间复杂度和预测准确性之间的关系，需要我们尽可能提取少的但又能代表目标本质特征的参数，同时在高维向低维的跃迁过程中尽可能减少数据信息的损失，从而提高整个模型的预测准确性。在本次建模过程中，通过PCA降维技术，将输入因子由13个下降到6个，从而去除了干扰特征，并节省了计算时间。

2.2 爆堆前冲距离预测的GA-SVM预测模型

注：孔深、孔距、抵抗线、超钻、堵塞长度、前冲距离、后冲距离的单位为m，坡角的单位为（°），药量的单位为kg/m³；本次试验孔径取120 mm；台阶高度8～10 m；装药结构为耦合连续装药。

确定爆堆前冲移动距离时，SVM模型输入向量为第1排的炮孔的孔深、孔距、抵抗线距离、坡角、超钻长度、药量、炮孔堵塞长度，以及第2～8排炮孔的孔深、孔距、排距、超钻长度、药量、炮孔堵塞长度，模型输出为爆堆前冲移动距离，在收集的参数和输出之间由模型建立对应的函数关系。在现场收集到的40组数据基础上随机挑选8组用作测试数据之用，其余的32组数据用于训练模型。在SVM模型中，一定范围内的C值能提高模型的预测性能，但是其过高会使得回归效果变差。不敏感参数g用于描述相关曲线的拟合程度，其泛化能力与g值成反比。SVM采用高斯核函数将样本由低维空间向高维空间的转换，同时根据GA算法找出C和g的各种组合并根据相应函数寻求最优组合，寻优的迭代过程如图3所示。GASVM组合模型的算法过程代码由Matlab实现，在LibSVM工具箱的基础上进行交叉验证，最终获取组合模型最优情况下的C、g值。交叉验证系数为5，GA算法中相应参数取值如下：样本大小为20，极限迭代次数为100。其中，C和g的调整范围是：C∈［0，102］，g∈［0，102］，分别得到训练集和测试集的真实值与预测值的对比，如图4、图5所示。最后，采用平方相关系数R2和均方误差MSE 2个指标来衡量组合模型的性能。

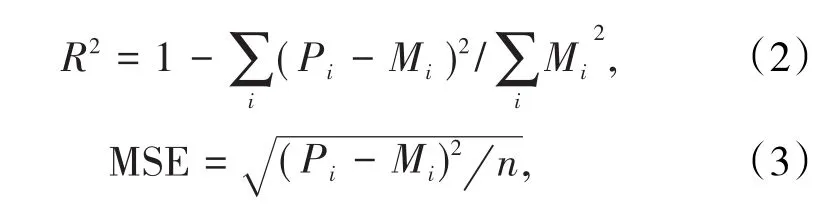
式中，Mi，Pi表示实测值和预测值；n表示输入数据对的数量。

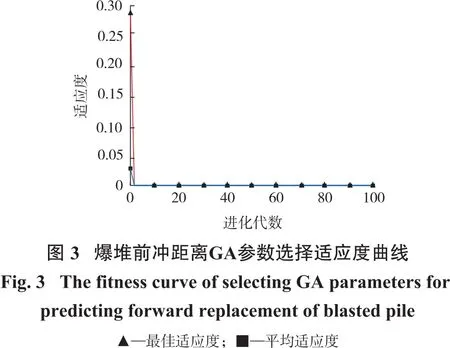
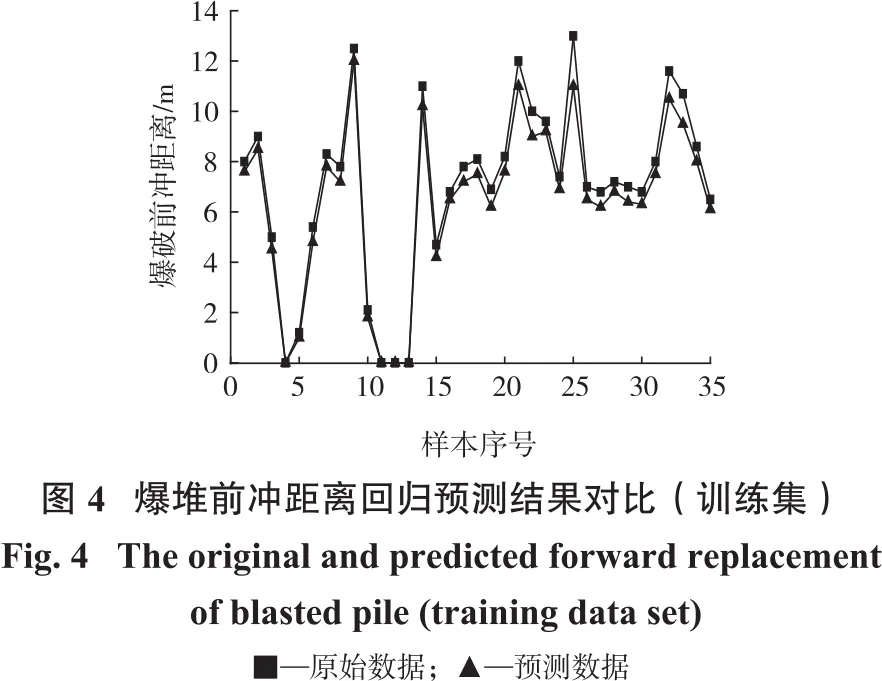
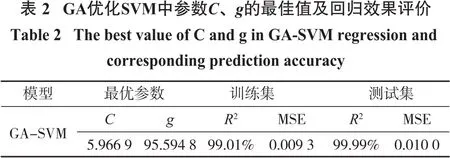
由图3得出，子代代数增加使得相关函数的适应度接近于一个定值，在这个过程中GA算法的作用得到体现。在进化1代左右后，最佳适应度值收敛，通过计算，当爆堆前冲距离回归预测模型的SVM超参数为C=5.966 9，g=95.594 8时，对应的训练样本R2为99.01%，测试样本R2=99.99%；详见表2。根据表2和图4、图5中的信息可知，GA-SVM组合模型的预测曲线与实际情况对比可知其贴合度较高，且二者误差在一个可以接受的范围内。因此，用该组合模型适用性较强，在爆堆前冲预测方面性能优越。

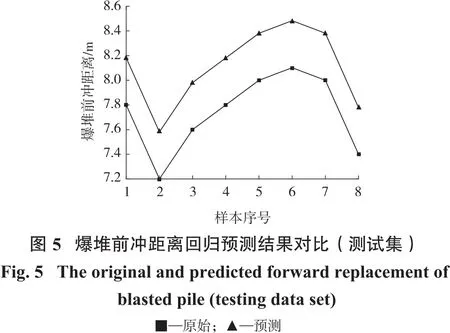
由上述预测结果可知GA-SVM组合模型具有能够使SVM算法模型适用范围更加广泛，对数据分析更全面的优点。将结构风险降到最低和泛化能力作为SVM的突出特性，二者有机结合起来能够弥补单个GA算法难以进行系统调控的缺点，同时获得多个局部最优解并且筛选出整体最优值。SVM算法中凸函数优化求解问题能够避免筛选的目标值过于片面化，确保得到的是全局最优解，同时有利于降低向量的维度。在爆堆前冲预测问题中，GA-SVM与真实结果较为接近。该组合模型在原有模型适用范围基础上，进一步增强其数据整合分析的能力。在现场遇到的此类问题中，可根据实际选取具有代表性的数据进行分析预测。

2.3 爆堆后冲距离预测的GSM-SVM预测模型

同理，确定爆堆后冲距离时，SVM模型输入向量为第1排的炮孔的孔深、孔距、抵抗线距离、坡角、超钻长度、药量、炮孔堵塞长度，以及第2～8排炮孔的孔深、孔距、排距、超钻长度、药量、炮孔堵塞长度，模型输出为爆堆后冲移动距离，并根据此建立映射，选取收集的40组爆堆后冲移动样本中28组为训练样本，余下12组作为测试样本。

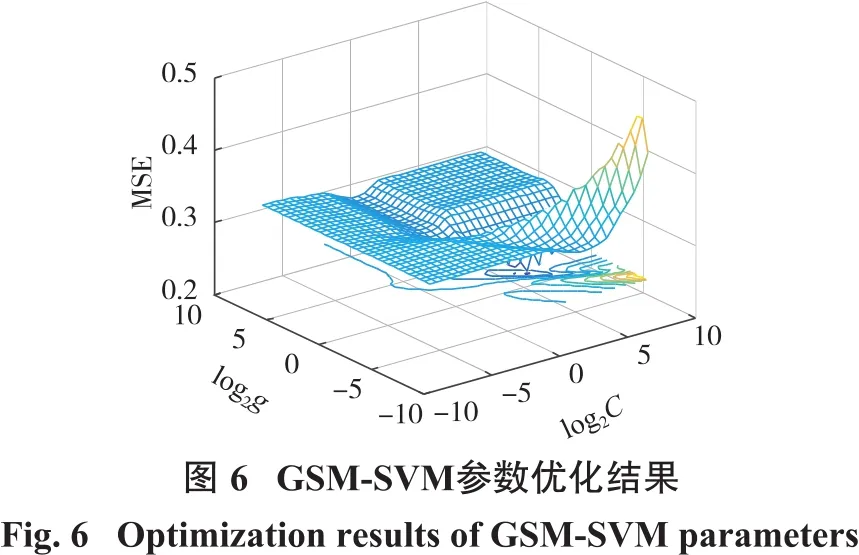
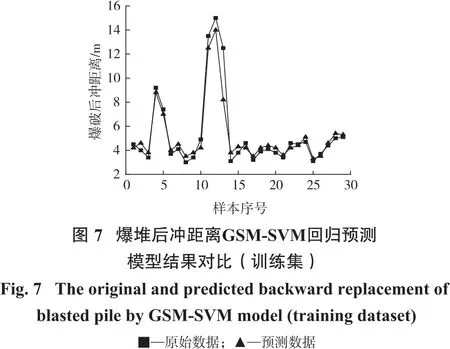
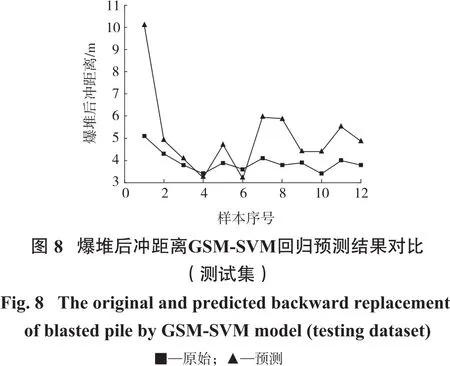
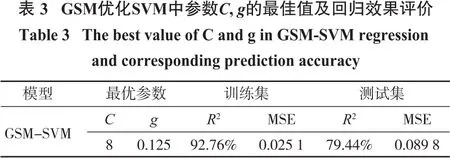
处理线性不可分问题时，将目标由低维向更高维度映射时其相关参数的挑选十分关键。常见的SVM将径向基函数纳为内置核函数，同样C和g在预测精度上发挥着至关重要的作用，其会根据上述2个参数的选取不同而异。利用LibSVM中的回归特性及Matlab实现相关的算法流程代码，交叉验证并设置阈值来获得优化后的目标参数。设定参数对C、g范围（2-8，28），交叉验证系数为10，经过模型计算后依照预测精确度最高的那组来挑选相应的参数值。根据最高精确度92.76%，确定对应的C=8，g=0.125，图6为参数优化过程示意图。由上述分析可知，该组合模型在预测爆堆后冲距离方面效果良好，能满足实际工程的需要，同时参数之间的互相解耦保证了运算可行性。图7和图8分别为真实值同训练集及训练集预测值的对比图，表3为GSM优化SVM中参数C、g的最佳值及回归效果评价结果，由图8及表3可得，模型的预测精度为79.44%，有较好的预期效果，也体现该模型在此种问题的预测方面较为可靠。

本文中提出的GSM-SVM组合模型在预测爆堆后冲距离方面有不俗的表现，同时对于将数据和变量之间的复杂关系进行封装，使得整体算法流程较为简洁，增加可读性。工程实际中收集的参数非常有限且大多属于非线性问题，GSM-SVM对于非线性问题的动态处理能力使得其更加贴合实际，更具有可操作性。尽管SVM在此类问题的预测方面效果令人满意，但是对于影响其精度的参数选取和进一步优化方面还有待提高。总体来讲，GSM-SVM组合模型在充分发挥原有模型性能的基础上，提高了对参数的全面分析和表达的能力。

2.4 结果分析

结合表2、表3可以看出，GA-SVM和GSM-SVM爆堆位移预测模型的效果都很理想，但GA-SVM更优，而GSM-SVM的预测精度相对较低，经过分析，可能是由于以下原因：①遗传算法在优化支持向量机超参数时相比网格搜索更具有优势，网格搜索有时易陷入局部最小值；②用于预测爆堆后冲距离的数据集数量比较少，增加数据集的数量有助于构建泛化能力更强的预测模型；③影响爆堆后冲距离的影响因素还有待于深入挖掘，更为科学合理的输入参数有助于产生更加精确的预测结果；④爆堆前后冲预测评估问题涉及到众多影响因素，这是一个及其复杂的高维度、非线性问题，而基于支持向量机的预测模型能够在一定程度上找寻出影响爆堆前后冲的参数与爆堆前后冲的非线性映射。

总体上来说，利用启发式算法能够快速有效地协助SVM寻找出最佳的参数组合，在提高SVM预测精度的同时也提升了速度。有鉴于此，采用支持向量机回归理论，并结合启发式算法的找寻最优解策略，能够比较真实地反映爆堆前后冲情况，为爆破参数设计提供一定的参考。当应用到工程实际中时，输入相应的输入参数值，能够通过本文已经构建好的预测模型得出一个预测的爆堆前后冲距离值，并通过调整改进输入参数的值，最终可以得出一组满足要求的爆堆前后冲距离值，防止爆堆前后冲距离过大，对其他工作面造成影响。

3 结论

（1）综合影响爆堆前后冲距离的参数，并结合SVM的工作机理，利用SVM能有效地解决爆堆前后冲的预测问题，对于爆堆前冲距离的预测采用GASVM预测模型，测试集的预测精度为99.99%，说明GA-SVM模型在预测该组数据集时具有很强的拟合能力，同时也说明影响爆堆位移的因素选择比较正确。

（2）对于爆堆后冲距离的预测采用GSM-SVM预测模型，测试集的预测精度为79.44%，训练集的预测精度为92.76%，预测精度明显不如GA-SVM模型，这可能是由于用于构建预测模型的数据集比较少，或者对影响因素的考虑不够全面造成的。

（3）在未来的研究中，可以考虑加入更多的数据集，或者是更加全面地考虑影响爆堆前后冲的因素，构建爆堆前后冲距离数据库，以便随时调用升级；另一方面，可以考虑采用更为先进的监督室学习方法和启发式算法，以构建泛化能力更强，预测精度更高的爆堆前后冲预测模型。