牵引式滑坡作用下天然气管道力学响应研究
张 杰,梁博丰,潘 波,沈坤蓉,陈林燕
(1.西南石油大学 机电工程学院,成都 610500;2.西南石油大学 南充校区,四川南充 637001)
0 引言
随着国家能源结构调整,天然气输送管道建设得到了迅猛发展。由于中国地质条件复杂,且管网规模化、密集化等特点日益突出,长输天然气管道不可避免地穿越山地、丘陵、沙漠、平原、水网等地带,容易受多种地质灾害影响,如滑坡、崩塌、水毁、沉降等,其中滑坡是影响管道安全的常见地质灾害之一。滑坡作用下天然气管道易发生破坏,造成天然气泄漏,进而引发火灾、燃爆等事故,甚至造成灾难性后果[1-2]。因此,研究滑坡作用下的管道力学响应对其安全评价、维修防护至关重要。
根据滑坡与管道的位置关系,可将其分为横向滑坡和纵向滑坡,其中横向滑坡对管道危害最为严重,图1为管道穿越横向滑坡区域示意图。当横向滑坡作用时,埋地管道将受到滑坡侧向力,其与管道铺设后的形态有着密切关系[3]。按引起滑动的力学性质可以将横向滑坡分为牵引式和推移式两类:牵引式滑坡对管道部无被动土压力,管道呈悬空状态;而推移式滑坡在发生整体滑动的情况下,下部岩土层对上部岩土层有一定的支撑作用[4]。
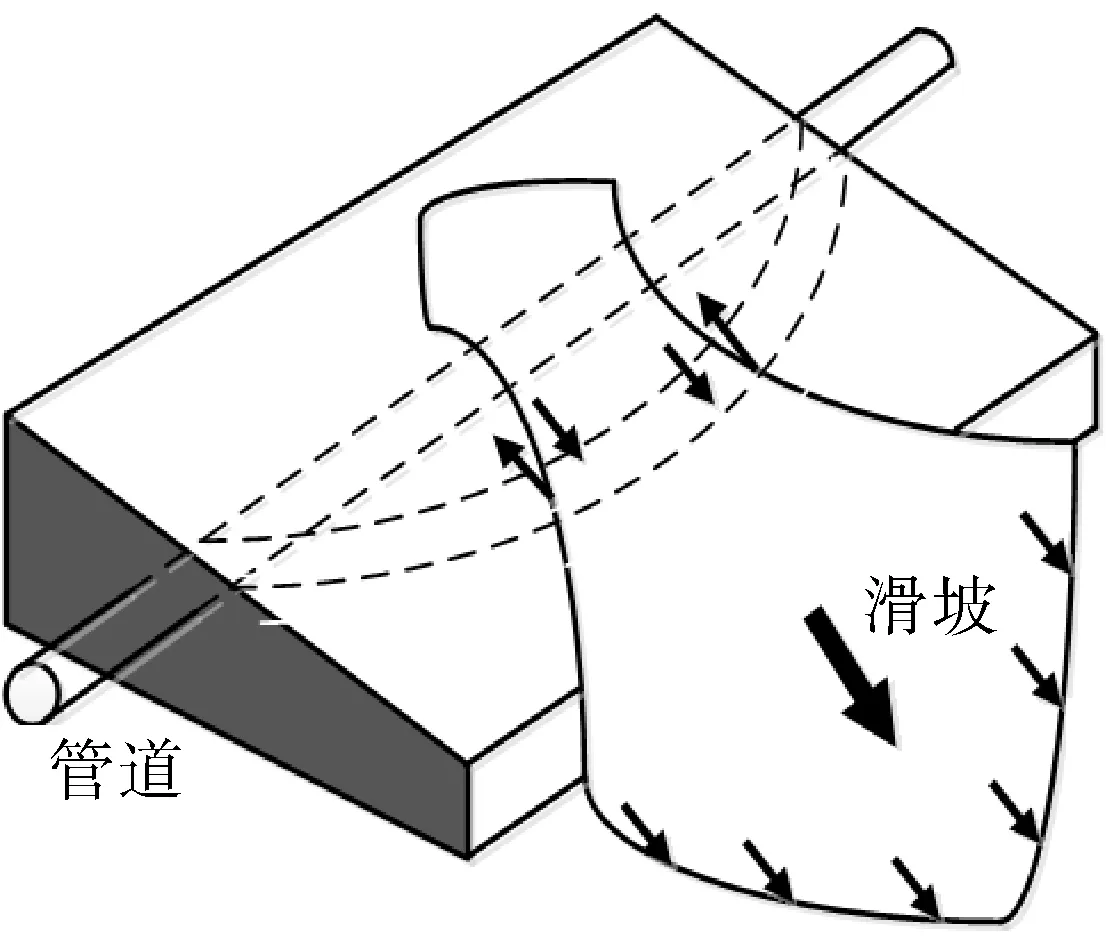
图1 管道穿越横向滑坡区示意
目前,对管道力学响应问题的研究主要是基于弹性地基梁模型开展的。如张土乔等[5]建立了垂直载荷作用下的管道纵向受力简化模型,研究了影响管道危险区应力的主要因素;邓道明等[6]分析了埋地管道在无内压和有内压作用下的内力和变形,推导出了管环弯矩和挠度的一系列计算式;袁祥忠等[7]建立了牵引式滑坡作用下管道横向受力的分段模型,采用分段模型,利用微元思想,计算出各管段的解析表达式;Zhang等[8]对滑坡区管道力学行为进行了数值仿真,探究多种参数对其力学影响,较为真实地反映出管道在牵引式滑坡作用下的形变及受力情况;Li等[3]建立了海底滑坡下推移式管道受力的分段模型,将海底管道分为4段,列出相应平衡方程,应用迭代法得出了各段解析表达式,但该模型待定系数过多,边界条件及连续性条件复杂,求解过程较繁琐。此外,大部分学者对处于埋设状态管段未作较详细分析,将悬跨段视为简支梁,忽略了非滑坡段管道变形对滑坡段管道变形的影响,使得结果误差偏大。
为此,本文提出一套改进的解析模型来描述牵引式滑坡下天然气管道力学响应问题。参照悬链线理论和大变形梁理论[9-10],得出管道在牵引式滑坡作用下的最终状态。根据边界条件,提出一种迭代的方法计算待定系数,最终得到相应的解析表达式,并在此基础上进行参数分析,以指导工程实践。
1 管道力学模型
由弹性地基梁理论[11]可知,当管道发生弯曲时,管道下方的土体也会发生微小形变,以抵抗外载作用,如图2所示。由悬链线特征可知,管道与土体在点A1处分离,其边界A1处的曲率与A1点以后有限范围(A1A2)内管道曲线曲率的符号相同,均为正号,即A0A1A2段呈现出凸曲线。A2点以后,由于滑坡作用,根据大变形梁理论可知管道呈现出凹曲线,A2点是管道曲线曲率由正变负的反曲点,该点曲率为零。管道在A3点处的侧向位移最大,曲线斜率为零。假设管道在几何及受力上都对称于y轴。

图2 滑坡下管道受力变形示意
对于管道下面土体凹陷形成的悬空段,其横向力q按式(1)计算[12],不考虑管道内介质质量。
(1)
式中D——管道外径,m;
γt——覆土容重,kg/m3;
h——覆土高度(管道中心距填土表面的深度),m;
φ——土壤内的摩擦角,(°)。
为简化假设,取横向滑坡力q为常数。
管道侧向运动时,土体响应采用理想线弹塑性模型[13],由此可得图3所示的双线性p-y关系曲线。土体抗力p以k的增长率线性增长,直到达到最大值,当其达到其最大抗力p0.1时,对应的管道位移为0.1D[14],所以在0.1D以内的土体抗力增长率为k=10p0.1/D。

图3 载荷位移关系曲线
2 控制方程
由于模型的对称性,选取管道右半段作为研究对象。该管段根据其受力情况可分为3部分,如图4所示。

图4 滑坡下管道受力变形力学模型
2.1 管段Ⅰ
管段Ⅰ处于滑床段,自管道侧向位移最大处A3点至滑床结束点A5。该管段侧向位移最大,对整体管道的安全非常重要。根据弹性地基梁理论[15-16],通过y轴方向平衡可得到控制方程:
(2)
式中E——管道弹性模量;
I——管道惯性矩;
yⅠ——管道从A3到A5的侧向位移;
T——未知拉力;
w——管道质量;
x——A4点的x轴坐标。
由式(2)可得:

(3)
式中C1,C2,C3,C4为未知系数,其中:
(4)
从而可得弯矩:
MⅠ=-EIy″Ⅰ
(5)
然后得到弹性范围内由管道轴力和弯矩造成的管道应变:
(6)
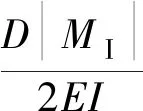
2.2 管段Ⅱ
该管段侧向土体抗力随着管道位移而发生线性变化,其控制方程为:
(7)
式(7)的解为:
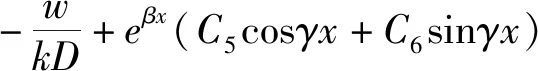
+e-βx×(C7cosγx+C8sinγx)
(x2≤x≤x3)
(8)
式中C5,C6,C7,C8为未知参数,且:
(9)
(10)
同理,可得管段Ⅱ的弯矩和应变:
MⅡ=-EIy″Ⅱ
(11)
(12)
需指出,当x≥x3时,管道侧向位移会非常小,利用A6处边界条件可知,C5和C6都非常小,为简化计算(此处对计算精度的影响极小,可以忽略不计),令C5和C6均为零。
2.3 管段Ⅲ
该管段侧向位移非常小,可以忽略。因此,可认为该管段仅受轴向土体抗力作用。轴向土体抗力可以通过将管道法向接触力wn和摩擦系数相乘得到。摩擦系数与土体性质密切相关。Bruton等[14]指出摩擦系数介于0.15~1.5之间。
远离滑坡区管道的轴向拉力逐渐减小。这部分管道末端的轴向拉力为零。其长度可以通过A6点拉力和单位管道长度受到的土体抗力得到。
3 力学模型求解
3.1 待定系数分析
所建立力学模型中共有C1,C2,C3,C4,C7,C8,T,x1,x2,x3等10个未知量。
由A5点连续性条件可知:
yⅠ∣x=x2=0.1D
(13)
yⅡ∣x=x2=0.1D
(14)
y′Ⅰ∣x=x2=y′Ⅱ∣x=x2
(15)
y″Ⅰ∣x=x2=y″Ⅱ∣x=x2
(16)
y‴Ⅰ∣x=x2=y‴Ⅱ∣x=x2
(17)
由A3及A4点的边界条件可知:
y′Ⅰ∣x=0=0
(18)
y″Ⅰ∣x=x1=0
(19)
y‴Ⅰ∣x=0=0
(20)
其中:
(21)
(22)
y‴Ⅰ=α3(C3eαx+C4e-αx)
(23)
y′Ⅱ=e-βx[C8(γcosγx-βsinγx)-C7(γsinγx
+βcosγx)]
(24)
y″Ⅱ=e-βx{C8[(β2-γ2)sinγx-2βγcosγx]
+C7[(β2-γ2)cosγx+2βγsinγx]}
(25)
y‴Ⅱ=e-βx{C8[β(3γ2-β2)sinγx+γ(3β2-γ2)
×cosγx]+C7[-γ(3β2-γ2]sinγx
+β(3γ2-β2)cosγx)]}
(26)
当滑坡作用在整个悬跨段时,管道在拉力作用下伸长量和管道几何变形Δl1相等。Δl1可以通过几何积分得到:
(27)
其中,x3是管道侧向位移非常小的位置。x3右侧管道轴向拉力T在轴向摩擦力f作用下逐渐减小,所以管道伸长量可以通过下式[17]得到:
(28)
式中A——管道截面面积。
从而有:

(29)
3.2 待定系数求解
由式(13)~(20),(29)组成方程组,包含9个方程,10个未知数,且方程形式复杂。因此,应用传统方法无法求解。根据其中参数特征,采用如下计算方法。
由式(10)可知,若要使γ存在,则有:
(30)
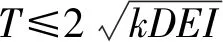
(31)
当x2到其最大值时,管道从O到x2滑坡力等于从O到x3土体抗力[4],由此可得:
qx2=p(x3-x2)
(32)
解得:
(33)
将式(21)~(26)代入式(13)~(20)得到以下方程式(考虑到滑坡力相对于管道质量很大,此处省略管道质量)。
cos(γx2)C7+sin(γx2)C8=0.1Deβx2
(34)
(35)
C2+αeαx2C3+αe-αx2C4+e-βx2(γsinγx2
(36)
α2eαx2C3-α2e-αx2C4-e-βx2[(β2-γ2)cosγx2
+2βγsinγx2]C7-e-βx2[(β2-γ2)sinγx2-2βγcosγx2]
(37)
C2+αC3+αC4=0
(38)
e-βx2{C8[β(3γ2-β2)sinγx2+γ(3β2-γ2)cosγx2]
+C7[-γ(3β2-γ2)sinγx2+β(3γ2-β2)cosγx2]}
=α3(C3eαx2+C4e-αx2)
(39)
(40)
C3+C4=0
(41)
观察式(34)~(41),可以将C1,C2,C3,C4,C7,C8,x1用x2,T和x3表示。其中x2为给定的滑坡宽度,同时假定一个x3和T,将其代入式(34),(35),(36),(37),(38),(40),(41)中,然后不断修正x3和T,首先需要使其近似满足式(17)的连续性条件,即∣y‴Ⅰ(x2)-y‴Ⅱ(x2)∣<δ1,其中δ1是一个定义的小量,为得到较高的精度,这里推荐1×10-6。由前文分析可知,将x3和T得初值设为x3max和T的最大值(由式(31)得到)。然后,将计算得到的x3和T以及其他参数代入到式(42)计算每个迭代过程中的轴向摩擦力f。
由式(29)得:
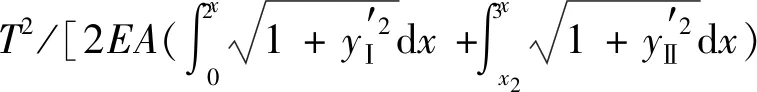
-2EAx3-2Tx3]
(42)
每次计算得到的摩擦力都需验证,以满足不等式∣f-f0∣<δ2。其中,δ2是一个定义的小量,本文推荐δ2=0.1 N/m。如果达不到δ1的精度,就需要首先对T进行修正,重新将x3和新的T代入求解;如果摩擦力的不等式不满足,就需要对轴向拉力x3进行修正,再次将新的x3和上一轮的T代入求解。当不等式满足了,最后得到的轴向拉力及其他参量即可达到标准,能够进行结果输出。需要说明的是,A6是管道侧向位移较小的位置,可取x3为较大值,以保证足够的精度。上述算法的流程如图5[18]所示。
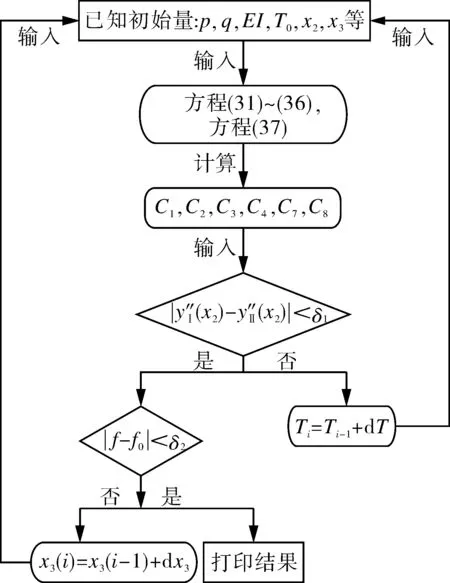
图5 算法流程
4 算例分析
为开展案例分析,表1列出了管道力学参数,表2列出了解析模型算法中需要输入的初值及误差值。

表1 管道力学参数

表2 解析模型待定系数求解参数
使用MATLAB编程,由于方程组系数矩阵存在数量级差距较大的元素,本文对系数矩阵进行截断奇异值处理,可求得管段Ⅰ和管段Ⅱ的解析表达式[19]如下:
yⅠ=-5×10-5x2+0.7469+5.56×10-9
×(e0.13x+e-0.13x)
(43)
yⅡ=103×e-0.0845x[8.0173cos(0.014x)
+2.403sin(0.014x)]
(44)
4.1 滑坡宽度
图6示出滑坡力为700 N/m时不同滑坡宽度的管道位移曲线。当滑坡宽度为140 m时,管道最大位移为1.006 8 m。随着滑坡位移增加,管道最大位移也增加。当滑坡宽度达到240 m时,最大位移为2.022 4 m。
当滑坡力为700 N/m时,不同滑坡宽度下管道总应力分布如图7所示。在弹性范围内,管道最大总应力随着滑坡宽度的增加而增加。当滑坡宽度为180 m时,最大应力为256.21 MPa;当滑坡宽度为240 m时,最大应力为290.9 MPa,相差9.69%。由图可知,应力曲线的峰值是尖锐的,没有平滑过渡区,即管道中没有塑性变形,原因是其最大应力为290.9 MPa,远低于X80的屈服极限555 MPa;管道在滑坡出应力突变,从计算模型的角度考虑,这是由于滑坡力在滑坡宽度处从700 N/m突变为0造成的。

图6 不同滑坡宽度下的管道位移曲线
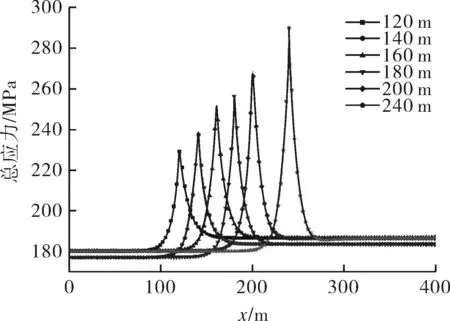
图7 不同滑坡宽度下的总应力分布
4.2 滑坡力
当滑坡宽度为180 m时,不同滑坡力作用下管道位移如图8所示。随着滑坡力增加,管道最大位移不断增大。当滑坡力为500 N/m时,管道最大位移为1.195 5 m;当滑坡力为1 000 N/m时,管道最大位移为2.299 m。最大位移增加量较为接近,即在500~1 000 N/m的范围内,管道最大位移随着滑坡力的增加而呈近似线性增加。
图9示出当滑坡宽度为180 m时,管道最大弯曲应变随着滑坡力的增大而增大的变化曲线。当滑坡力为500 N/m时,管道最大弯曲应变为2.257 7×10-4;当滑坡力为1 000 N/m时,管道最大弯曲应变为5.231 1×10-4。不同滑坡力下管道最大弯曲应变发生在滑坡宽度约180 m处,因而在滑坡末端是发生最大变形的地方,其原因是该处管道变形最大,会出现应力集中现象。因此,对于易发生滑坡区域管道,应在滑床段与非滑床段接触区域处采取保护措施。

图8 不同滑坡力下的管道位移曲线

图9 不同滑坡力下的管道应变变化曲线
4.3 管道壁厚
管道内径为0.57 m,通过外径变化来改变管道壁厚,对壁厚为0.02,0.035,0.05,0.065,0.08,0.095 m的管道进行研究。当滑坡力为700 N/m,滑坡宽度为180 m时,不同管道壁厚对管道位移影响如图10所示,可以看出,管道最大位移随着管道壁厚增加而减小。当管道外径为0.61 m时,管道最大位移为2.299 m;当管道外径为0.76 m时,管道最大位移为1.195 5 m。
随着管道壁厚增加,管道最大位移不会无限减小。在方程有解的前提下,即在一定管道壁厚范围内,当管道壁厚增加到一定值时,管道最大位移减小量逐渐降低,最大位移逐渐接近一定值。图11示出由最大位移组成的曲线呈微弱凹曲的形态,这是由于随着壁厚增加,管道刚度增加,其更容易抵抗外力并减少自身变形造成的。
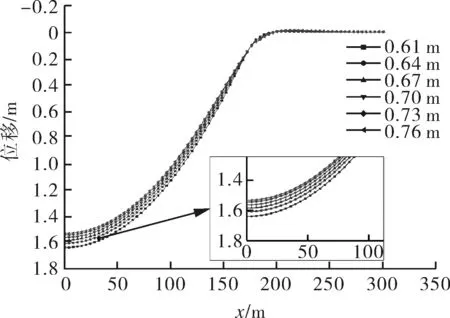
图10 不同外径管道位移曲线
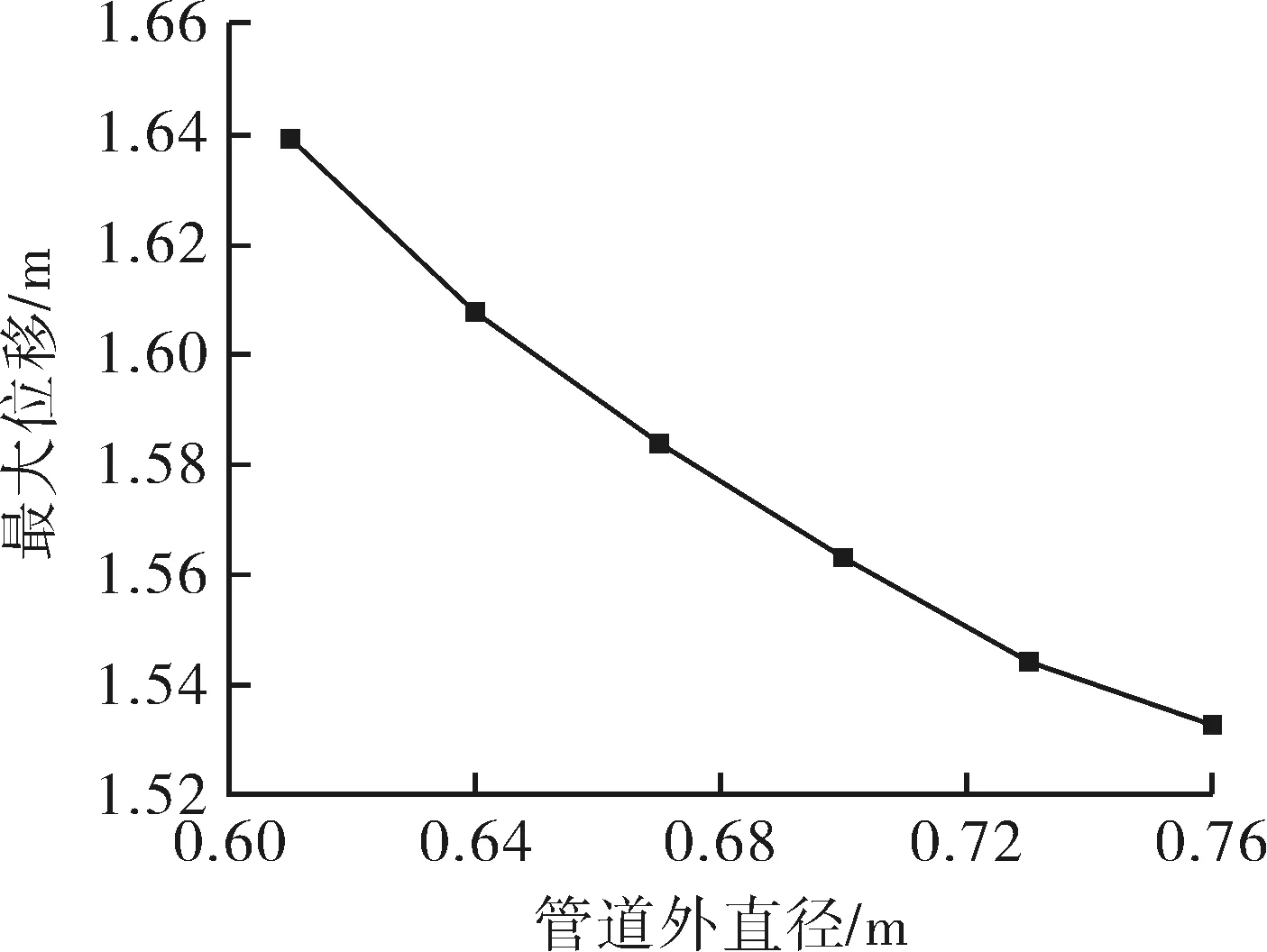
图11 不同外径管道最大位移变化曲线
当滑坡力为700 N/m,滑坡宽度为180 m时,不同外径管道弯曲应变分布如图12所示。

图12 不同管道外直径下的管道弯曲应变曲线
由图12可看出,随着管道厚度增加,管道最大弯曲应变呈下降趋势。当管道外径为0.61 m时,最大弯曲应变为3.31×10-4;当管道外径为0.76 m时,管道最大弯曲应变为1.902×10-4。这种现象在管道最大弯曲应变中更明显,其原因与上述相同。管道最大弯曲应变增长率的绝对值降低;同时,管道最大弯曲应变出现在滑坡末端,因此应特别注意确保该段管道安全运行。
5 结论
(1)本文考虑了悬链线和大变形梁的特点,详细分析了牵引式滑坡段管道的形态特征,保证所建立模型的准确性。该模型的边界条件增加,连续性条件减少,方程形式简单,需要求解的待定系数从10减少到7。结合本文提出的迭代算法,降低了整个解析求解难度,提高了求解效率。
(2)探讨了滑坡宽度,滑坡力和管道厚度等参数对管道力学响应影响。分析表明,滑坡宽度的增大加剧了管道变形,使管道更容易破坏。因此,在铺设管道时,应采取措施防止滑坡段扩张,并对滑床与非滑移段接触部位的管道采取保护措施,同时通过增加管道壁厚也可降低其失效概率。

