控制棒驱动机构备件数量优化方法
肖丽丽,靳峰雷,谷继品
(中国原子能科学研究院 反应堆工程技术研究部,北京 102413)
控制棒驱动机构是反应堆本体中关键的动设备,其功能是通过改变控制棒在堆芯中的位置来调节反应堆的反应性[1]。控制棒驱动机构能实现对反应堆指定功率水平的保持、停堆和再次临界状态的转换,是反应堆控制保护系统的重要组成部分。控制棒驱动机构能否安全、可靠地运行直接影响反应堆的可运行性。
在某些类型的反应堆上,当某台控制棒驱动机构出现故障时,为提高反应堆的经济性,需立即拆下并更换新备件,以保证反应堆的正常工作。由于控制棒驱动机构成本较高,备件贮存量多,总费用高;备件贮存量少,又可能造成缺少备件而影响反应堆的安全。如何合理确定备件数量对于提高控制棒驱动机构系统的运行可靠性具有重要意义。
近年来,国内有关部门和科研人员非常关注备件需求分析方面的研究,进行了许多理论分析,编制了相应的国家军用标准[2-5],这些标准为备品备件的需求分析提供了程序及理论支持。研究者发表了大量关于备件方面的论文[6-10],为备件数量的确定提供了良好的理论基础。其中有备品备件需求确定方法的探讨[6-7]、考虑部件已工作时间的备件计算模型[8]、基于备件保障率的备件运行量模型[9],还有的考虑了备件满足率[10]。目前文献中关于备件的确定方法多数是通过直接计算得到的,很少涉及建立优化模型,给出备件数量的优化算法。针对在不同使用条件下的不同设备,如何建立相应的优化模型,经济合理地确定备件数量尚未解决。
本文针对控制棒驱动机构,在系统连续运转时间不小于换料周期的情况下,提出一种分组备件数量优化方法,给出总费用最少的各子系统的备件配置方案。
1 备件分析模型
在备件分析中常用系统连续运转时间[11]来确定备件设置量。对于单一系统,可直接计算。然而,当1个系统由几个子系统组成时,各子系统的备件如何配置就要考虑经济问题。如在一定费用的情况下,找出系统连续运转时间最长的子系统配置方案,或在系统连续运转时间一定的情况下,找出总费用最少的各子系统的备件配置方案[11]。实际应用中,后一种情况较常见,本文仅考虑该情况。
假设系统由s个子系统组成,各子系统均由多台同样的设备组成,设备单价分别为c1,c2,…,cs,配置的备件数量分别为n1,n2,…,ns,各子系统的连续运转时间分别为T1,T2,…,Ts,系统的连续运转时间为T。如果要求系统连续运转时间至少为T0,当各子系统是串联结构时,相应于总费用最少的优化模型为:
(1)
其中,子系统i的连续运转时间[11]为:
(2)
Ki=μi/miλi
(3)
式中:mi、ni分别为子系统i所含设备数量及所需备件数量;Ki为子系统i的系统故障修复率和故障率之比;λi、μi分别为子系统i中单台设备的故障率和故障修复率,i=1,2,…,s。
2 控制棒驱动机构备件
在某快堆电站,控制棒驱动机构系统由安全棒驱动机构(safety rod drive mechanism, SaRDM)和补偿调节棒驱动机构(shim rod drive mechanism, ShRDM)两套独立的停堆子系统组成。安全棒驱动机构子系统有7台安全棒驱动机构,补偿调节棒驱动机构子系统有21台补偿调节棒驱动机构。为保证反应堆的安全运行,仅当两套停堆系统均处于正常工作状态时,才能开启反应堆。故在分析控制棒驱动机构的备件时,两套停堆子系统作为串联模型来考虑,并且每套停堆子系统也是串联模型。
该快堆电站计划每180 d(4 320 h)进行换料,需保证系统连续运转时间不少于180 d。在换料期间,可增派人力维修,使得在再次开堆时,备件数量仍达到初始数值,保证180 d内不会因为控制棒驱动机构缺少备件而影响反应堆的安全性。经调研,单台安全棒驱动机构的成本约为400万元,单台补偿调节棒驱动机构的成本约为350万元。
根据某快堆的实际运行经验,单台控制棒驱动机构的平均故障间隔时间(MTBF)初步确定为4 400 h,平均修复时间(MTTR)预估为200 h。假设控制棒驱动机构的寿命及修复时间均服从指数分布,则相关信息列于表1。

表1 控制棒驱动机构相关信息
注:故障率中“/”上面数字为设备数量、下面数字为单台设备的MTBF;故障修复率为MTTR的倒数
代入控制棒驱动机构的具体数值,通过MATLAB软件求解上面的优化问题(s=2),计算结果为:需配备安全棒驱动机构备件3台,补偿调节棒驱动机构备件16台,系统连续运转时间4 466.8 h,备件总费用6 800万元。在实际应用中,该结果难以接受。造成这样结果的一个原因在于两套停堆子系统的K相差较大,从而影响了最终的备件数量。
3 分组计算备件模型
为减少备件数量,根据各子系统的K,本文提出了分组计算备件模型。本例中,两个子系统的K比为K1/K2=3,K相差较大。为降低各子系统的K差别,可将K较小的子系统分成2组,相当于增加了子系统的个数,设分组后第i组含设备数m2i台,备件数为n2i台,K为K2i,连续运转时间为T2i,i=1,2,即数学模型变为:
(4)
其中,
(5)
(6)
若上述优化问题有不止1组解,则取系统连续运转时间最长的那组解,即优化问题变为:
maxf1=Ts
(7)
针对本文具体实例,将21台补偿调节棒驱动机构分成两组,共有10种情况,分别求出各种情况下的费用最少解,所得结果列于表2。
由表2可知,最少费用是3 950万元,有4组解,选系统连续运转时间最长的第1组解为分成2组时的最优解。从该解可看出当两组数量较接近时,能取到最优解。
3.1 前提条件
参照上面实例,系统中包括7台安全棒驱动机构及21台补偿调节棒驱动机构,用MATLAB生成几组安全棒驱动机构及补偿调节棒驱动机构的MTBF及MTTR,然后分别求解使用常规算法及分组算法时的优化结果,所得结果列于表3。
从表3可看出,并不是所有情况下分组计算结果均优于常规计算结果,1B结果优于1A,即本文中所采用的实例,而2B、3B结果劣于2A、3A。通过分析,可知情况1A满足如下3个条件:1) 子系统所含设备数m1
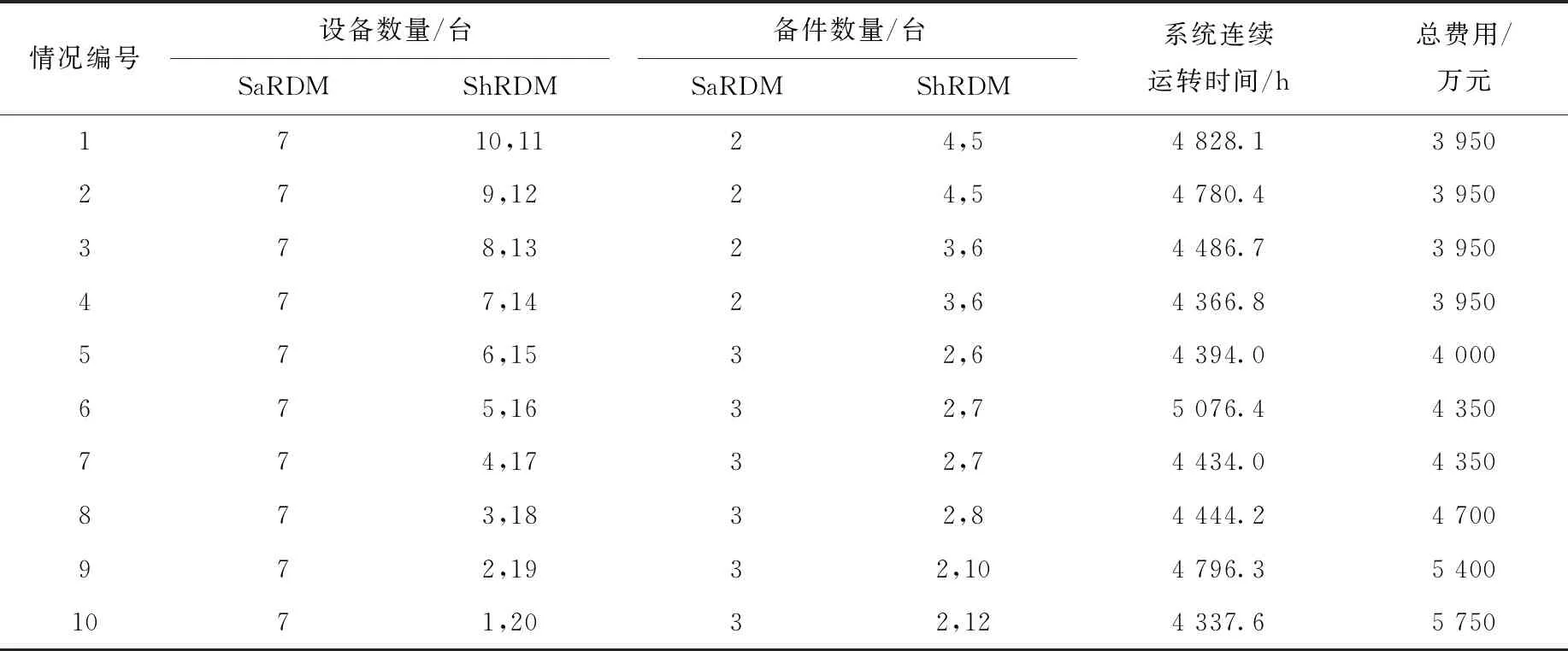
表2 分组后备件需求量
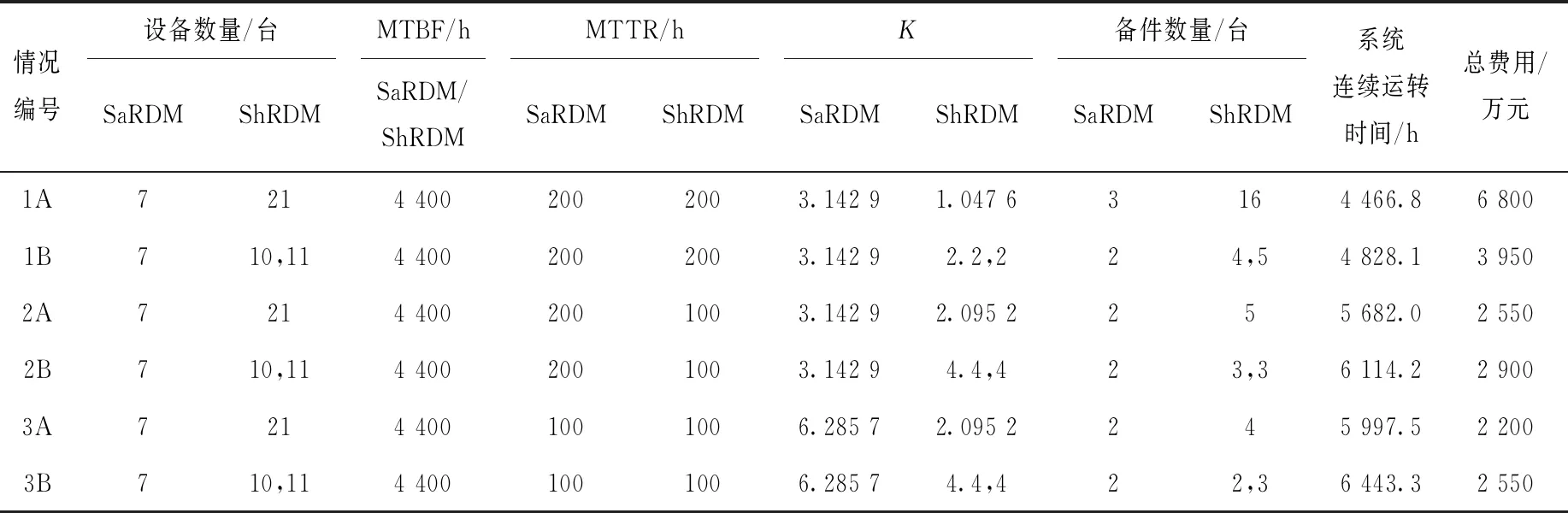
表3 常规算法与分组算法备件需求量
注:A情形为常规算法,B情形为分组算法
本文采用计算机模拟方法,对于1个由2个子系统组成的系统,随机生成每个子系统相应的单台设备的MTBF、MTTR、成本、所含设备数量及系统连续运转时间T0,即每组随机数是具有如下形式的数组:(MTBF1,MTTR1,MTBF2,MTTR2,c1,c2,m1,m2,T0),然后分别按常规算法及分组算法求解优化问题,再比较备件费用。
首先,将同时满足上述3个条件的随机数组集合记为D,记D中元素个数为p;再计算D中分组优化结果优于常规算法结果的元素个数,记为q,同时将两种算法所得费用相同的情形个数记为w;最后计算相应比值。每次生成10 000组随机数,共进行10次随机模拟(在不同次模拟中,各变量分布函数不同),计算结果列于表4。表4 中,r1(r1=q/p×100%)表示分组算法优于常规算法的随机数组所占的百分比,r2(r2=(q+w)/p×100%)表示分组算法不劣于常规算法的随机数组所占的百分比。
从表4可看出,满足上述3个条件,分组计算结果经常优于常规算法。检查分组计算结果劣于常规算法的情况,发现多数常规算法中子系统1备件数n1=1,于是在随机模拟计算中增加1个条件,即将n1≠1当成条件4,重复上述步骤,仅由3个条件改成4个条件,进行10次随机模拟,计算结果列于表5。
从表5可看出,对于同时满足4个条件的随机数组,通过MATLAB计算,在两种算法均有解的情况下,分组计算结果多数均优于常规算法的。
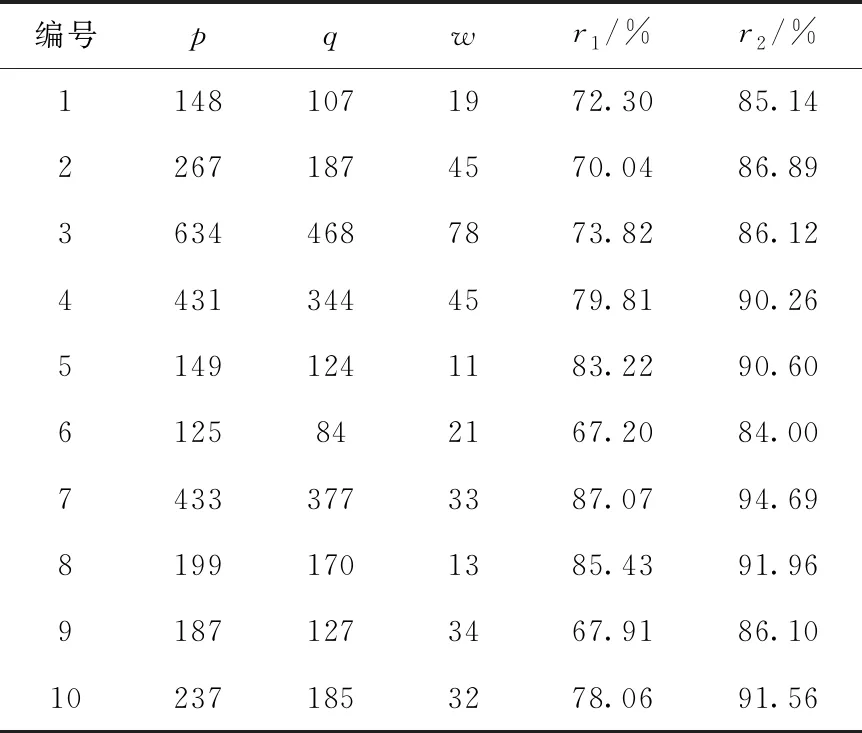
表4 满足3个条件时随机模拟结果
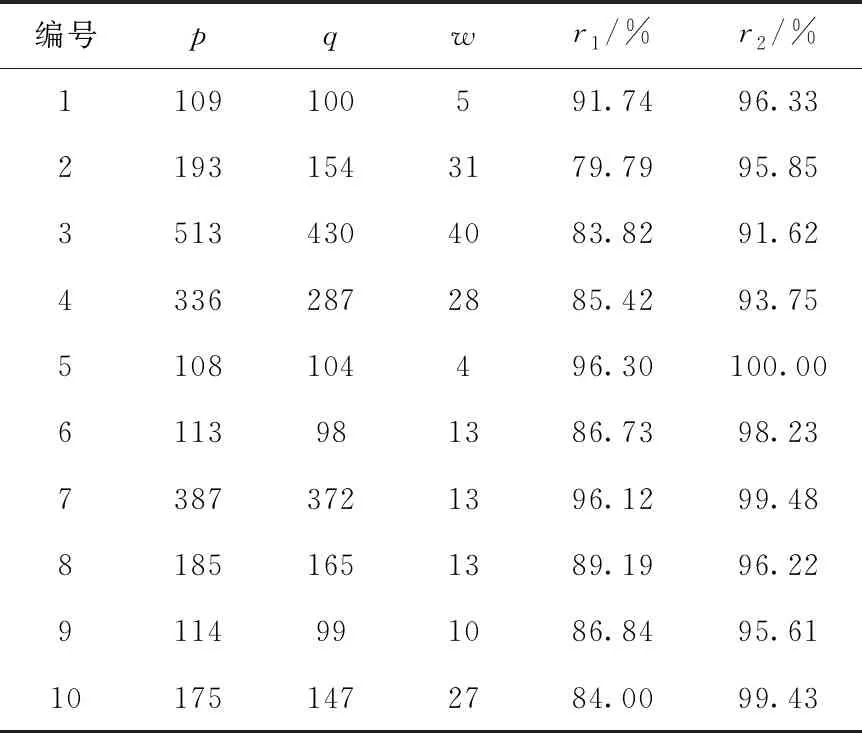
表5 满足4个条件时随机模拟结果
3.2 分组数量
选择分成两组而不是更多组的原因在于:
1) 两个子系统的K1/K2=3,为降低各子系统的K差别,可将K较小的子系统分为2组或3组,如果分成更多组,则另一子系统K反而成为较小值,成为薄弱环节;
2) 增加分组,不同子系统在极短的瞬间有可能同时出现故障,需立即能采取维修措施,隐含了增加维修资源的信息,所以分组数不宜过多,否则很难保证能有足够的维修资源可使用;
3) 如果分成2组能得到可接受的结果,则不考虑分成更多组的情况。
3.3 原因分析
分析分组后备件数量会变少的原因,文献[11]给出的系统连续运转时间公式的前提是:在系统投入运转(启动)后,将随着系统在运转过程中,故障的发生和故障备件的修复出现状态转移,如果故障的发生和修复均是独立事件,这样在极短的瞬间将不会出现两个或更多的事件,那么在系统连续运转过程中由于故障的发生和修复所导致的状态转移仅能出现在两个相邻状态间。当1个系统中包含多个子系统时,每个子系统中均满足该前提。
本文提出的分组备件优化模型,增加分组后,相当于增加子系统,那么不同子系统在极短的瞬间有可能出现两个或更多的事件,增加了状态转移的可能情况。分组后,一旦出现故障,能立即采取维修措施,隐含了增加维修资源的信息。分组模型考虑了2台补偿调节棒驱动机构同时发生故障、需修复的情况,并假设维修效率保持不变,即修复2台补偿调节棒驱动机构所需时间和修复1台补偿调节棒驱动机构所需时间相同。这就是分组后备件数量会减少的原因。
只有在2台补偿调节棒驱动机构同时出现故障时,才会用到新增的维修资源,平时不需增加维修资源。这在实际中是可行的,一旦同时出现故障,可临时调派有经验的维修人员进行维修。
4 结论
当计算1个含有2个子系统的复杂系统的备件需求量时,如果满足如下4个条件:子系统所含设备数m1
1) 由于实际上并不存在人为的分组,故分成两组的备件可通用,从而系统平均运转时间可能较计算值大。
2) 分组后备件需求量能减少,这是由于分组时增加了状态转移的可能情况,隐含了增加维修资源的信息,并且新增的维修资源与原有维修资源的工作效率相同。即分组模型考虑了2台补偿调节棒驱动机构同时失效和修复的情况,并假设2台补偿调节棒驱动机构失效修复所需时间和1台补偿调节棒驱动机构失效修复所需时间相同。如果有关于维修资源的费用信息,也可将相关费用增加到目标函数中,求出相应的最优解。
3) 实际应用中,根据K的差别进行分组,未必一定要分成2组,可先分成2组计算,如果所得备件数量仍难以接受,根据实际能增加的维修资源情况,再试着分成3组或更多组,然后从中选出最优的结果。
4) 该研究方法也可用于其他设备备件的分析,对工程中设备备件的分析与研究具有指导意义。
5) 后续工作可从优化模型出发,分析具体原因,以期进一步指导分组算法的工程实践和备件的配置方案。

