直接布雷顿循环气冷反应堆系统运行特性分析

明 杨，易经纬，方华伟，刘 凯，赵富龙,*，谭思超，田瑞峰

(1.哈尔滨工程大学 核安全与仿真技术国防重点学科实验室，黑龙江 哈尔滨 150001;2.中国核动力研究设计院，四川 成都 610213)

布雷顿循环反应堆是第4代核能系统的优先发展堆型之一[1]。该堆型通常采用化学性质稳定、热工性能良好的气体冷却剂(如氦气、氙气等)，堆芯冷却剂出口温度可达1 000 ℃甚至更高[2]，其主要特点是固有安全性高、经济性好、发电效率高、工艺热应用广泛[3]。

布雷顿循环系统分析程序方面，国内外已开展了很多研究。成利等[4]利用simulink程序，对核电站反应堆温度控制系统进行建模，验证动态系统的建模方法可行性。李海鹏等[5]采用集总参数的建模方法，建立了HTR-10系统的动态模型，结果能正确反映系统的正常运行特性。唐丽丽[6]针对燃气轮机布雷顿循环进行了建模仿真，研究了压气机与气轮机的运行特性。王恩华等[7]针对布雷顿循环氦气轮机的起动过程进行了动态仿真，得到了压气机和透平的工作曲线。解衡等[8]开发了仿真程序，对布雷顿循环负荷丧失事故工况以及主换热器换热量减少两种瞬态工况进行了仿真。李文龙等[9]开发出布雷顿循环的瞬态分析软件，针对引入反应性、工质质量流量变化等工况进行了仿真研究。Wright等[10-11]基于simulink程序首先针对闭式布雷顿循环建立了系统分析程序，分析系统的变工况特性，并在已有程序基础上引入控制，研究不同控制方法下系统的响应特性。Verkerk[12]针对布雷顿循环，预测了布雷顿循环在反应堆变功率工况下的动态变化。Becker等[13]采用计算流体动力学软件CFX-4建立了高温气冷堆传热流动的三维数值仿真模型，进行了稳态和瞬态仿真计算与分析。Tauveron等[14-15]开发出一维计算机仿真程序CATHARE对布雷顿循环进行安全性分析，并对系统破口事故进行了仿真。Saez等[16]利用CATHARE程序对布雷顿循环的气轮机组通流阻塞情况进行了仿真研究。Bentivoglio等[17]应用CATHARE程序对德国OberhausenⅡ50 MW直接布雷顿循环核电站进行了仿真研究。

调研发现，国内外学者进行了诸多关于布雷顿循环反应堆系统的仿真分析研究，并进行了系统运行特性的分析以及参数优化，但针对小型直接布雷顿循环反应堆系统分析程序的相关研究较少。此外工质物性模型多为常物性，对系统变工况运行时的仿真能力存在一定的不足[10-11]。因此本文针对小型直接布雷顿循环反应堆系统建立系统分析程序，并建立精确的工质物性数据库，考虑工质变工况时的物性变化，开展小型布雷顿循环系统稳态工况仿真以及反应堆升降功率、引入阶跃反应性、关键设备参数变化、机组甩负荷等瞬态工况下的动态仿真。

1 系统分析程序建模

1.1 建模方法及假设

建模对象为一种以氦氙混合气体作为工质的小型气冷快堆，系统循环方式为直接布雷顿循环，其原理如图1所示，相应的一维系统分析程序基于图1建立，子模块功能和布置与系统图基本相同，旨在尽可能还原系统的真实运行过程。

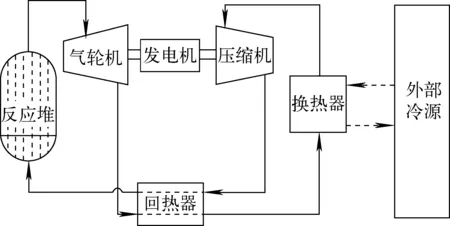
图1 直接布雷顿循环气冷反应堆系统原理图

基本建模思路为：1) 依据布雷顿循环各重要设备的热力学特性、流体力学特性、转动特性等逐步建立各设备的数学物理模型，基于质量守恒、能量守恒、转子功率平衡等原理，构造各重要设备共同运行的数学物理关系；2) 通过数值方法对模型进行求解，获得主要设备不同工况下的运行数据，模拟布雷顿循环的实际工作过程，并加入相应的控制方法，尽可能复现布雷顿循环的实际工作状态。

建立的系统分析程序包括8个子模块：反应堆模块、气轮机模块、压气机模块、回热器模块、冷却器模块、转子模块、流量变化模块、PID控制模块。

各子模块内部的计算公式、自定义函数、物性数据库、曲线插值方法等实现了每个子模块的计算功能，选取合适的初始参数与求解算法，进而完成布雷顿循环的系统分析计算。为简化数学物理模型，基本假设如下：1) 工质为实际气体，在关键设备内一维流动，忽略工质物性在空间上的不均匀性；2) 忽略工质泄漏，系统在运行时与外界环境无质量与能量的交换；3) 忽略转动部件运行时摩擦导致的能量损失；4)忽略长期运行对换热系数、局部阻力系数等参数的影响。

1.2 关键设备物理模型

1) 反应堆模型

反应堆是布雷顿循环的能量来源，反应堆模块需在各工况下正确计算反应堆的进出口工质温度、压力以及反应堆功率，同时反映反应堆的温度反馈与核反馈等物理过程。由于在系统动态过程中，主要关注反应堆功率变化以及中子通量变化，因此选取点堆中子动力学方程，主要方程如下：

(1)

(2)

(3)

ρ=ρin-α(Tf-Tf0)

(4)

式中：N堆为反应堆热功率；ρ为总反应性；β为总缓发中子份额；βi为第i组缓发中子份额；Λ为中子代时间；λi为第i代缓发中子衰变常量；Ci为缓发中子先驱核浓度；ρin为控制棒引入的反应性；α为温度负反馈系数；Tf为核燃料温度；Tf0为额定功率下燃料温度。

堆芯传热模型基于集总参数法建立，由于堆芯传热模型关心反应堆的出口温度与堆芯功率的关系，可认为整个堆芯的燃料元件在同一时刻均处于同一温度。模型主要方程如下：

(5)

G堆cp冷(T堆冷o-T堆冷i)]

(6)

(7)

式中：Pr为反应堆热功率；Tf为燃料平均温度；ρf为燃料元件密度；cvf为燃料元件热容；Vc为反应堆总体积；α为燃料元件换热系数；A为燃料元件换热面积；ρ冷为冷却剂密度；cp冷为冷却剂比定压热容；T堆冷a为堆芯冷却剂平均温度；T堆冷o为堆芯冷却剂出口温度；T堆冷i为堆芯冷却剂进口温度；ε为堆芯孔隙率；G堆为堆芯质量流量。

2) 气轮机与压气机模型

由于系统需计算气轮机与压气机的变工况运行特性，准稳态法不适用于偏离稳态工况较大的计算，因此系统分析程序采取特性曲线插值法对气轮机进行建模。气轮机模型主要方程如下：

δ气=T气i/T气o

(8)

(9)

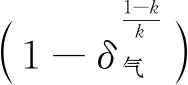
(10)

式中：G气为气轮机质量流量；T气o为气轮机出口温度；T气i为气轮机进口温度；δ气为气轮机膨胀比；n为气轮机转速；η气为气轮机等熵效率；N气为气轮机功率；k为绝热指数。

系统分析程序采取特性曲线插值法对压气机进行建模。压气机模型主要方程如下：

ε压=T压o/T压i

(11)

(12)

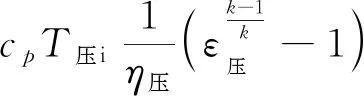
(13)

式中：G压为压气机质量流量；T压o为压气机出口温度；T压i为压气机进口温度；ε压为压气机压缩比；η压为压气机等熵效率；N压为压气机功率；k为绝热指数。

3) 回热器与冷却器模型

回热器模型基于其结构和换热方式对其建模，并作一定程度的假设，忽略回热器与外界的换热，认为同一截面内工质的温度、速度、压力参数一致，流体沿轴向一维流动，主要方程如下:

G低i=G低o=G压

(14)

G高i=G高o=G气

(15)

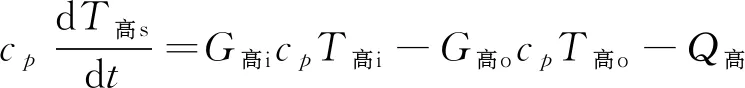
(16)

T高s=(T高o-T高i)/2

(17)

(18)

(19)

式中：G高i为回热器高温侧进口质量流量；G高o为回热器高温侧出口质量流量；T高i为回热器高温侧进口温度；T高o为回热器高温侧出口温度；G低i为回热器低温侧进口质量流量；G低o为回热器低温侧出口质量流量；T低i为回热器低温侧进口温度；T低o为回热器低温侧出口温度；Q高为回热器高温侧换热量；Q低为回热器低温侧换热量；M高为回热器高温侧流体总质量；M低为回热器低温侧流体总质量；a高、a低为回热器换热系数；A高、A低为回热器换热面积；e高、e低为回热器换热面效率。冷却器模型与回热器模型类似。

4) 转子模型

转子模型建立基于假设3，忽略转动部件间的摩擦。系统处于稳态运行时，转子力矩平衡，气轮机转速维持恒定。当气轮机的输出功与压气机耗功不等时，转子将在力矩的作用下加速或减速。转子模型主要方程如下：

(20)

n=30ω/π

(21)

式中：ω为转子角速度；Ne为系统电功率；Nt、Nc为气轮机、压气机功率；I为转子转动惯量；n为压气机转速。

5) 压降模型

气体冷却剂在管道中的压降采用沿程摩擦压降进行计算，文中采取经典的Darcy公式，选取合理的摩擦系数，确定流道的水力直径、通道长度等参数即可计算管道中的压降与关键设备中的压力变化情况，主要方程如下：

(22)

式中：Δpf为压降；f为摩擦系数，它与流体的流动性质、流动状态、受热情况、流道的几何形状、表面粗糙程度相关；ρ为工质密度；L为通道长度；De为流道水力直径；V为体积。

6) 物性模型

首先查询工质在系统运行温度、压力范围内的绝热系数、比热容、密度，并在系统分析程序中生成数据库。之后定义插值函数的计算方法，在计算过程的每个时间步长内实时更新物性参数。

2 计算结果分析

2.1 稳态计算结果分析

对布雷顿循环系统在额定工况下稳态运行进行计算，并将计算结果与系统设计值进行对比后求出仿真误差，结果列于表1。可看出在布雷顿循环系统额定工况的仿真过程中最大仿真误差为6.38%，计算结果较为合理，说明开发的系统分析程序可靠，可继续进行布雷顿循环系统变工况条件下的动态分析。

2.2 瞬态计算结果分析

1) 引入反应性工况

在布雷顿循环的变工况运行过程中，反应堆会由于控制棒的动作或其他原因而引入反应性，会导致反应堆的功率发生变化，从而引发整个系统运行参数的较大波动，因此引入反应性是探究系统特性的重要工况之一。计算初始反应堆在设计工况下运行，1 000 s时引入100 pcm的正反应性，而后在2 000 s时引入100 pcm的负反应性，其他输入变量保持额定运行值不变，对系统各关键参数进行仿真，总仿真时长为3 000 s。

反应堆出口温度、核燃料温度的动态变化如图2所示。引入正反应性导致中子通量与反应堆热功率迅速升高，导致堆芯核燃料与反射层温度上升。由于反应堆的核反馈与温度反馈作用，等同于向反应堆引入了负反应性，以此来抑制核燃料和反射层温度的上升，工质出口温度与核燃料的响应曲线会呈波动变化并逐渐平稳。引入负反应性时与引入正反应性时功率趋势相反。

图3为关键设备功率曲线。由图3a可看出，引入正反应性时，反应堆功率峰值达到11.8 MW，随后在燃料温度效应、慢化剂温度效应等物理现象的影响下出现负反馈，并迅速下降。之后呈现功率高低震荡现象，并最终趋于稳定，功率提升至10.5 MW。引入负反应性时，反应堆功率谷值达到8.0 MW，随后在反应堆的自稳调节作用下出现回升，之后呈现功率高低震荡现象后稳定，功率降至9.6 MW。由图3b、c、d可看出，引入正反应性后反应堆功率的上升导致工质出口温度升高，同时气轮机做功功率提升，从而使转子转速提升。同时压气机功率也相应升高，发电机功率由额定工况下的2.63 MW增至2.71 MW，布雷顿循环系统的功率输出能力提升。

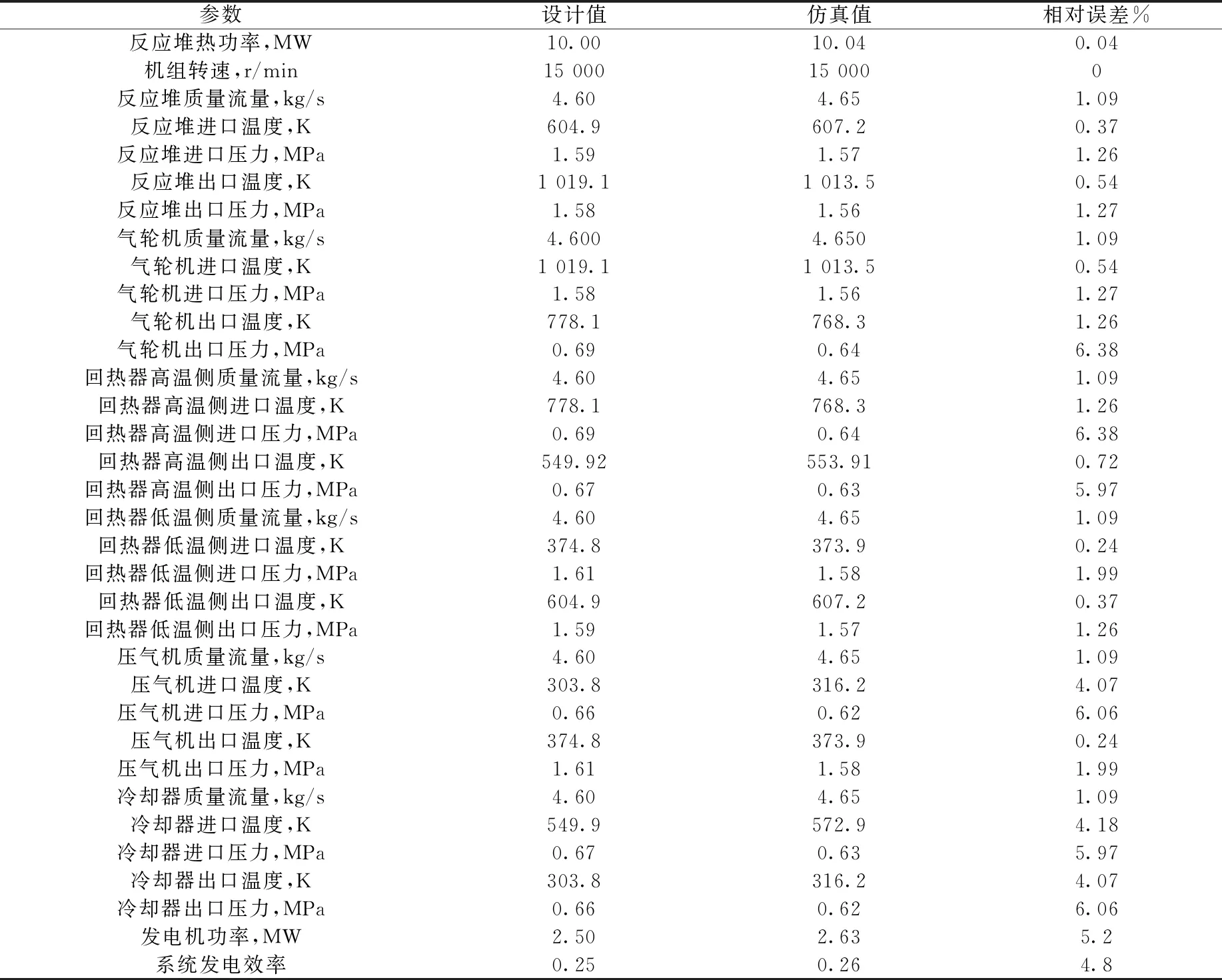
表1 额定工况仿真结果

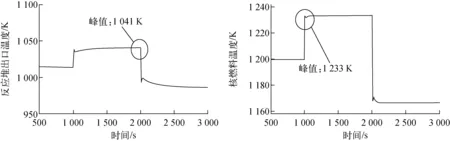
图2 反应堆出口温度与核燃料温度曲线

图3 关键设备功率曲线

2) 温度阶跃变化工况

初始系统运行稳定，在2 000 s时堆芯进口工质温度由604.9 K阶跃上升至620 K，其他输入变量保持额定值不变，对系统进行仿真，总仿真时长为4 000 s。反应堆出口温度、反应堆核燃料温度和反应堆功率的计算结果如图4所示。

从图4可知，反应堆进口工质温度阶跃升高，由于工质与堆芯以及反射层间的换热量下降，堆芯燃料温度与反射层温度上升，由于堆芯温度具有负温度反应性系数，因此引入负反应性，导致反应堆功率下降，进而使反应堆功率降低，同时堆芯燃料温度也进一步降低。反应堆功率、堆芯燃料温度和反应堆出口温度的响应曲线会呈先升高后降低的波动变化，并逐渐趋于稳定。

3) 流量阶跃变化工况

在2 000 s时反应堆进口工质质量流量由 4.60 kg/s阶跃降至4.50 kg/s，其他输入变量保持额定值不变，对系统进行仿真，总仿真时长为4 000 s。反应堆出口温度、核燃料温度和反应堆功率仿真结果如图5所示。反应堆进口氦气质量流量阶跃下降，工质与堆芯及反射层间的换热量下降，导致堆芯燃料温度与堆芯反射层温度上升。由于堆芯核燃料具有负温度反应性系数，温度升高导致引入负反应性，导致反应堆功率下降，进而导致反应堆出口温度与核燃料温度的回落。反应堆出口温度、核燃料温度和反应堆功率的响应曲线会呈先上升后下降的波动变化，并逐渐趋于稳定。

图4 温度阶跃变化工况下反应堆出口温度、核燃料温度、反应堆功率曲线

图5 流量阶跃变化工况下反应堆出口温度、核燃料温度、反应堆功率曲线

4) 气轮机组甩负荷工况

在布雷顿循环的变工况运行过程中，可能出现气轮机组甩负荷情况，即发电机转子与气轮机组转子脱扣，气轮机组失去载荷的工况，系统运行参数会因此产生较大的波动。因此本节将着重研究甩负荷工况下的系统响应特性。初始系统运行稳定，在2 000 s时堆芯进口工质温度由604.9 K阶跃升至 620 K，其他输入变量保持额定值不变，对系统进行仿真，总仿真时长为4 000 s。

转子转速、反应堆功率和反应堆出口温度的计算结果如图6所示。由于气轮机组失去载荷，与发电机脱扣，导致转子转速由15 000 r/min迅速飙升至16 200 r/min。系统工质质量流量迅速增大，导致冷却剂从反应堆带走的热量增加。反应堆出口温度在流量的增加作用下迅速降低，同时由于温度反馈的作用，反应堆功率增高。这种反应堆功率的迅速升高对布雷顿循环系统的影响十分严重，可能导致严重事故的发生。由程序计算结果显示，系统对转子引入转速控制是极其必要的。

加入转速控制后的转子转速、反应堆功率和反应堆出口温度的计算结果如图7所示。控制系统相当于为气轮机组加入引入的负载，当转子转速超过限值后对转子进行刹车从而减少转速，将转子减速到15 370 r/min，从而抑制系统质量流量的增加，并且控制反应堆功率在11 MW左右，从而控制反应堆功率在安全范围内，防止极限工况与事故发生。

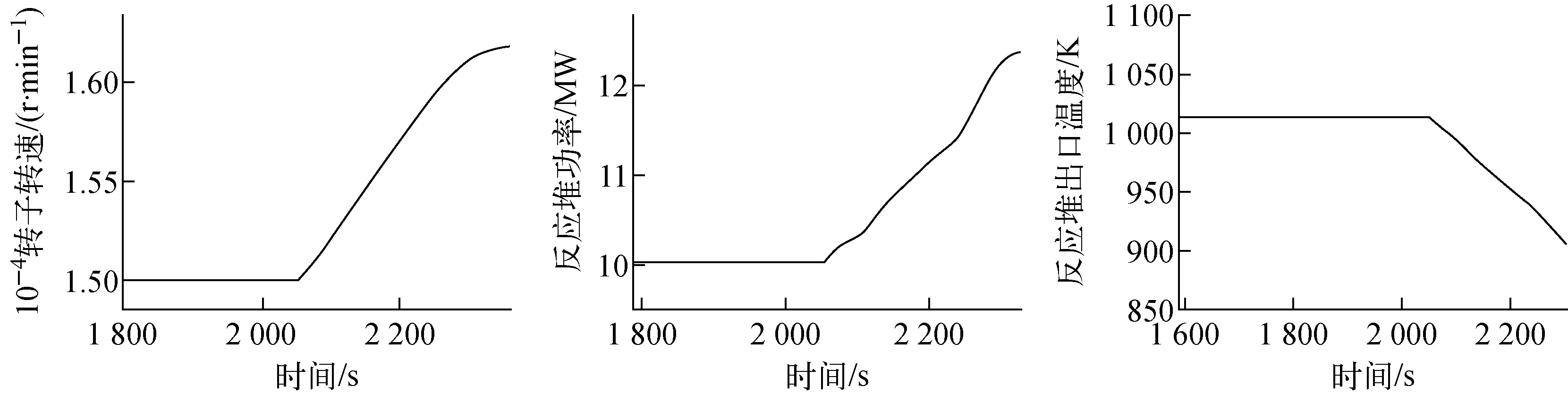
图6 转子转速、反应堆功率、反应堆出口温度曲线

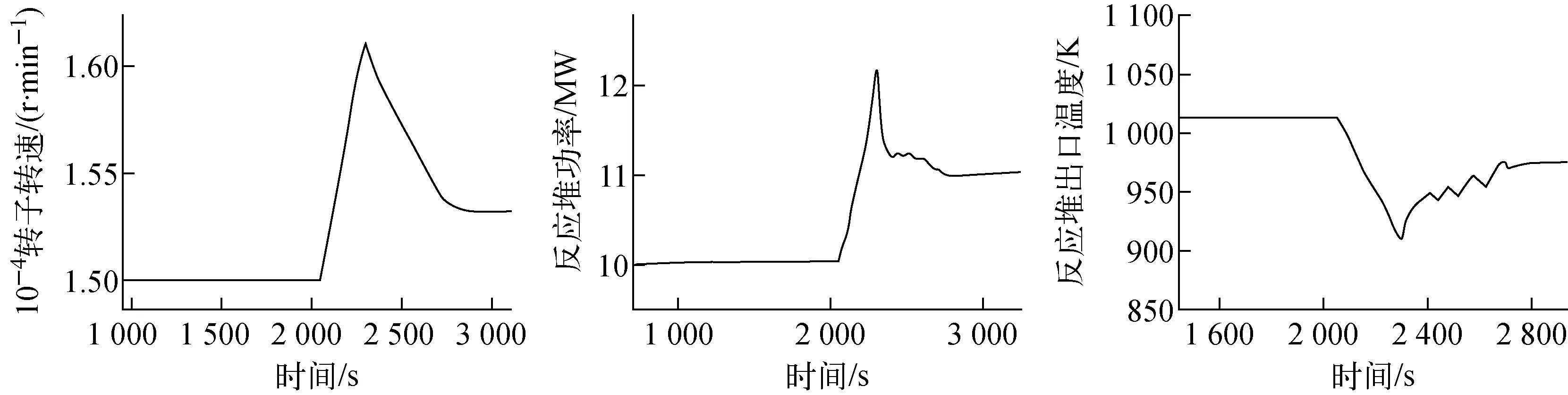
图7 加入转速控制后转子转速、反应堆功率、反应堆出口温度曲线

3 结论

本文基于模块化建模思想，建立了直接布雷顿循环反应堆系统分析程序，并针对典型稳态与瞬态工况条件下系统的动态特性进行了模拟仿真，主要得到以下结论：

1) 系统分析程序稳态仿真精度较高，关键设备参数仿真值与设计值相对误差不超过6.38%；

2) 各子模块耦合性能较好，能实时反映变工况下系统主要设备相关参数的变化趋势；

3) 系统具有一定的自稳自调能力，与小型布雷顿循环反应堆系统的固有安全性吻合较好；

4) 针对气轮机组甩负荷这种极限工况，在引入控制模块后，系统能在安全范围内运行，并验证了引入控制的必要性。

综上所述，本文开发的小型系统分析程序模块化程度高、计算速度快，为系统运行提供分析与变工况特性预测，并为直接布雷顿循环气冷反应堆系统的分析和优化提供技术支撑。