基于零和博弈的级联非线性系统的跟踪控制
杨雪静,李庆奎,易军凯
(北京信息科技大学 自动化学院,北京 100192)
0 引言
近年来,非线性系统的跟踪问题和最优控制问题作为控制理论的研究热点得到研究者的广泛关注[1]。非线性系统的跟踪问题主要有状态跟踪期望轨迹和输出跟踪期望轨迹两种;而最优控制就是在保证系统稳定的前提下找到一个控制策略,使得所定义的性能指标最小[2]。目前为止虽然对非线性系统的输出跟踪问题的研究成果已有很多[3],但是对最优追踪轨迹的研究大多是针对仿射非线性系统,而级联非线性系统模型在控制领域广泛存在,如:供应链、多智能体等,研究级联非线性系统的输出以最优方式跟踪期望轨迹有重要意义。
对于存在不确定干扰的级联非线性系统的最优跟踪控制,H∞控制提供了一个有力的工具减少干扰的影响[4]。根据博弈论的思想,普通H∞控制器的设计可视为控制和干扰的博弈,即控制器在最坏干扰下最小化性能指标达到最优控制。非线性系统博弈产生的HJI(Hamilton-Jacobi-Isaacs)方程是非线性偏微分方程,几乎不可能直接求解。ADP(adaptive dynamic programming)技术将最优控制、自适应控制和强化学习理论融合,利用函数近似结构估计值函数,近似求解HJI方程[5];利用函数近似结构更新值函数、控制策略和干扰策略,用神经网络形式表示为评价神经网络、控制神经网络和干扰神经网络。需要注意的是,ADP 技术普遍适用于仿射非线性系统[6],并不直接适用于级联非线性系统。为了得到级联非线性系统的最优跟踪控制,Zargarzadeh等[7]引入了自适应反推技术,基于状态反馈和输出反馈设计了没有干扰且系统内部动态未知时非线性连续时间系统的控制器,使系统输出以最优方式跟踪期望轨迹。Vamvoudakis等[8]提出了同步零和博弈策略迭代方法,即评价神经网络、控制神经网络和干扰神经网络的同时更新。本文与已有文献对级联非线性系统最优跟踪控制的研究不同,在本文中将干扰考虑在内,同步构建了评价网络、控制网络和干扰网络,采用反推技术和同步零和博弈策略迭代结合的方法设计了级联非线性系统的最优跟踪控制器。
1 问题描述与建模
考虑如下一类带有不确定干扰的级联非线性系统
(1)
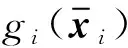
本文的控制目标是设计一个控制器u,使系统输出y以最优方式跟踪期望轨迹yd,并保证由式(1)给出的闭环系统中的所有信号有界。
2 前馈控制器设计
利用反推方法设计前馈控制器,将级联系统的跟踪问题转化为仿射跟踪误差系统的最优调节问题。反推设计过程描述如下:
步骤1系统(1)误差的一阶动态可以写为:
g1(x1)(x2-x2d)+k1(x1)d1=h1(e1)+f1(x1d)+
(2)

(3)
(4)
步骤i(2≤i≤n-1) 系统(1)误差的i阶动态可以写为
(5)
(6)
(7)
步骤n系统(1)误差的n阶动态可以写为
(8)
(9)
(10)
式(10)可写为
(11)
整个控制方案设计为U=Ua+U*。观察式(11)可知,要保证闭环系统的稳定性,不但要考虑前馈控制器的设计,还要考虑由最优反馈控制和干扰组成的微分博弈去镇定下列仿射形式的系统:
(12)
由最优反馈控制和干扰组成的微分博弈旨在镇定系统(12)且保证闭环系统中的所有信号有界。
3 基于ADP博弈的控制器设计
3.1 两人零和微分博弈问题
系统(12)可由式(13)描述:
(13)
式中:
X=[x1,x2,…,xn]T
H∞控制就是找到一个控制策略使得如下性能指标:
(14)
对所有的d∈L2[0,∞)和E(0)=0都是非正的。式中:Q(E)≥0是一个罚函数;R=RT>0;当γ≥γ*≥0,有控制策略存在时,就称系统具有L2增益小于等于γ,γ*是该问题有解的最小值。
最优反馈控制和干扰博弈的目标是找到零和博弈的纳什均衡点(U*,d*),在此情形下,由式(15)所示的值函数是最优反馈控制U*所能得到的最小值以及干扰d*所能得到的最大值。
(15)
将具有相关容许控制U和干扰d的Hamiltonian 函数定义为
(16)
(17)
当纳什均衡条件式(18)成立时,
(18)
两方零和博弈有唯一解,即存在鞍点(U*,d*):
(19)
将式(19)代入式(16),得HJI方程为
V*(0)=0
(20)
为了得到式(19)的鞍点解,必须求解式(20)的HJI方程。HJI方程是一个偏微分方程,用解析法很难得到。因此,本文采用ADP方法求解。
3.2 基于ADP的策略迭代算法
本文采用基于ADP的策略迭代算法,在迭代过程中利用ADP使用3个神经网络(评价网络、控制网络和干扰网络)分别近似值函数、控制策略和干扰策略。应用ADP求解HJI方程之前,引入下面的引理。

(21)
那么下面的关系成立:
(22)
假设闭环动态系统以系统状态函数为界:
(23)
根据Weierstrass高阶近似定理,存在完全独立的基础集φi(E),使得值函数V(E)及其梯度一致近似,用神经网络表示为
(24)
(25)
式中:Wc∈L(L是神经元数)和σ(E)∈L(σ(E)=[φ1(E),φ2(E),…,φL(E)]T)分别表示评价网络的理想权值和激活函数;εc(E)为神经网络近似误差。当L→∞时,εc(E)→0。
将式(25)代入式(16), Hamiltonian函数可化为
(H(E)+G(X)U+K(X)d)+εH=0
(26)
式中残差为
(27)
将式(25)代入式(19),鞍点解(U*,d*)可写为
(28)
HJI方程为
(29)
值函数近似产生的残差εHJI为
(30)

(31)
Hamiltonian函数为
(32)
(33)
(34)
权值估计误差为
(35)
根据式(29)、式(32)和式(34),得到评价网络的估计误差动态为
(36)
利用最小二乘法,得到式(26)的解为Wc,控制策略和干扰策略分别为
(37)
(38)

(39)
(40)
控制网络估计误差和干扰网络估计误差为
(41)
(42)


(43)
控制网络的调优律设计为
(44)
干扰网络的调优律设计为
(45)
式中:

4 稳定性分析
根据定理1中设计的评价网络、控制网络和干扰网络的调优规律,基于Lyapunov函数证明了通过参数的调整可以保证3个神经网络权值的收敛性和闭环系统的稳定性。
选择Lyapunov函数为
(46)
对t求导可得
(47)
将式(11)代入,得到
(48)
将评价网络的参数误差式(35)及其调优律式(43)和控制网络的调优律式(44)、干扰网络的调优律式(45)结合,得到
(49)
将式(49)和评价网络误差式(35)、控制网络误差式(41)及干扰网络误差式(42)代入,得到
(50)
将式(50)写为式(51),得到定理1中控制网络和干扰网络的调优律为
(51)
注意到
(52)
将控制网络调优律式(44)、干扰网络调优律式(45)和式(52)代入式(51),得
(53)
(54)
式中:T和M分别如式(55)和式(60)所示。
(55)
选择参数F1、F2、F3和F4使得M是正定矩阵。由式(54)可得
(56)
(57)
式中λmin(M)为M的最小特征值。
根据Young’s不等式和式(23),得到
(58)
(59)
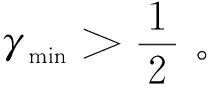
进而,式(59)可写为
(60)
(61)
或
(62)
或
(63)
5 数值仿真
为了验证本文所提方法的有效性及输出跟踪效果,利用Matlab软件进行了仿真研究。用于仿真的非线性系统模型为
(64)

在反推技术和博弈理论结合下,系统输出y(t)跟踪期望轨迹yd(t)的轨迹和跟踪误差y(t)-yd(t)分别如图1和图2所示。系统的控制输入轨迹和干扰输入轨迹分别如图3和图4所示。评价网络权值的变化如图5所示。
当仅用反推方法设计非线性系统式(64)的控制器时,系统输出y(t)跟踪期望轨迹yd(t)的轨迹和跟踪误差y(t)-yd(t)分别如图6和图7所示。系统的控制输入轨迹和干扰输入轨迹分别如图8和图9所示。
从图1和图6可以看出,在本文所提的反推技术和博弈理论结合下设计的控制器的跟踪效果更好。从图2和图7可以看出,在本文所提方法下系统的跟踪误差更小。从图8和图9可以看出干扰不能被由反推方法设计的控制器很好地抑制,而从图3和图4可以看出在本文所提方法下控制和干扰相互抑制,最终使得系统稳定。由此可见,在本文所提方法下设计的控制器,在系统稳定的同时系统输出跟踪期望轨迹的误差更小,跟踪效果更好。
6 结束语
对于一类有不确定干扰的级联非线性系统的输出跟踪控制问题,与以往方法不同,在本文中将控制和干扰视为零和博弈的双方,在跟踪过程中将跟踪轨迹的最优性考虑在内,利用反推方法将严格反馈系统转化成仿射非线性系统,然后使用ADP技术实时在线同步更新评价网络、控制网络和干扰网络的权值,得到了相应HJI方程的纳什均衡解。仿真结果证明了本文所提方法的有效性。在实际的工程领域中,系统的状态函数不是完全可知的,将本文所提方法应用于状态函数未知的级联非线性系统是进一步研究的方向。

