数控机床热误差预测的PSO-SVM模型
张 腰,杨庆东
(北京信息科技大学 机电工程学院,北京 100192)
0 引言
在数控机床加工系统的各类误差中,几何误差和热误差占数控机床加工系统总误差的40%~70%[1-2]。而主轴热误差是机床热误差中非常重要的一项。为减少主轴热误差的影响,需要对其进行溯源、分析与补偿,建立一个高精度的主轴热误差模型[3]。
国内外专家学者对此作了大量研究。王舒阳等[3]利用BP 神经网络的非线性函数拟合建模,但是该算法较为复杂,收敛速度慢,易陷入局部极值点,通用性欠佳;李泳耀等[4]-提出了基于最小二乘法支持向量机进行数控机床建模的预测方法,虽然该模型能够准确地预测热误差,但是训练需要大量的样本,过程计算复杂,训练时间长;林伟青等[5]提出了基于RBF(radial basis function)神经网络算法热误差模型,虽然与OLS(ordinary least square)回归模型相比,预测精度更好,但是模型训练样本多,复杂程度大,运算量大,调整权值过程中易出现病态;杜正春等[6]提出了基于模糊神经网络进行数控机床建模的预测方法,虽然能够准确预测热误差,但是该算法模型训练时间长,且收敛速度较慢。
本文采用粒子群算法优化支持向量机,建立PSO-SVM模型对数控机床热误差进行预测。粒子群算法能够避免陷入局部优化,更好地寻找支持向量机的参数C和g,优化热误差预测结果。PSO-SVM预测模型应用,为数控机床热误差建模预测提供了参考。
1 预测方案
1.1 支持向量机回归算法
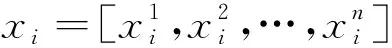
f(x)=〈w·φ(x)〉+b
(1)
式中:w∈Rn为权值;b∈R为阈值;φ为将Rn空间的输入数据映射到高维空间的映射函数,设算法函数为
(2)
通过寻找最优w、b在公式中固定不变的情况下最小化置信范围,得到的最优化问题为
(3)
(4)
利用拉格朗日乘子法求解凸二次规划问题,所得结果为
(5)
通过学习重新定义SVM函数为
(6)
式中:b为变换前阈值;K(xi,x)为支持向量机核函数。
高斯径向基核函数、多项式核函数、高斯核函数三个函数中,由于高斯径向基核函数只有一个变量需确定,以其构造的SVM训练参数相对较少,较易确定参数,因而本文采用的是高斯径向基函数:
(9)
1.2 粒子群优化算法
粒子群优化算法(particle swarm optimization,PSO)是群体智能的优化算法,该算法是通过粒子在解空间追随最优的例子进行搜索[8]。假设在数控机床热误差的一个L维空间中搜索由n个粒子组成的群体,设第i个粒子的位置为xt=(x1,x2,…,xn),速度为vt=(v1,v2,…,vn),则第i个粒子在解空间的速度和位置的关系变化为
(10)
式中:t为进化代数;w为惯性权重;rand( )为在区间[0,1]中分布均匀的任意数;pbj为当前粒子本身飞行过的最好位置;gbj为粒子所对应的整个种群的最好位置;c1和c2为学习因子。
2 PSO-SVM预测模型
首先将支持向量机的误差惩罚因子C和核函数g设为相应的位置向量X。设置参数C和g的范围分别为0.1~100 和0.01~2000[10]。具体实现步骤如下:
1)数据预处理。选取测量数据中的一组数据,将其归一化到[0,1]范围内:
2)初始化粒子群。设置参数c1=1.5,c2=1.7,w=0.4~0.9,种群最大数量为20,终止代数数量为200,随机产生粒子的初始位置和初始速度。
3)利用PSO算法对SVM算法中惩罚系数C和核函数参数g进行寻优,寻优过程如图1所示。
4)建立PSO-SVM模型。确定支持向量机回归机中的惩罚系数C和核函数参数g后,将最佳参数输入到模型中,在训练集上训练PSO-SVM模型。
5)数控机床主轴热变形预测。利用训练后的模型在测试集上测试模型回归效果,预测主轴热变形。
3 模型训练及结果分析
3.1 热误差数据采集
选取某立式加工中心进行热误差测量实验。本文只对数控机床部分发热部件进行实验分析和研究。根据机床热源的分布,将温度传感器布置在数控机床前轴承、后轴承、室温等几个温度点,S1~S5电涡流位移传感器分别测量X、Y、Z方向热误差变形量,电涡流位移传感器安装位置如图2所示。
在测量温度和热变形过程中,数控机床的主轴以3000 r/min的转速连续运行,当热变形和各个关键温度点变化微小时停机。在机床运转过程中,实时采集各关键温度测点温度和热误差,所测得的热漂移误差如图3所示。
从图3可以看到,随着机床的运转时间增加,机床关键点温度的变化是先逐渐增大,然后趋于变化微小,X、Y、Z轴热漂移误差先逐渐变大后变化微小,对应的热变形变化如图4、图5所示。
由图4和图5可知:在 0~200 min 温度上升期间内,数控立式加工中心X、Y、Z轴热误差和主轴热偏差随着温升而逐渐增大,当数控机床运行到200 min 以后,热误差变化量、主轴热偏差误差和各个温度关键点的温度值仅有微小的变化,数控机床基本达到热平衡状态。
3.2 数控机床热误差模型预测与对比分析
将PSO算法寻优得到的最优误差惩罚因子C和核函数g代入SVM模型可得到数控机床热误差变化模型。图6为未经PSO优化的SVM模型预测值与误差值,图7为经过PSO优化的SVM模型预测值与误差值。
由图6、图7可以看到2种算法模型都可以预测热误差变化,但PSO-SVM算法模型能够较准确地拟合出实际主轴热变形曲线的变化,其预测误差小于SVM模型算法的预测误差,PSO-SVM 预测精度更好一些。
为再验证PSO-SVM建模预测方法的可行性与准确性,对Z轴热误差数据进行分析如图8所示。
图中深色线为粒子群算法优化之后的误差曲线,浅色线为未经粒子群算法优化的误差曲线。可以看出:SVM预测模型在Z方向最大预测误差为6.02 μm,而PSO-SVM预测模型在Z方向最大预测误差为2.56 μm,PSO-SVM预测误差比未经粒子群算法优化的误差值更小,误差值波动较小,热误差预测精度较高。
4 结束语
为了提高数控机床热误差预测模型的精度,本文提出了一种PSO-SVM的算法模型,可以避免SVM陷入局部优化、收敛速度慢等不足。在样本数量较少的情况下,选取PSO-SVM模型进行数控机床主轴热变形的预测,PSO-SVM预测模型能够快速且准确地找到SVM 中各参数的最优值,具有较好的泛化能力和较高的精度。
将PSO-SVM模型用于对数控机床主轴热变形进行预测,并与SVM预测模型进行对比,结果表明PSO-SVM主轴热变形预测模型效果优于SVM预测算法,热误差预测精度较高且训练时间短,为数控机床热误差建模预测提供了参考。

