基于主成分回归分析的颜色与物质浓度辨识研究
王 军
(安徽财贸职业学院,安徽 合肥 230601)
检测物质浓度的方法之一是把需要待测的物质配置成溶液后滴在特定的白色试纸表面,待其充分反应后,将有颜色试纸与一个标准比色卡进行对比,即可确定待测物质的浓度档位,简称为比色法.其方法操作方便,设备简单,且对观察颜色的灵敏度较高,不同物质在不同的浓度下所对应的颜色度数也不尽相同,同时每个人对颜色存在敏感度差异和观测误差,使其对物质浓度的精准度也造成一定的误差,从而对相关实验的进程和结果造成很大影响.本文主要依据2017年全国大学生数学建模竞赛C题数据,在回归分析的基础上,建立了以RGB(红绿蓝)、H(色调)和S(饱和度)的读数为自变量,物质浓度为因变量的最小二乘法回归模型,得到了物质浓度与颜色读数之间的相关关系,建立了F检验和灰色关联分析法为准则的评价数据优劣的模型,并且对相关数据进行多重共线性诊断,得到了变量间存在显著的复共线性,构建主成分回归分析模型,得到较于一般最小二乘法回归方程更小误差的主成分回归方程,并给出了模型的误差分析.
1 颜色读数与物质浓度辨识分析
经过对5组数据进行处理发现,颜色读数在不同的水溶液浓度下具有一定的相关关系.初步判断组胺、溴酸钾、工业碱、硫酸铝钾的溶液浓度都随着颜色读数变化而变化,而奶中尿素浓度随颜色读数的变化波动性比较大.从数据中可以得到颜色读数在不同的水溶液浓度下具有一定的相关线性关系.在进行回归分析时,我们将所有的颜色读数作为自变量,物质浓度作为因变量,再进行多元线性回归分析,从而得到回归系数从而反映对应自变量的重要程度,所以我们将R,G,B,H,S作为函数的自变量X1,X2,X3,X4,X5,物质浓度为因变量Y,假设五元回归线性函数为:Y=β0+β1X1+β2X2+β3X3+β4X4+β5X5
根据数据,得到组胺、溴酸钾、工业碱、硫酸铝钾、奶中尿素的回归方程的回归系数和相关系数:
组胺:Y=-212.765+2.855X1-4.487X2+2.321X3+4.593X4+1.142X5
溴酸钾:Y=1449.592-12.588X1+4.867X2-1.277X3-7.094X4-6.347X5
工业碱:Y=261.65+0.164X1-1.398X2-0.313X3-0.131X4-0.880X5
硫酸铝钾:Y=17.537+0.053X1-0.018X2-0.102X3-0.134X4-0.020X5
奶中尿素:Y=12221.20+280.11X1+495.16X2-811.29X3-365.93X4+251.10X5

表1 不同物质的相关系数
表1中组胺、溴酸钾、奶中尿酸的相关系数都大于0.94,说明这三种物质浓度和颜色读数的关系呈高度相关,工业碱、硫酸铝钾的相关系数介于0.5到0.8之间,呈显著相关关系,所以通过数据分析可以确定颜色读数和物质浓度之间的关系.
1.1 数据评价准则
在对5种物质回归分析的过程中,我们准备用F检验和灰色关联度分析来分析这5种物质数据的优劣程度.
准则1(F检验):
利用SPSS软件对数据进行回归分析中得到5种物质F检验资料见表2

表2 五种物质的F检验资料
从而得到这5种数据的优劣程度,顺序如下:组胺>溴酸钾>奶中尿素>硫酸铝钾>工业碱.
准则2(灰色关联度分析法):
为了更加精准评价数据的优劣,引入SPSS软件处理所得的多个指标采用灰色关联来评价数据的优劣.通过SPSS软件对数据进行回归分析中得到5种物质统计资料见表3:
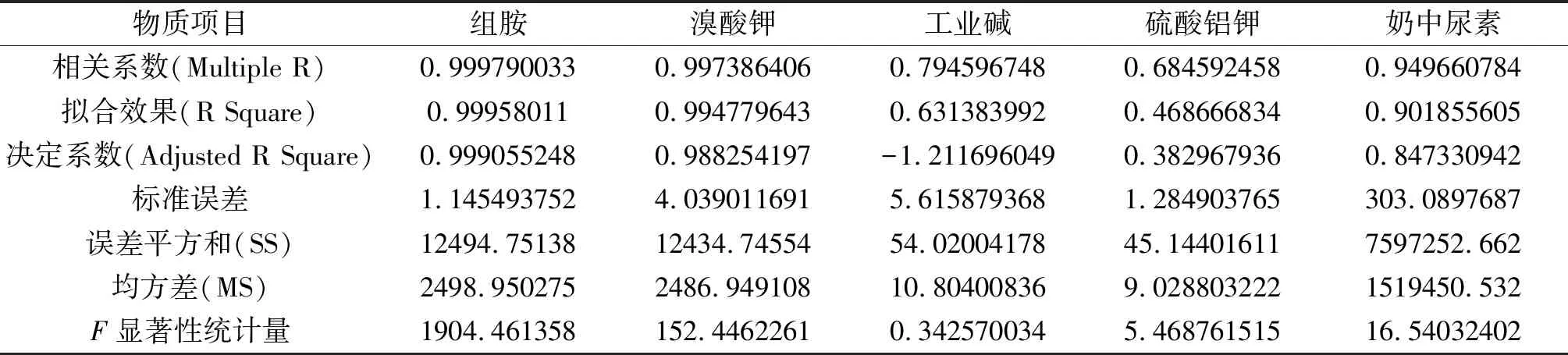
表3 5种物质分析统计表
针对于多元回归分析中得到的数据,拟采用灰色关联度分析法对各个指标数值进行分析,具体步骤如下:把5种物质作为评价对象,相关系数、拟合效果、决定系数、标准误差、误差平方和、均方差和F显著性统计量为评价指标,计算灰色关联系数:
计算灰色加权关系度.灰色加权关系度的计算公式为
运用Matlab软件处理,得到组胺、溴酸钾、工业碱、硫酸铝钾、奶中尿素的灰色关联度分别为0.6192、0.5222、0.5751、0.5346、0.5938,可以得到这5种数据的优劣程度,顺序如下组胺>奶中尿素>工业碱>硫酸铝钾>溴酸钾.
1.2 二氧化硫的主成分回归分析
以二氧化硫为例,对数据进行预处理,得到二氧化硫浓度随颜色变化可能呈一定线性关系.
1.2.1 多重共线性的诊断
为了建立较为稳定的线性回归模型,对数据进行多重共线性的诊断,应用SPSS 进行多重共线性诊断,得到回归系数与共线性诊断如表4和表5:

表4 相关系数矩阵

表5 共线性诊断统计表
对数据进行复共线性判断:
(1)特征分析法
原自变量的相关系数,相关阵R的特征值为λ1=0.191,λ2=0,λ3=0.00003302,λ4=0.00001284,λ5=0.00000606,λ2,λ3,λ4,λ5均<0.01,可认为变量间存在严重复共线性.
(2)条件数法
表6中条件数介于400~1000之间,显然变量间存在显著的复共线性.
1.2.2 模型的建立与求解
设二氧化硫的颜色指标B、G、R、H、S分别为X1,X2,X3,X4,X5,浓度为Y. 首先将因变量Y的标准化为和5个标化自变量,分别为:
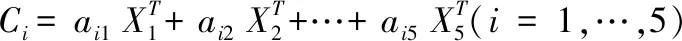
然后计算相关系数阵的5个特征值和各个自变量的累积贡献率,通过分析可以看出,前三个变量的累积贡献率达到0.99495,于是略去后两个变量.最后用matlab软件作主成分回归分析,得到回归方程
化成标准化的回归方程
恢复到原始的自变量,得到主成分回归方程
剩余标准差为S=22.8457,可见主成分回归方程较于一般的最小二乘法的回归方程具有更小的误差.
1.2.3 误差分析
2 评价与改进
针对颜色读数与物质浓度的关系问题,本文通过对数据的回归分析和处理,建立了主成分回归模型,但变量间的多重共线性增加了解决问题的难度,因此本文通过降维的方法,降低了问题的复杂性.在模型的改进中我们可以考虑主成分选取贡献率一定要高,其次选取的主成分一定要能够反映问题的实际信息,主成分的个数一定要小于原始个数,这些情况都会影响模型的准确性,这也是研究改进方向.

