不同养护温度下蒸养混凝土的冲击性能

谢友均， 王 猛， 马昆林， 龙广成

(中南大学 土木工程学院， 湖南 长沙 410075)

混凝土作为最大宗基础性工程材料，在交通基础设施如公路、机场、高铁轨道结构以及防护结构等工程中应用广泛，在其服役过程中不仅承受静态荷载，也需要承受机械冲击等动态荷载.因此，掌握混凝土材料在冲击荷载作用下的力学特性具有重要实践意义.研究者们已采用了多种模拟试验方法对混凝土动态力学性能进行研究，其中分离式霍普金森压杆(SHPB)试验方法是研究混凝土冲击性能的常用方法之一.已有不少公开报道的研究成果涉及冲击荷载作用下混凝土动态受压性能[1-3]和动态拉伸性能[4-8]等的研究，并建立了相应混凝土的动态力学损伤本构模型[9-20].Li等[21]和王道荣等[22]还总结了影响混凝土动态力学性能的主要因素.

然而，这些研究主要针对普通混凝土，有关蒸养混凝土冲击性能的研究还非常有限.蒸养混凝土广泛用于预制构件生产，如中国高速铁路简支梁、轨枕、轨道板等.这些预制构件除承受自重荷载和上部荷载等静态荷载作用外，还承受列车高速运行时的冲击动态荷载作用.贺智敏[23]采用落锤试验研究了蒸养混凝土的冲击韧性，发现相较于普通混凝土，在较高温度下养护得到的蒸养混凝土冲击韧性更低，脆性更大.这说明蒸汽养护条件对混凝土力学性能有较大影响.因此，有必要更全面地了解和掌握蒸养混凝土在冲击等动态荷载作用下的力学特性.

鉴于此，本文采用SHPB试验方法，以中国高速铁路预制轨道板用典型C60蒸养混凝土为研究对象，研究蒸养混凝土在冲击荷载下的力学特性及其应变率效应，分析养护温度(20～80℃)对其冲击性能的影响规律，为优化蒸养混凝土的蒸养制度以及掌握蒸养混凝土(预制构件)的服役性能提供支持.

1 试验

1.1 原材料及配合比

水泥(C)为中国建筑材料研究总院生产的 P.I 42.5 基准水泥.矿物掺和料采用粉煤灰(FA)和矿渣(GGBS)，粉煤灰为湖南省湘潭电厂生产的Ⅰ级粉煤灰，比表面积为410m2/kg；矿渣为萍乡钢铁厂新材料有限公司生产的S95级矿渣.水泥、粉煤灰和矿渣的化学组成(1)文中涉及的组成、水胶比等均为质量分数或质量比.如表1所示.粗骨料(CA)为粒径5～ 20mm 的连续级配石灰石碎石，其中粒径5～ 10mm 碎石占40%，粒径10～20mm碎石占60%.细骨料为湘江河砂(S)，级配符合Ⅱ区要求，细度模数为2.88.减水剂采用聚羧酸减水剂(SP)，减水率大于20%.拌和水(W)采用自来水.混凝土设计强度为C60，水胶比mw/mb为0.30，配合比如表2所示.

表1 水泥、粉煤灰及矿渣的化学组成

Table 1 Chemical compositions of cement,FA and GGBS

w/%

表2 C60混凝土配合比Table 2 Mix proportion of C60 concretes kg/m3

1.2 试件成型及养护方案

采用强制式搅拌机来拌和混合料.将粗、细骨料和胶凝材料按顺序加入搅拌机中，干拌均匀后缓慢加入水和减水剂，全部加料时间不超过2min.待水全部加入后，继续搅拌2min.各拌和物坍落度保持在50～80mm.

将拌和物浇筑于直径和高度均为75mm的钢质试模和100mm×100mm×100mm的塑料试模中，分别用于制备SHPB测试和抗压强度测试用试件.浇筑后放在振动台上振动成型.

对浇筑成型后的试件分别进行标准养护(标养)和蒸汽养护(蒸养).标养温度为(20±2)℃，相对湿度大于等于95%，试件成型1d后拆模，养护至28d.对于蒸养试件，试件浇筑成型后带模放入标准养护室中静停 2h，随后放入蒸汽养护箱内进行蒸养，升温速率保持在 15～ 20℃/h，恒温时间为8h，养护温度分别取45、60、80℃，降温速率为15～20℃/h，试件蒸养结束后脱模，放入标准养护室中继续养护至28d龄期.

1.3 测试方法

1.3.1抗压强度

混凝土抗压强度的测试按照GB/T 50081—2002《普通混凝土力学性能试验方法标准》进行，不同养护温度下混凝土圆柱体试件28d静态抗压强度如表3所示.

表3 不同养护温度下混凝土圆柱体试件28d静态抗压强度Table 3 28d static compressive strength of cylinder concrete specimens under different curing temperatures

1.3.2SHPB测试

采用φ75杆径的SHPB试验测试系统，该系统主要由发射腔、冲头、入射杆、透射杆、能量吸收杆和数据采集系统组成.测试系统为CS-10型超动态应变仪，具有校准和自动平衡功能.按SHPB测试要求将试件加工打磨平整，厚度控制在75mm左右，端面不平整度小于0.02mm.具体测试与计算方法参见文献[24-26].

2 结果与讨论

2.1 试件破坏形态

混凝土是多物相的多孔性复合材料，其中骨料与水泥石界面和水泥石内部均存在较多的初始缺陷，如裂缝、孔隙等，这些初始缺陷是混凝土的薄弱部位，在荷载作用下，这些部位首先扩展，随着荷载的增大，裂纹逐渐扩展并连通，形成贯通的主裂纹.混凝土的受压破坏是其内部微裂纹形成、不断扩展直至连通破坏的过程.图1给出了不同应变率下 20℃ 标养和60℃蒸养混凝土的受压破坏形式.

图1 不同应变率下20℃标养和60℃蒸养混凝土的受压破坏形式Fig.1 Compressive failure modes of 20℃ standard cured and 60℃ steam cured concretes under different strain rates

由图1可知：混凝土试件在准静态加载时的受压破坏形式为剪切破坏；在低应变率(10-3s-1)下的受压破坏形式兼具剪切破坏和劈裂破坏特征，试件受压面上裂纹数量明显增加，骨料破坏现象更为明显，且呈现出劈裂破坏的形式，说明在低应变率范围内，随着加载速率的提高，裂纹不完全是沿着试件内部的薄弱部位产生、扩展并连通，而是部分裂纹直接穿过骨料形成多条主裂纹贯穿整个试件；值得注意的是，在SHPB试验的高应变率条件下，标养和蒸养混凝土的破坏形式与准静态、低应变速率加载条件下有显著不同，混凝土试件在冲击荷载作用下瞬间被破碎成小碎块，且随着应变率的进一步提高，混凝土试件的破碎程度更为严重，如 图1(c)、(d)所示，这主要是由于当应变率较高时，混凝土内的原始缺陷来不及扩展，此时，混凝土吸收的能量主要以产生更多细小裂纹的方式被消耗，从而导致混凝土破损程度更大[27].

为了定量表征不同应变率下标养和蒸养混凝土试件的破碎程度，采用筛分试验对各破坏试验后粒径9.5～0.15mm的混凝土破碎颗粒进行分析[28]，按式(1)计算各混凝土试件破碎后的颗粒细度模数Mx，并用颗粒细度模数来定量表征破碎程度.

(1)

式中：A1～A7分别为9.5、4.75、2.36、1.18、0.63、0.3、0.15mm的累积筛余.

图2 混凝土破碎颗粒细度模数随应变率的变化Fig.2 Variation of fineness module of broken concrete particle with strain rate

由图2可知：随着应变率的增加，4种养护温度下混凝土破碎后的颗粒细度模数均显著下降，且颗粒细度模数与应变率之间呈现较为明显的线性关系，表明随着应变率的增加混凝土试件的破碎程度明显增加，碎片的平均尺寸明显降低，从大块的碎片向细小的碎片甚至粉末状态转变；在相同应变率下，混凝土破碎后的颗粒细度模数随养护温度升高而明显增大，说明随着养护温度的升高，混凝土试件的破碎程度和破坏时所释放的能量明显降低，这是由于随着养护温度的升高，其对混凝土产生的热损伤增大[23]，导致混凝土内部初始缺陷增多从而耗散了一部分能量，因此只需更少的裂纹扩展就可消耗剩余的能量.

2.2 应力-应变特性及其应变率效应

基于SHPB试验测得28d龄期时4种养护温度下的混凝土在不同应变率下的压应力-应变(σ-ε)曲线如图3所示.由图3可知，与静态抗压强度(见表3)相比，各混凝土在冲击荷载作用下的峰值应力σd显著提高，且随着应变率的增加而增大.这主要是因为：当应变率较低时，混凝土内裂纹有足够的时间进行扩展，其在外荷载作用下吸收的能量主要用于其内部原生缺陷的扩展与贯通，此时混凝土的破坏程度较小，抗压强度较低[29]；当应变率较高时，混凝土内的原始缺陷来不及扩展，其吸收的能量主要以产生更多细小裂纹的方式被消耗，又由于荷载作用时间极短，混凝土没有足够的时间来进行能量的耗散，只能通过增加应力的方式来抵消外部能量,因此在高应变率下，混凝土的破坏程度较大，抗压强度较高[30].同时，混凝土试件的侧向惯性约束作用和端部摩擦作用也会使其在冲击荷载作用下的动态强度显著提高[31].有研究者提出，硬化水泥浆体黏弹性特性和裂纹扩展时变特性也是引起混凝土峰值应变产生应变率效应的重要原因[32-33].

由图3还可知，各混凝土试件峰值应力对应的应变(峰值应变)随着应变率的增加而呈降低趋势，这是由于随着应变率的增加，混凝土试件在外部冲击荷载作用下的变形没有充分的时间响应就被完全破坏，从而表现出更为显著的脆性破坏特征.

2.2.1峰值应力的应变率效应

对各混凝土试件峰值应力σd与应变率的关系进行作图，见图4.从图4可以看出，各养护温度下混凝土的峰值应力均随应变率增加而增大，且两者之间呈现较好的线性关系.为进一步建立混凝土峰值应力与应变率之间的数学关系，更好地描述冲击荷载作用下混凝土峰值应力随应变率和养护温度的变化规律，引入动态增长因子(DIF)，用于量化混凝土峰值应力的应变率效应[34-35]：

(2)

式中：σs为混凝土的静态峰值应力，MPa.

图5给出了各混凝土试件动态增长因子与应变率的关系.由图5可知，各试件DIF与应变率的对数之间均存在良好的线性关系，随着应变率对数的增加，试件DIF线性增大.

对图4、5中各混凝土试件峰值应力、DIF与应变率的关系进行拟合，结果见表4.由表4可知：随着养护温度的升高，拟合方程的斜率增大，即混凝土峰值应力和DIF随应变率(对数)增加的增长速率明显提高；20、45、60、80℃下DIF随应变率对数的增长速率分别为1.881、2.002、2.689、3.051，表明随着养护温度的升高，混凝土的应变率效应增强；当养护温度为20、45℃时，混凝土的峰值应力增长速率较为接近；当养护温度超过60℃时，混凝土峰值应力的增长速率更为明显，应变率效应显著提高，说明当养护温度超过60℃后，混凝土内部的初始缺陷增多，冲击荷载作用下的部分能量被这些初始缺陷吸收，从而使混凝土的峰值应力表现出较强的应变率效应.

图3 各混凝土试件的压应力-应变曲线Fig.3 Compressive stress-strain curves of concrete specimens under SHPB test

图4 各混凝土试件峰值应力与应变率的关系Fig.4 Relationship between peak stress of concretespecimens and strain rate

图5 各混凝土试件动态增长因子与应变率的关系Fig.5 Relationship between DIF of concretespecimens and strain rate

2.2.2峰值应变的应变率效应

对于混凝土峰值应变与应变率关系的研究，不同学者得到的结论并不一致[2,29,36-38]，这可能是由试验条件差异所致.在本文所测冲击荷载作用下，各混凝土试件峰值应变εp与应变率的关系如图6所示.由图6可见，总体上，各养护温度下混凝土的峰值应变随应变率增加而呈降低趋势，且两者呈现较好的线性关系.通常，在荷载作用下，混凝土峰值应变由2部分组成，即弹性应变和塑性应变，当应变率增加时，塑性应变减弱，导致混凝土峰值应变随应变率增加而显著降低[24,39].同时，在高应变率下，混凝土中裂纹的扩展速度随着应变率的增加而增加[38]，但是，裂纹的扩展速度远远小于混凝土中应力波的传播速度[40].因此，应变对于高速的应力波产生延迟响应现象，在给定应力下的应变随着应变率的增加而降低[41].

表4 各混凝土试件峰值应力、DIF与应变率的拟合方程Table 4 Fitting formulas for the relationship between peak stress，DIF of concrete specimens and strain rate

图6 各混凝土试件峰值应变与应变率的关系Fig.6 Relationship between peak strain of concrete specimens and strain rate

由图6还可知：养护温度对混凝土峰值应变的应变率效应影响较明显；相比于20℃，45℃和 60℃ 下混凝土在相同应变率下的峰值应变均较小；80℃养护下的混凝土在各应变率下的峰值应变则明显降低，这可能与较高养护温度下混凝土内物相与孔隙结构有关.养护温度提高，水化物相晶态化倾向增加，孔隙粗化更为显著，导致蒸养混凝土峰值应变降低，脆性增大[23].

3 考虑应变率的本构模型

3.1 本构模型的建立

不少学者基于Lemaitre的应变等价性假说和统计损伤理论，探讨了混凝土的动态损伤本构模型[1,18-19,24,26].本文也基于上述理论，建立考虑应变率效应的蒸养混凝土本构模型，将混凝土在变形破坏过程中的裂纹发展视为损伤的发展，并引入损伤变量D，建立带损伤变量的混凝土本构模型：

σ=E(1-D)ε

(3)

式中：E为混凝土弹性模量.

假定混凝土由无数个微元组成，在宏观上，微元足够小，微元破坏前为线弹性体，破坏后不再具有承载能力，各微元的损伤发展服从Weibull分布，损伤变量D的表达式为[26]：

(4)

式中：F0和m为与损伤分布相关的参数[25-26].

将式(4)代入式(3)即可得到考虑应变率效应(主要是参数F0，m)的混凝土损伤本构模型：

(5)

3.2 本构模型的验证

按式(5)对混凝土冲击荷载作用下实测的压应力-应变曲线(图3)进行拟合，相关系数R2如表5所示.由表5可见：各应变率下混凝土的应力-应变曲线拟合结果与试验结果吻合良好，相关系数均达0.83以上.说明双参数Weibull模型中的参数m和F0与混凝土受冲击荷载过程中的力学性能密切相关.参数m反映了混凝土的脆性(或延性)性质，而参数F0则与混凝土的峰值应变及m值相关，反映其损伤程度[1,26].当F0恒定时，m越大，混凝土脆性越大，而延性越小；当m恒定时，F0越低，表示混凝土损伤程度越大.

表5 各混凝土应力-应变曲线的拟合相关系数Table 5 Fitting correlation coefficient of stress-strain curve of concretes

图7给出了各混凝土模型参数m、F0与应变率的关系.从图7可看出：参数m、F0与应变率之间具有良好的线性相关性，这与文献[25-26]中的结果一致；养护温度对参数m的影响规律不明显；养护温度为80℃时，在各应变率下试件的F0值相对较低，表明80℃下混凝土内部损伤较大.

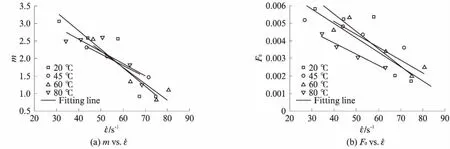
图7 各混凝土模型参数m、F0与应变率的关系Fig.7 Relationship between model parameters m,F0 of concretes and strain rate

当养护温度超过60℃时，混凝土峰值应力的应变率效应显著提高.当养护温度超过80℃时，混凝土在各应变率下的峰值应变和模型参数F0明显降低.这表明超过相应养护温度时，混凝土内部由于热损伤造成的初始缺陷明显增多.因此，为降低蒸汽养护制度造成的热伤损，建议蒸汽养护恒温段的温度不宜超过60℃.

4 结论

(1)采用蒸养混凝土破碎后的颗粒细度模数作为指标，可有效表征冲击荷载作用后蒸养混凝土的破碎程度.随着应变率的增加，混凝土破碎后的颗粒细度模数减小，破碎程度增加；随着养护温度的升高，蒸养混凝土的破碎程度降低.

(2)在冲击荷载作用下，随着应变率的增加，蒸养混凝土28d龄期时的峰值应力增大，峰值应变则降低；蒸养混凝土动态增长因子DIF与应变率的对数具有良好的线性相关性.

(3)随着养护温度的升高，蒸养混凝土28d龄期时的峰值应力降低，尤其是当养护温度超过60℃(如本试验80℃)后，混凝土峰值应力显著降低.较高的养护温度使蒸养混凝土表现出更强的应变率效应.

(4)本文建立的考虑应变率的蒸养混凝土本构模型拟合结果与试验结果吻合较好，模型参数m和F0随应变率增加均呈现较明显的线性下降趋势.

(5)综合考虑蒸养过程中的热损伤及其对蒸养混凝土冲击性能的影响，建议蒸汽养护最高温度不高于60℃.