变距螺旋管式油水分离器结构参数优化设计研究
王建国
(大庆油田有限责任公司第四采油厂,黑龙江 大庆 163000)
多相介质流动作为一种复杂的流体形态在化学工业、冶金工程及能源环保等诸多研究领域中都普遍存在[1-2],其中的螺旋管分离器是作为一种常见的典型分离设备一直备受关注,它不仅结构简易、分离效果显著,而且适应流量大等优点也使得其在多相分离的技术运用中日益凸现出来[3-5]。龚道童等[6]通过运用FLUENT软件开展了螺旋管内油水两相流动及离心分离情况的数值模拟,分析得出了不同流速与油水配比工况下的螺旋管内的油水组分、各相速度、相含率、各相流量等重要性能参数的变化。钟秋月[7]在结合管柱式气液旋流分离器(简称GLCC)[8]和液-固旋流器的基础上设计完成了可实现气液固三相分离的旋流分离器,并通过对其内部流场的模拟计算与实验研究获得了分离器的气体最佳操作范围与入口含液浓度对分离效率的影响规律。赵立新等[9]针对螺旋管分离器分别进行了无孔和开孔的流场模拟,并对回转半径与入口流量对流场分布和分离性能的影响开展分析,得出螺旋管开孔孔径尺寸对其分离效果也会产生一定的影响,且得到了该分离器的最佳回转半径。此后,又有学者[10-14]对螺旋管内不同介质相的流速、孔径、分离性能等多项参数进行了模拟研究与实验分析。
但上述研究大多集中于螺旋管分离器的结构及操作参数的优化模拟,而对其参数的优化方法研究鲜有报道,本文拟在借助FLUENT软件的基础上,采用正交实验的方法对一种新提出的变距螺旋管开展结构参数优化设计,并通过对数值模拟结果的对比分析,考察建立该变距螺旋管的最优结构参数尺寸,并以此为基础推广到其他螺旋分离器的参数优化中。
1 模型构建与网格划分
1.1 流体域模型
变距螺旋管的结构主要由入口管、溢流管与底流管等组成,其流体域模型原理如图1所示,油水混合液由入口进入螺旋管内,在螺旋管内形成旋转运动,在离心力作用下油相沿螺旋管内侧运动,水相在螺旋管边壁,油相沿出口管与螺旋管的连接管进入溢流出口管内,水相沿底流口排出,实现油水两相分离。其流体域模型的尺寸结构如图2所示,其中,入口管与底流管内径相等为S,溢流管内径为d,螺旋管总长为L,螺距为l,螺旋管锥角为β。

图1 变距螺旋管流体域的模型原理Fig.1 Model principle of variable pitch spiral tube fluid domain

图2 变距螺旋管流体域的模型尺寸Fig.2 Model size of variable pitch spiral tube fluid domain
1.2 网格划分
运用FLUENT前处理软件GAMBIT对上述螺旋管的流体域模型进行网格划分处理,由于四面体网格具有单元疏密程度较均匀,变形能力较强,跟随性较好等优点,所以本文选用四面体结构性网格对设计的变螺距螺旋管进行有限元网格划分。最终的网格划分结果如图3所示。变螺距螺旋管流体域模型的网格划分单元数为225 860,采用网格质量检测对流体域网格进行有效性检验结果显示网格有效率为100%。
2 介质物性参数及边界条件设置
数值模拟中采用油水两相为模拟介质,其中设定水相为连续相,密度为998.2 kg/m3,动力黏度为1.003×10-3Pa·s;设定油相为离散相,密度为889 kg/m3,动力黏度为1.06 Pa·s,油水界面张力取0.05 N/m;并定义该螺旋管入口边界条件为速度入口,其中分散相油滴与连续水相的速度值相同,且分散相油滴在入口界面处均匀分布;溢流与底流则均定义为自由出口;油相所占质量分数为3%,溢流口分流比为20%,入口速度设为6 m/s,壁面条件选择不可渗漏,无滑移固壁。通过采用有限体积法转化控制方程为可用数值方法求解的代数方程。此外,通过SMPLEC算法完成压力-速度耦合;并运用雷诺应力模型完成初始流场的计算,计算精度设置为10-5。
3 正交实验设计
本文采用正交试验设计对上述的变螺距螺旋管的结构参数完成优化设计,进而得到螺旋管的各项结构参数的最优数值,进而提高油水两相在螺旋管内的分离效率。该变距螺旋管结构参数较多,其中螺旋管锥角β、螺旋管圈数q和溢流管径d对螺旋管的油水分离效率影响较多,所以本设计在正交设计中仅对螺旋管锥角β、螺旋管圈数q和溢流管径d进行参数优化,检验上述不同参数的螺旋管对油水分离效率的影响以此来评价螺旋管的分离效率。 选取螺旋管锥角β取值范围为5°~15°,螺旋管圈数q取值范围为5~6,溢流管径d取值范围为50~70 mm。通过查阅正交表,最终选定本次正交试验选用L9(34)正交试验表,完成表1所示的表头设计。

图3 变距螺旋管流体域的网格划分Fig.3 Grid division of variable pitch spiral tube fluid domain

表1 螺旋管结构参数因素水平表Table 1 Table of factor levels of spiral tube structural parameters
4 正交结果分析
采用数值模拟方法按照变螺距螺旋管分离器的结构参数优选正交试验设计表,对不同试验设计组进行数值模拟,模拟时保障操作参数及介质物性参数不变,严格控制操作参数单一变量,同时为了降低数值模拟时产生的分析误差,每组试验进行两次同精度的数值模拟,并按照质量效率式(1)完成指标计算。
Ez=Mu/Mi
(1)
式中:Mu为溢流口中油的质量;Mi为入口中油的质量;Ez为质量效率。
得到9组不同匹配方案下的螺旋管油水两相分离效率,为了对正交实验结构进行系统分析,本文在直观分析方法的基础上,辅以方差检验的方法对上述正交试验所取得的数据进行讨论分析。
4.1 直观分析
采用数值模拟计算方法对设计的变距螺旋管结构参数的9组正交优化试验结果进行模拟,得到试验结果(表2)。试验分析指标为变距螺旋管的油水分离效率值。表中K1、K2、K3分别表示因素水平号为1、2、3时试的不同验指标总和,而k1、k2、k3则用以表示因素水平号分别为1、2、3时的不同试验结果平均值,极差R表示各个因素所在列上K的最大值与最小值之差。正交实验中极值最大列所对应的因素水平变化对试验指标结果影响最为显著,对于本次螺旋管正交优化设计而言三种因素对变距螺旋管油水分离效率影响显著性从高到低分别为螺旋管锥角β、螺旋管圈数q和溢流管径d,空列反应的极差是实验误差的大小。

表2 试验结果及分析表Table 2 Test results and analysis table
由于本设计的螺旋管采用油水两相的分离效率来评价,分离效率越高说明油水分离精度越好,即越接近结构参数最优结构,因此在选取k值较大者所对应的因素水平数作为单项最优采纳数,由表2可知对于因素A列其顺序为k1>k2>k3,因素B列k3>k2>k1,因素C列k2>k3>k1。由于正交试验直观分析表2中的k值对应的数据可直接反映出各因素的性能水平,对于因素A而言k1值最大,所以A1为因素A的最优方案,同理可以得出因素B的最优方案为B3,因素C的最优方案为C2,最终可确定出试验优化后的最佳方案为A1B3C2,即螺旋管锥角β为5°,螺旋管圈数q为7,溢流管径d为60 mm时,螺旋管油水分离效率最大,由于正交试验的极差值R可反应出各因素对试验指标的影响程度,极差值越大说明该因素对指标影响越显著,因此本次试验各因素对试验指标影响的主次顺序为A>B>C。
4.2 方差检验
为了评估正交试验的误差大小并精确的估计出各个素对试验结果的重要程度,进而开展显著性检验,且采用方差检验对结果验证。
4.2.1 自由度
正交试验中总平方和的总自由度计算公式为式(2)。
dfT=试验总次数-1=n-1
(2)
正交表任一列离差平方和所对应的自由度的计算公式为式(3)。
dfi=因素水平数-1=r-1
(3)
显然总自由度同时满足式(4)。

(4)
而误差的自由度按式(5)计算。
dfe=∑df空列
(5)
按照上述自由度计算方法可以得出,本次正交试验所涉及的自由度分别为dfT=8,dfA=dfB=dfC=2,dfe=2。
4.2.2 显著性检验
对本文正交试验结果显著性分析时,采用F检验方法,即可通过比较不同FA,FB,FC和临界F值的差值大小而计算获得不同因素的显著情况。假若FA>Fα(dfA,dfe),则说明因素A对试验指标存在明显的影响结果,通常情况下在进行显著性F检验时一般要完成α=0.01、α=0.05、α=0.10三个不同水平的显著性检验。在本次正交试验中根据F分布表,即F0.01(2,2)=99、F0.05(2,2)=19和F0.10(2,2)=9查得临界值,得出螺旋管各因素的显著性检验的方差分析结果,见表3。
因素C平均离差平方和小于误差项离差平方和,将因素C归入到误差项中。由上表中的显著性检验结果可以看出,上述各不同因素对本试验指标的主次影响顺序基本表示为因素A>因素B>因素C,即方差检验与直观分析所示结果相一致。
5 优化方案验证
为验证上述变距螺旋管结构参数中正交优化结果的准确性,从正交表中的9个试验组中按照油水分离效率从大到小的顺序随机选取两组试验开展流场分析,选取的试验组数分别为试验3#和试验7#,对上述试验所对应的螺旋管结构参数组合进行分离效率及油相分布对比,分析螺旋管内部油相分布特性,验证正交试验结果得出的关系。采用欧拉-欧拉方法进行数值模拟,得出试验3#和试验7#螺旋管内油相分布对比如图4所示。图4所示当混合相从入口进入螺旋管后,轻质油相往螺旋管内侧运移,且内侧油相体积分数远大于外侧油相体积分数。内侧的油相经过横管进入到溢流管中,在重力的作用下油相向上浮起流经到沉降罐中,水向下沉淀流出。图4从左至右分别是试验3#、试验7#,试验3#的油水分离效率明显大于试验7#,尤其是在螺旋管上半部分,试验3#的油相分布远远高于试验7#。
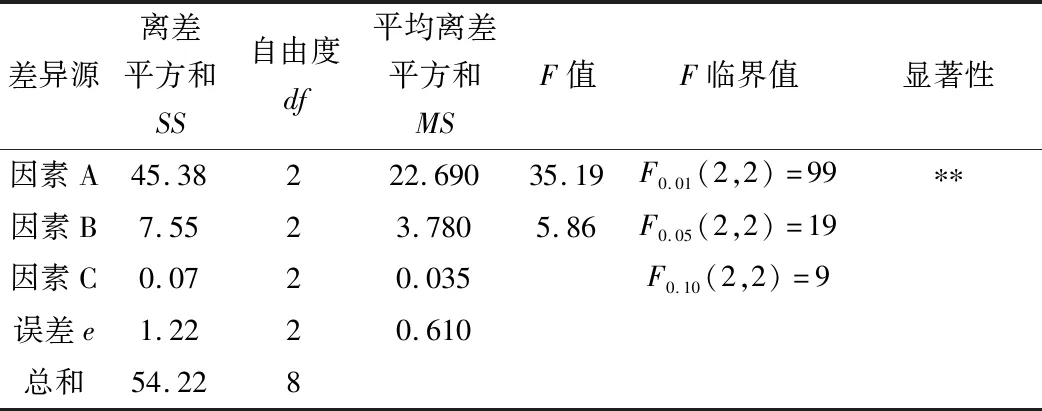
表3 方差分析表Table 3 Analysis table of variance
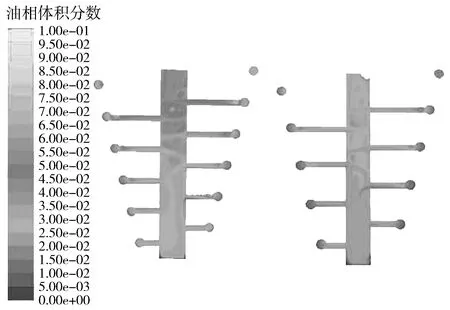
图4 试验3#和试验7#半剖油相分布云图Fig.4 3# and 7# test half profile oil phase distribution cloud diagram
图5所示为螺旋管流体域外观油相分布,螺旋管外侧为水相,内侧为油相。很明显地可以看出油水两相在螺旋管中得到分离,轻质油相从溢流管上部分流出,重质水相从溢流管下部分流出。试验3#内侧的油相分布大于试验7#,所以试验3#有着更高的分离效率,即与正交试验分析结论有着一致性。
通过对螺旋管正交优化试验结果的直观分析,可以得出变距螺旋管结构参数匹配的最佳方案为A1B3C2,参照表1表头设计的参数配比,按照A1B3C2参数完成最优方案螺旋管分离器流体域结构模型建立,并在操作参数相同的边界条件下开展螺旋管油水分离性能的数值模拟分析,得出分离效率为57.94%,分离效率略高于3#试验。
如图6所示,分别选取优化前尺寸参数与优化后尺寸参数的模型分离效率进行对比,得出其分离效率随入口处理量的变化对比图。 由图可知,随着处理量的不断增大,其分离效率都逐渐增大,但是优化后尺寸参数的模型在任意相同流量情况下,优化后的变距螺旋管油水分离效率较优化前有明显提升。

图5 试验3#和试验7#外部油相分布云图Fig.5 External oil phase distribution cloud diagrams for 3# test and 7# test

图6 处理量对分离性能的影响Fig.6 Effect of processing capacity on separation performance
进一步选取不同分流比,进行优化前尺寸参数与优化后尺寸参数的螺旋管油水分离效率对比分析,得出不同分流比条件下优化前后螺旋管分离性能对比曲线如图7所示。由图7可以分析出,随着分流比的不断增大,其分离效率都表现为先增大后减小,但是优化后尺寸参数的模型在任意相同分流比情况下,分离效率明显高于优化前的模型,且在其最大效率为66%时,达到最佳分流比20%。
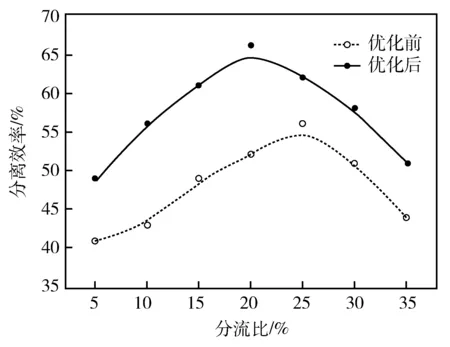
图7 分流比对分离性能的影响Fig.7 Influence of split ratio on separation performance
6 结 论
1) 变距螺旋分离器的螺旋管锥角、螺旋管圈数、溢流管直径都会对其分离性能产生影响,且对分离性能的影响显著性由大到小分别为螺旋锥角、螺旋管圈数及溢流管直径。
2) 通过正交试验优化,得出设计的变距螺旋管最佳螺旋锥角为5°、最佳螺旋管圈数为7圈、最佳溢流管直径为70 mm,优化后分离器结构的油水分离效率为57.34%,较初始结构提高了7.24%。
3) 其他条件相同的情况下,优化后的变距螺旋管结构分离效率随入口处理量的增大呈升高趋势,由2.0 m3/h升高到5.0 m3/h时,分离效率由40%提高到69.5%,优化后结构最佳分流比为20%。

