集束动态海底电缆截面机械性能分析

石 涵， 李 阳， 郭 宏， 杨继明， 李 博， 张 磊， 于治雨

(1. 中海石油(中国)有限公司深圳分公司，深圳 518000；2. 中海油研究总院有限责任公司，北京 100028；3. 江苏亨通高压海缆有限公司，常熟 215000)

0 引 言

随着海洋能源的发展，海底电缆的需求越来越大，并且逐渐出现不同类型的海底电缆[1-4]。其中，集束海底电缆(简称海缆)是一种针对水下多设备同时供电需求而设计的光电复合缆，属于多层级螺旋缠绕、非黏结的复合结构。动态缆在满足功能要求的同时，还要考虑其在安装、运行过程中各种载荷作用下的安全可靠性。缆的截面性能分析是其他分析的基础，对于后续在位设计及疲劳分析具有重要意义。

在工程应用中，主要采用理论公式法[5-8]和3D有限元法[9-14]进行海洋管缆的截面性能计算：理论公式法计算便捷，但在计算过程中常常需要大量简化假设，因此有较大误差，适用于初期的快速迭代设计；3D有限元法基于精细单元模型，计算结果精确度高，能可视化展示结果，但是由于模型中存在大量接触，导致收敛问题突出，时间成本较高。

基于UFLEX有限元分析软件，本文建立了能够考虑螺旋构件的轴向效应的二维平面模型，并以某南海项目集束动态海缆为例，进行了截面力学性能分析。与理论结果进行对比发现，模拟值与理论值吻合得较好，验证了有限元分析模型与建模技术的可行性和正确性，为海缆快速设计提供了一种可行的解决方法。

1 集束动态海缆截面结构

南海某油田水深约为400 m，采用浮式液化天然气生产储卸装置(floating liquefied natural gas system， FPSO)和水下系统结合的开发方式。FPSO通过一根集束动态海缆为三套水下设备供电并通信，动态海底电缆结构如图1所示，主要由2层铠装钢丝、3组电单元和1根光单元螺旋缠绕构成，每组电单元又由3组铜导体子芯螺旋缠绕构成。

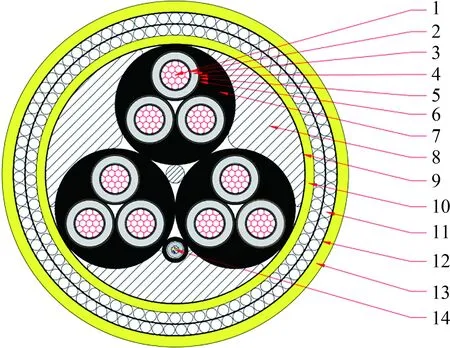
1—铜导体；2—导体屏蔽；3—绝缘；4—绝缘屏蔽；5—铜带屏蔽；6—绑扎带；7—相护套；8—异形填充；9—绑扎带；10—内护套；11—铠装钢丝；12—绑扎带；13—外护套；14—光缆图1 动态海底电缆结构Fig.1 Dynamic submarine cable structure

2 数值模型

UFLEX是海缆专用的非线性有限元分析软件，可以采用2.5D方法，即二维截面有限元计算与轴向效应理论计算结合的方式，进行海缆的截面应力分析。本文采用UFLEX 2D对海缆在准静态加载下的情况进行应力分析。

2.1 模型简化

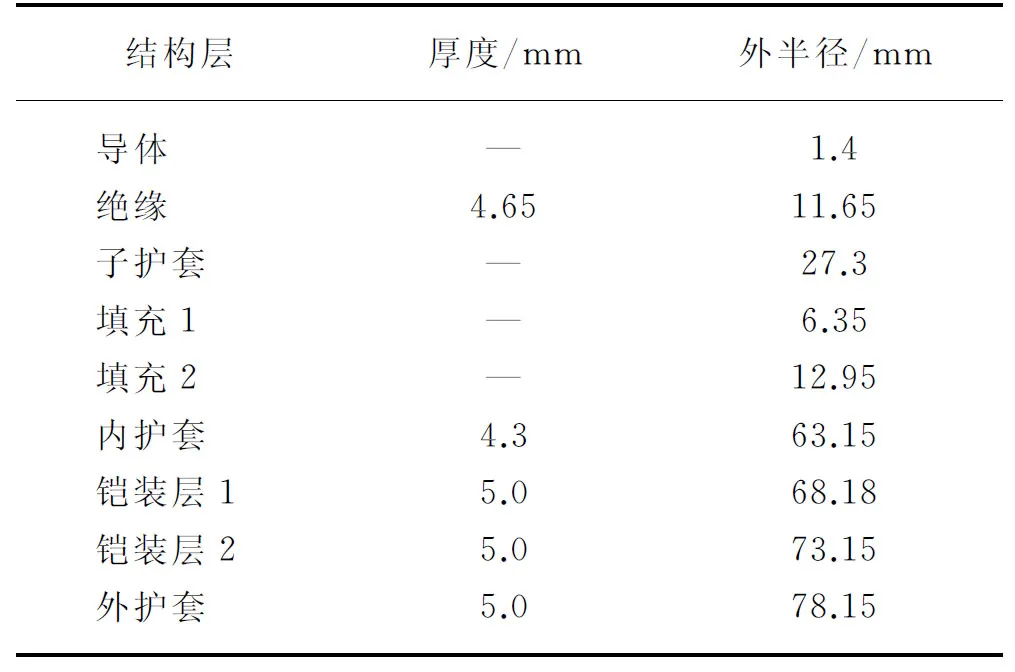
考虑到铜带屏蔽、绑扎带、光缆等结构对海缆的刚度影响较小，因此在建模时可忽略；同时考虑到导体屏蔽、绝缘和绝缘屏蔽材料大致相同，因此在建模时可作为一层结构；异形填充主要是在生产中保持海缆椭圆度及传递载荷的作用，为了计算简便，可用3个圆形填充替代。经过上述结构上的简化，海缆数值模型结构参数如表1所示。

表1 海缆数值模型结构参数

Tab.1 Strutural parameters of sea cable numerical model

同时考虑到缠绕等轴向效应，还需各单元的缠绕根数和节距，如表2所示。

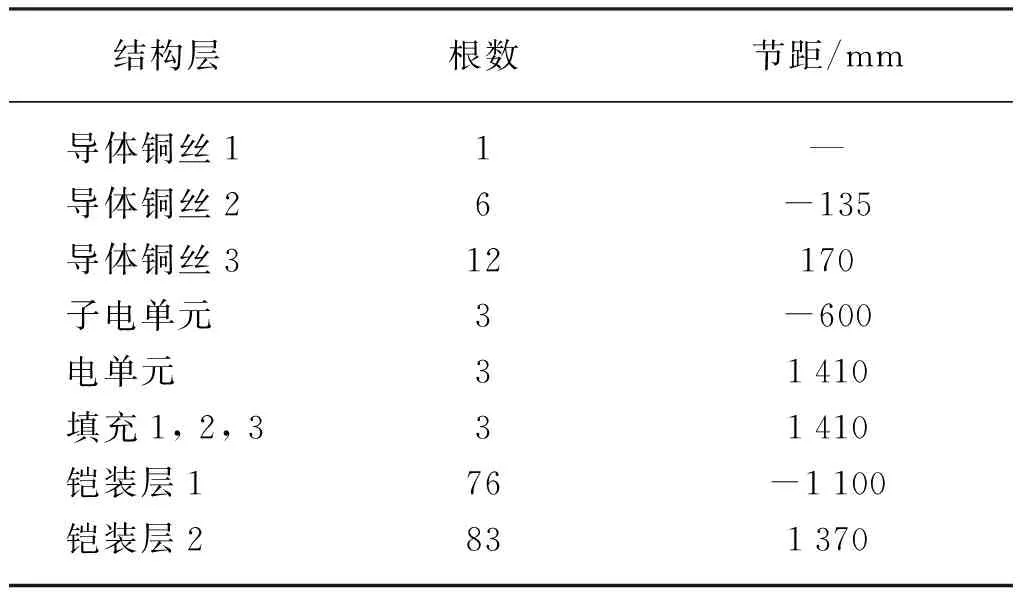
表2 单元缠绕参数

子电单元是由导体、绝缘组成的单元，而电单元是由3个子电单元、相护套组成的单元。

可根据上述参数绘制CAD图形，并从CAD中读取组件的位置、几何参数，在UFLEX 2D建立二维截面模型(见图2)。

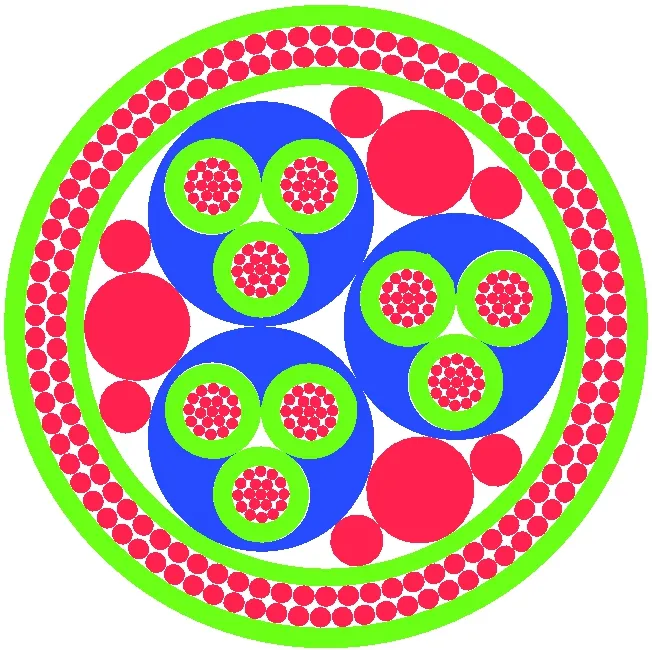
图2 几何模型Fig.2 Geometric model

数值模型中的各材料的物理性能参数如表3所示。其中导体主要材料为铜，铠装层材料为钢，而绝缘层、子护套、填充、内护套和外护套材料均为PE。

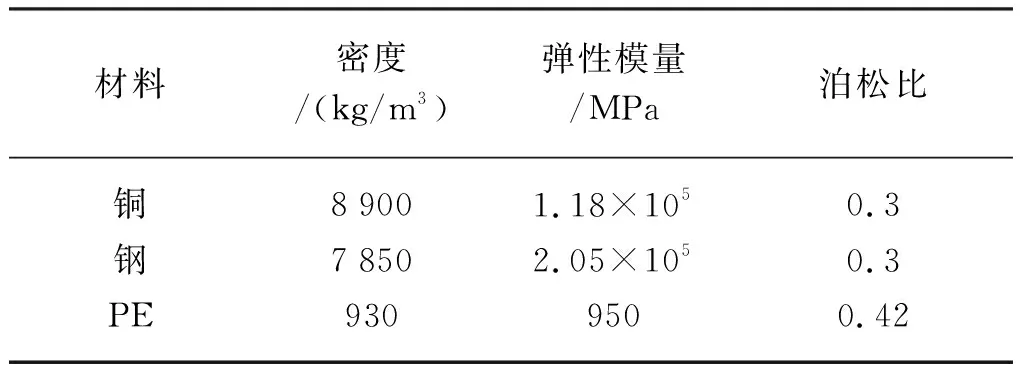
表3 材料的物理性能参数

2.2 仿真设置

当施加张力时，缆内部各层单元向着内部中心紧缩，各单元间互相接触，产生相互作用。各单元间需要设置接触。当划分网格时，从属表面的网格应该比主控表面的网格更密，如果网格密度相同，从属表面所占的部分应该选择较软的材料。对于铠装钢丝等实心结构则采用BEAM单元，而绝缘层、护套等空心结构则采用SHELL单元，网格划分如图3所示。

图3 网格划分Fig.3 Meshing

缆体结构的刚度主要是给出载荷与缆体变形的关系。因此在计算轴向刚度时，只施加轴向拉力；在计算弯曲刚度时，只施加弯矩载荷；在计算扭转刚度时，只施加扭矩，以约束其他方向的自由度。因为考察的是整个海缆截面刚度而不仅仅是加强构件的刚度，所以拉力、弯矩、扭矩等载荷是作为集中载荷施加在模型截面上的。

3 结果分析与验证

基于上述设置方法，对海缆施加相应的载荷，迭代计算，以关键单元应力达到屈服应力为准，本案例中关键单元为铠装钢丝，其应力云图如图4所示。

由力学分析可知，缆的轴向刚度为轴向拉力与缆的轴向应变的比值。因此提取拉力与对应的轴向应变历史数据，拟合后得到拉力-应变曲线，如图5所示。缆的轴向刚度即拉力-应变曲线的斜率，数值为514 MN。

缆的弯曲刚度为所受弯矩与缆的曲率的比值。因此提取弯矩与对应的曲率的历史数据，拟合后得到弯矩-曲率曲线，如图6所示。图中曲线明显分为两段，开始一段较陡峭，后一段较平缓，这是因为刚

开始曲率较小，各单元间尤其是钢丝处在静摩擦阶段，当曲率超过临界时，钢丝产生滑动，变为滑动摩擦。在工程应用中，取较小值是保守的。因此缆的弯曲刚度取平缓段弯矩-曲率曲线的斜率，数值为14.54 kN·m2。

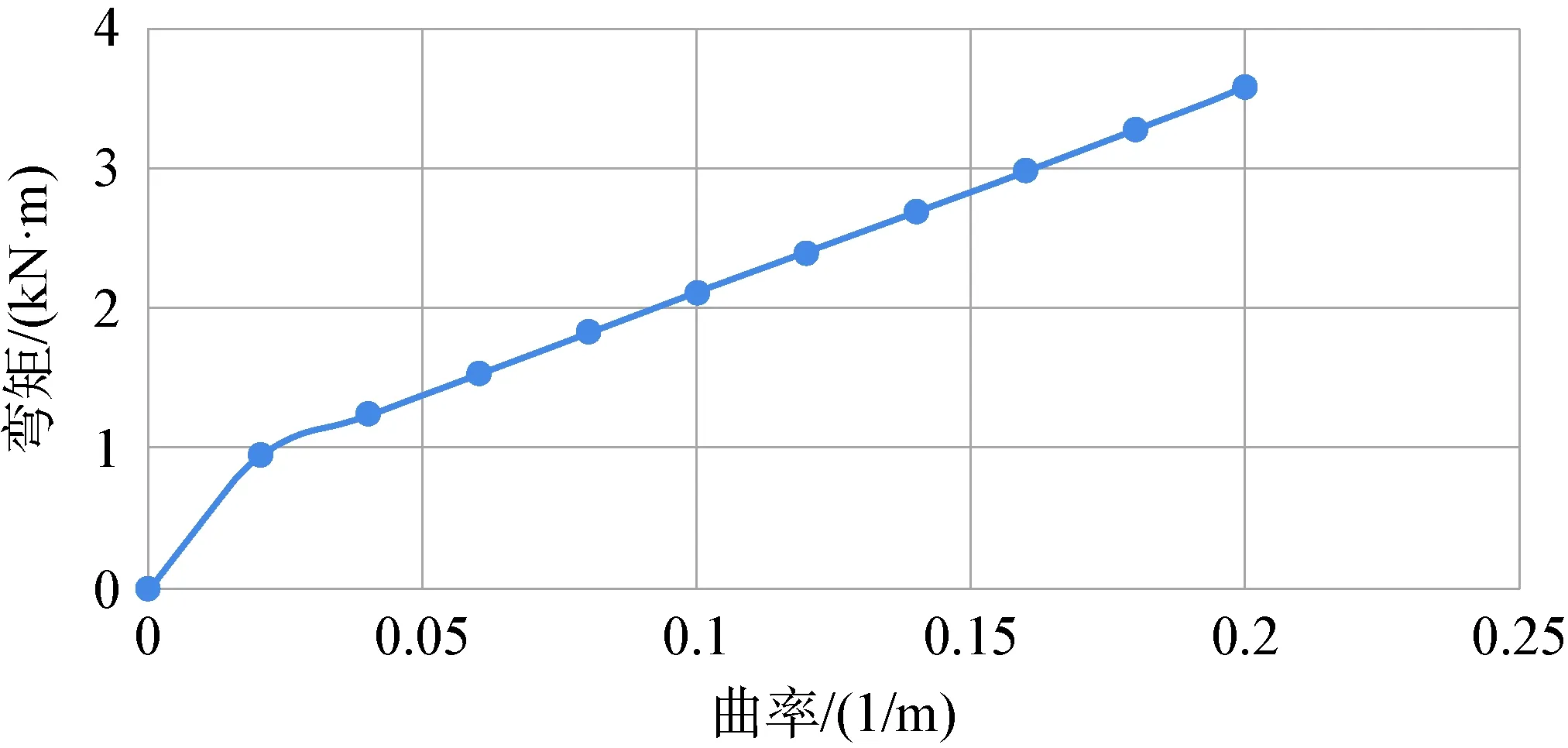
图6 弯矩-曲率曲线Fig.6 Bending moment-curvature curve

缆结构是典型的多单元螺旋缠绕结构，不同结构层的缠绕方向不同，导致缆体扭转性能在逆时针和顺时针两个方向上也必然有所差异。在设计动态缆截面时，需要考虑顺时针扭转刚度和逆时针扭转刚度基本一致，保证缆体的扭转平衡，否则将导致海缆在安装过程中出现扭曲，甚至破坏。

缆的扭转刚度为所受扭矩与缆的单位扭转角的比值。因此提取扭矩与对应的单位扭转角的历史数据，拟合后得到扭矩-转角曲线，如图7所示。

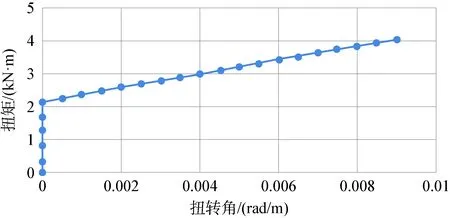
图7 扭矩-转角曲线(顺时针)Fig.7 Torsion moment-torsion angle cure (clockwise)

由图7可知，缆的顺时针扭转刚度为211.0 kN·m2。

由图8可知，缆的逆时针扭转刚度为212.3 kN·m2。

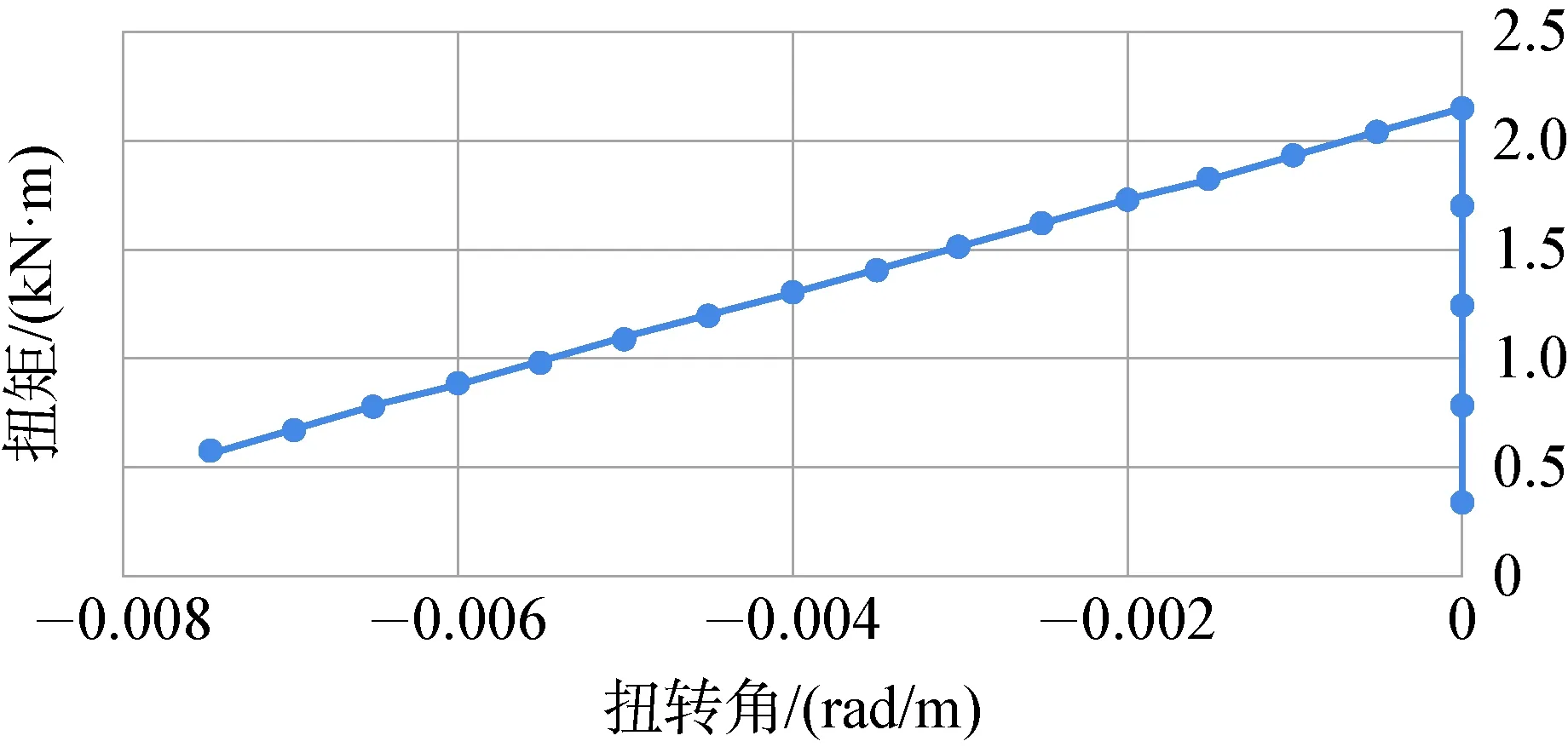
图8 扭矩-转角曲线(逆时针)Fig.8 Torsion moment-torsion angle cure (anti-clockwise)

在实际应用中，人们并不会特意区分顺时针和逆时针，因此缆的扭转刚度要在两者中取较小值，以保证缆在使用时的安全性。

为验证有限元模型和建模技术的正确性，将数值分析结果与理论分析结果进行比较。在理论计算中，根据纳普(Knapp)模型得到的整体拉伸刚度解析公式为

(1)

式中：Ai、Ei、Ri、αi分别为第i个螺旋构件的截面面积、弹性模量、节圆半径、沿管缆轴向的螺旋角；n为螺旋构件的个数；θ为不可压缩系数(当假设中心圆柱体为刚性时，值取为0；当假设中心圆柱体为不可压缩时，值取为1)；Rc和EcAc分别为中心圆柱的半径和拉伸刚度。

弯曲刚度则采用维茨(Witz)模型，该模型忽略摩擦影响，且假定同一功能层各构件的弯曲变形一致，全滑动状态下的整体弯曲刚度计算公式：

(2)

式中：EI0为直构件的弯曲刚度；EiIi为第i根螺旋构件的弯曲刚度；αi为第i个螺旋构件沿管缆轴向的螺旋角。

根据纳普提出的经典拉扭理论模型，可得到扭转刚度计算公式：

(3)

式中：GcJc为中心圆柱的扭转刚度。

将集束动态海缆的相关参数代入以上各式，可得到对应的刚度理论值。理论分析与数值模拟的结果以及两者之间的误差如表4所示。轴向刚度和弯曲刚度模拟值与理论值相差不大；扭转刚度模拟值与理论值相差略大，推测原因是模拟中考虑了铜导体的扭转，而理论中则是将铠装内部都假设为PE材料的中心圆柱，而且忽略了摩擦和接触的影响。从工程设计的角度来看，三者都符合得很好，可在一定程度上验证有限元分析模型与建模技术的正确性。

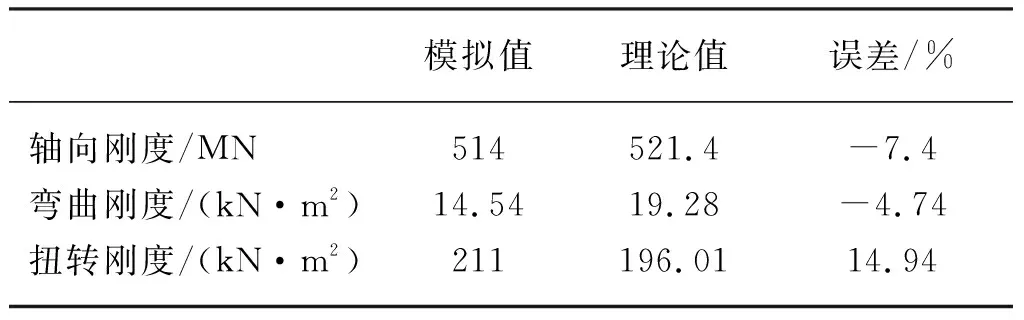
表4 刚度模拟值与理论值的对比

理论解析结果和有限元模拟结果存在一定偏差，这是由于在建立理论解析数学模型时，进行了适当的简化和假设。在后续研究中，需要通过试验验证进行模型与建模方法上的完善和改进。

4 结 语

本文基于UFLEX有限元分析软件，建立了能够考虑螺旋构件的轴向效应的二维平面模型。以某南海项目集束动态海缆为例，进行算例分析，并将轴向刚度、弯曲刚度和扭转刚度等结果与理论结果进行对比，吻合程度较高，验证了有限元分析模型与建模技术的可行性和正确性，在满足计算精度的要求同时能显著提高计算效率，可在设计初期就得到更全面、更详细的截面受力情况，为满足海缆快速设计需求和设计前期的结构优化提供了一种可行的解决方法。