盾构隧道注浆纠偏数值模拟研究

高翔，龚晓南，朱旻，黄晟，刘世明，严佳佳

盾构隧道注浆纠偏数值模拟研究

高翔1，龚晓南1，朱旻1，黄晟1，刘世明2，严佳佳3

(1. 浙江大学 滨海与城市岩土工程研究中心，浙江 杭州 310058；2. 华东勘测设计研究院有限公司，浙江 杭州 311122；3. 浙江省智慧轨道交通工程技术研究中心，浙江 杭州 311122)

为研究注浆纠偏在隧道工程中的应用规律，对深圳地铁1号线鲤鱼门—前海湾区间的注浆纠偏工程进行介绍。据现场注浆纠偏结果显示，外部注浆可有效纠正隧道横向偏位，竖向注浆纠偏效果不如水平注浆纠偏效果。提出一种应用于实际工程模拟注浆的数值方法。依托实际注浆纠偏工程，通过有限元软件ABAQUS，运用提出的注浆模拟方法建立考虑浆液注入的二维流固耦合模型。从注浆管打设角度、注浆压力和注浆范围3个角度，对通过打设斜管注浆对隧道进行竖向纠偏的规律进行研究。研究结果表明：注浆管角度为60°时，对隧道竖向直径收敛减小效果较好，角度越大，对竖向位移纠偏效果越好。注浆压力不宜超过600 kPa。向下延伸注浆范围可以提升注浆纠偏的效果。

盾构隧道；注浆；纠偏；数值模拟

随着中国工业化、城镇化的高速进行，有限的土地资源越来越紧张。为了提高土地资源的利用率，对土地进行集约化开发，地下空间开发需求得到不断增长。地铁是地下空间开发的核心和主要内容[1]。盾构隧道作为城市地铁的主要结构形式，其结构安全关乎地铁的安全运营。盾构隧道由管片通过螺栓连接成型，故随地铁运营时间的增长、隧道周边环境的变化等因素的影响，盾构隧道可能会产生不均匀偏位、变形，进而出现管片开裂、错台、渗漏水、道床脱空等病害。针对上述各类病害，目前已发展出了裂缝芳纶布补强、注浆堵漏、隧道外注浆加固、环氧封缝、黏钢加固等多种治理方法。其中注浆已成为盾构隧道水平偏位、不均匀沉降的常用治理方法。并已在上海、南京、天津等地的工程[2−10]中进行了实践。依文献[2]~[10]，此方法已在多处粉土、黏土地层盾构隧道的过大收敛及水平偏位等病害治理中得到应用。注浆范围基本位于隧道外侧与隧道等高且平齐的土层中，距隧道外侧距离在3~5 m左右。由文献[2]~[10]可知，各工程所采用的浆液相似，说明目前在注浆施工中，注浆参数的选取多借鉴类似工程。但各盾构隧道的埋深、土层性状、病害程度不尽相同，注浆效果有限，且并无明显的规律性。提升注浆在工程实践中的应用效果，依赖于相关研究的进一步深入。目前已有不少国内外学者从土体变形状况、浆液扩散规律、浆液扩散范围及注浆后土体性状等多个角度对注浆进行了研究[11−17]，但少有学者针对隧道外注浆对隧道及周围土体的影响进行规律性探究。本文依据深圳地铁1号线注浆纠偏工程，运用ABAQUS有限元软件进行数值分析。提出了基于Cohensive单元的注浆模拟方法，通过有限元与实测的对比验证数值模型的合理性，并研究了不同注浆管角度、注浆压力及注浆范围下隧道的变形发展规律。研究结论可以对工程实践产生一定的指导作用。

1 工程概况

深圳地铁1号线鲤鱼门~前海湾区段(以下简称鲤前区间)运营期间，其南侧地块正在进行基坑施工。基坑距离此区间左线隧道最短水平距离约37.5 m。因受基坑开挖降水影响，鲤前区间发生偏位，该区间最大累积沉降达78.6 mm，往基坑侧最大水平位移达28.4 mm。由于此偏位会严重威胁地铁的正常运营，故考虑隧道所在场地无任何地上建构筑物后，依专家建议采用在隧道上方卸土和在隧道周围土体中注浆相结合的方式进行纠偏。

1.1 场地条件

所在场地为海积平原，表层杂填土层下依次为第四系全新统海积淤泥、海冲积黏性土、粉土、砂土、残积砂质黏性土、砾质黏性土，下伏燕山期花岗岩和全风化~中等风化花岗岩。隧道主要穿越黏土、砂质黏土和全、强风化花岗岩，淤泥地层基本位于隧道拱顶上1 m。地下水位为地表以下2.9 m。隧道区间穿越的土层地质分布详见表1。

1.2 注浆纠偏流程介绍

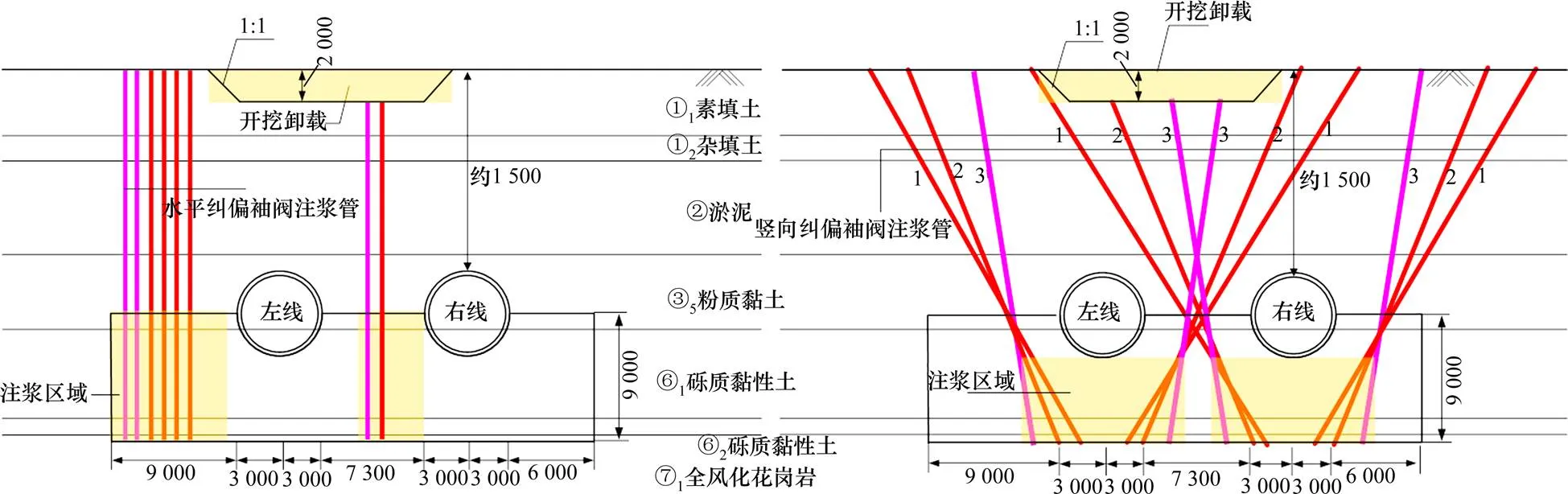
具体注浆纠偏流程如图1所示。

表1 鲤前区间土层力学参数

单位：mm

注浆纠偏流程：1) 卸载：对双线隧道上方土体进行放坡开挖，开挖槽顶宽约17 m，开挖深度2 m；2) 水平注浆纠偏：在盾构隧道左侧布置注浆管进行压密注浆。如图1从左至右依次为第1~8排注浆孔，其中第1~2排及第7排注浆孔(从左向右)用于形成止浆墙，其余各排起主要纠偏作用。图1中隧道轴线下9 m范围为水平注浆孔注浆区域；3)竖向注浆纠偏：在盾构隧道两侧对称打设斜向注浆管进行压密注浆。注浆管下部距盾构隧道由近及远依次为第1，2和3排注浆孔对。同竖向注浆管，第1排注浆孔(图1中数字1标识)用于形成止浆墙，其余2排起主要纠偏作用。第1~3排注浆孔与水平面所呈夹角依次为81°，67°和57°。

2 注浆模拟方法介绍

针对注浆过程的模拟，国内外不少学者都已提出各自模拟方法。李晓龙等[18]研究过浆液在岩体裂隙中的运移机制。唐智伟等[19]提出过在土体中施加“虚拟”膨胀压力增加单元体积的方法来模拟注浆。杨秀竹[20]运用数值方法对弹性饱和多孔介质压密注浆时土体内部应力及位移进行研究。王朝亮等[21]提出注浆球孔压扩散模型。 Cividini[22]推导出含溶质的浆液渗流控制方程。Bolisetti等[23]提出了考虑胶凝过程的非均质多孔介质注浆模拟模型。CHEN等[24]提出模拟土中劈裂注浆发展过程的数值方法。

虽然上述学者所提方法仿真效果较好，但主要针对注浆过程本身，未将注浆工程修复对象考虑在内，且模拟方法较为复杂，相关计算参数难以在工程中获得。

其中通过施加虚拟膨胀压力来扩张土体以模拟注浆的方法存在一定问题。虚拟膨胀压力的选用会影响模拟结果。其值无据可定，纯凭经验，且与实际工程中的注浆压力值难以对应，故对工程实践的指导意义有限。此外，其方法采用式(1)来确定土体体积应变增量。由式(1)可知，此方法较适用于小渗透系数黏土中的快速注浆，未考虑注浆过程中浆液的渗流及浆液可能沿裂隙的迁移，因此实际的土体体积应变量应小于实际注浆量，且土体体积应变量在实际工程中难以测量。

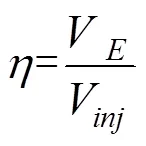
其中：为注浆效率；V为由于注浆引起的土体膨胀体积；V为注浆体积。

另外，李亚勇等[25]通过研究发现，在数值计算中考虑地下水情况的隧道安全系数较不考虑地下水时将降低20%左右。而上述涉及注浆对隧道影响的研究大都不考虑地下水的影响。

故本文为方便运用工程数据对注浆进行模拟，并提高计算精确度，基于ABAQUS有限元分析软件提出了流固耦合的模拟注浆方法。

本方法可用于饱和土中注浆的模拟。具体方法：1) 划分注浆区域：由于本方法主要应用于实际工程，而实际工程模型通常较为复杂，模型整体尺寸可能较注浆管尺寸大百倍以上，为简化模型用一线段代替注浆区域(如图2)。2) 插入cohesive单元：选取代表注浆区域的线段插入0厚度Cohesive单元。在实际注浆过程中，浆液将先填充注浆管，再逐渐渗出并作用于周边土体。本文通过在Cohesive单元上预设初始裂缝来实现这一过程的模拟。Cohesive单元的fluid leakoff参数依不同注浆过程的模拟而进行不同设置。渗透注浆过程中，浆液颗粒尺寸小于土颗粒间的孔隙尺寸，浆液可在土体中自由流动，浆液颗粒与浆体同步流动。故模拟渗透注浆时，Cohesive单元参数中的fluid leakoff应设为该浆液在土体中的渗透系数。压密注浆过程，浆液会占据原有土体空间，并不断挤压注浆孔周围土体，形成浆泡，仅有少量浆体渗入周围土体。浆土间会形成明显界面。故当模拟压密注浆时，认为浆液不会渗入周围土中，Cohesive单元参数中fluid leakoff应设置为10−10cm/s。Cohesive单元的Gap flow参数依所采用浆液的黏度进行设置。3) 浆液的注入：选取Cohesive单元上的节点作为浆液的注入点，具体的注入方式可依实际工程方案设定压力控制式或流量控制式。

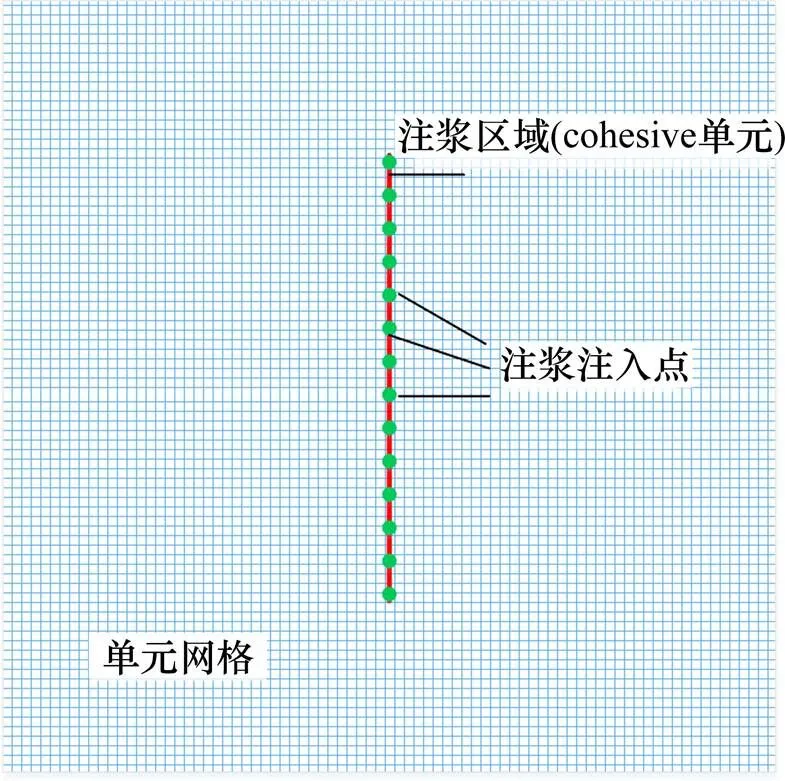
图2 注浆模拟说明

本文方法的优点：数值模型中注浆点所设注浆压力接近实际工程中的注浆压力或浆液流量，可对浆液的动态注入过程进行研究，且可对渗透注浆和压密注浆2种注浆方式进行模拟。

3 注浆方法的验证

以上述纠偏工程为例，对本文提出的注浆模拟方法进行验证。

3.1 数值计算模型

由于隧道区间倾斜度为17‰，土层分布也较为均匀，故本文采用二维模型以简化计算。模型尺寸为 55 m×35 m，隧道外径 6.0 m，内径 5.4 m，隧道顶部埋深 15 m左右，两隧道轴线距离约 13 m。地下水水位线在地表以下2.9 m处。隧道轴线下9 m处为注浆区，距离隧道外径最小距离为3 m。其余相对位置关系及尺寸详见图3~4。

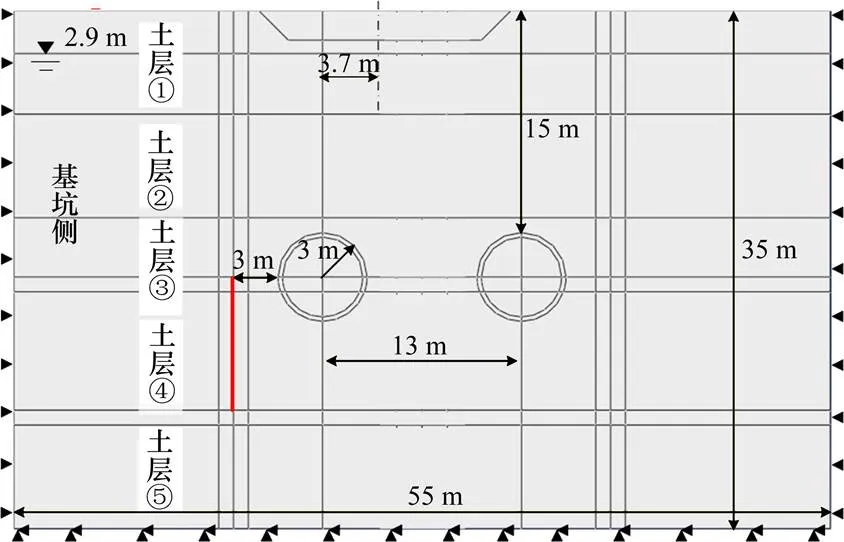
图3 水平注浆纠偏模拟图

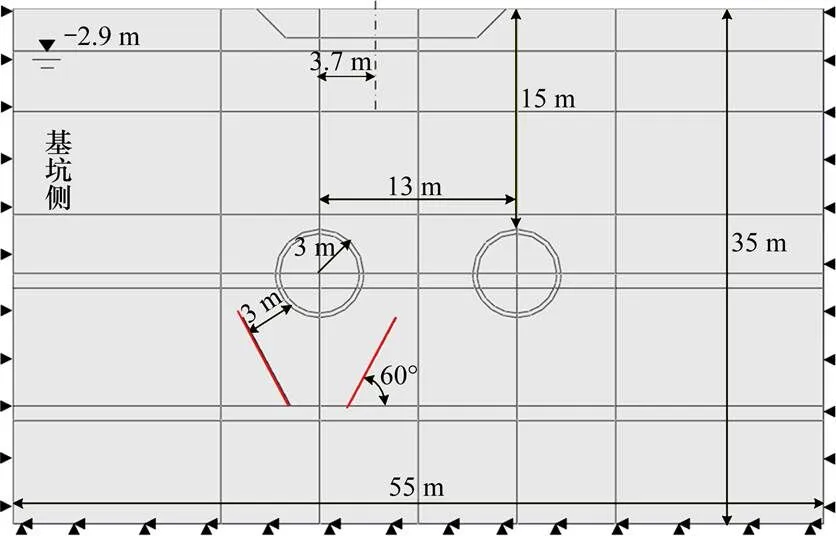
图4 竖向注浆纠偏模拟图

数值计算模型边界条件如下：地表为位移自由边界；底部边界位移限制为0；模型侧边界约束法向位移。模型中土体均采用二维4节点平面应变孔压单元(CPE4P)；管片采用二维4节点平面应变单元(CPE4)，注浆区采用cohesive单元，在注浆区靠基坑侧设置水平约束。

3.2 计算参数

参考汤渊[26]在数值模拟中所采用的盾构衬砌弹性模量折减方法。深圳地铁盾构隧道衬砌采用C50混凝土，弹性模量E=3.45×104MPa，考虑接缝和螺栓的影响，取10%～15%的折减系数，且根据现场检查结果，隧道管片存在一定的损伤，故最后取混凝土弹性模量为2.6×104MPa，容重为 25 kN/m3，泊松比 0.15。

为简化模型以便于计算，将实际土层中性质相近的土层合并为单一土层。数值模型中的土层按表2参数设置。

表2 数值模型土层参数设置

注浆区Cohesive单元弹性模量，依上节所提出的注浆模拟方法，按注浆区所在土层弹性模量设置。此次模拟为压密注浆，依上节所提出的注浆模拟方法，Cohesive单元fluid leakoff按渗透系数10−10cm/s设置。浆液黏度参考文献[27]取100。

3.3 数值模拟过程

注浆纠偏工程模拟过程如下：首先参考陈大川等[28]的模拟方法，采用生死单元方法完成盾构隧道衬砌安装，即在地应力平衡阶段先移除盾构隧道模型单元，待地应力平衡完成后再激活所移除的模型单元。其次在双线隧道上分别施加位移荷载实现隧道初始偏位。在水平注浆模拟中，左线隧道向基坑侧水平偏移20 mm，沉降50 mm，右线隧道向基坑侧偏移10 mm，沉降20 mm。在实际工程中，竖向纠偏紧接水平纠偏，故在模拟竖向纠偏注浆中，考虑水平注浆对隧道产生的纠偏，左线隧道设置向基坑侧水平偏移5 mm，沉降40 cm，右线偏位同水平注浆模拟设置。待土中孔压不再发生变化后，再进行地表卸荷开挖及侧向注浆加固。注浆压力为300 kPa，注浆时间依工程实际，当到达设计终压并继续注浆10 min即可停止，模拟中耗时720 s。最后以注浆引起的相关位移和变形为指标，研究注浆对隧道变形的影响规律。依据现场监测结果，本文仅以注浆引起的隧道水平直径位移、竖向位移变化及隧道收敛为指标开展验证分析。水平注浆模拟计算工况与竖向注浆模拟计算工况一致，详见表3。

3.4 结果对比与分析

为验证数值模拟的合理性，将数值结果与现场实测隧道横向变形和竖向变形进行对比分析。由于在水平纠偏中，用于右线隧道水平纠偏的第7和8排注浆管未能起到纠偏作用，且在竖向纠偏中，左右线注浆互不干扰，故本文只对左线隧道注浆纠偏过程进行模拟。注浆过程详见表4和表5。

表3 注浆模拟计算工况

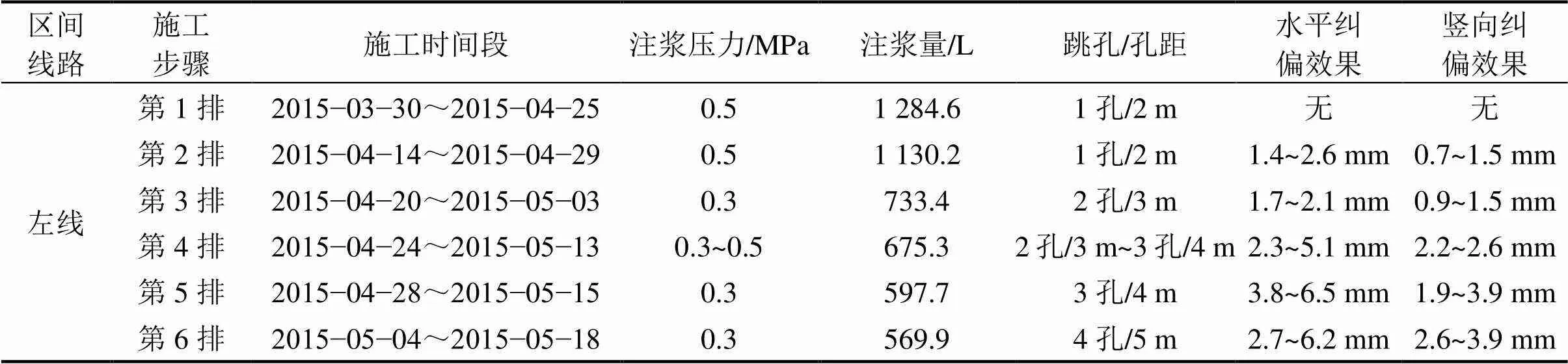
表4 水平注浆纠偏施工过程

表5 竖向注浆纠偏施工过程

数值模拟结果与实测结果的对比详见表6和表7。

表6 水平注浆结果对比

表7 竖向注浆结果对比

由上2表可见，实测与数值计算结果规律基本一致，故说明本文数值模拟方法合理。但除水平注浆模拟结果及竖向注浆模拟中水平纠偏效果外，其余纠偏效果皆与工程实际存在一定出入。

经分析，导致模拟结果与实际存在出入的原因：1) 在实际工程中先行注浆的几排注浆管会形成止浆墙，并为后排注浆管提供类似反力墙的作用。而本文方法无法考虑注浆后土体的强化，因此采用在注浆区靠基坑侧一面施加水平位移约束的方法来模拟先注区所形成的反力墙。此法高估了先排注浆管所形成的止浆墙和反力墙效果，故水平注浆模拟结果略高于工程实际结果。2) 由表4~5所示注浆过程可见，竖向纠偏紧接水平纠偏，由于实际工程未对水平注浆后土体的基本力学性质进行测试，故本文在模拟过程中未考虑水平注浆纠偏后周边土体的强化。3) 本文所建模型为二维模型，而实际工程为三维空间，浆液在注入过程中还会对衬砌环平面外土体产生作用，故模拟结果较实际结果偏大。由上述分析可见，实测与数值计算结果的差异主要由模型简化过程产生，并不涉及数值模拟方法本身。

4 相关参数影响分析

由上文总结可知外部注浆工法在实际工程已有一定应用。但大多采用打设竖直袖阀管注浆，对隧道水平偏位进行纠偏。少有用外部注浆法对隧道沉降进行回调的案例。本工程为保证在纠偏过程中不影响隧道的正常运营，而采用外部注浆对隧道沉降进行回调。

为探究通过打设斜管注浆以纠偏隧道的工法能否在类似隧道修复工程中作为一种减小施工影响的可行方法，本文将围绕注浆压力、注浆管打设角度及注浆范围3个参数，运用数值模拟对斜管注浆纠偏隧道进行参数分析。

为排除其他因素在注浆过程中的影响，本文对上述数值模型做了一定的调整。模型尺寸调整为42 m×35 m，只考虑单线隧道，不考虑地表土开挖卸载及隧道初始偏位。其余土层参数，隧道埋深、尺寸等皆同原模型。

4.1 注浆管角度

注浆管角度为注浆管与水平面所呈夹角。如图5本文选取了50°，60°，70°和80° 4种工况进行分析。各工况下，注浆管距盾构隧道最近距离为3 m，注浆范围为自隧道底向下6 m范围。根据《城市轨道交通结构安全保护技术规范》，盾构隧道周边3 m范围内不得进行任何施工。参考本工程双线隧道间距(约13 m)，50°及以下的注浆管在打设过程中会进入盾构隧道周边严禁施工范围，但为探究不同注浆管打设角度对注浆纠偏效果的影响，本文选取了50°的注浆管角度作为下限。

注浆管角度对隧道竖向直径收敛变化及隧道竖向位移的影响如图6所示，图6中隧道竖向位移分别采用隧道竖向直径两端点的竖向位移表示。由于水平直径收敛变化规律与竖向直径变化规律一致，且数值接近，故图6中隧道直径变化仅以竖向直径变化为研究对象。由图6可见，各角度竖向注浆对于隧道竖向位移的调整作用要好于对竖向直径收敛和水平直径收敛的调节作用。竖向直径收敛效果随注浆管角度变化平缓，其中以注浆管角度为60°时效果最好，竖向直径收敛变化达15.4 mm。随着注浆管角度的增加，隧道竖直上移量亦不断增加。在注浆管角度小于70°时，上移量变化较为平缓，当注浆管角度大于70°时，上移量增加较为显著。

综上分析，注浆管角度的变化对于隧道竖向直径收敛和竖向位移的调节并不一致。因此，实际工程宜根据隧道病害类型及严重程度选择合适的角度。若主要以减小竖向直径收敛，宜取60°的注浆管角度进行注浆纠偏。若主要以沉降回调，宜取较大的注浆管角度进行注浆。

4.2 注浆压力

盾构隧道发生沉降时，若不均匀沉降较小，过大的隧道直径收敛将会成为危及盾构隧道安全运营的主因，故参考上文关于注浆管角度的分析结果，本小节将基于60°的注浆管角度对注浆压力进行研究。

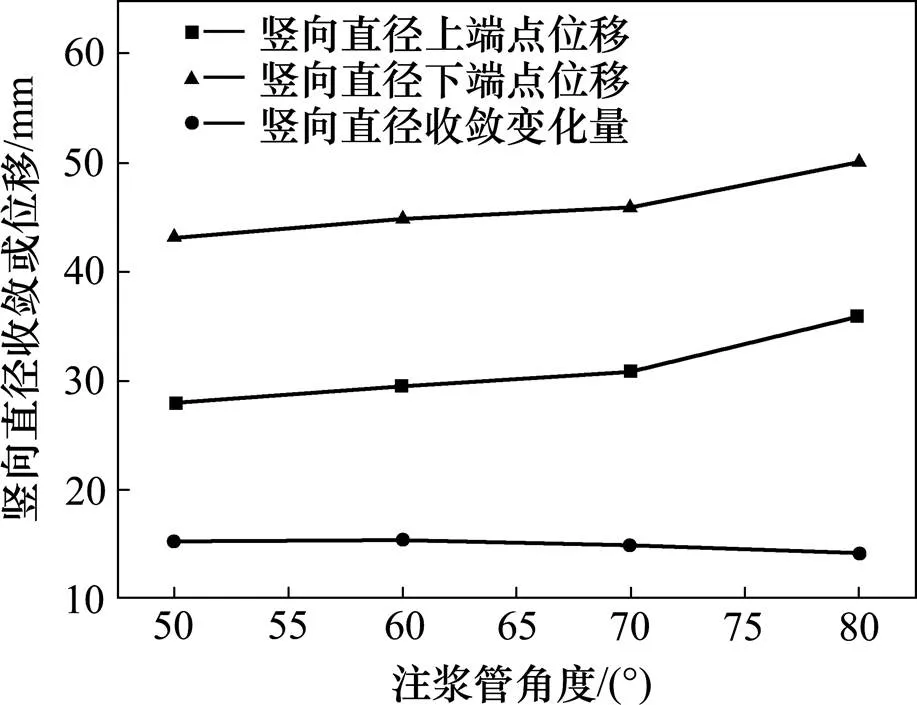
图6 注浆管角度对隧道竖向直径收敛及隧道竖向位移的影响

由于工程实例注浆压力控制在300~800 kPa，故本文设置了150，300，450，600，750和900 kPa共6个工况。各工况下注浆管角度均为60°，除注浆压力有别外，其余参数皆与上小节注浆管角度60°工况一致，即与注浆管角度分析中的工况2一致。

注浆压力对隧道竖向直径收敛变化及隧道竖向位移的影响如图7所示。由图7可见，竖向直径两端点的上移量随注浆压力的增长呈二次增长，但考虑到M-C本构模型属于理想弹塑性模型，无法考虑土体应力历史。且在实际注浆中，当土体因注浆压力过大而发生破坏后，浆液可能会沿着破坏面进行填充，故土体实际变形应小于计算结果，尤其在注浆压力较大的情况下。因此当注浆压力越大，该数值模型计算结果的失真度越高。竖向直径收敛变化则较为平缓，竖向直径收敛减小量并不会随注浆压力的增加而增大，由图7及表8可见，竖向直径收敛减小量达到最大时，注浆压力在300~450 kPa。

综上分析，注浆压力的变化对于隧道竖向直径收敛和竖向位移的调节并不一致。较大的注浆压力可以带来显著的隧道沉降回调，但是过大的注浆压力虽为隧道沉降回调带来了显著的效果，也可能会给隧道周边带来不利影响，故根据分析结果，并考虑本构模型选取所带来的误差后，本文认为在距隧道3 m时，注浆压力应控制在600 kPa内。

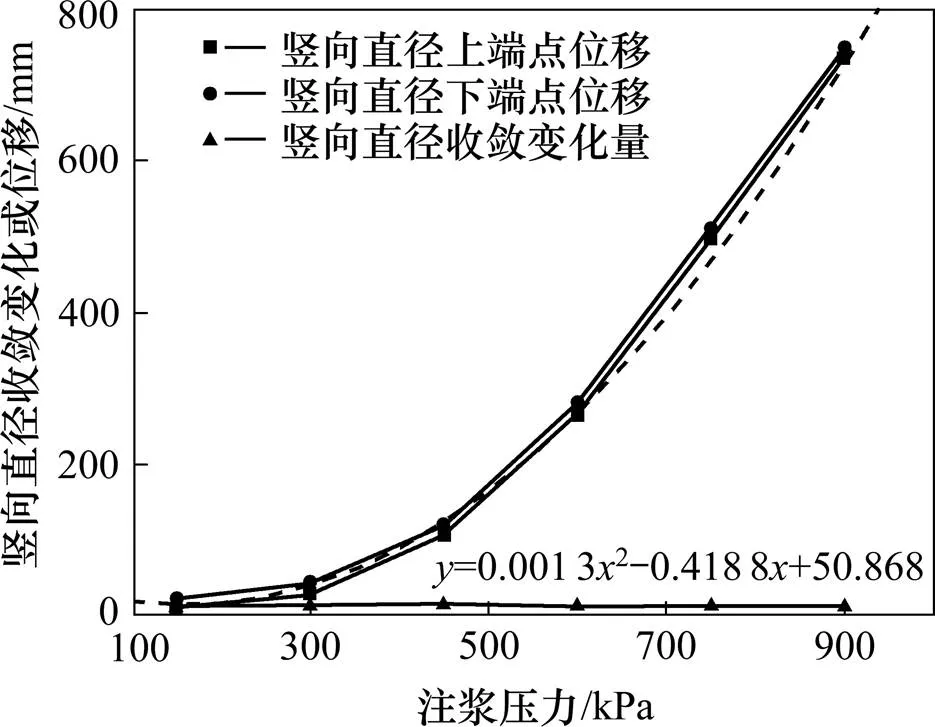
图7 注浆压力对隧道竖向直径收敛及隧道竖向位移的影响

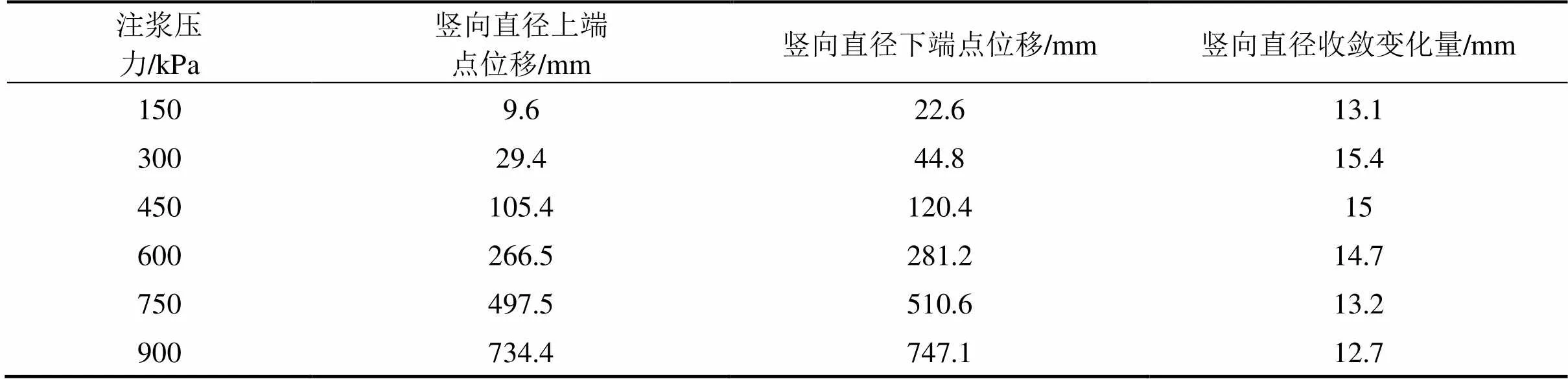
表8 注浆压力对隧道竖向直径收敛及隧道竖向位移的影响

4.3 注浆范围

本工程在注浆纠偏中为了达到更好的纠偏效果，尝试将斜孔孔深增加3 m，同时增对应注浆范围，并将注浆范围向上增加3 m形成封闭，防止冒浆现象。本文为探究斜孔注浆范围对于注浆效果的影响，设置了如图8的5种工况，图8中各工况皆为示意。各工况皆基于注浆管角度60°的设置，距隧道最近皆为3 m，仅调整注浆范围。其中注浆管角度60°，注浆范围为隧道底下方6 m为注浆范围研究中的工况2。工况1在工况2的基础上将注浆范围向下延伸3 m。工况3在工况2的基础上将注浆范围向上延伸至隧道轴线高度。工况4在工况2的基础上将注浆范围向上延伸至隧道顶高度。工况5注浆范围为隧道下方9 m至隧道顶。

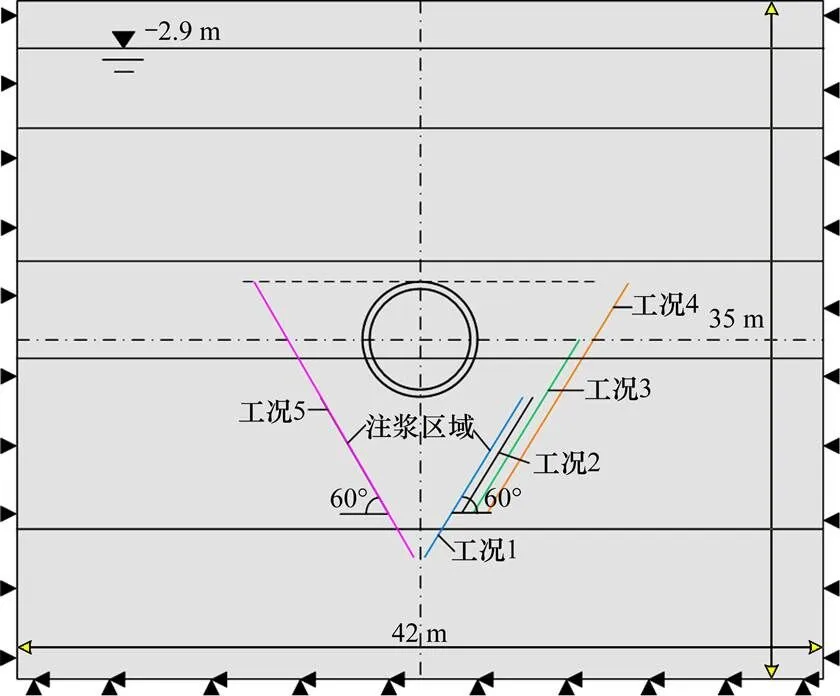
图8 注浆范围分析

注浆范围对隧道竖向直径收敛变化及隧道竖向位移的影响如图9 所示。对比工况1和工况2可以发现，向下延伸注浆范围对于提升隧道沉降回调量，效果较为显著，但对减小竖向直径收敛效果一般。对比工况2~4可见，向上延伸注浆范围对于隧道沉降回调效果较好，但隧道竖向直径收敛减小量显著下降。工况4下，隧道竖向直径收敛反而增大。对比工况4和5也可发现向下沿延伸注浆范围可以改善隧道竖向位移回调效果和竖向直径收敛减小效果。

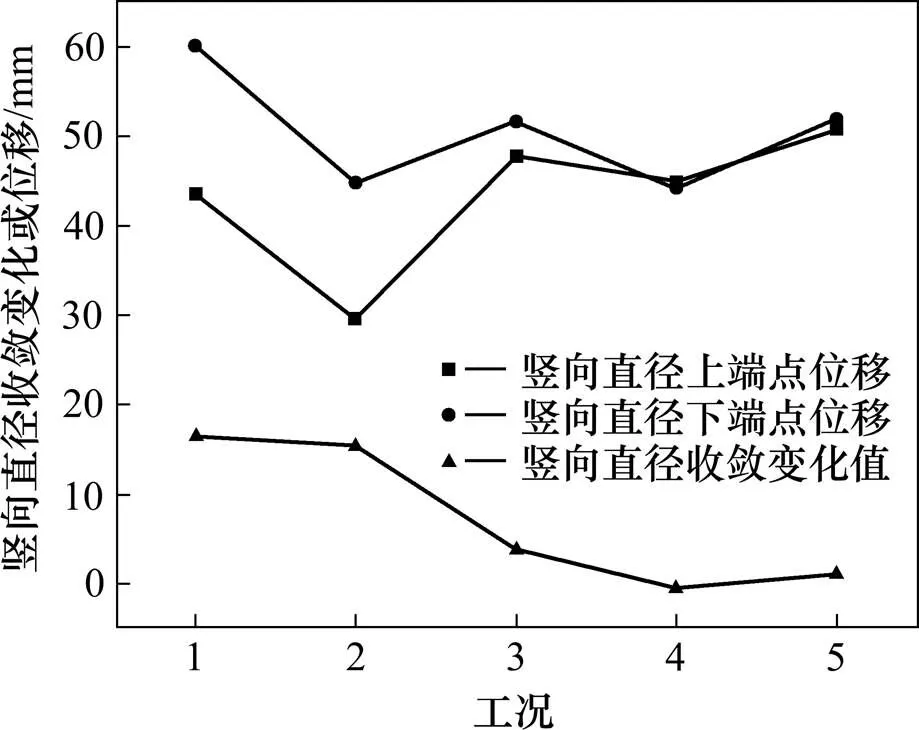
图9 注浆范围对隧道竖向直径收敛及隧道竖向位移的影响

综上分析，实际工程中若期望较好的竖向位移回调效果和竖向直径收敛减小，宜向下延伸注浆范围。若仅希望改善隧道竖向位移，可考虑向上延伸注浆范围，但向上延伸范围不宜超过隧道顶。

5 结论

1) 根据工程实测数据，在隧道外进行注浆确实能起到较好纠偏效果。在本工程中，水平注浆对隧道水平及竖向纠偏的效果皆较斜管注浆时较好。经工程实例验证，本文提出的注浆数值模拟方法合理。具可模拟渗透注浆和压密注浆、可对应实际工程注浆参数等优点。

2) 依本文对斜管注浆参数的研究，注浆管角度对于隧道竖向位移变化的影响与对竖向直径收敛变化的影响并不一致。当注浆管角度为60°时，对竖向直径收敛减小效果最好，较大或较小的注浆管角度皆会降低对竖向直径收敛减小的效果。而随注浆管角度的增大，竖向位移的纠偏效果逐渐变好。

3) 注浆压力对隧道竖向位移变化的影响与对竖向直径收敛变化的影响也不一致。隧道因注浆而引起的上移量会随注浆压力的增大而增大，且上移增量也会不断增大。但依本文的分析，当注浆压力控制在300~450 kPa时，隧道竖向直径收敛减小效果较好。因注浆过程不应对隧道及周边产生较大影响，且此模型自身存在局限，故斜管注浆压力宜控制在600 kPa内。

4) 基于对斜管注浆范围的研究，发现注浆范围向下延伸将会增强注浆对隧道竖向位移及竖向直径收敛减小的效果。但向上延伸注浆则会减弱纠偏效果，甚至加剧隧道收敛。

[1] 孙钧. 国内外城市地下空间资源开发利用的发展和问题[J]. 隧道建设, 2019, 39(5): 699−709. SUN Jun. Development and some issues on exploitation and utilization of urban underground space in China and abroad[J]. Tunnel Construction, 2019, 39(5): 699−709.

[2] 夏汉庸, 刘畅, 陈鼐基. 盾构隧道注浆抬升浆液配制技术[J]. 城市轨道交通研究, 2016, 19(9): 120−124. XIA Hanyong, LIU Chang, CHEN Naiji. On the grout configuration for shield tunnel grouting Up lift[J]. Urban Rail Transit Research, 2016, 19(9): 120−124.

[3] 刘训华. 盾构隧道纵向不均匀沉降的压密注浆控制技术[J]. 隧道与轨道交通, 2014(1): 16−20. LIU Xunhua. Compaction grouting technology for shield tunnel longitudinal uneven settlement control[J]. Underground Engineering and Tunnels, 2014, 23(1): 16− 20.

[4] 朱瑶宏, 夏汉庸, 胡志飞. 软土地层盾构隧道结构整体抬升实践[J]. 岩土力学, 2016, 37(增2): 543−551. ZHU Yaohong, XIA Hanyong, HU Zhifei. An uplifting practice of shield tunnel in soft ground[J]. Rock and Soil Mechanics, 2016, 37(Suppl 2): 543−551.

[5] 刘建航, 王如路, 汪小兵. 上海轨交运营隧道检修制度和沉降治理技术难题对策[J]. 地下工程与隧道, 2013(1): 1−6. LIU Jianhang, WANG Rulu, WANG Xiaobing. Shanghai rail transit tunnel maintenance system and countermeasures to technical difficulties of settlement treatment[J]. Uuderground Engineering and Tunnels, 2013(1): 1−6.

[6] 高永. 微扰动双液注浆纠偏技术在南京地铁盾构隧道病害治理中的应用[J]. 城市轨道交通研究, 2015, 18(6): 109−112. GAO Yong. Application of micro disturbance correction technique for double liquid grouting in shield tunnel disease treatment of Nanjing metro[J]. Urban Rail Transit Research, 2015, 18(6): 109−112.

[7] 况龙川. 深基坑施工对地铁隧道的影响[J]. 岩土工程学报, 2000, 22(3): 284−288. KUANG Longchuan. Influence of construction of deep foundation pit on tunnels of metro[J]. Chinese Journal of Geotechnical Engineering, 2000, 22(3): 284−288.

[8] 张冬梅, 刘梓圣, 阎静雅. 软土盾构隧道横向大变形侧向注浆控制机制研究[J]. 岩土工程学报, 2014, 36(12): 2203−2212. ZHANG Dongmei, LIU Zisheng, YAN Jingya. Effective control of large transverse deformation of shield tunnels using grouting in soft deposits[J]. Chinese Journal of Geotechnical Engineering, 2014, 36(12): 2203−2212.

[9] 陈凯骅, 方涛, 蔡大伟, 等. 工程建设对邻近地铁隧道产生变形影响后的微扰动注浆修复工艺与效果分析[J]. 工程建设与设计, 2017(23): 119−123. CHEN Kaihua, FANG Tao, CAI Dawei, et al. Analysis of micro-disturbance grouting repair technology and effect on the deformation influence of adjacent metro tunnel of engineering construction[J]. Municipal Traffic Water Resources Engineering Design, 2017(23): 119−123.

[10] 陈潇, 俞雪薇, 黄亚德. 某隧道微扰动注浆施工变形分析[J]. 施工技术, 2017(增1): 756−759. CHEN Xiao, YU Xuewei, HUANG Yade. Deformation analysis of certain tunnel construction with micro disturbance grouting[J]. Construction Technology, 2017(Suppl 1): 756−759.

[11] Schweiger H F, Kummerer C, Otterbein R, et al. Numerical modelling of settlement compensation by means of fracture grouting[J]. Soils and Foundations 2004, 44(1): 71−86.

[12] El-Kelesh A M, Mossaad M E, Basha I M. Model of compaction grouting[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2001, 127(11): 955− 964.

[13] Soga K, Au S K A, Jafari M R, et al. Laboratory investigation of multiple grout injections into clay[J]. Geotechnique, 2004, 54(2): 81−90.

[14] 王小龙, 王起才, 张戎令, 等. 水泥−水玻璃双液注浆力学特性的试验研究[J]. 铁道科学与工程学报, 2016(10): 1926−1932. WANG Xiaolong, WANG Qicai, ZHANG Rongling, et al. Experimental study on mechanical characteristics of cement−silicate double solution grouting[J]. Journal of Railway Science and Engineering, 2016(10): 1926−1932.

[15] 欧阳进武, 张贵金, 刘杰. 劈裂灌浆扩散机理研究[J]. 岩土工程学报, 2018, 40(7): 1328−1335. OUYANG Jinwu, ZHANG Guijin, LIU Jie. Diffusion mechanism of split grouting[J]. Chinese Journal of Geotechnical Engineering, 2018, 40(7): 1328−1335.

[16] 张连震, 刘人太, 张庆松, 等. 软弱地层劈裂–压密注浆加固效果定量计算方法研究[J]. 岩石力学与工程学报, 2018, 37(5): 1169−1184. ZHANG Lianzhen, LIU Rentai, ZHANG Qingsong, et al. Calculation of reinforcement effect of fracturing- compaction grouting in soft strata[J]. Chinese Journal of Rock Mechanics and Engineering, 2018, 37(5): 1169− 1184.

[17] 龚柳, 李剑波, 陈雄武. 运营地铁盾构隧道纠偏整治技术及自动化监测研究[J]. 公路与汽运, 2018(4): 150− 158. GONG Liu, LI Jianbo, CHEN Xiongwu. Research on correction and remediation technology and automatic monitoring of subway shield tunnel[J]. Highways & Automotive Application, 2018(4): 150−158.

[18] 李晓龙, 罗晓倩, 钟燕辉, 等. 基于FVM和VOF的平面裂隙注浆数值模型[J]. 水力发电学报, 2018, 37(5): 145−153. LI Xiaolong, LUO Xiaoqian, ZHONG Yanhui, et al. Numerical model of planar fracture grouting based on FVM and VOF[J]. Journal of Hydroelectric Engineering, 2018, 37(5): 145−153.

[19] 唐智伟, 赵成刚. 注浆抬升地层的机制、解析解及数值模拟分析[J]. 岩土力学, 2008, 29(6): 1512−1516. TANG Zhiwei, ZHAO Chenggang. Mechanisms of ground heave by grouting and analytical solutions and numerical modeling[J]. Rock and Soil Mechanics, 2008, 29(6): 1512−1516.

[20] 杨秀竹. 静动力作用下浆液扩散理论预实验研究[D]. 长沙: 中南大学, 2005. YANG Xiuzhu. Study on grouting diffusion theory and experiments under static or dynamic loading[D]. Changsha: Central South University, 2005.

[21] 王朝亮, 苟长飞. 盾构隧道壁后注浆球孔压滤扩散模型[J]. 铁道科学与工程学报, 2017, 14(12): 2670−2677. WANG Chaoliang, GOU Changfei. Spherical cavity pressure filtration expansion model of the back-filled grouts in shield tunnel[J]. Journal of Railway Science and Engineering, 2017, 14(12): 2670−2677.

[22] Cividini A. An experimental and numerical study of the low-pressure grouting of granular soils by diluted chemical solutions[J]. International Journal of Geomechanics, 2001, 1(4): 415−439.

[23] Bolisetti T, Reitsma S. Grouting and ground treatment-numerical simulation of chemical grouting in heterogeneous porous media[C]// American Society of Civil Engineers Third International Conference on Grouting and Ground Treatment-New Orleans, Louisiana, United States, 2003: 1454−1465.

[24] CHEN T L, ZHANG L Y, ZHANG D L. An FEM/VOF hybrid formulation for fracture grouting modelling[J]. Computers and Geotechnics, 2014(58): 14−27.

[25] 李亚勇, 张桂凤, 靳晓光. 基于流固耦合的强度折减法研究地下水渗流对隧道稳定性的影响[J]. 铁道科学与工程学报, 2017, 14(3): 585−592. LI Yayong, ZHANG Guifeng, JIN Xiaoguang. The effect of groundwater seepage on stability of tunnel by using strength reduction method considering fluid solid coupling[J]. Journal of Railway Science and Engineering, 2017, 14(3): 585−592.

[26] 汤渊.地铁车站曲线顶管暗挖新方法数值模拟研究[J].地下空间与工程学报, 2014, 10(3): 650−655.TANG Yuan. Investigation on a new curved pipe jacking tunneling method for subway station using numerical simulation[J]. Chinese Journal of Underground Space and Engineering, 2014, 10(3): 650−655.

[27] 杨建康, 陆海军, 李继祥, 等. 水泥−水玻璃双液注浆材料工程性能及孔隙结构[J]. 大连理工大学学报, 2016, 56(3): 252−256. YANG Jiankang, LU Haijun, LI Jixiang, et al. Engineering properties and pore structure of cement- sodium silicate double solution grouting material[J]. Journal of Dalian University of Technology, 2016, 56(3): 252−256.

[28] 陈大川, 胡建平, 董胜华. 盾构施工对临近浅基础框架结构影响的研究[J]. 铁道科学与工程学报, 2017, 14(3): 552−559. CHEN Dachuan, HU Jianping, DONG Shenghua. Research on the influence of shield construction on the nearby shallow foundation frame structure[J]. Journal of Railway Science and Engineering, 2017, 14(3): 552−559.

Numerical simulation of grouting remediation in shield tunnel

GAO Xiang1, GONG Xiaonan1, ZHU Ming1, HUANG Sheng1, LIU Shiming2, YAN Jiajia3

(1. Research Center of Coastal and Urban Geotechnical Engineering, Zhejiang University, Hangzhou 310058, China;2. East China Investigation Design Institute Under CHECC, Hangzhou 311122, China;3. Zhejiang Intelligent Rail Transit Engineering Technology Research Center, Hangzhou 311122, China)

To study the application law of grouting remediation in Tunnel Engineering, firstly, the remediation of the Liyumen-Qianhaiwan section of Shenzhen Metro Line 1 was introduced. According to the remediation project, the results show that external grouting can effectively rectify the lateral displacement of the tunnel. The effect of vertical grouting is not as good as the effect of horizontal grouting. A numerical method applied to the simulation of the grouting in practice is proposed. Based on the remediation project, a two-dimensional fluid-solid coupling model considering grouting process was established in the ABAQUS by using the numerical method. The effect of vertical grouting on the tunnel is studied considering three factors, which are the angle of the grouting pipe, grouting pressure and the grouting range. The research shows that when the angle of the grouting pipe is 60°, the remediation of the vertical diameter convergence of the tunnel can achieve the best effect. The larger the angle, the better effect on the remediation. Grouting pressure should not exceed 600 kPa. Extending the grouting range downwards can improve the effect of the remediation.

shield tunnel; grouting; remediation; numerical simulation

O319.56

A

1672 − 7029(2020)06 −1480 − 11

10.19713/j.cnki.43−1423/u.T20190742

2019−08−24

国家自然科学基金资助项目(51778575，51338009)；浙江省重点研发资助项目(2018C03G3241274)

龚晓南(1944−)，男，浙江金华人，教授，博士，从事地基处理和复合地基工程研究；E−mail：xngong@hzcnc.com

(编辑 蒋学东)