基于改进TOPSIS法研究隧道施工方案优化

吴波，路明，雷领，黄惟，黄宗辉

基于改进TOPSIS法研究隧道施工方案优化

吴波1, 2，路明1, 2，雷领3，黄惟1, 2，黄宗辉1, 2

(1. 广西大学 土木建筑工程学院，广西 南宁 530004；2. 广西大学 工程防灾与结构安全教育部重点试验室，广西 南宁 530004；3. 中交路桥建设有限公司，北京 101116)

由于城市地铁周围环境复杂，隧道稳定性难以得到保证，故合理地选择隧道施工方案是顺利施工的前提。考虑到客观环境和人工操作等因素，选择开挖顺序，初支封闭时间，加固范围和参数作为影响隧道稳定性的主要因素，并根据影响因素构建L16(4×4)正交表进行正交试验，对试验方案进行数值模拟。以隧道收敛变形和围岩应力为评价指标，建立改进TOPSIS评估模型，并将最优方案用于北京地铁17号线天通苑站项目。研究结果表明：工况5的相对贴近度最低，其值为0.182 7，故工况5为最优方案；最优方案比实际工程地表沉降小5.9%，说明改进TOPSIS法是可以广泛应用于浅埋暗挖大断面隧道工法优化，对于复杂隧道工程也有借鉴意义。

隧道工程；最优方案；改进TOPSIS法；浅埋暗挖隧道；正交试验

近年来，我国城市地铁快速发展，建设数量和建设里程逐年增加。城市地铁浅埋暗挖大断面隧道，因其跨度大，施工工序复杂，对围岩造成多次扰动，地表沉降难以控制，施工难度大[1]，风险高。合理选择施工方案是隧道顺利竣工的前提，针对影响浅埋暗挖大断面隧道的稳定性因素，调整隧道施工参数，以保证隧道施工过程中的稳定性。大多研究者采用数值模拟、模型试验、理论研究和现场监测数据等方法研究影响隧道稳定性的因素。来弘鹏等[2]采用现场试验研究加固区范围及其参数对隧道稳定性的影响规律；FANG等[3]通过数值模拟和施工监测研究隧道施工顺序对隧道稳定性；XUE等[4]采用改进粗糙集理论分析影响隧道稳定性的因素，得出隧道初支封闭时间是影响隧道稳定性最重要的因素；吴波[5]基于控制理论和动态规划原理，研究地表沉降变化规律；王新民等[6]采用AHP—TOPSIS法对采矿方案进行优化，虽然方法简单，计算量小，但评价指标权重主观性较强，精确度不高；邬晓光等[7]采用海明距离—TOPSIS直觉模糊数学法对隧道扩挖方案进行优化，但定性分析和定量分析未充分结合，具有一定的局限性。传统TOPSIS[8−9]法定性分析和定量分析未充分结合，评价指标权重分配主观性强，对于特殊性指标无法灵活处理，评价结果令人差强人意。因此采用灰色关联度[10]和组合赋权法[11]对传统TOPSIS法进行改进。本文根据影响隧道稳定性的因素，构建L16(4×4)正交表进行正交试验[12]，把地表沉降、围岩应力、右侧导洞拱顶沉降、拱腰水平位移作为评判指标，用熵值法[13]和模糊层次分析法[14]进行组合赋权，增强其准确性和客观性，最后采用改进TOPSIS法对隧道施工稳定性进行评判，贴近度越低说明该方案越好，隧道稳定性也越好。

1 改进TOPSIS法

1.1 TOPSIS法计算D+和D−

将地表沉降、围岩应力、拱腰水平位移以及右侧拱顶沉降作为评价指标，根据评价指标建立矩阵：

对其进行规范化处理，并对处理后的数据进行赋权，其中T通过组合赋权法求得：

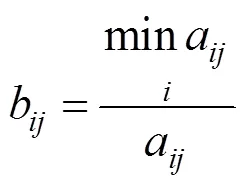
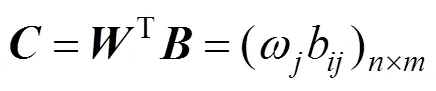
根据式(4)～(5)，确定理想方案和负理想方案：

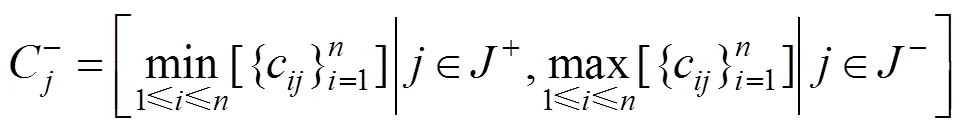
公式中J表示正向指标，J表示负向指标。

根据(6)～(7)，确定理想解和负理想解的欧氏 距离：

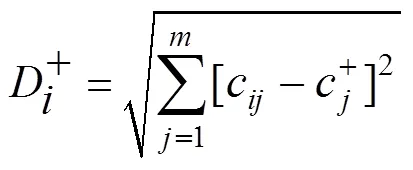
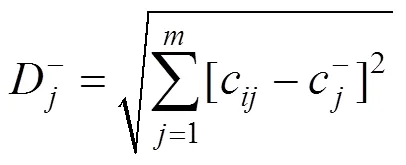
1.2 灰色关联度法计算R+，R−和λ

根据(2)～(3)式处理后的矩阵变为矩阵，用(3)式对矩阵和正、负理想解C和C进行处理。

并对灰色关联度和TOPSIS进行加权处理，代表作者偏好，本文取0.5。

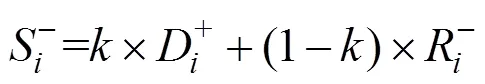
最后计算相对贴近度，并进行排序：

1.3 组合赋权方法

1.3.1 熵值法

对指标矩阵进行归一化处理：

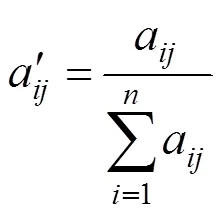
各指标的信息熵：

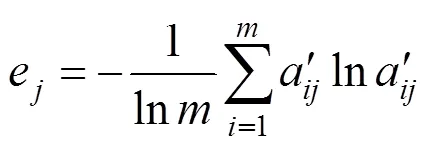
熵值法权重：

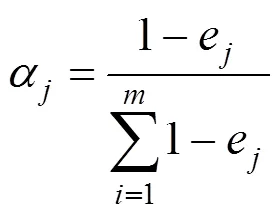
1.3.2 主观赋值法

本论文采用模糊层次分析法计算主观权重。

1.3.3 组合权重

本文将按照文献[13]中的组合权重进行计算，具体公式如下：

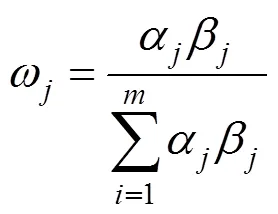
2 工程实例

北京地铁17号线天通苑站歇甲村出入段线南肢项目，矿山法暗挖隧道里程为RDK0+138~ RDK0+421暗挖长度283 m(单洞双线)，其中YKO+ 365.343~YKO+405.367段为连续渐变隧道，断面面积在95~123 m2范围，B型断面和C型断面以及渐变段隧道均属于大断面隧道，渐变隧道轮廓如图1所示。

图1 隧道连续渐变段

本文采用动态分区方法(DPM)，将隧道分为2部分。Ⅰ为固定分区部分，其隧道跨度固定在10 m，临时支撑把固定分区分为4个临时小导洞，分别为Ⅰ-1，Ⅰ-2，Ⅰ-3，Ⅰ-4，采用CRD法施工；Ⅱ为动态分区部分，它可以随着隧道轮廓的增加而增加，从而实现隧道渐变。动态分区分为2个小导洞，即Ⅱ-5和Ⅱ-6，采用台阶法施工。为了满足项目的需要，最大宽度为4.5 m，最小值为2.3 m。在本文中，研究最大断面隧道，因此为4.5 m，隧道总跨度为14.5 m。但是仍需要讨论Ⅰ和Ⅱ部分之间的错开距离。DPM动态分区如图2所示。

2.1 数值模型计算

对北京地铁17号线渐变大隧道原始方案进行数值分析，选取歇甲村出入段线南肢暗挖隧道断面面积最大的C段，跨度为14.5 m，高为10.91 m，埋深为7.5 m。围岩级别为Ⅵ级，模型方向120 m，方向60 m，方向47 m，见图3。

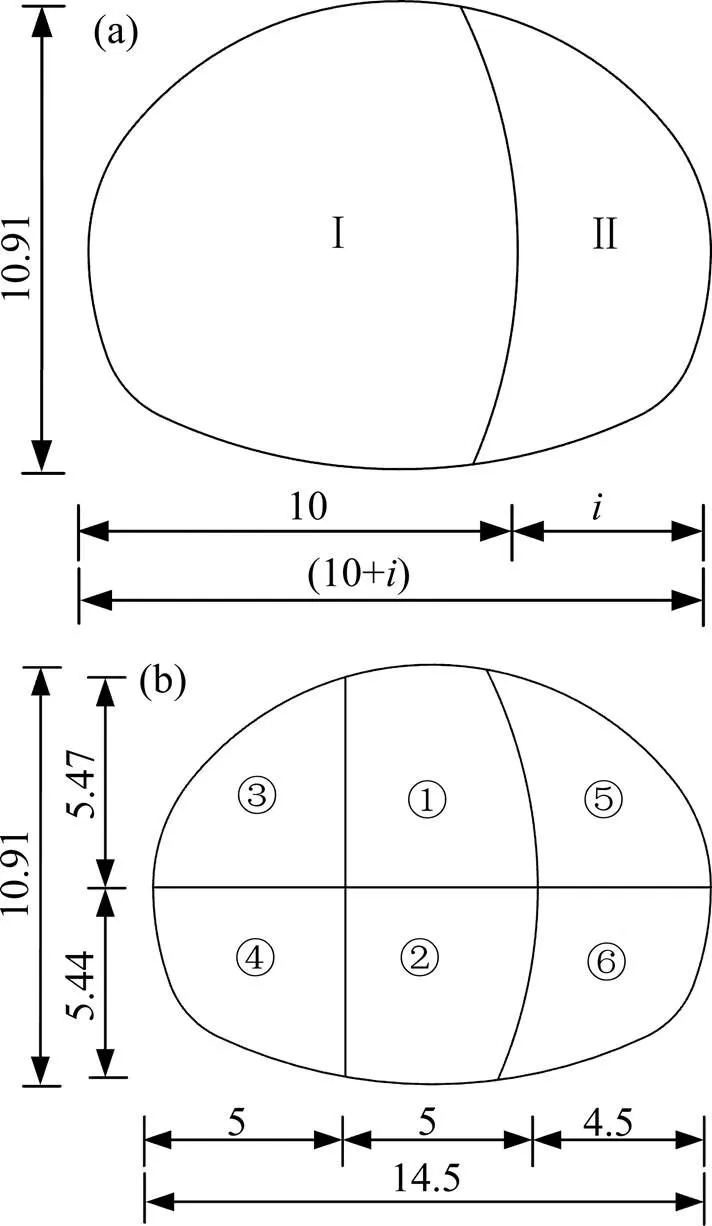
单位：m

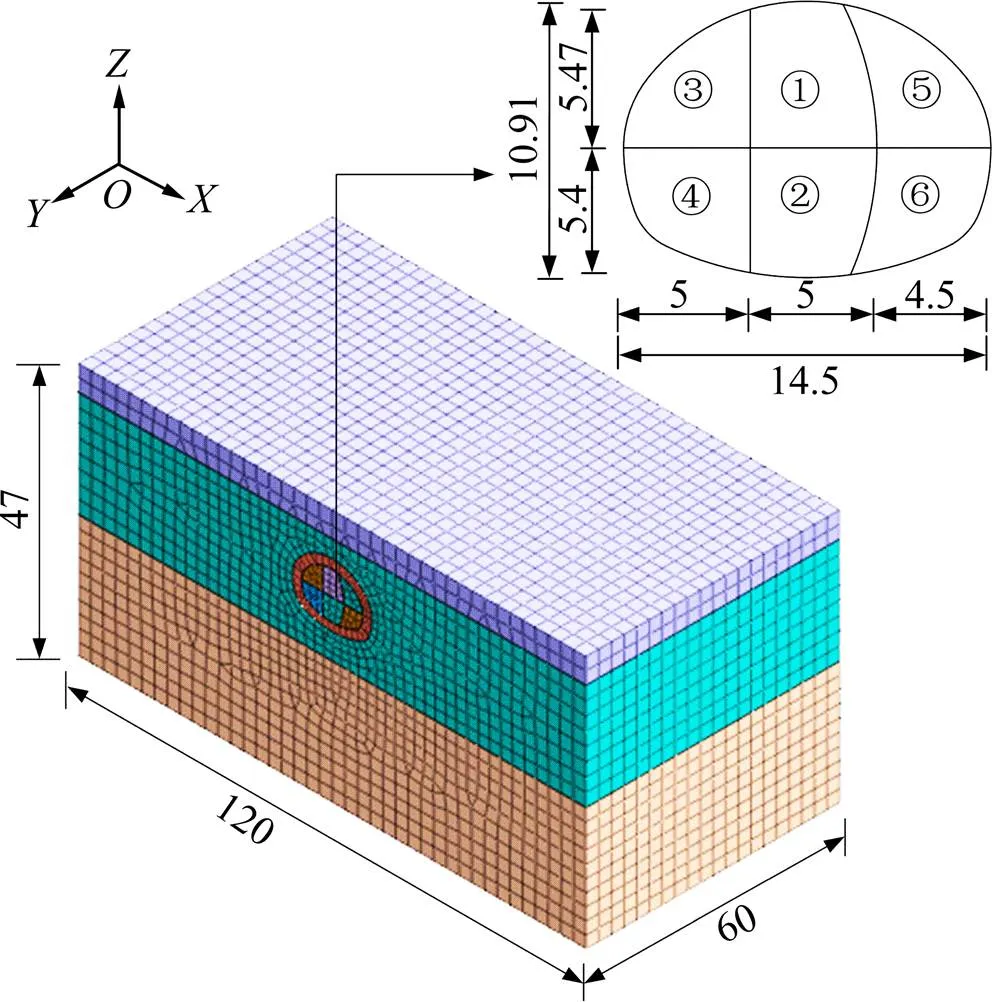
单位：m

文献[14−15]提出隧道施工工序能影响隧道稳定性；文献[3]提出初支封闭时间能影响隧道稳定性，然而施工步距和导洞错开距离均能影响隧道初支封闭时间，故把这施工步距与Ⅰ和Ⅱ部导洞错开距离作为影响隧道稳定性的因素；文献[2]提出在软弱围岩中加固方式和加固参数会影响隧道稳定性。加固区强度越高和范围越广，隧道施工稳定性越好，但其造价越高，因此本文把加固参数和加固范围进行组合，作为为同一个影响参数。本文把施工步距()，加固区强度()，加固区范围 ()，固定分区与动态分区错开距离()和施工工序()作为影响隧道稳定性的因素。如何调整这些施工参数，使隧道稳定性最好，是本文研究重点。因为固定分区Ⅰ部采用CRD法施工，动态分区Ⅱ部采用台阶法施工，但是每个导洞的施工顺序仍需讨论，1~4施工顺序均不同，如图2所示施工工序如下：1：1-2-3-4-5-6；2：3-4-1-2-5-6；3：5-6-1-2-3-4；4：5-6-3-4-1-2。

表1 材料参数

2.2 正交试验设计

在同一埋深和地质条件下，影响城市地铁浅埋暗挖大断面渐变隧道稳定性因素较多，本文通过广泛调研，认为，()，和等都能影响暗挖隧道稳定性，因此设计L16(4×4)正交表进行正交试验设计，见表2。

表2 主要影响因素及水平

2.3 试验方案与结果

由表3可知工况2的地表沉降最小为22.9 mm；工况1的围岩应力最小为0.78 MPa；工况14的拱腰水平位移最小为12.4 mm；工况5的右侧拱顶沉降最小为27.4 mm。1和2的整体结果均偏小，加固区范围0.5 m和强度500 MPa的计算结果均偏大。其他加固区组合结果均较小。+()对隧道的稳定性有很大影响；为10或15 m时和为1或2 m时结果均较小，因为初支快速封闭对隧道稳定性有促进作用。

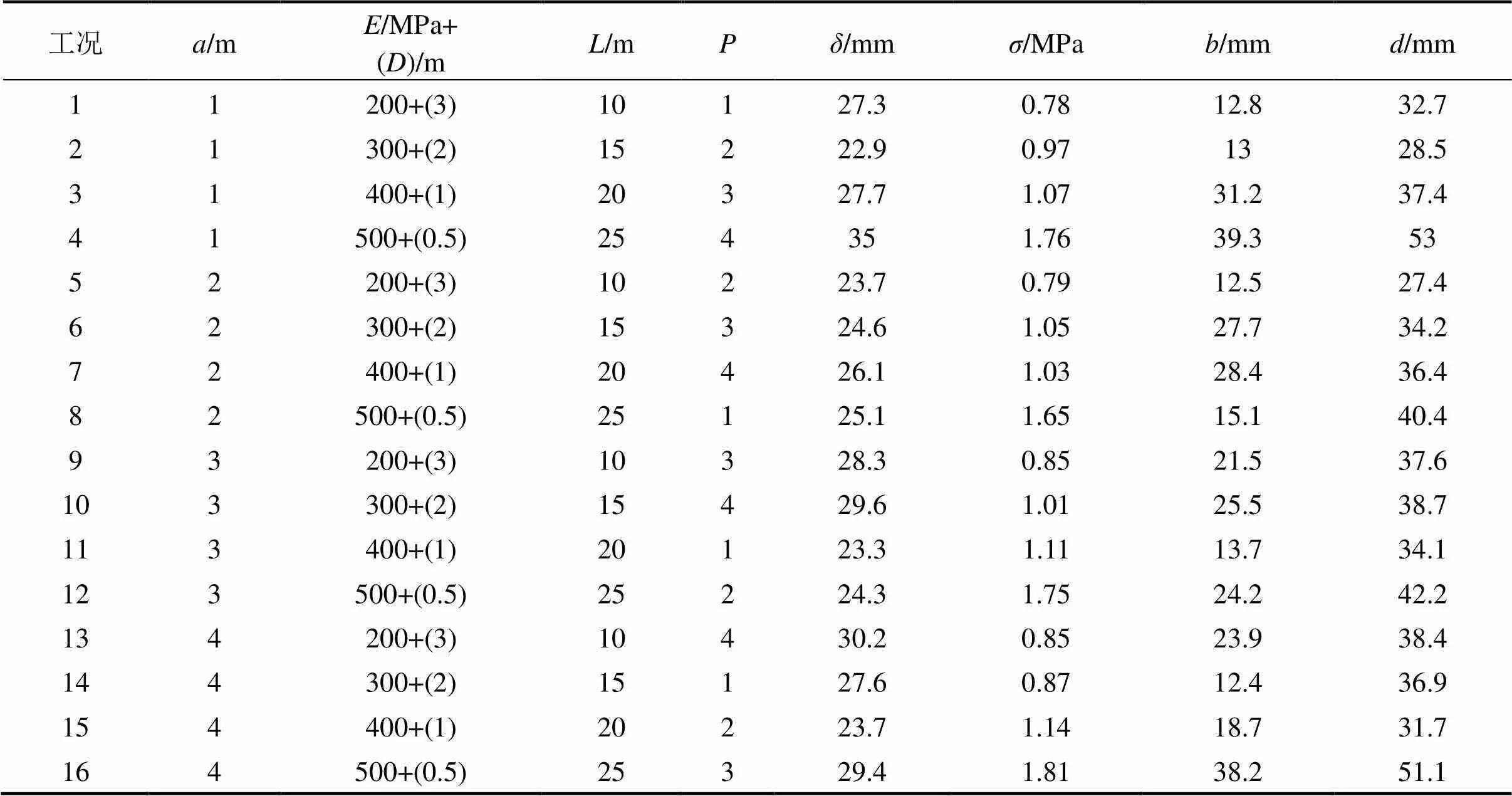
表3 正交试验方案和结果

注：代表最大地表沉降；代表围岩最大应力；代表拱腰水平位移；为右侧导洞拱顶沉降。

2.4 施工方案稳定性评估

采用模糊层次分析法计算主观权重，4个专家进行打分，综合求解主观权重，由于篇幅限制，仅列出一个专家打分，如表4所示。目标层(G)是隧道稳定性评估指标。因子层是最大表面沉降(F1)，最大围岩应力(F2)，拱腰水平位移(F3)和右拱顶最大沉降(F4)。评估因子如图4所示。

根据式(13)~(15)求得熵值法客观权重：

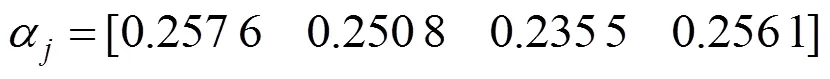
主观权重：

按式(16)计算组合权重：

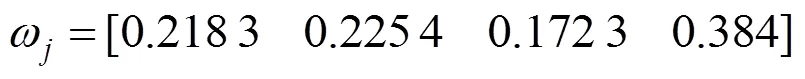
经组合赋权后，各指标权重大小依次为：右侧拱顶沉降＞围岩应力＞地表沉降＞拱腰水平位移。对表5中的评判指标进行归一化处理，并采用式(3)进行赋权得出C矩阵，如表4所示。其中理想解C+={0.218 3 0.225 4 0.172 3 0.384}，负理想解C−={0.142 8 0.097 1 0.054 4 0.198 5}，并通过式(6)~(7)确定理想解和负理想解的欧氏距离D+和D−，并对欧氏距离进行归一化处理如表5所示。

表4 G-C判断矩阵

表5 TOPSIS数据处理

将TOPSIS加权的矩阵和正、负理想方案通过式(8)~(9)求得正、负关联系数R和R，并进行归一化处理如表6所示。再根据式(10)~(12)求得S和S和相对贴近度，并根据大小进行排序，结果如表6所示。贴近度越接近1，方案越差，隧道稳定性越低，反之越接近0，方案越好，稳定性越高。由表6可知：工况5的贴近度为0.182 7，说明正交试验中工况5的方案为最优方案；其次是工况2，贴近度为0.311 8；工况16的贴近度为0.811 8，是本次试验中贴近度最低值的组合，故工况16组中最差的方案，隧道稳定性也最差。

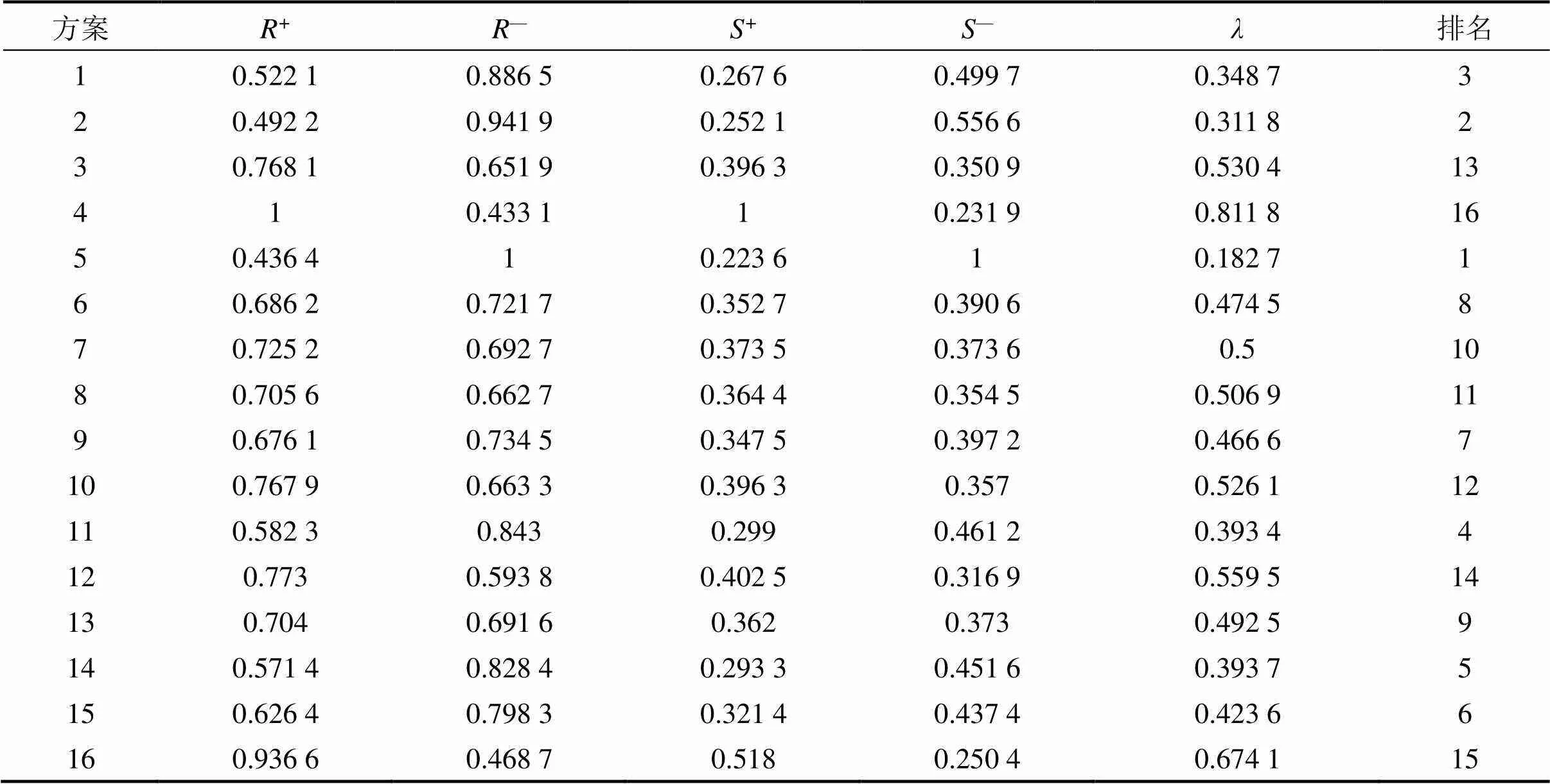
表6 相对贴近度计算

3 最优方案与结果分析

3.1 影响规律分析

利用主效应分析来研究隧道施工稳定性参数对地表沉降()，围岩应力()，拱腰水平位移()，右侧拱顶沉降()和相对贴近度()的影响规律。图5所示为，()和单独变化时的变化趋势，其中轴表示每个工艺参数的4个水平，轴表示每个响应的数值大小，虚线代表平均值。

由图5(a)可知，对于地表沉降，施工顺序对的影响最大，，+()和的影响较小。其中随着，+()，和增加，先减小后增大。要使地表沉降最小，和取水平2，+()和取水平3，即=2 m，=400 MPa，=1 m，=20 m，=2，称为min-参数组合。

由图5(b)可知，对于拱腰水平位移，+()、和的斜率都很大，表明三者对影响很大；而斜率较小，对的影响较小。随+()、和增大而增大；随增加，先减小后增大。要使拱腰水平位移最小，取水平2，+()、和取水平1，即=2 m，=200 MPa，=3 m，=10 m，=1，称为min-参数组合。

由图5(c)可知，对于围岩应力，+()和的斜率都很大，表明二者对影响很大；而和对的影响较小。随+()和增大而增大；随增加，在进行波动；随增加，先增加后减小，但幅度很小。要使围岩应力最小，取水平2，+()，和取水平1，即=2 m，=200 MPa，=3 m，=10 m，=1，称为min-参数组合。

由图5(d)可知，对于右侧拱顶沉降，+()和在水平1~3时，对影响很小；在水平4时，对影响较大。随和的增大，先减小后增大。要使右侧拱顶沉降最小，和取水平2，+()和取水平1，即=2 m，=200 MPa，=3 m，=10 m，=2，称为min-参数组合。

由图5(e)可知，对于相对贴近度，+()、和的斜率较大，表明三者对影响较大；而对的影响较小。随+()和增大而增大；随和增加，先减小后增大。因此要使贴近度最小，和取水平2，+()和应取水平1，即=2 m，=200 MPa，=3 m，=10 m，=2，称为min-参数组合，且最优方案为工况5。

根据上述分析，，，，和均为参数依赖性响应，施工参数对相对贴近度的影响程度是4个评价指标影响大小的加权和。因此施工参数对4个评价指标的影响可以通过相对贴近度的变化来体现。

3.2 多种方法对比分析

为了进一步说明本文采用的方法的准确性与先进性，另外采取2种方法对隧道的数据进行处理，其中由于篇幅原因，各方法不做具体说明。其中方法1采用传统灰色关联度法，计算权重为1/；方法2采用熵值法—灰色关联度计算灰色关联度，方案3为本文方法。各方法的灰色关联度计算结果如图6所示。

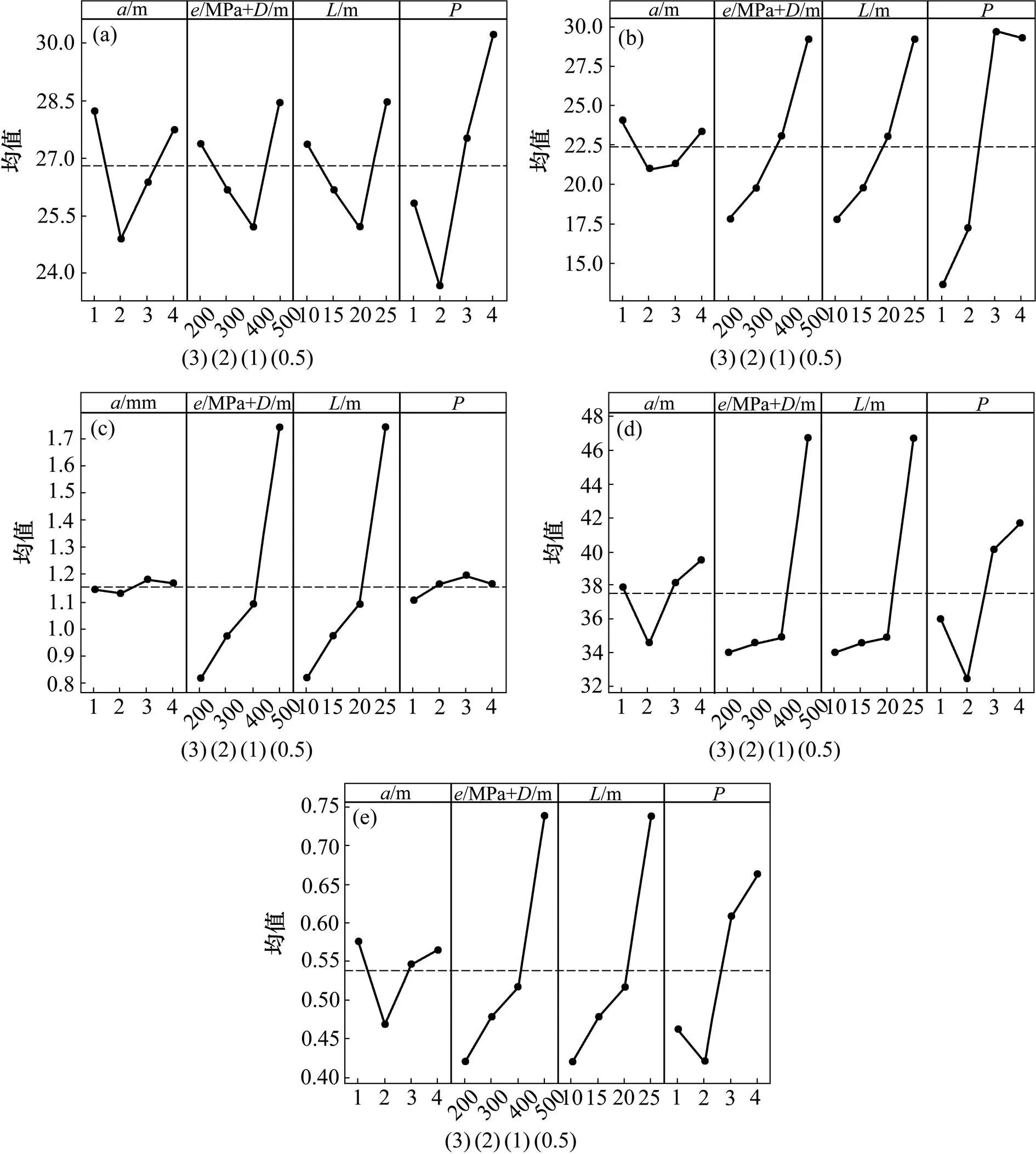
(a) 地表沉降(δ)主效应图；(b) 拱腰水平位移(b)主效应图； (c) 围岩应力(σ)主效应图；(d) 右侧拱顶沉降(d)主效应图；(e) 相对贴近度(λ)主效应图

从图6可知：方法1和方法2灰色关联度越大越优，方法3相对贴近度越小方案越优，故可知方法3和方法1的变化规律相反。方法3最小贴近度为0.182 7，而方法1最大灰色关联度为0.960 3，方法2的灰色关联度为0.959 8，最优方案均为方案5，验证了本文方法的准确性。从图中可知方法1和方法2几乎没有差别，因为熵值法计算各评价指标的权重大致相同，和方法1的权重系数1/计算结果大致相同。但是方法1传统灰色关联度默认所有指标权重相同，导致精确度不高，只能粗略的得出最优方案，当各方案差距较小时，会出现灰色关联度相同的方案，难以抉择，方法2与方法1类似。

本文方法将熵值法和层次分析法进行结合，形成组合赋权，将定性分析和定量分析有效结合计算权重，采用灰色关联度对TOPSIS进行改进。将组合赋权、欧氏距离和灰色关联度相结合，使评价结果更加合理。

图6 各种方法对比分析

3.3 施工沉降分析

从图6和min-可知最优方案是工况5，并将最优方案用于北京地铁17号线天通苑站，固定分区Ⅰ部平均每天掘进1 m，待固定分区Ⅰ部掘进10 m后，开始施工动态分区Ⅱ部，动态分区Ⅱ部每天掘进1.5 m。施工现场如图7所示。

图7 固定分区Ⅰ-3部施工现场图

施工监测地表沉降最大值为−25.1 mm，比模拟结果大5.9%，但小于规范规定30 mm，满足要求。因为施工现场经常出现钢拱架支撑不及时；加固区范围和强度未达标；超挖等现象造成施工结果偏大。但施工监测和最优方案模拟结果相差甚小，既能证明本文方法的准确性，更加能证明本文方法的先进性。

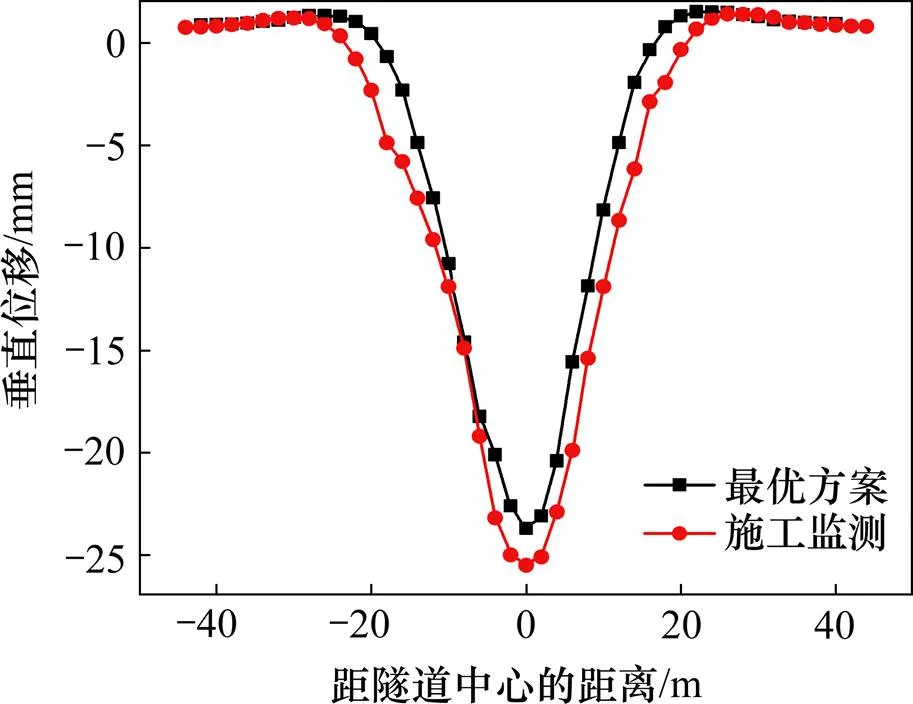
图8 施工监测和最优方案地表沉降对比分析

4 结论

1)本文采用的改进TOPSIS法研究浅埋暗挖大断面隧道稳定性的影响因素，从min-可知：隧道施工工序、加固区强度和范围、Ⅰ及Ⅱ部导洞错开距离对隧道整体稳定性的影响较大，施工步距对隧道整体稳定性的影响较小。

2) 本文方法与其他2种方法对比分析，验证了本方法的准确性，组合权重通过熵值法对数据进行客观处理，更加真实可靠，再通过层次分析法对评价指标进行主观分析，增强其逻辑性，最后得出的权重更加真实可靠。组合赋权和灰色关联度对TOPSIS进改进，将组合赋权、欧氏距离和灰色关联度相结合，使评价结果更加合理。

3) 本文方法当评价指标类型和数据较少时更为适用，特别是在各方案差距较小时，很少出现相对贴近度相同的方案，计算精度更高，更容易凸显最优方案，这也是本方法的先进性。

[1] 严金秀. 中国隧道工程技术发展40年[J]. 隧道建设(中英文), 2019, 39(4): 523−536. YAN Jinxiu. Development of tunnel engineering technology in China for 40 years[J]. Tunnel Construction, 2019, 39(4): 523 −536.

[2] 来弘鹏, 康佐, 谢永利, 等. 地铁区间隧道黄土地层注浆预加固技术研究[J]. 中国铁道科学, 2014, 35(1): 47−54. LAI Hongpeng, KANG Zuo, XIE Yongli, et al. Grouting pre-reinforcement technology for metro tunnel in loess strata[J]. China Railway Science, 2014, 35(1): 47−54.

[3] FANG Qian, ZHANG Dingli, Louis Ngai Yuen Wong. Shallow tunnelling method (STM) for subway station construction in soft ground[J]. Tunnelling and Underground Space Technology, 2012, 29(5): 10−30.

[4] XUE Yiguo, ZHANG Xueliang, LI Shucai, et al. Analysis of factors influencing tunnel deformation in loess deposits by data mining: A deformation prediction model[J]. Engineering Geology, 2018, 232(8): 94−103.

[5] 吴波. 复杂条件下城市地铁隧道施工地表沉降研究 [D]. 成都: 西南交通大学, 2003. WU Bo. Study on ground subsidence of metro tunnel construction under complex conditions[D]. Chengdu: Southwest Jiaotong University, 2003.

[6] 王新民, 秦健春, 张钦礼, 等. 基于AHP-TOPSIS评判模型的姑山驻留矿采矿方法优选[J]. 中南大学学报(自然科学版), 2013, 44(3): 1131−1137. WANG Xinmin, QIN Jianchun, ZHANG Qinli, et al. Mining method optimization of Gu Mountain stay ore based on AHP-TOPSIS evaluation model[J]. Journal of Central South University (Science and Technology), 2013, 44(3): 1131−1137.

[7] 邬晓光, 贺攀, 苏兴矩, 等. 基于海明距离-TOPSIS法的山区公路隧道扩建方案直觉模糊优选[J]. 隧道建设, 2017, 37(8): 926−932. WU Xiaoguang, HE Pan, SU Xingju, et al. Intuitionistic fuzzy optimization of enlargement scheme of highway tunnel in mountain areas based on hamming distance-TOPSIS method[J]. Tunnel Construction, 2017, 37(8): 926−932.

[8] SUN W, LI D, LIU P. A decision-making method for sponge city design based on grey correlation degree and TOPSIS method[J]. Journal of Interdisciplinary Mathematics, 2018(21): 1031−1042.

[9] Tajvidi Asr E, Hayaty M. Selection of optimum tunnel support system using aggregated ranking of SAW, TOPSIS and LA methods[J]. International Journal of Applied Operational Research, 2015(5): 49−63.

[10] ZHAN K, YUAN Y P, SUN L L, et al. Optimal solar energy guarantee rate of hot water system based on grey correlation improved TOPSIS method[J]. Journal of Solar Energy, 2016(37): 1218−1226.

[11] 邱自学, 鞠家全, 任东, 等. 基于正交试验、组合赋权−灰色关联的机床横梁优化设计[J]. 振动与冲击, 2017, 36(12): 105−111. QIU Zixue, JU Jiaquan, REN Dong, et al. Optimization design for the crossbeam of a machining tool based on the orthogonal experimental method and combination weight-grey relational analysis[J]. Journal of Vibration and Shock, 2017, 36(12): 105−111.

[12] 康立鹏, 施成华, 彭立敏, 等. 基于正交试验的立体交叉隧道施工影响因素研究[J]. 铁道科学与工程学报, 2012, 9(4): 70−74. KANG Lipeng, SHI Chenghua, PENG Limin, et al. Influencing factors of three-dimensional intersection tunnel construction based on orthogonal test[J]. Journal of Railway Science and Engineering, 2012, 9(4): 70− 74.

[13] 赵挺生, 任玲玲, 周炜, 等. 基于熵权法-CIM模型的高速公路施工临近房屋安全风险评价[J]. 中国安全生产科学技术, 2017, 13(3): 174−179. ZHAO Tingsheng, REN Lingling, ZHOU Wei, et al. Safety risk assessment on buildings adjacent to construction site of expressway based on entropy- weight method and CIM model[J]. Journal of Safety Science and Technology, 2017, 13(3): 174−179.

[14] Ki-Chang Hyun,Sangyoon Min,Hangseok Choi, et al. Risk analysis using fault-tree analysis (FTA) and analytic hierarchy process (AHP) applicable to shield TBM tunnels[J]. Tunnelling and Underground Space Technology, 2015(49): 121−129.

[15] KE Wu, YU Yalin, CUI Shuaishuai, et al. Construction mechanical mechanism of shallow subway tunnel group with large-span variable cross section[J]. Geotechnical and Geological Engineering, 2018(36): 3879−3891.

Study on tunnel construction scheme optimization based on improved TOPSIS method

WU Bo1, 2, LU Ming1, 2, LEI ling3, HUANG Wei1, 2, HUANG Zonghui1, 2

(1. College of Civil Engineering, Guangxi University, Nanning 530004, China; 2. Key Laboratory of Engineering Disaster Prevention and Structural Safety Ministry of Education, Guangxi University, Nanning 530004, China;3. Zhongjiao Road and Bridge Engineering Bureau Co., Ltd, Beijing 101116, China)

Due to the harsh environment around the city subway, poor geological conditions, and difficult to ensure the stability of the tunnel, a reasonable choice of tunnel construction plan is a prerequisite for successful completion. Taking into account the objective environment and manual operation factors, the excavation sequence, the initial support closure time, the reinforcement range and parameters are selected as the main factors affecting the stability of the tunnel, and the L16(4×4) orthogonal table is constructed according to the influencing factors. The test was carried out and the test plan was numerically simulated. Finally, based on the tunnel convergence deformation and surrounding rock stress as the evaluation index, an improved TOPSIS evaluation model was established, and the optimal scheme was applied to the Tiantongyuan Station project of Beijing Metro Line 17. The research results show that the relative closeness of working condition 5 is the lowest, its value is 0.182 7, so working condition 5 is the optimal solution; the optimal solution is 5.9% smaller than the actual engineering surface settlement, indicating that the improved TOPSIS method can be widely applied to shallow burial. The optimization of the method of excavating large-section tunnels is also useful for intricate tunnel engineering.

tunnel engineering; optimal scheme; improvement of TOPSIS; shallow buried tunnel; orthogonal experiment

U459.3

A

1672 − 7029(2020)06 − 1471− 09

10.19713/j.cnki.43−1423/u.T20190691

2019−08−01

国家自然科学基金资助项目(51478118，51678164)；广西特聘专家专项资金资助项目(20161103)；广西自然科学基金资助项目(2018GXNSFDA138009)；广西科技计划资助项目(AD18126011)

吴波(1971−)，男，四川阆中人，教授，博士，从事地下空间和隧道工程研究；E−mail：813792833@qq.com

(编辑 蒋学东)