柱状茭白真空预冷热质传递分析

王 宁，阚安康*，黄孜沛，陆家希，潘雨芹

（上海海事大学商船学院，上海 201306）

真空预冷是食品保鲜的重要技术之一，也是冷链物流过程中重要的支撑技术，与其他冷却方法相比其冷却时间十分短暂，有着明显的优势[1-6]。其原理是真空条件可使材料中水分快速蒸发，蒸发的水蒸气带走材料潜热并向外界释放，从而达到使材料迅速降温的目的[7-9]。在真空预冷过程中，食品温度分布和失水率一直是业界关注的问题。温度分布不均可能导致低温损伤，对食品品质产生一定负面影响，进而导致经济损失[10]。数学模型是有效的模拟工具，可以用来从理论上描述真空预冷过程，有利于改进设备、优化工艺和控制产品品质[11-13]；针对肉类、蔬菜和木材等不同材料真空预冷过程的模拟，国内外学者已建立了众多数学模型，用于预测系统压力、温度和产品失水率等各种参数。Torres等[14]提出了一种理想固体多孔介质真空干燥模型的数值求解方法，研究介质内部水蒸气和空气的动力变化情况。Salehi等[15]建立真空干燥数学模型，研究了红外-真空联合干燥对柠檬片的干燥动力学、水分扩散性、表面收缩和颜色变化的影响。结果表明，数学模型和实验结果较为吻合。金听祥等[16]为研究肉类在真空冷却中的温度分布和压力的变化情况，建立圆柱形肉块水分迁移的真空冷却数值模型，结果表明模拟结果和实验数据基本一致，温度最大误差在5%以内。Bahrani等[17]建立了淀粉材料真空降压过程中热质传递的物理模型，解释了淀粉加工过程中热量和质量传递的变化机理。Sun Dawen等[18]使用计算流体软件建立了多孔材料真空冷却的非稳态数值模型，并通过多孔食品数值模拟和实验结果的对比，成功验证了真空冷却过程中多孔食品的热质传递。Drummond等[19]对熟牛肉浸泡式真空冷却过程建立了数学模型，研究牛肉尺寸、孔隙率大小与工艺参数对熟牛肉样品在真空冷却期间的冷却时间、总质量损失、压力和温度分布的影响，并成功进行了模型验证。贺素艳等[20]对甘蓝真空预冷过程进行了理论模拟，考虑装置泄漏面积，通过实验计算出了甘蓝实际传质系数，这为其他真空预冷系统的泄漏面积计算提供了新方法。王雪芹等[21]以卷心菜为研究对象，建立了真空冷却过程中球形果蔬的非稳态传热传质模型，并考虑了蒸发、对流和辐射等因素对温降的影响，同时通过实验成功验证了模型的准确性。韩志等[22]提出了真空预冷过程中球形食品的传热模型，并利用UDF自定义编程，引入食品材料的物性参数，使用FLUENT软件对食品真空预冷过程进行了数值模拟。阚安康[23]、陈雪梅[24]等建立了多孔蔬菜真空预冷传热传质数值模型，通过模拟数据和实验结果的对比，验证了柱状蔬菜降温速率和质量损失变化情况。He Zhenbin等[25]建立了木材真空干燥过程中各时间点的热质耦合传递模型，并对模型进行了验证，结果表明，水分含量高于纤维饱和点木材的平均干燥速率约为水分含量低于纤维饱和点木材的2.91 倍。Demarchi等[26]建立了玫瑰果皮真空干燥过程中水分、温度和抗坏血酸含量的变化模型，对热量和质量损失进行了较好的预测。Song Xiaoyan等[27]利用数学模型模拟真空预冷中切叶蔬菜的传热过程，并对鲜切青菜真空预冷时的表面温度分布及其叶部和叶柄的平均表面温度进行了预测，在红外热成像技术的帮助下，通过理论和实验数据的对比，成功地验证了数学模型。

茭白味道鲜美、营养价值高，但其含水率高达90%以上，易腐烂变质，货架期短[28]。为解决茭白保鲜问题，在流入消费市场前，可以对茭白进行真空预冷处理。然而真空条件下蔬菜失水的现象不可避免，真空预冷会对茭白品质产生影响。因此，本实验从理论上分析真空下柱状蔬菜热质传递的过程，并以柱状茭白为研究对象，建立柱状茭白热质传递数值模型，通过实验数据与模拟结果对比来检验模型的准确性，这对茭白保鲜和延长茭白市场货架期具有一定的理论和指导意义，同时也为同类柱状蔬菜在真空预冷保鲜过程中提供相应借鉴。

1 材料与方法

1.1 材料

新鲜茭白为市售。

1.2 仪器与设备

ZLG0.1A型真空预冷试验机 上海善如水保鲜科技有限公司；HZY-B1000电子天平 福州华志科学仪器有限公司。

真空预冷装置系统如图1所示，主要由真空泵和压缩机组成，通过配备T型热电偶和压力传感器的数据采集系统，对蔬菜内部温湿度和真空室内压力进行连续测量和采集。真空室内尺寸500 mm×410 mm×490 mm；最低真空度为400 Pa，显示精度为1 Pa；预冷最低温度-5 ℃，在-5～40 ℃之间可任意设定，显示精度0.1 ℃，相对湿度传感器精度0.5%。

图1 真空预冷系统图Fig. 1 Schematic diagram of the vacuum cooling device

1.3 方法

1.3.1 热质传递模型的建立

真空预冷过程主要分为3 个阶段。第一阶段是恒温和降压阶段，在此阶段样品温度基本不变，真空室内压力逐渐下降。当压力下降到材料初始温度对应的饱和压力（闪点）时，材料中的自由水开始吸热蒸发，材料即迅速降温，降温效果明显，此为真空预冷的第二阶段。随着水分的不断蒸发和向外排放，材料温度将迅速下降到设定的温度工况。第三阶段是压力恢复阶段，此阶段预冷装置进气阀打开，外界空气流入真空室内直至内外压力平衡[29]。综上，主要的热质传递发生在第二阶段，故本研究的热质传递模型就是基于这一阶段所建立。

多孔材料真空预冷中的各部位压强条件和汽化强度是相同的，其温降速率亦相同；在真空预冷过程中，热量传递的方式有相变热（即材料水分蒸发吸收的热量）、热传导（即材料内部的导热）、对流传热（即材料外表面与真空室内气体、腔体内壁的热交换）、辐射热（即真空室内材料与气体、腔体内壁之间的换热量）。辐射换热量与材料自身温度、黑度和辐射系数有关，在本实验模拟中热量小，可被忽略。

为了简化计算，在建立柱状茭白数学模型时作如下假设：1）真空预冷装置密闭性好，不考虑外界空气的渗透；2）辐射换热量少，忽略不计；3）模型初始温度和水分含量分布均匀，模拟过程中材料的热物性参数恒定不变且各向同性；4）材料吸热产生的水蒸气完全被捕水器捕获。

1.3.1.1 传热模型

根据以上假设条件，茭白真空预冷过程的非稳态传热控制方程可用公式（1）表示。考虑到新鲜的茭白是一个有机生命体，进行的呼吸作用会产生呼吸热，故传热过程涉及的内热源可由公式（2）表示。

式中：ρf为茭白密度/（kg/m3）；cp为茭白比热容/（kJ/（kg·K））；λ为茭白导热系数/（W/（m·K））；T为温度/K；t为时间/s；x、r、θ分别为柱坐标系；φ为内热源/（kJ/kg），由蒸发潜热和呼吸热两部分组成；hfg为水的汽化潜热/（kJ/kg）；fv为茭白中水蒸气的产生速率/（kg/（m·s））；fbh为茭白自身的呼吸热/（kJ/（m·s））。

根据公式（3）～（5）确定内热源。

式中：ε为茭白的孔隙率；M为相对分子质量；R0为通用气体常数，取为8.314 J/（mol·K）；da为多孔介质的茭白孔径/m；μ为水蒸气的动力黏度/（kPa·s）；P为真空室内环境压力/Pa；ξx、ξr和ξθ分别为x、r、θ所对应的水蒸气迁移阻力因子。

1.3.1.2 传质模型

真空预冷过程中水分达到闪点后，将从茭白内部吸热蒸发，茭白单位体积的蒸发速率可用公式（6）[16]表示。

式中：D为茭白的直径/m；hm为茭白的沸腾系数，取为8.4×10-7kg/（Pa·m2·s）；Ps为茭白在温度T下对应的饱和压力/Pa；Pv为真空室内的压力/Pa。

Ps与茭白温度T的关系可用公式（7）表示。

真空室内压力Pv随时间的变化关系用公式（8）表示。

式中：S表示真空泵的抽气速率/（m3/s）；Vf表示真空室的容积/m3。

1.3.1.3 初始条件和边界条件

初始条件如式（9）所示。

式中：T0为茭白初始温度/K；P0为茭白所处的真空室内初始压力/Pa。

边界条件如式（10）所示。

式中：ω为茭白真空预冷产生的水蒸气质量分数/%。

茭白表面边界条件如式（11）所示。

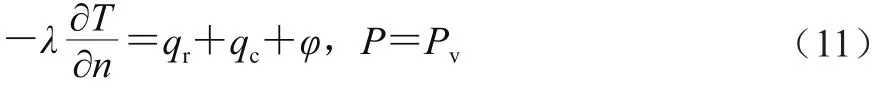
式中：n、qr和qc分别表示茭白的表面法向量、辐射热和对流换热/（kJ/kg），其中数值求解时辐射热和对流换热可忽略，即qr＝0，qc＝0。

1.3.1.4 茭白的热物性参数

茭白的导热系数按照公式（12）[30]求取。

式中：ωw、ωp、ωc、ωf和ωa分别表示茭白中水分、蛋白质、碳水化合物、脂肪和灰分的质量分数/%。

茭白的比热容按照公式（13）[30]求取。

实验中孔隙率取0.63，茭白多孔介质的平均孔径取0.002 5 m[18]，其他指标参数值如表1所示，其中，茭白质量由电子天平测定；各成分质量分数委托上海海洋大学食品学院实验测定；直径由直尺测量；密度由质量与体积比求平均值；初始温度、初始压力由真空预冷设备自带传感器测定。将各数据代入FLUENT软件求解。

表1 真空预冷过程中的水分迁移模型参数Table 1 Model parameters for moisture migration during vacuum cooling

1.3.2 验证实验

1）将购买的茭白进行筛选，选择半径2 cm、长18 cm的茭白适当去皮并称质量，确保其几何大小与模型尺寸参数一致。2）将温度传感器的两个探头分别插进茭白中心、表面位置（图2A）；茭白样品初始温度为24 ℃，最终温度设置为2 ℃。3）启动设备，制冷机和真空泵同时运行，直至茭白中心处最终温度达到设定值，系统每隔10 s自动采集压力、温度及相对湿度等数据并记录。4）重复1～3过程。5）实验测试工作结束，关闭实验系统。

图2 茭白的测试点位置及装置Fig. 2 Test locations and equipment for Zizania latifolia

2 结果与分析

2.1 模型网格划分

真空预冷中的材料温度和压力都是随时间而不断变化的，因此这是一个非稳态过程。本实验中柱状模型使用隐式差分法来求解茭白真空预冷中的热质传递微分方程。首先划分网格，建立x、r、θ柱坐标系，再将计算区域和时间坐标分别均匀划分为（a-1）、（b-1）份，因此空间节点为a个（1≤a≤A），而时间节点b（0≤b≤n）可由n×Δi表示，Δi为时间间隔。模型中a＝0位置为茭白的中心，令其为第一节点，茭白表面为最大节点A。基于能量守恒定律、质量守恒定律以及提出的柱状数学模型，针对茭白内某一微元体Δr/2（△r为空间两相邻节点的距离）处的热质平衡，可得茭白内部节点的有限差分方程，如式（14）所示。

式中：Tab＋1和Tab分别表示同一个空间节点在两相邻时间下的温度/K；Tab和Tba-1分别表示在相同时间下的相邻空间节点的温度/K；Δr为空间两相邻的节点距离。

在r＝0，即a＝0时，茭白中心节点的差分方程如式（15）所示。

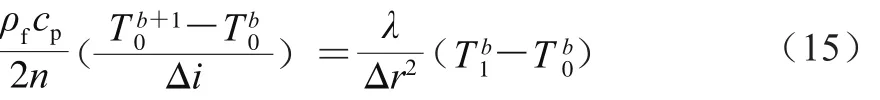
式中：T0b＋1和T0b分别表示中心节点在两相邻时间下的温度/K；T1b和T0b分别表示在相同时间下的中心及其相邻空间节点的温度/K。

在r＝R，即a＝A时，茭白表面节点的差分方程如式（16）所示。

式中：Rw为水的气体常数/（J/kg）；D0为在温度273 K下一个标准大气压下水蒸气在空气中的扩散系数（0.22×104m2/s）；l为传质阻力层厚度/m；Paw为真空室内环境水蒸气分压/Pa；aw为水分活度。

基于上述数学模型分析，建立茭白柱状数值模型，ICEM-CFD（the integrated computer engineering and manufacturing code for computational fluid dynamics）网格划分如图3所示。通过FLUENT软件，根据上述各参数的设置，对柱状蔬菜的真空预冷过程进行模拟求解。

图3 柱状模型网格划分Fig. 3 Cylinder model meshing

2.2 模拟茭白温度变化

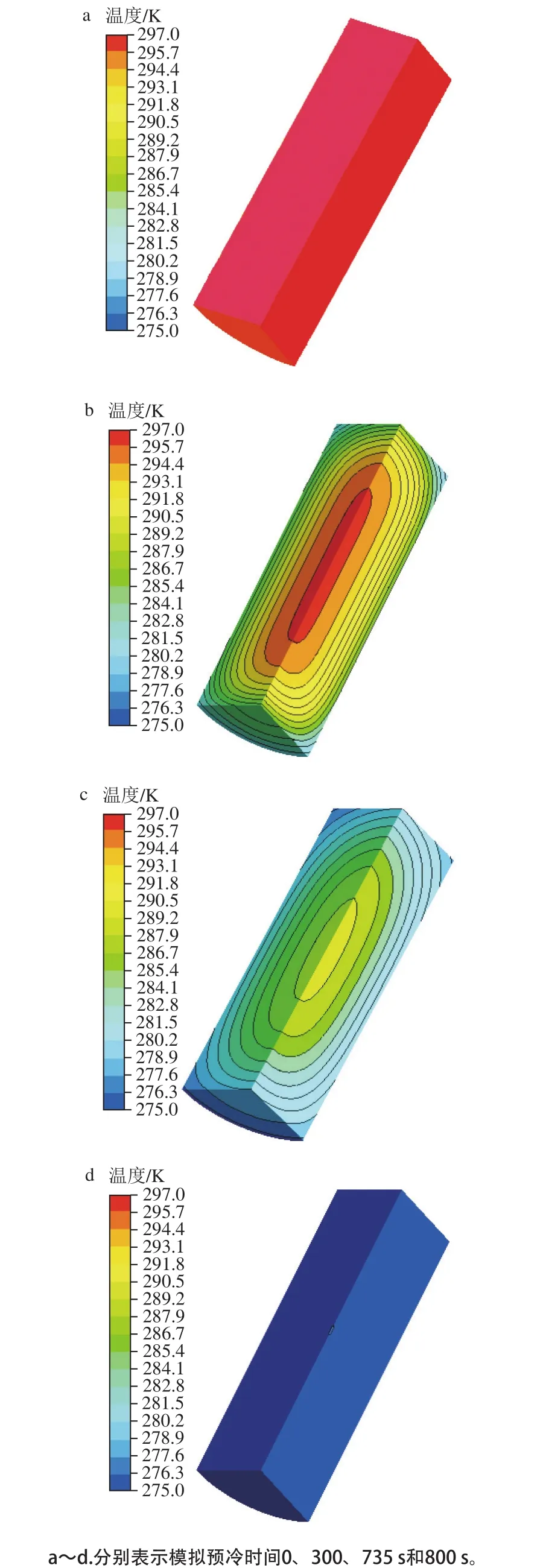
图4 茭白真空预冷后的内部温度云图Fig. 4 Temperature profiles inside Zizania latifolia after vacuum cooling

真空预冷过程中茭白横向和纵向切面的温度变化云图如图4所示。在模拟初始时刻（0 s），茭白的起始温度为297 K，此时预冷设备未启动，茭白温度与真空室内环境之间没有温度差，故茭白温度保持不变。当进行300 s后，在真空泵的抽吸作用下，真空室内气体被连续排除，茭白外表面与环境之间发生强制对流，室内压力和流体温度也因此降低；当茭白表面温度达到其压力对应饱和水的蒸发温度时（闪点），茭白外层水分开始吸热蒸发，其温度由内到外依次迅速降低，从图4b能够看出茭白的温度分布是以芯部为中心的圆弧圈。随着模拟的进行，茭白外表面温度在735 s时最先到达设定值（275 K），此时茭白芯部温度在内外温差驱动下主要依赖导热缓慢下降，这是因为茭白外层水分的闪发，使得整个茭白周围充满水蒸气，即增加了茭白内层水分的闪发阻力。在真空泵的持续抽吸作用下，真空室内的水蒸气不断被排出，茭白内层水分在压力差的驱动下向外层迁移，同时伴随着吸热蒸发，导致茭白芯部的温度也迅速降低。800 s时，柱状茭白真空预冷热质传递过程模拟结束，茭白停止吸热蒸发，其外表面和内部温度基本相同。

2.3 真空室内压力和温度变化验证实验结果

图5 茭白压力和温度模拟值与实验值的对比Fig. 5 Comparison of simulated and experimental values for pressure in the vacuum chamber and internal and surface temperature of Zizania latifolia

真空预冷过程中实验数据和模拟数据的压力变化曲线如图5a所示。在真空预冷初始阶段，真空室内的模拟压力与实验压力均以较高的压降速率下降，但前者数值稍低；在预冷中期，茭白内部水分到达闪点后吸热蒸发，真空室内压降放缓，到预冷后期两者曲线基本吻合并保持水平不变。这是因为模拟真空预冷过程的真空泵功率是维持不变的平均功率，因此，在降压初始阶段，真空泵工作效率高，抽气速率快，降压速率高，且不考虑外界空气的渗入；然而在验证实验过程中，真空泵的初始功率低，真空室内压力下降速率较小，而且外界的空气会向真空室内渗透，抽气速率也相对较慢。随着真空泵的连续工作，验证实验中的真空泵功率趋于恒定，200 s后模拟值和实验值的压力误差逐渐缩小，最大偏差不超过100 Pa。真空预冷过程结束时，室内压力均保持恒定不变，模拟压力为635 Pa，实验压力为686 Pa，模拟与实验压力误差仅为7.4%，两者压力变化曲线基本吻合。

茭白表面和中心位置的温度模拟数据与实验数据的曲线变化如图5b所示。在预冷初始阶段，真空室内空气被真空泵连续抽吸并向外排出，室内压力持续下降，直至达到茭白内部水分闪点，这一阶段主要是茭白与真空室内的空气发生对流换热，换热量微弱，茭白温度几乎没有下降。随后达到闪点的茭白外层水分在压力差作用下最先吸热蒸发，温度急剧下降，而这时茭白内层主要依赖导热降温。随着预冷过程的进行，茭白温度不断下降，当达到设定工况时，其内外层温度基本相同。真空预冷过程结束时，茭白终点处中心温度实验值比模拟值高，表面温度实验值比模拟值低，但茭白内外平均温度的模拟值要比实验值偏高，两者在整个真空预冷过程的最大误差仅为3.7%，这是因为验证实验所用的茭白都是经过机械鲜切处理的，这种机械损伤既破坏了茭白的组织结构，又改变了茭白内部水分迁移的通透性；因此，在真空预冷时，实验中的茭白水分更易流失，温度下降也更快。

2.4 真空室内质量损失和相对湿度变化验证实验结果

图6 茭白质量（a）和相对湿度（b）模拟值与实验值的对比Fig. 6 Comparison of simulated and experimental values for mass (a)and relative humidity (b) inside Zizania latifolia

构成蔬菜组织结构的水分包括结合水和自由水，结合水是指通过化学键与溶质分子、非水组织牢固结合的一类水，因此，在真空预冷过程出现损耗的水都是蔬菜组织结构和细胞中可以自由移动的自由水。在预冷过程中，茭白内部水分（自由水）达到闪点时会大量吸热蒸发并向外界排出，因此茭白的质量也会降低。如图6a所示，在真空预冷前期，验证实验与模拟茭白质量损失误差在1%以内；但在真空预冷后期，两者质量误差逐渐增大。真空预冷过程结束时验证实验茭白质量损失为6.3%，而模拟数据显示的质量损失为5.8%，两者间的误差仅为7.9%。一方面，是由于茭白在预冷实验中期达到闪点后内部水分大量吸热蒸发，蒸发的水蒸气包围整个茭白，阻碍了水分进一步的蒸发损失；另一方面，到实验后期，真空泵的连续抽吸使得真空室内气体被迅速排至外界，在压力差驱动下，外层水分的蒸发增加了茭白中的孔隙数量，结果内层水分向外转移能力得到提升的同时也能顺利吸热蒸发。

如图6b所示，在预冷起步阶段，茭白所处环境的相对湿度为66%，在预冷230 s时，真空室内相对湿度第一次达到最低值（24%）；而在220～400 s，真空室内相对湿度出现上升的态势并达到41%；400 s以后相对湿度又开始缓慢降低，第800秒时，真空室内相对湿度第二次达到最低值（19%），随后相对湿度维持不变。这是因为预冷初期真空室内气体被真空泵迅速抽吸排至外界，此时茭白的内部水分尚未达到闪点，真空室内相对湿度也因此第一次迅速到达最低点；随着预冷过程的进行，茭白内部水分在230 s后到达闪点，水分吸热快速蒸发，大量水蒸气包围茭白附近区域，使得真空室内水蒸气分压力升高，相对湿度也随之上升；随着水蒸气的生成与排出，茭白内外层的自由水含量也不断减少，所以400 s后真空室内相对湿度又开始缓慢下降；800 s后茭白内部水分基本完全蒸发，茭白温度达到设定值，室内相对湿度也第二次达到最低点并维持不变。

2.5 误差分析

该数学模型能有效模拟柱状茭白热质传递过程，但此模型存在误差，主要原因有：1）实验所用的茭白都是经过机械鲜切处理的，而且实验中热电偶需要插孔，这些无疑破坏了茭白的组织结构，进而对实验数据产生影响。2）由于茭白的上下端、内外部的密度和形态各有差异，因此对于建立的柱状数值模型，茭白难以真正实现物质分布均匀，整体一致。

3 结 论

本实验以茭白为柱状蔬菜的典型代表，建立了真空预冷热质传递模型，并分析了柱状茭白真空预冷实验的真空室内压力、相对湿度和茭白温度分布以及质量损失的情况，通过模拟和验证实验数据的对比，成功验证了数学模型。模拟与验证实验结果表明：1）在真空预冷初始阶段，真空室内降压速率快，模拟压力比实验压力稍低，茭白与真空室内空气温度基本相同，对流换热微弱，茭白温度变化不明显；茭白水分到达闪点后吸热蒸发，真空室内压降放缓，而降温速率增加；真空预冷过程中，茭白外表面部分降温速率高于中心处部分，模拟与验证实验结果中压力和温度变化曲线基本吻合。2）在真空预冷过程中，受真空室内水蒸气分压影响，相对湿度出现两次最低值，第一次在闪点之前，为24%，第二次在闪点之后，为19%。3）在真空预冷初期，模拟质量损失数据和验证实验数据相差不明显，误差在1%以内；真空预冷结束时，真空室内压力模拟值为635 Pa，实验值为686 Pa，模拟数值与实验数值误差仅为7.4%；温度模拟值与实验值的最大平均温度误差仅为3.7%。实验结果的质量损失为6.3%，模拟结果的质量损失为5.8%，两者误差在8%以内。