基于多目标决策的轨道控制网网形设计
宋占峰,杨 飞,李 军
(中南大学 土木工程学院,湖南 长沙 410075)
根据有砟铁路轨道精调和养护的要求,TB 10101—2018《铁路工程测量规范》增加了新建有砟轨道铁路CPⅢ控制网采用自由测站方式测设的技术标准:对于设计速度160~200 km/h之间的有砟铁路,CPⅢ网形为50~70 m一对点的边角交会网,点位中误差在3 mm内,相邻点的相对点位中误差在1.5 mm内[1]。
我国速度120 km/m以上铁路既有线里程已超过2万km。在长期运营中,既有线轨道的几何形状、空间位置不断发生改变,造成的轨道不平顺会影响列车的运行舒适度和安全性。因此,建立既有线轨道CPⅢ网,是既有铁路轨道精调和养护的迫切需求。
既有线上建立轨道CPⅢ网,不同于新建铁路:(1)天窗时间短,干扰大;(2)经费有限。因此,需要设计适合既有线的轨道CPⅢ网形。控制网设计中,网形的设计称为一类设计问题[2-3]。控制网设计质量的优劣取决于精度、可靠性和建网费用三个方面[4]。将既有线两侧的接触网支柱作为固定桩,布设控制点,可以减少建设费用。新建有砟轨道铁路CPⅢ网沿用了高速铁路无砟轨道的两种CPⅢ网形,只是精度指标有所放宽。为了降低建网费用,通过改变设站间距和观测方案,在前面两种交会网基础上,设计了两种新的CPⅢ交会网。通过计算分析,这四种方案都可以达到新规范对精度的要求。为了进一步优选既有线CPⅢ网形方案,考虑精度、可靠性及建网费用等指标,基于多目标决策方法,得到最优设计方案。最后通过敏感性分析验证了权重被修正时所选最优方案的稳定性。
1 多目标决策分析
多目标决策是基于确定的决策指标集合Z={Z1, …,Zn},在方案集合F={F1, …,Fm}中选出最优方案。不同指标的权重不同,但应满足
( 1 )
式中:wj为第j个指标的权重。
多目标决策中的主要结构为决策矩阵D,包含方案比较的定量数据
( 2 )
矩阵D中的行表示每个指标不同方案的数据,可确定该指标下的最优方案;列表示每个方案在不同指标下的数据。
方案的重要度可通过合成权重表示
( 3 )
式中:Pi为第i个方案的合成权重;pij为第i个方案在第j个指标上的权重。
多目标决策方法有AHP法[5]和TOPSIS法[6]等, 其确定权重的方法不同。最常用的是AHP法,即层次分析法,最早由Saaty提出[7],构建一个n维判断矩阵确定指标权重wj;构建n个m维判断矩阵确定权重pij。判断矩阵是根据决策矩阵中各指标的两两重要程度得到的,判断矩阵中的元素aij表示要素i与要素j相对重要度之比,aij越大,则要素i相对要素j的重要度就越高。对于一个多目标的决策问题,用n维判断矩阵A表示n个指标对目标层的重要程度,用m维判断矩阵Bi表示对于第i个特定指标m个待选方案的优劣程度。判断矩阵还需要进行一致性检验,具体方法参见文献[8],此处不再赘述。
敏感性分析的目的,是验证指标权重变化时方案重要度的稳定性[9]。修正权重可以由式( 4 )获得。对于先修正指标,有
(4a)
对于后修正指标,有
(4b)
式中:wj为先修正指标的原权重;wh为后修正指标的原权重;β为修正因子,且β≥-1;(1+β)为先修正指标的修正系数;α为后修正指标的修正系数
( 5 )
2 网形设计质量准则
网形设计质量的优劣可由精度、可靠性及费用这三类定量的指标表征。CPⅢ控制网中的方向及边长观测量可通过线性化表示为观测方程
( 6 )
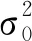
基于最小二乘原理,要求vTPv最小,可得出x的最小二乘估值为
( 7 )
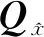
( 8 )
绝对及相对点位精度可由坐标的协方差阵计算获得,在确定观测值的先验精度后,点位精度取决于网形[10]。
多目标决策中,选择的前4个指标与精度相关,分别是:
Z1——绝对点位中误差最大值;
Z2——绝对点位中误差低于阈值(按规范[1]取3.0 mm)的比例;
Z3——相对点位中误差最大值;
Z4——相对点位中误差低于阈值(按规范[1]取1.5 mm)的比例。
控制网中存在两类不同的观测值,通常按先验定权法确定方向和距离两类观测量的权比关系[11],定权公式为
( 9 )
式中:单位权中误差σ0取为方向先验中误差σL;σS为距离先验中误差;a和b分别为光电测距固定误差和比例误差;s为测量距离。
规范要求CPⅢ网要使用方向标称精度不低于1″、测距标称精度不低于1 mm+2 mm/km×s的全站仪,测两测回[1]。则在分析网形质量时,采用的先验指标为:σ0=σL=±0.71″,a=0.71 mm,b=1.41 mm/km。
控制网的可靠性是指控制网检测粗差和抵抗残存粗差的能力,取决于多余观测数,反映在观测值的多余观测分量上[12]。可靠性矩阵R为
R=I-B(BTPB)-1BTP
(10)
式中:I为单位矩阵。
由此可见,可靠性矩阵R同样取决于系数矩阵B和权阵P,与实际观测值无关。在先验定权的情况下,矩阵R取决于控制网网形结构。
可靠性矩阵R的迹为
(11)
式中:n为观测值数目;t为参数的个数;rii为第i个观测值对应的可靠性分量。
(12)
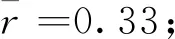
每个观测值的可靠性分量rii在0~1之间。在极端情况下,如rii=0,则该观测值的粗差无论多大,都不能被发现。所以好的网形要使可靠性分量大于某一阈值的比例尽可能大,本文将可靠性分量的阈值取为0.2。
因此,多目标决策中关于可靠性的指标有两个:
Z5——整体可靠性;
Z6——可靠性分量高于阈值的比例。
建网费用可分为交通费、人员费用、时间成本等等,难以精确量化。但是,一般而言,总的权重越小,建网费用就越低。总的权重越小,意味着观测数越少,相应时间、人员及交通费用都会减少。因此,可以用观测值权之和来表征建网费用指标[15]。
(13)
式中:pii为对应第i个观测值的权重。
多目标决策中关于费用的指标为:
Z7——观测权总和。
3 CPⅢ控制网网形布设方案
设计的既有线CPⅢ控制网的四种网形方案如下:
(1)间隔1对横向点的观测网形方案F1:这种网形在高速铁路CPⅢ控制网中采用,网形见图1(a)。相邻测站间有一对横向固定桩控制点,测站间距为60 m,控制点纵向间距为60 m,横向间距为10 m。每个测站观测4对控制点,相邻两个测站重复观测 3对控制点,每个控制点被观测4次,最长观测距离90 m。
(2)间隔2对横向点的观测网形方案F2:这种网形也在高速铁路CPⅢ控制网中采用,网形见图1(b)。相邻测站间有两对横向固定桩控制点,测站间距为120 m,控制点纵向间距为60 m,横向间距为10 m。每个测站观测6对控制点,相邻两个测站重复观测 4对控制点,每个控制点被观测3次,最长观测距离为150 m。
(3)间隔3对横向点的观测网形方案F3:网形见图1(c)。相邻测站间有三对横向固定桩控制点,测站间距180 m,控制点纵向间距为60 m,横向间距10 m。每个测站观测7对控制点,里程减小方向观测3对控制点,里程增大方向观测4对控制点,相邻两个测站重复观测4对控制点,每个控制点被两个或三个连续测站观测,最长观测距离为210 m。
(4)间隔2对斜向点的观测网形方案F4:网形见图1(d),相邻测站间有2对斜向固定桩控制点,测站间距240 m,控制点纵向间距为120 m,横向间距为10 m。每个测站观测5对控制点,每个控制点被两个或三个连续测站观测,最长观测距离为270 m。

图1 既有线CPⅢ控制网网形方案
4 模拟计算与分析
以2 km测段为试验段,计算得到四种网形的精度指标、可靠性指标和费用指标。
4.1 绝对点位精度
四种网形的绝对点位精度随里程变化规律见图2。从图2可知:
(1)距已知点越远,控制点的绝对点位精度越低,最弱点出现在相邻已知点中间位置;
(2)四种网形的绝对点位精度均小于3 mm;
(3)仅比较绝对点位精度指标,最优网形为间隔2对横向点的观测网形F2,其最大点位中误差为1.13 mm。

图2 四种网形的绝对点位中误差
4.2 相对点位精度
对于前三种观测网形,相邻点位主要有三种类型:横向10 m、纵向60 m和斜向61 m。而对于间隔2对斜向点的观测网形方案F4,相邻点位有纵向120 m、斜向61 m两种类型。四种类型相邻点的相对点位中误差见图3。
由图3可知:
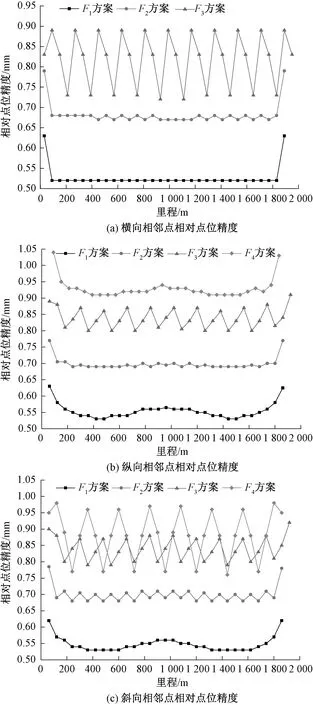
图3 四种网形的相对点位中误差
(1)测站间距越大,相邻点相对点位精度越低;
(2)四种网形的相对点位精度均小于1.5 mm;
(3)仅比较相对点位中误差指标,最优网形为间隔1对横向点的观测网形F1。
4.3 可靠性指标
网形的可靠性指标如表1所示。由表1可知:四种网形的整体可靠性均大于0.4;仅比较可靠性指标,间隔1对横向点的观测网形F1明显优于其他网形。

表1 四种网形的可靠性指标
4.4 费用指标
费用指标是既有线控制网建设时应考虑的重要指标。四种网形的工作量及观测权总和如表2所示。

表2 四种网形建网费用指标
从表2可以看到,观测权总和随着工作量的增加也相应增大,说明观测权总和可以较好地表征费用。表2说明间隔2对斜向点的观测网形F4的费用指标优于其他网形。
5 基于多目标决策的方案优选
不同指标确定的最优方案不同,因此需要基于多目标决策确定最优方案。
既有线CPⅢ网形方案优选的决策矩阵通过模拟计算得到,结果如表3所示。
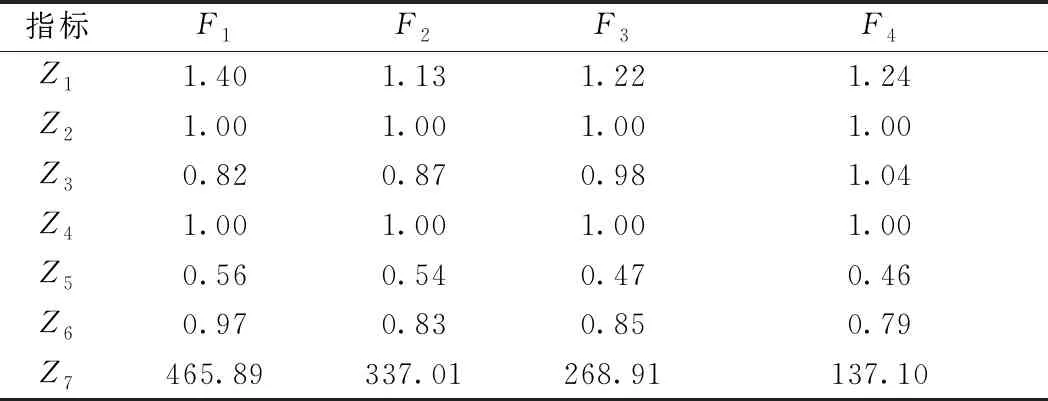
表3 CPⅢ网形方案优选决策矩阵
通过判断矩阵来确定指标权重。建立7维的判断矩阵,计算7个指标的权重,结果如表4第1行所示。指标Z2和Z4具有最大权重0.332。基于决策矩阵,建立4维判断矩阵,计算4个方案在每项指标上的权重。例如对于Z7指标,基于表3最后一行的数据,建立判断矩阵确定四个方案在该指标上的权重,结果如表4的Z7列。
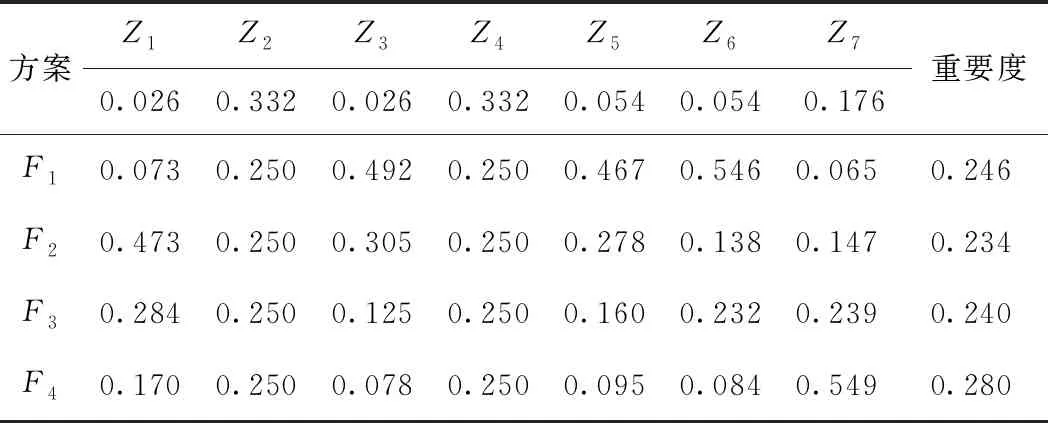
表4 四个方案重要度计算
由式( 3 )可计算出四个方案的重要度,列于表4最后一列,确定综合最优方案次序为F4、F1、F3、F2。
选取不同的修正系数和先修正指标,按式( 4 )和式( 5 )可计算28组权重方案(表5)。对于每一组权重方案,按照同样的方法计算网形方案排序,列于表6。结果表明,只有5种权重方案的排序结果与原结果不一致,且除权重方案7d外(费用权重仅为8.9%),所有权重方案下得到的最优方案均为间隔2对斜向点的观测网形方案F4。敏感性分析验证了方案F4作为综合最优既有线轨道控制网的稳定性。
6 结论
本文针对既有线轨道精调和养护要求,分析比较了四种轨道控制网网形方案,从精度、可靠性和费用三方面提出了七项评价控制网质量的指标,通过2 km测段的模拟算例,定量计算出了四种控制网的七项指标,得到以下结论:
(1)距已知点越远,控制点的绝对点位精度越低;测站间距越大,相邻点相对点位精度越低;四种网形方案在精度上均可满足绝对点位精度在3 mm内,相邻点的相对点位精度在1.5 mm内的规范要求。
(2)仅就单项指标而言,会得到不同的最优网形;通过多目标决策分析,确定了综合最优的间隔2对斜向点的观测网形方案F4,该方案建网费用最低。
(3)通过敏感性分析验算了28组权重方案,验证了观测网形方案F4作为综合最优方案的稳定性,其适合在既有线轨道控制建网中推广使用。

表5 修正权重
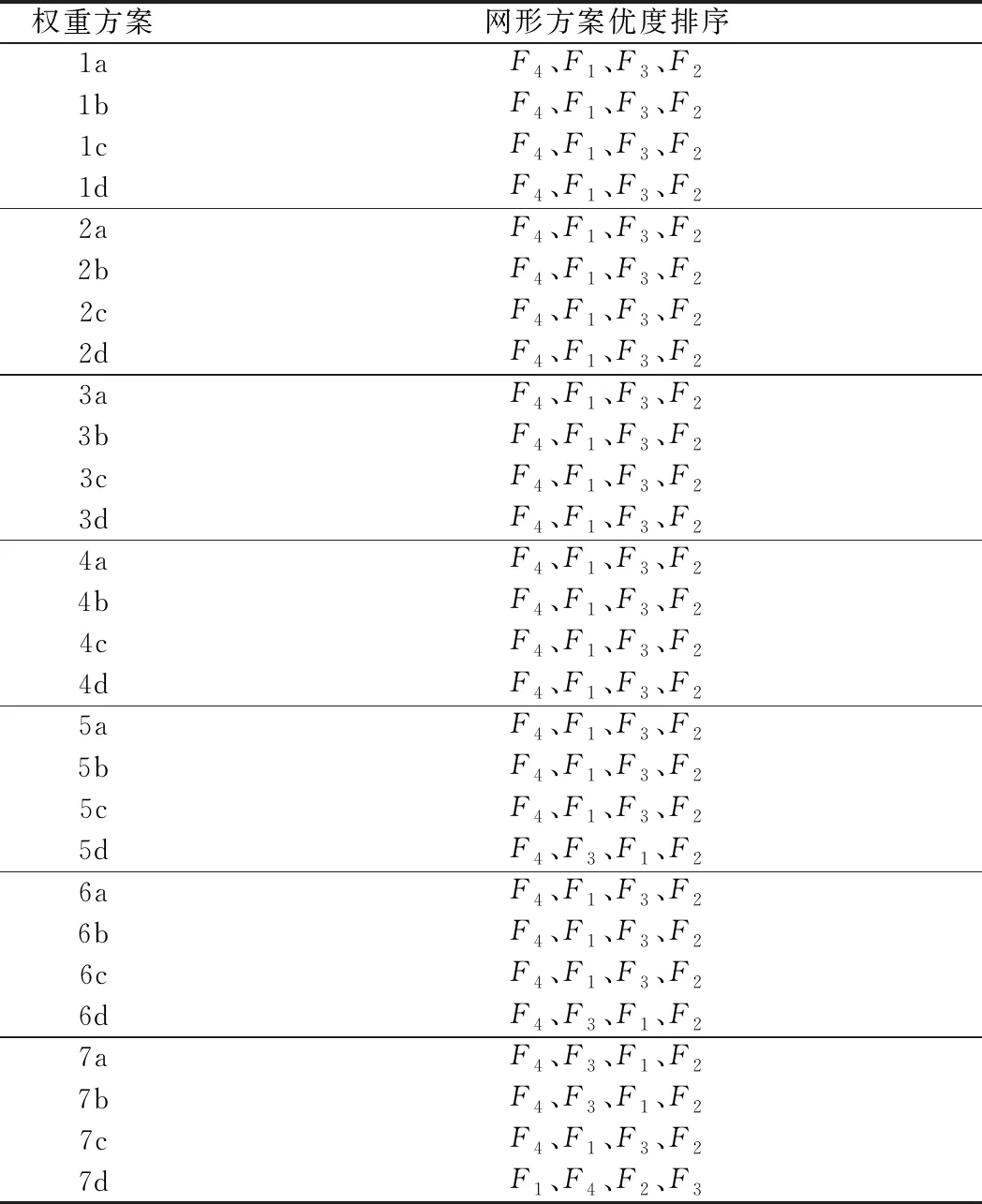
表6 不同权重方案下的网形方案排序

