输入受约束的高速列车鲁棒自适应动态面控制
徐传芳,陈希有,丁丽娜,3,王 英,李卫东
(1.大连理工大学 电气工程学院,辽宁 大连 116024;2.大连交通大学 电气信息学院,辽宁 大连 116028; 3.大连海洋大学 信息工程学院, 辽宁 大连 116023)
在给定期望速度和位移曲线的前提下,能否实现对目标曲线的高品质追踪,直接影响列车运行的安全与节能[1]。但是由于高速列车的运行过程是一个环境复杂多变、工况变化频繁的复杂非线性动力学系统[2],使得实现高速列车速度和位移的高精度跟踪极具挑战性。建立符合实际的高速列车动力学模型,考虑高速列车运行的实际情况,设计合适的跟踪控制算法,适时调整施加到列车车轮的牵引转矩与制动转矩,实现高精度的速度和位移跟踪控制具有重要的意义。
针对高速列车的速度-位移跟踪控制问题,诸多学者进行了一系列颇有成效的研究。文献[3]提出了高速列车的多模型广义预测控制方法,设计了高速列车的控制力。文献[4]基于力观测器,对施加到列车车轮的牵引转矩和制动转矩进行了设计,方法简单可行。文献[5]提出了高速动车组集成模型的自适应速度跟踪控制算法,对列车的牵引力和制动力进行了设计。文献[6]基于浸入与不变理论,设计了高速列车的间接自适应控制器,可以实现列车的跟踪误差以指数形式收敛到一个与模型参数变化率有关的有界残集中。文献[4-6]均实现了高速列车对目标曲线的精确跟踪。然而上述文献在设计控制算法时均未考虑输入约束问题。输入约束可能会导致系统性能下降甚至系统不稳定[7-8]。高速列车运行时,牵引转矩与制动转矩受到黏着防滑[9]以及执行器饱和[10]等方面的限制,在设计控制器时同样需要考虑输入约束问题。为此,文献[11]考虑饱和约束以及多级牵引/制动带来的输入非线性,提出了自适应控制策略,实现了精确的速度与位移跟踪。文献[12]考虑执行器饱和非线性,针对高速列车的自动驾驶系统(ATO系统),提出了一种新的鲁棒自适应控制方案,在确保闭环系统稳定的同时,取得了理想的跟踪性能,速度跟踪误差和位移跟踪误差均可收敛到一个较小的紧集内。
虽然文献[11-12]考虑了输入约束问题,但是文献[11-12]和文献[4-6]一样, 在建立高速列车动力学模型及设计控制算法时,均未考虑牵引转矩与制动转矩的产生过程,均将牵引转矩与制动转矩(或牵引力与制动力)作为系统的控制输入。如果考虑牵引转矩与制动转矩产生的动态过程,将牵引电机的期望转矩作为系统的控制输入,这样的模型更符合实际情况[13]。文献[14]考虑牵引/制动动态以及不确定的非线性阻力,在自适应控制中融合反步控制,实现了高速列车速度与位移的精确跟踪,但是未考虑输入约束。将牵引电机的期望转矩作为系统的控制输入,并考虑其约束问题,更符合实际情况。文献[14]还存在需要求取虚拟控制量的微分,计算量大的问题,这一问题同样存在于采用自适应反步控制实现高速列车速度与位移跟踪控制的文献[15]中。
针对目前在期望速度和位移跟踪控制中存在的问题,本文考虑输入约束,基于考虑牵引转矩与制动转矩产生动态过程的高速列车动力学模型,提出一种新的高速列车鲁棒自适应动态面控制算法,并进行了严格证明。采用在高速列车牵引/制动控制中运用尚不多见的动态面控制[16],使用跟踪微分器代替一阶滤波器[17],避免了常规反步控制中需要对虚拟量多次求取微分的困难,而且由于跟踪微分器为一种快速而精确的信号滤波器,可以获得良好的闭环性能;采用只需较少对象信息的扩张状态观测器[18],在线估计由系统未知函数和未测量状态等构成的系统总的不确定性;借鉴文献[19]中的方法,构造附加系统处理输入饱和约束问题;利用实际控制信号和虚拟控制信号中的鲁棒项补偿由扩张状态观测器和跟踪微分器产生的滤波误差。仿真结果表明,所提算法可以实现高速列车对期望速度和位移的精确跟踪控制。
1 高速列车动力学模型
1.1 考虑转矩动态过程的高速列车动力学模型
假设每个驱动轮对所传递的牵引力(或制动力)相同,根据牛顿力学原理,高速列车车体的动态特性可以描述为
( 1 )
式中:M为列车的质量;v为列车的速度;Fr为列车的运行阻力;nt为驱动轮对个数;Ft为列车运行过程中,一个驱动轮对所产生的列车牵引力(牵引时)或制动力(制动时),其大小受到诸如轮轨间黏着防滑、执行器输出饱和等因素的限制,在不发生空转/滑行的情况下,Ft的大小等于轮轨之间的黏着力Fa。
轮轨黏着力Fa是与列车轮轨接触面实时状况有关的复杂函数,其表达式为
Fa=μ(λ)Mg
( 2 )
式中:g为重力加速度;μ(λ)表示黏着系数,是蠕滑率λ的非线性函数,国内外应用较为广泛的是Burckhardt模型,其表达式为
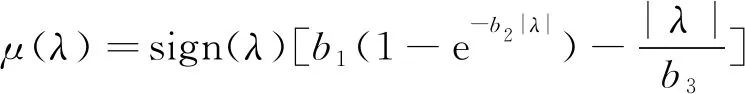
( 3 )
其中,b1,b2,b3为正数,不同的参数表示不同的轮轨黏着条件。λ为蠕滑率(λ∈[-1,1]),表示轮轨之间微量滑行的程度,其定义为[20]
( 4 )
式中:ω为车轮角速度;r为车轮半径。
高速列车的运行阻力Fr包括列车运行过程中所受到的空气阻力和轨道阻力。
Fr=M[a0+a1v+a2v2+o(·)]
( 5 )
式中:a0,a1,a2为正实数,其数值由具体的运行环境决定;o(·)表示由轨道引起的随机不稳定干扰阻力。假设o(·)有界,其引入的扰动项不会对列车运行造成不可控的影响。
列车车轮的动态方程为
( 6 )
式中:J为车轮的等效转动惯量;B为车轮的黏滞摩擦系数;Tm为作用到列车车轮的牵引转矩或制动转矩。忽略转矩传递过程中的损耗,则有
Tm=TnRg
( 7 )
其中:Tn为牵引电机的输出转矩;Rg为齿轮箱传动比。
上述建立的高速列车动力学模型描述了从作用到列车车轮的牵引转矩/制动转矩到列车运行状态之间的动态关系。然而司机驾驶列车或ATO(列车自动驾驶)控制列车时,并不是直接输出和调节牵引/制动转矩(或牵引/制动力),而是通过调整牵引/制动手柄级位或由ATO发出控制指令,传递给列车牵引或制动系统,进而实现对列车的控制。因此,如图1所示,考虑牵引/制动转矩产生的动态过程,建立能描述从控制指令输入到列车运行状态之间动态关系的高速列车动力学模型,更符合列车的实际运行情况。

图1 考虑牵引/制动转矩产生动态的列车动力学模型
当只考虑列车再生制动情况时,施加到列车车轮上的牵引转矩与制动转矩产生机理相同,因此,牵引/制动动态过程可以用相同的方程来描述。考虑到电机的电磁时间常数远小于列车的机械时间常数,因此可忽略转矩产生的具体细节,近似用一个一阶微分方程来描述这个动态过程[13],即
( 8 )
式中:Tz为牵引电机的期望转矩,为控制变量;α为一阶惯性时间常数;β为增益,均为大于零的常数。
高速列车在运行过程中,列车车轮速度和车体速度并不相同,两者之差为蠕滑速度vs,即
vs=ωr-v
( 9 )
由式( 1 )、式( 6 )~式( 9 )以及列车位移x与速度v之间的关系, 得到考虑牵引与制动转矩产生动态过程的高速列车动力学模型方程。
(10)
式中:x为列车的实际位移;L为集总参数项
(11)
1.2 输入约束
牵引转矩与制动转矩受到黏着防滑[9]以及执行器饱和[10]等限制,因此在针对式(10)所示系统进行高速列车运行控制算法设计时,需要考虑牵引转矩与制动转矩受限引起控制输入Tz存在约束的问题。控制输入Tz的约束形式可表示为
(12)
式中:Tc为所设计的期望控制输入;Tmax和Tmin分别为控制输入约束的上、下限幅值。
2 鲁棒自适应动态面控制器设计

(13)
式中:q为任意选择的正实数。对式(13)求导得
LTn+Ftd
(14)
式中:Ftd为由未知函数、未完全测量状态以及不确定性参数等构成的系统总的不确定项。
(15)
控制器的控制目标是针对式(10)构成的系统,考虑输入饱和约束及Ftd的不确定性,设计合适的控制输入,保证高速列车的实际速度和位移能够跟踪期望速度和位移,同时闭环系统稳定,所有信号都有界。
Step1令es=s,则有
(16)
引入扩张状态观测器估计不确定项Ftd。定义观测误差η11=ζ1-es,设计扩张状态观测器的形式为
(17)
其中,ζ1,ζ2为观测器状态,其中ζ2用来在线估计系统总的未知不确定项Ftd;ρ11,ρ12为扩张状态观测器的反馈增益。fal(·)函数的具体表达式为
(18)
式中:π,δ为设计参数;η为观测器误差。
定义式(17)所示观测器的估计误差为ε11=ζ2-Ftd,根据参考文献[21-22],存在有限时间T,当t>T时,η11,ε11满足|η11|≤ι11,|ε11|≤ι12,其中,ι11,ι12均为大于零的常数。
选择Tn作为式(16)所示子系统的虚拟控制,定义Tn与虚拟控制量Tnd之间的误差为eT,即
eT=Tn-Tnd
(19)
设计虚拟控制量Tnd为
(20)
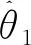
(21)
其中,γ1和σ1均为正的常数。
构造Lyapunov函数为
(22)
式中:
对式(22)求导可得
(23)
根据Young不等式[23],如下关系式成立
(24)
(25)
根据反正切函数性质,有
(26)
由式(23)~式(26)可得
(27)
Step2对式(19)求导可得
(28)
(29)
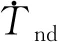
考虑式(12)所示的输入约束条件,当控制器的输出和被控对象的实际输入出现不一致的情况时,为避免控制系统失稳,构造附加系统对控制指令进行补偿[19],即
(30)
式中:σT为附加系统的状态;kσT>0,为待设计参数;ψT为一很小的正数,其值可根据系统跟踪性能要求适当选取;ΔT=Tz-Tc,Tz为实际控制输入,Tc为所设计的控制输入。
设计如下形式的控制输入
(31)
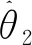
(32)
其中,γ2和σ2均为正的常数。
(33)
(34)
式中:kξT>0,为待设计参数;φT>0,为根据跟踪性能要求而选取的恰当值。
选取Lyapunov函数
(35)
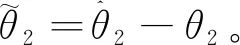
(36)
由Young不等式有
(37)
又由于eTΔT-|eTΔT|≤0,再结合反正切函数性质,可得
(38)
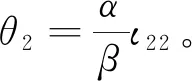

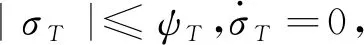
3 稳定性分析
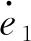
证明:选取如下的Lyapunov函数
V=V1+V2
(39)
对式(39)求导,并结合式(27)和式(38)有
(40)
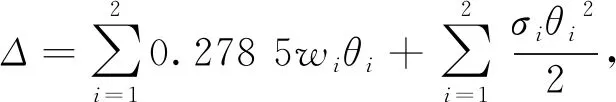
(41)
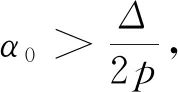
(42)
进一步可得到
(43)
可知,V(t)最终有界,系统的所有信号均半全局一致最终有界。同时因为
(44)
因此,当t→∞时,es的收敛域满足如下紧集
(45)
即
(46)
由此可得到
(47)
式中:e0为e1的初始值。由式(47)可知,e1的收敛域满足如下紧集
(48)
进一步可得到
(49)
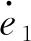
(50)
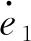
以上证明过程针对的是|σT|≥ψT时的情况,即存在输入饱和约束时的情况。当|σT|<ψT时,不存在输入饱和,此时ΔT=0,即Tz=Tc。
若在控制器设计时不考虑输入约束,则控制器为
(51)
需要注意的一点是,从控制算法的推导过程来看,增大α0可以减小列车的速度跟踪误差和位移跟踪误差,但是α0也不能太大,否则系统的控制增益增大,会导致高增益的控制策略,从而激发系统的未建模动态,降低系统的暂态性能。因此在设计控制器参数的时候要在确保系统稳态跟踪误差的基础上合理选择。
4 仿真结果与分析
为了验证本文所提出建模与控制方法的有效性,利用一个具有两节动力车厢的列车模型进行仿真验证。列车模型主要采用CRH2型高速列车的基本参数,具体参数为:驱动轮对数nt=8,每节车厢的平均质量为55 t,平均轴重N=134.75 kN,车轮的转动惯量J=80 kg·m2,车轮半径r=0.43 m,齿轮箱传动比Rg=85/28。取黏滞摩擦系数B=0.1。由于轨道阻力会受到落叶、轨道不平等因素的影响,而这些因素引起的干扰具有随机性,因此本文在仿真中引入一时变的正弦函数0.009 4sin(0.02t)来表示由轨道引起的随机不稳定干扰阻力,从而列车的运行阻力表示为
Fr=110(0.052+0.003 8v+0.000 112v2+
0.009 4sin(0.02t)
(52)
扩张状态观测器和跟踪微分滤波器的参数设置为ρ11=5,ρ12=20,π11=0.5,δ11=0.025 ;ρ21=30,ρ22=40,π21=0.4,δ21=0.027 ;黏着系数以及自适应律和附加系统的参数见表1、表2。

表1 黏着系数的具体参数

表2 控制器、自适应律及附加系统的参数
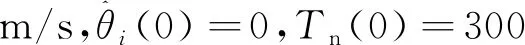
为了验证所设计的控制方法在高速列车处于不同运行工况下的跟踪性能,仿真模拟高速列车在1 000 s内的运行过程,运行距离为47.5 km,整个过程包含两个加速阶段、四个巡航阶段、一个减速阶段和一个制动阶段。分别对考虑输入约束和不考虑输入约束两种情况进行仿真,两种情况下的仿真参数完全一致。仿真过程同时考虑了轨面状态发生突变的情况,具体轨面状态变化发生在150 s(由干燥轨面到潮湿轨面)和250 s(由潮湿轨面到干燥轨面)。
仿真结果如图2~图5所示。图2(a)和图2(b)为列车的速度和位移跟踪轨迹曲线,图3(a)和图3(b)为列车的速度跟踪误差和位移跟踪误差轨迹曲线。可以看出,高速列车工况发生变化以及遭遇轨面状态突变时,考虑输入约束和不考虑输入约束两种情况下的速度跟踪误差和位移跟踪误差均较小,它们的最大绝对值分别为0.035 m/s、0.006 7 m和0.03 m/s、0.005 7 m,两种情况均实现了对目标速度和位移的精确跟踪。图4为牵引电机的实际控制输入转矩轨迹曲线,可以看出考虑输入约束时,牵引电机的实际控制输入转矩除了暂态阶段出现输入饱和,一直在约束范围内。结合图3和图4可以看出,在饱和阶段,考虑输入约束时,系统的跟踪性能受到一定影响,但影响有限且时间短暂,当控制输入退出饱和后,速度和位移跟踪性能又恢复到了饱和前的跟踪效果。如果不考虑输入饱和,当遭遇黏着系数较小的路况时,不受限制的控制输入有可能使得高速列车的牵引力(或制动力)大于轮轨间的最大黏着力,可能导致车轮发生空转(或滑行),系统趋于不稳定。图5为基于扩张状态观测器的系统总的不确定量Ftd的估计,可以看出所设计的扩张状态观测器实现了对被观测量Ftd的精确观测,它使得控制器可以很好的补偿系统中的未知不确定项,从而保证了精确的速度和位移跟踪性能。
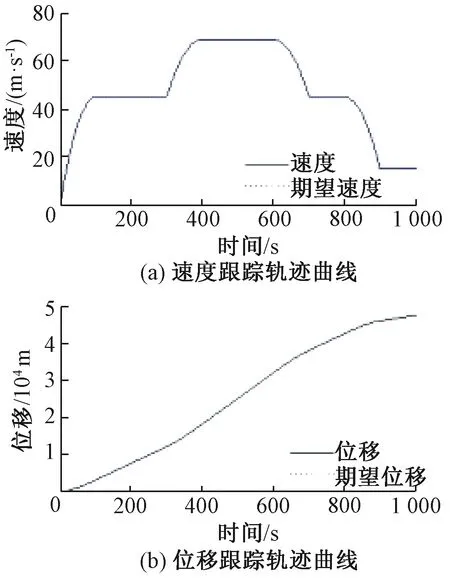
图2 速度和位移跟踪轨迹曲线

图3 速度和位移跟踪误差轨迹曲线
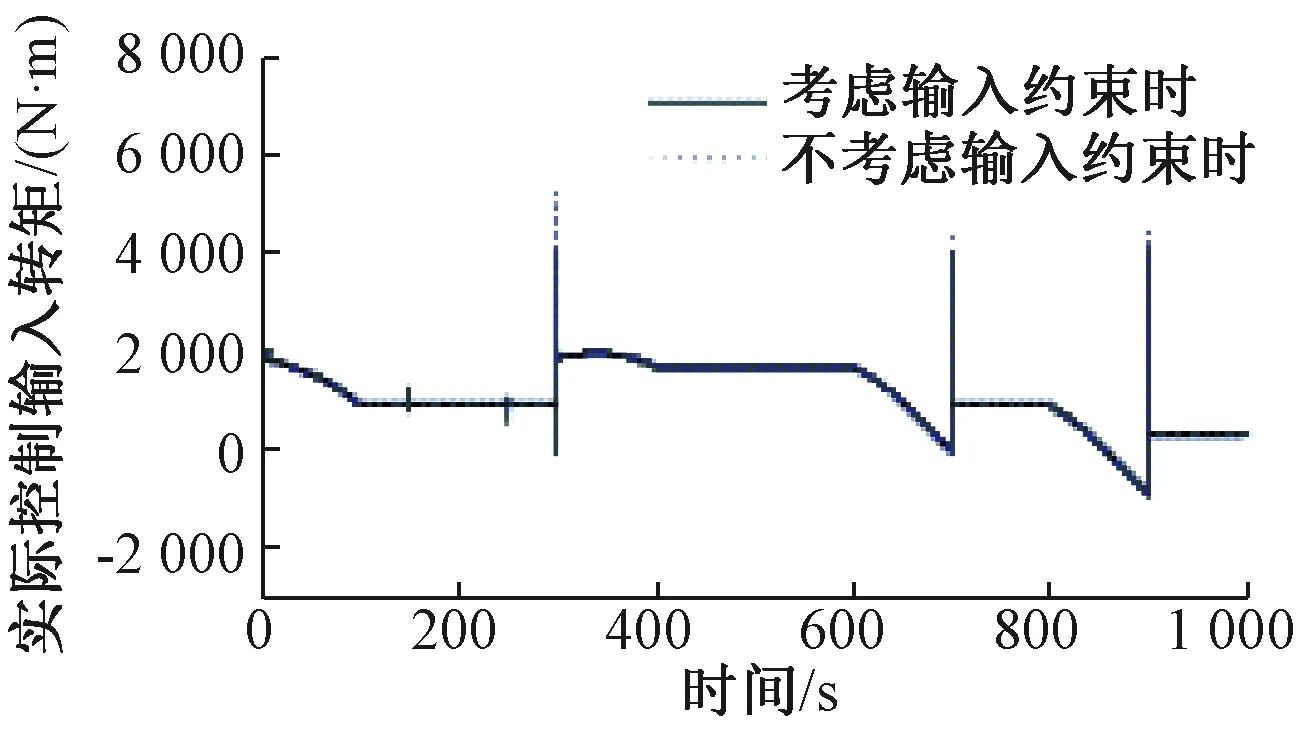
图4 牵引电机的实际控制输入转矩轨迹曲线
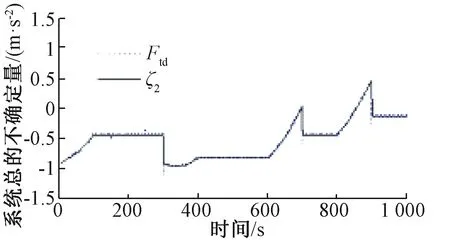
图5 基于扩张状态观测器的Ftd估计
5 结束语
本文考虑牵引/制动动态,建立高速列车的运行模型,该模型描述了从牵引/制动系统控制输入到列车运行状态之间的关系,能更好地反映列车的动力学特性。基于所建立的模型,考虑输入饱和约束,提出高速列车的鲁棒自适应动态面控制算法。仿真结果表明,本文算法可精确估计系统总的不确定项,有效处理输入饱和约束,并可补偿扩张状态观测器和跟踪微分器产生的滤波误差,实现高速列车对期望速度和位移的精确跟踪,为高速列车的跟踪运行控制研究提供了参考。轮轨黏着防滑引起的约束实际是一动态输入约束,如果在控制策略中融入实时黏着防滑约束,则可构建一套高速列车主动安全跟踪控制系统,能主动避免列车的空转/打滑等危险运行状态,提高列车的行车安全,这是作者下一步拟研究的内容。

