基于季节分解和SARIMA-GARCH模型的铁路月度客运量预测方法
钱名军,李引珍,阿茹娜
(1.兰州交通大学 交通运输学院,甘肃 兰州 730070; 2.中国中铁股份有限公司 规划发展部, 北京 100039)
铁路客运系统作为一个与外界频繁进行能量、信息交换的典型的开放、动态、非线性复杂巨系统,其客运量时间序列是该系统运转所产生的外在表现数据。它蕴含了旅客运输过程中的大量信息,是各种因素对铁路客流综合作用的结果,呈现出复杂的变化趋势和波动特性。因此,有必要深入研究铁路客运量时间序列,从中提取并利用有关规律信息,为铁路客运部门灵活制定列车开行计划、合理配置和运用客车车底,提高客运服务质量乃至科学制定路网规划建设方案等提供决策参考。
当前,对客运量时间序列的预测研究,主要运用神经网络[1-2]、机器学习[3-5]、混沌理论[6]、ARIMA(Auto-Regressive Integrated Moving Average)模型[7-8]、灰色理论[9]、马尔科夫模型[9-10]或卡尔曼滤波等技术方法来提高对数据的拟合精度。文献[1]提出了消除高铁节假日影响的数据替补修正法和融合变分模态分解(VMD)、遗传算法(GA)及BP神经网络的VMD-GA-BP客运量预测法。文献[3]提出一种基于深度学习与神经网络相结合的小时客流预测模型SAE-DNN,并将其应用于厦门市BRT公交站的客流预测。文献[6]将相空间重构方法用于对与铁路运量相关的时间序列进行混沌特性识别,并采用最大Lyapunov指数预测方法对铁路客货运量进行预测分析。文献[7]针对移动假日对铁路客运量的双峰影响,采用X-12-ARIMA季节调整模型,建立铁路客运量的三时段春节季节调整模型,取得了较好效果。文献[8]针对北京地铁进站客流呈现以“周”为周期的波动规律,采用了SARIMA季节时间序列模型进行预测。文献[10]将指数平滑法与马尔科夫模型综合用于公路客运量预测。可见,现有客运量预测研究或侧重于对宏观的年度增减趋势进行预测,或侧重于对相对微观的节假日、周、日客运量进行预测,而对中观层面的月度或季度客运量变化规律及特点的研究不够深入。
伴随经济和社会的快速发展,人们的出行需求更加多元化、动态化,为及时响应旅客需求的快速变化以适应客运市场的激烈竞争,铁路客运组织计划在保持运能与运需基本均衡的前提下需具备一定的灵活性。而目前铁路部门在制定旅客运输计划时大多参照年度客流数据进行决策,对月度或季度客流所反映出来的短期波动变化响应不够及时。年度客流数据虽然能较好地反映铁路客运市场中长期的变化趋势,但时间跨度仍然较大,在一定程度上掩盖了一年中不同月份客运量的季节性、周期性和随机波动性,不利于客运组织部门及时灵活地调整旅客列车开行计划、机车车辆运用计划等以适应月度客运市场的相应变化。
实际上,铁路月度或季度客运量在受铁路自身运能影响的同时,还与近期国民经济发展状态、季节气候以及其他交通方式的相互作用有关,具有明显的中长期变化趋势性和周期性;同时又因移动节假日效应或突发重大事件的存在,而具有显著的随机波动性。因此,对月度客运量变化规律进行研究具有重要的现实意义。文献[11]针对铁路月度客运量序列中存在的趋势成分和季节成分构建出SARIMA(2,1,1)(0,1,0)12模型,其预测精度较Excel趋势线法、XGBOOST算法略有提高,但预测效果仍不算理想。主要原因在于,该SARIMA模型定阶不够准确,且关键是对序列中存在的非线性波动成分(即ARCH异方差效应)未予以考虑并进行有效提取。
基于此,本文以铁路月度客运量时间序列为研究对象,首先,对其趋势性、季节性和随机性进行季节分解,并通过季节、非季节差分序列的相关图识别筛选出拟合优度更高的SARIMA基础模型。然后,为消除异方差、提高模型预测精度,再对SARIMA基础模型的回归残差进行GARCH效应建模,得到SARIMA(2,1,1)(1,1,1)12-GARCH(1,1)融合模型。最后,对融合模型的稳定性及预测性能进行检验、分析。
1 SARIMA-GARCH融合预测方法
研究表明,铁路月度客运量时间序列具有非平稳、非线性、周期性以及存在异方差性,为此将SARIMA模型与GARCH模型进行融合建模[12-13],以提高预测精度。
1.1 季节时间序列模型SARIMA
SARIMA从自回归差分移动平均模型ARIMA衍生而来[7]。该模型通过对非平稳时间序列进行差分转化为平稳时间序列后,将因变量仅对它的滞后项及随机误差项的现值和滞后值进行回归来构建模型,很适合非平稳单变量时间序列的预测。
若某时间序列经s个时间间隔后观测值呈现出相似性,如同时出现波峰或波谷状态,则称该序列是以s为周期的季节时间序列。令周期为s的非平稳季节时间序列(包括日、周、月或季度序列)为{Yt}(t为时间序列样本长度),则其经d阶非季节差分、p阶自回归、q阶移动平均的ARIMA(p,d,q)模型为
ΔdYt=c+α1ΔdYt-1+α2ΔdYt-2+…+
αpΔdYt-p+ut+β1ut-1+β2ut-2+…+βqut-q
(1)
式中:c为常数项;α1,α2,…,αp为自回归系数;β1,β2,…,βq为移动平均系数;ut为随机扰动项。
式(1)右边前半部分为自回归过程,后半部分为移动平均过程。
显然,式(1)等价于
ΔdYt-α1ΔdYt-1-α2ΔdYt-2-…-αpΔdYt-p=
c+ut+β1ut-1+β2ut-2+…+βqut-q
(2)
引入滞后算子L,可以得到
LΔdYt=ΔdYt-1
LnΔdYt=ΔdYt-n
式中:n为任意正整数。
特别地L0ΔdYt=ΔdYt。
则式(2)可写为
(1-α1L-α2L2-…-αpLp)ΔdYt=
c+(1+β1L+β2L2+…+βqLq)ut
(3)
令平稳的自回归算子
Φp(L)=1-α1L-α2L2-…-αpLp
可逆的移动平均算子
Θq(L)=1+β1L+β2L2+…+βqLq
代入式(3)即得ARIMA(p,d,q)简式
Φp(L)ΔdYt=c+Θq(L)ut
(4)
同时,定义季节差分算子Δs=1-Ls,则一次季节差分表示为
ΔsYt=(1-Ls)Yt=Yt-LsYt=Yt-Yt-s
(5)
对于非平稳季节性时间序列,需经D阶季节差分来消除季节性影响,才可建立周期为s的P阶自回归、Q阶移动平均季节时间序列模型
(6)
式中:AP(Ls)、BQ(Ls)分别为非平稳季节时间序列的自回归算子与移动平均算子。
当式(6)的随机扰动项ut非平稳且存在自回归(Auto-Regressive, AR)或移动平均(Moving Average, MA)成分时,再对ut建立ARIMA(p,d,q)模型
Φp(L)Δdut=Θq(L)vt
(7)
式中:vt为白噪声。
把式(7)代入式(6),即得SARIMA(p,d,q)×(P,D,Q)s模型
(8)
显然,当P=D=Q=0时,SARIMA(p,d,q)×(P,D,Q)s模型退化为ARIMA(p,d,q)模型,因此说ARIMA是SARIMA的特例。当p=d=q=P=D=Q=0时,SARIMA模型退化为白噪声模型。
1.2 广义自回归条件异方差模型GARCH
通常,非平稳时间序列模型的方差不仅随时间变化,而且有时变化剧烈,表现出“波动集聚(Volatility Clustering)”特征,即方差在一些时段比较小,而在另一些时段会比较大。这种现象就说明模型残差存在异方差效应(ARCH)。当存在ARCH效应时,有必要对异方差进行正确处理以使回归参数的估计量更具显著性,避免异方差对时序模型产生不良影响,从而提高模型的预测精度。GARCH模型可以用于对解释变量的方差建模,以提高均值方程参数估计的有效性。
GARCH(p,q)由ARCH(q)模型扩展而来[14]。ARCH(q)模型由诺贝尔经济学奖获得者恩格尔提出,它针对均值方程的残差波动项建立模型并用于预测,模型表达式为
均值方程:
Yt=F(t,Yt-1,Yt-2,…)+ut
(9)
式中:F(t,Yt-1,Yt-2…)为时间序列{Yt}的确定信息拟合模型,本文为所建SARIMA(p,d,q)×(P,D,Q)s模型。
条件方差方程为
(10)
式中:It-1为已知信息集;ω0为常数项。
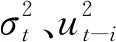

(11)
式中:ω为ARCH项参数;θ为GARCH项参数。

综上,GARCH模型考虑了异方差效应对时序模型的影响,能对因变量的方差进行更准确的预测,因此可以提高均值方程参数估计的有效性,改善时序模型的预测精度。
2 铁路月度客运量时间序列特征分析
本文从国家统计局官网提取到2005年1月—2019年5月年共173组铁路月度客运量统计数据,构成时间序列研究样本。
2.1 月度时间序列的平稳性检验
由图1可知,铁路月度客运量序列与时间呈指数关系,非线性、非平稳性和趋势性显著,且存在递增型异方差,直接建模难以取得良好效果。所以,建模前先对原始序列Y取自然对数得LY序列(异方差得到一定程度抑制,见图2),再对LY序列进行平稳化处理和单整性检验。

图1 客运量原始序列Y的时序图
本文采用ADF单位根检验法来判定时间序列的平稳性。若不平稳,则对LY序列依次进行d阶差分直至序列平稳,再进行分析建模。对LY序列的平稳性ADF检验结果见表1。

图2 客运量对数序列LY的时序图

表1 LY序列ADF检验结果
检验结果分析:(1)LY序列的ADF检验统计量均大于1%、5%和10%水平的临界值,且接受存在单位根的原假设的概率为0.348 8。所以,LY序列是非平稳序列。(2)经一阶差分后的序列ΔLY对应的ADF检验统计量为-20.246 6,小于1%的显著水平临界值,其接受存在单位根原假设的概率为0,即不接受原假设,表明ΔLY是平稳的。同时,从一阶差分序列ΔLY的时序图3也可看出,差分序列围绕0轴上下波动,呈现出良好的平稳性。综上,LY序列为一阶单整序列,记为LY~I(1)。
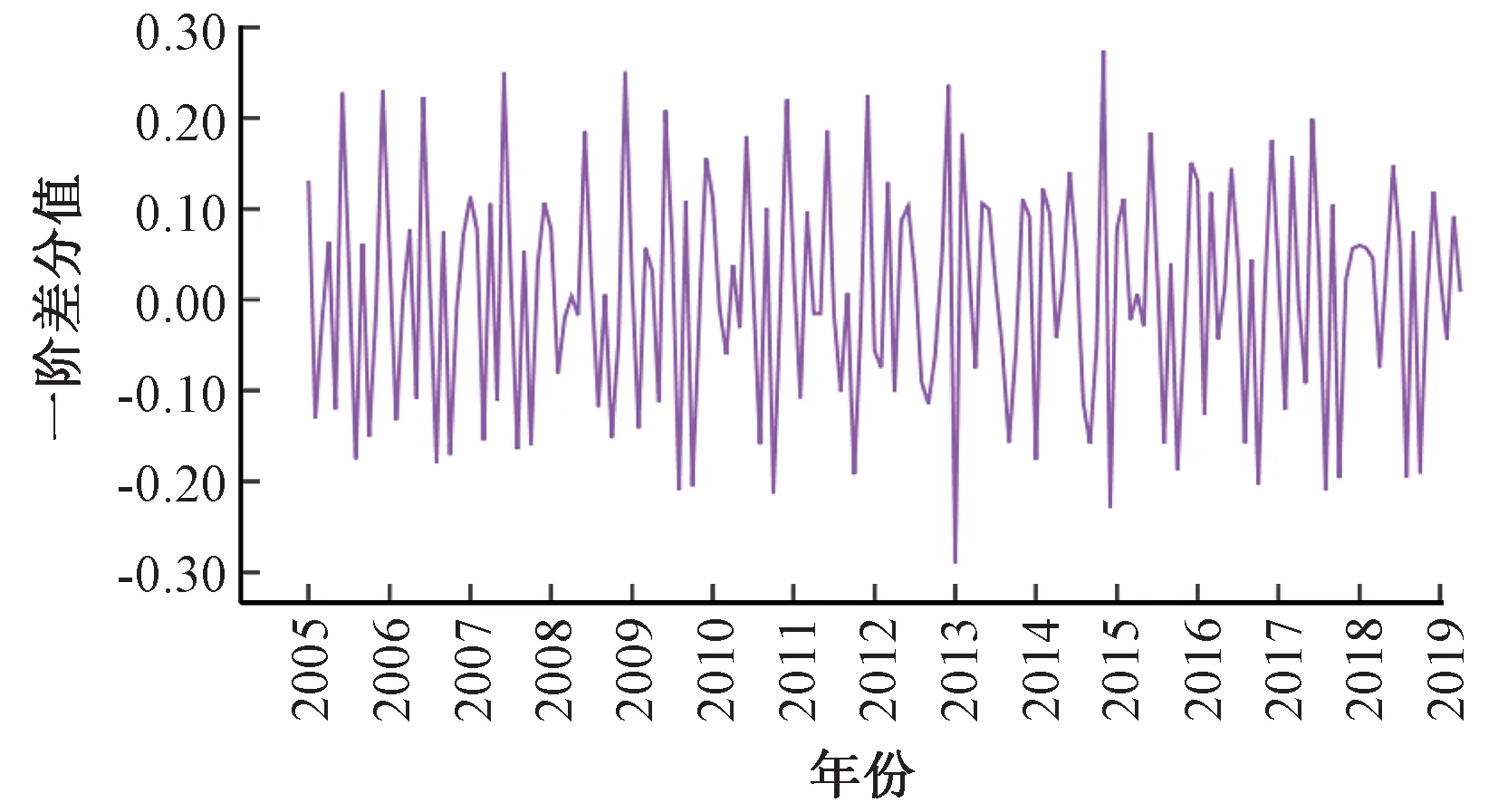
图3 一阶差分序列ΔLY的时序图
2.2 月度客运量时间序列特征信息分解
为了直观准确表征趋势因素、季节因素和随机因素的存在,本文根据铁路月度客运量序列具有递增型异方差特性,采用季节分解的乘法模型,把{Yt}分解为趋势循环分量Tt、季节分量St和随机分量It:Yt=Tt×St×It。
具体分解步骤有如下3个阶段[15]:
第一阶段:初始季节因素调整
(12)
该移动平均能保留线性趋势,消除12阶不变季节性,并减少不规则成分方差。
(13)
从原序列中剔除趋势循环分量后即得到季节-随机成分。
(14)
式中:

(15)
即对每个月的观测值分别进行3×3的季节移动平均,将初步估计的季节成分剔除其2×12项简单移动平均,以消除季节分量中的残余趋势。
(4)季节调整结果的初始估计
(16)

第二阶段:精确季节因素调整


(17)
式中:H为Henderson加权移动平均项数,随机分量I越大,需要的项数越多;h为Henderson加权移动平均系数。
(18)
(19)
式中:
(20)
(4)季节调整结果的二次估计
(21)
第三阶段:估计最终的趋势循环分量和随机分量
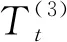
(22)
(23)
最终得到季节分解乘法模型的各分量序列
(24)
按照式(24)方法提取出月度客运量序列中的趋势循环分量、季节分量和随机分量,见图4~图6。
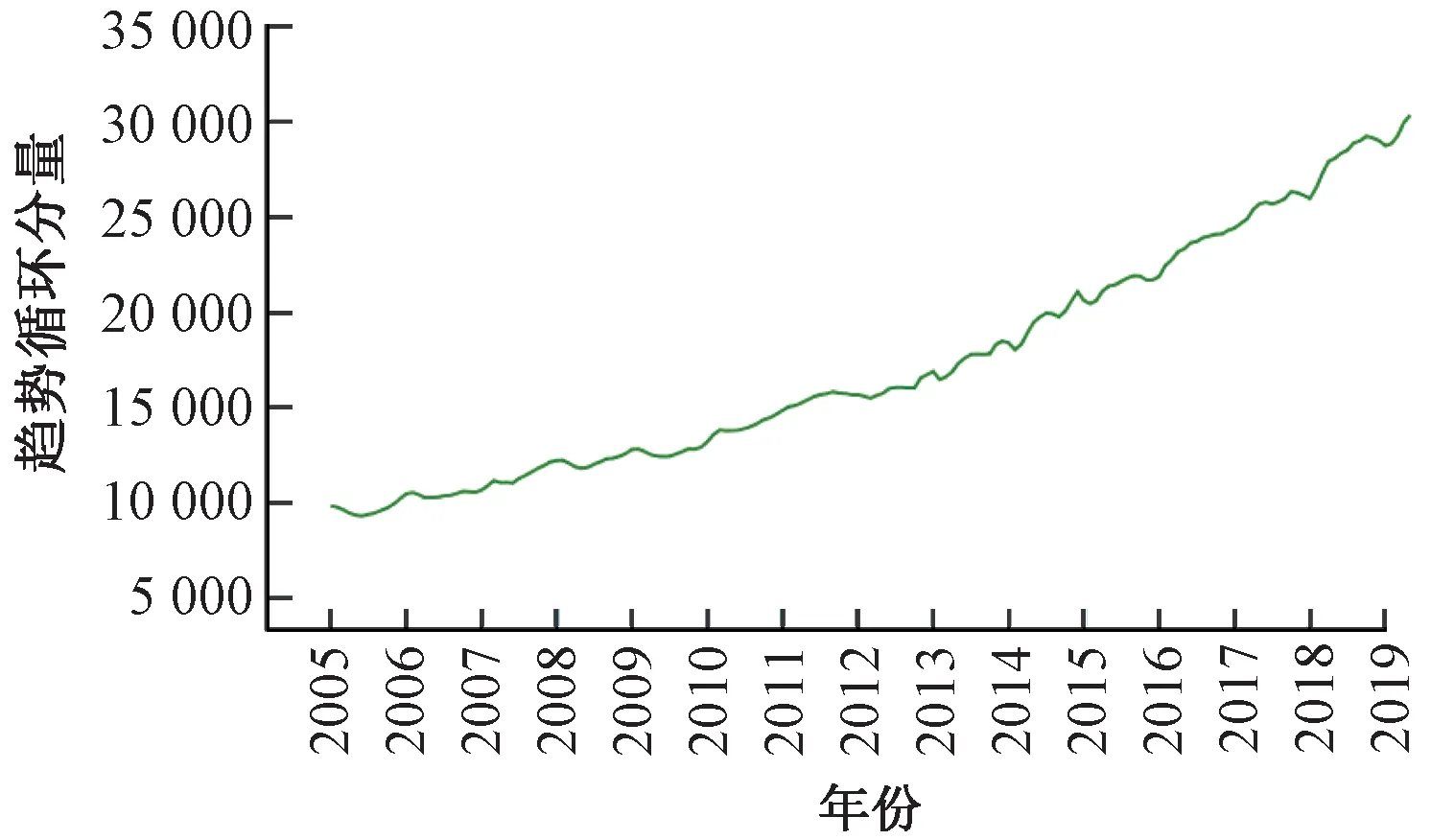
图4 铁路月度客运量趋势循环分量Tt

图5 铁路月度客运量的季节分量St
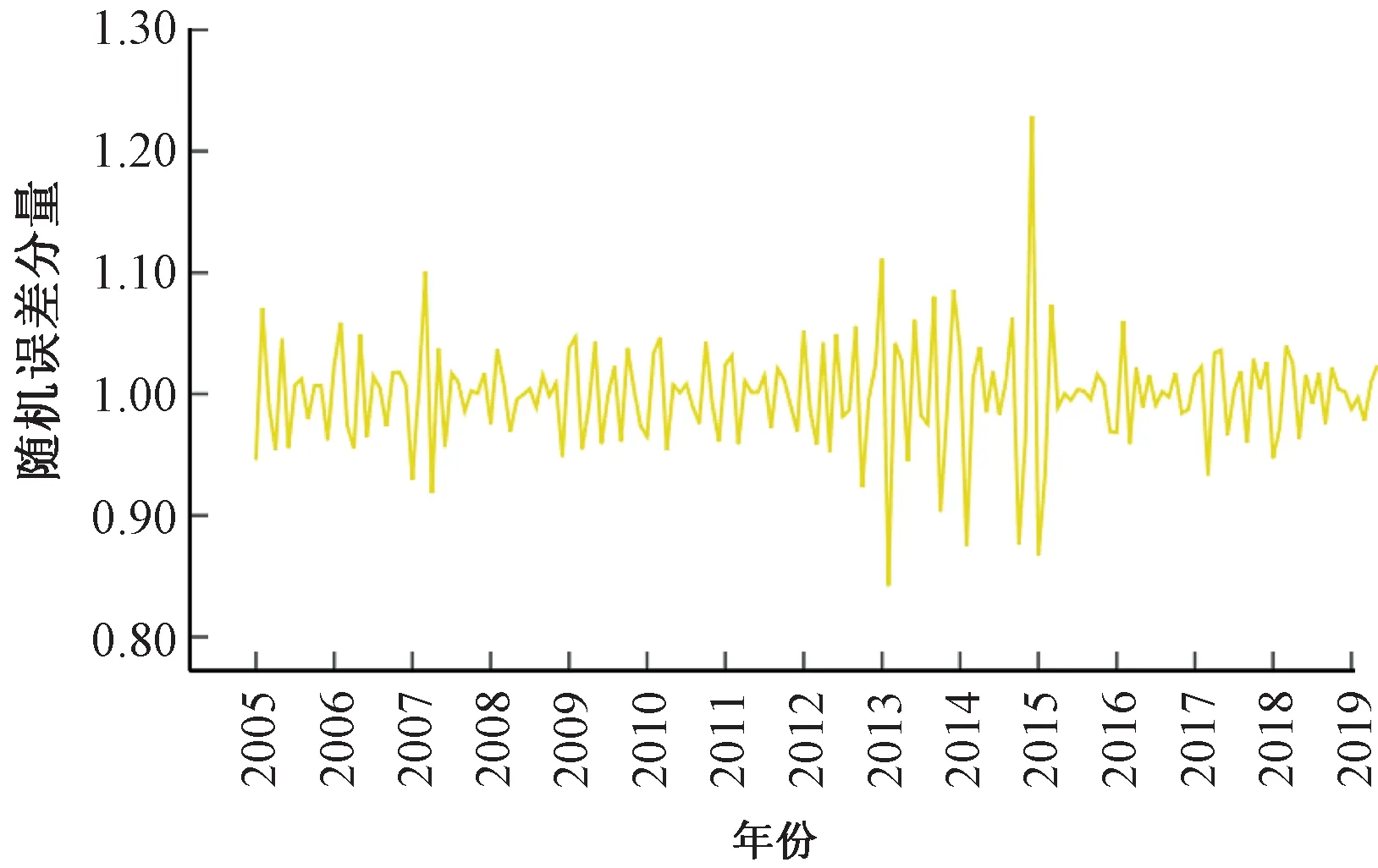
图6 铁路月度客运量的随机分量It
从月度客运量序列的成分分解时序图可见,客运量各分量随时间的变化特性差异较大,呈现明显的趋势性、季节周期性以及随机性特征。所以,铁路月度客运量时间序列适宜采用乘法季节模型进行预测。
3 月度客运量的SARIMA-GARCH预测模型构建
经上述量化检验和分析可知,对数序列LY经一阶差分后平稳。因此,可以对LY序列进行建模。
3.1 SARIMA(p,d,q)(P,D,Q)s基础模型构建
(1)确定周期s和差分次数d、D
本文以月度数据为研究样本,即周期s取12。同时,从LY的相关图7也可以看出,其自相关系数呈线性缓慢衰减,在滞后期为12的整倍数时点上出现自相关系数绝对值较大的峰值;这在ΔLY序列的相关图8中体现尤其明显,12的整倍数时点出现峰值,且呈振荡式衰减变化。

图7 对数序列LY的自相关、偏相关图

图8 一阶差分序列ΔLY的自相关、偏相关图
这足以证明序列存在显著的以12为周期的季节波动,这与实际情况一致。因此,需对其进行季节性差分(或12阶差分)。对数序列LY的一阶差分ΔLY平稳,即非季节差分次数d取1。对ΔLY进行一次季节性差分后得到ΔΔ12LY序列,其时序图见图9、相关图见图10。
由图9可知ΔΔ12LY序列围绕0轴上下小幅波动,呈现良好的平稳性。同时,图10也显示在滞后期12的整倍数时点处的相关系数在2倍标准差范围内,说明其季节性成分已被充分提取。综上,季节性差分次数D取1可满足平稳性要求。
(2)模型阶数判别
观察图10,结合表2的模型阶数判别方法,可以看到自相关和偏相关图都呈欠阻尼状态震荡衰减,非季节自相关系数呈1阶或2阶截尾,即非季节项AR的阶数p可取1或2。同时,由于平稳序列ΔΔ12LY中大部分季节性波动已被消除,其周期12整倍数时点的季节自相关系数在2倍的标准差范围缓慢衰减,自相关性明显减弱,说明针对该序列建立滞后1阶和12阶上的SARIMA 模型是合适的,即模型的非季节项MA的阶数q取1,季节项SMA的阶数Q也取1。季节项SAR的阶数P可取0(按拖尾衰减处理)或1(按1阶截尾处理)。据此,可初步确定符合要求的四个SARIMA(p,d,q)(P,D,Q)12模型:(1,1,1)(0,1,1)12、(1,1,1)(1,1,1)12、(2,1,1)(0,1,1)12和(2,1,1)(1,1,1)12。

图9 ΔΔ12LY的时序图

图10 ΔΔ12LY的自相关、偏相关图
(3)SARIMA模型拟合优度检验及筛选
对上述4个备选季节模型进行拟合优度检验,见表3。

表2 模型阶数判别表

表3 模型拟合优度检验结果
表3中的调整后可决系数R2表示模型的整体拟合优度,取值范围[0,1],该值越大表示模型拟合效果越好。赤池信息量准则AIC、施瓦茨信息量准则SC取值越小表明模型拟合精度越高。DW值表示模型残差的不相关程度,范围在0~4之间,该值越接近2表明自相关程度越低,建模效果越好。通过表3的检验结果对比,SARIMA(2,1,1)(1,1,1)12模型的可决系数R2最大,AIC和SC值最小,DW统计值最接近2,多项指标均显示其检验结果为最优,因此,最终选定SARIMA(2,1,1)(1,1,1)12模型对样本序列建立基础模型。
(4)SARIMA模型参数估计
取2005年1月—2018年12月期间的数据作为训练样本运用OLS方法估计出SARIMA(2,1,1)(1,1,1)12模型方程为
(1+0.420 2L+0.408 6L2)(1-0.323 3L12)ΔΔ12LYt=(1-0.661 0L)(1-0.797 6L12)vt
(25)
t统计量:(-4.821 3)(-4.498 6) (2.287 7) (-7.957 2) (-6.367 0)
R2为0.675 7,标准差(Standard Error,SE)为0.054 4,残差平方和(Residual Sum of Squares,RSS)为0.441 7,AIC值为-2.893 1,SC值为-2.775 3
可见,该方程各参数统计量均较显著,初步拟合效果较好。
3.2 SARIMA-GARCH融合模型构建
(1)SARIMA模型残差的ARCH效应检验
在进一步构建GARCH(1,1)模型前,需对基础模型SARIMA(2,1,1)(1,1,1)12残差进行ARCH检验。首先,观察SARIMA(2,1,1)(1,1,1)12模型残差时序图11,发现残差波动存在“集聚”现象:波动在一些时段内较小,在一些时段内又变得很大。据此初步判断残差序列存在ARCH效应。
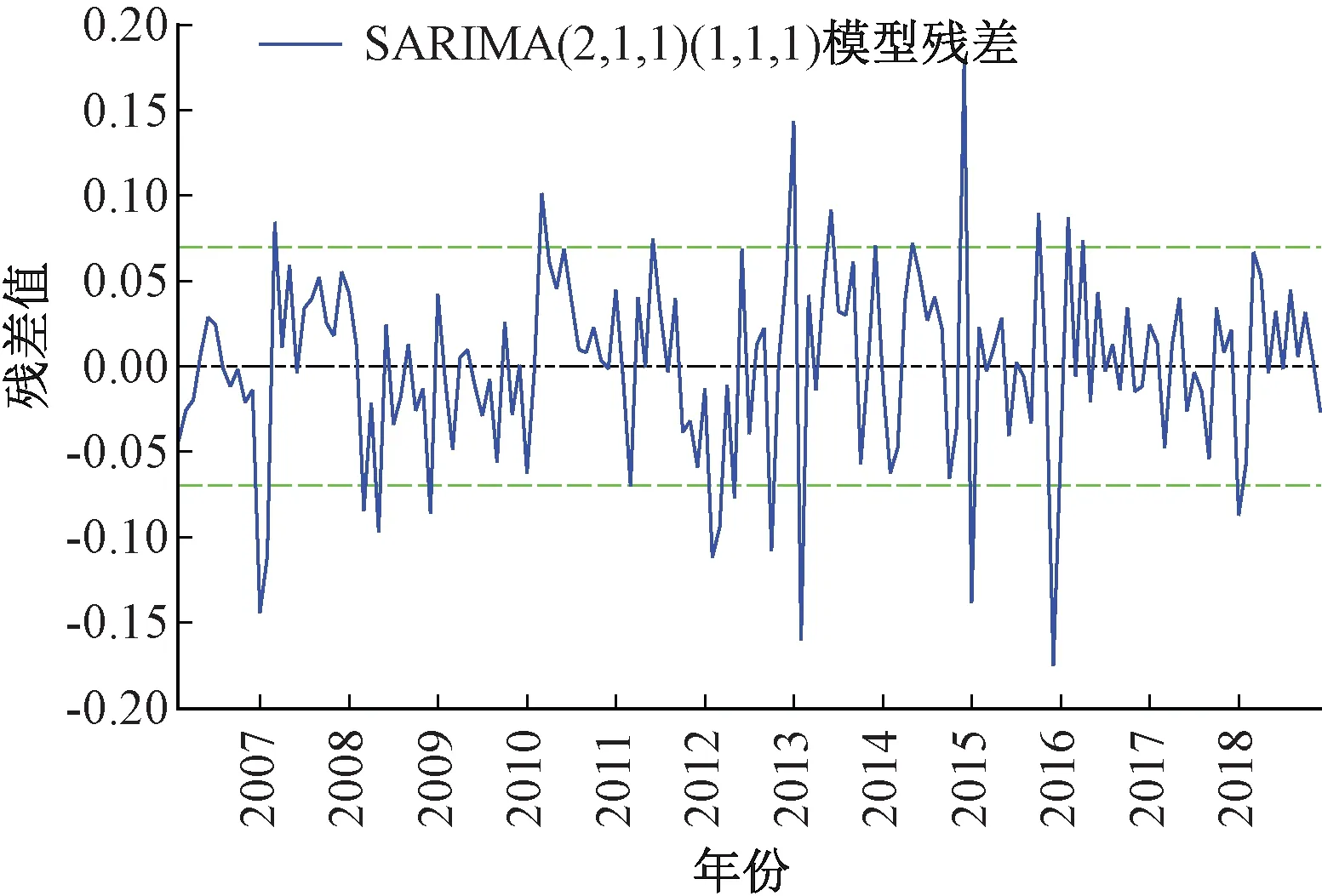
图11 SARIMA(2,1,1)(1,1,1)12模型残差时序图
为进一步证实模型残差序列具有ARCH效应,本文采用White检验法对其进行ARCH效应量化检验。检验结果见表4。

表4 SARIMA(2,1,1)(1,1,1)12模型残差ARCH检验结果
从表4中可见,F统计量、LM统计量均显著,其接受残差序列是同方差的原假设的相伴概率P值都为0,即拒绝原假设,残差序列存在显著的异方差。
(2)构建SARIMA-GARCH融合模型
在SARIMA(2,1,1)(1,1,1)12的基础上考虑ARCH效应后重新对序列进行极大似然估计,可得SARIMA(2,1,1)(1,1,1)12-GARCH(1,1)融合模型为
均值方程:(1+0.399 1L+0.407 3L2)(1-0.248 0L12)ΔΔ12LYt=(1-0.652 5L)(1-0.898 6L12)vt
(26)
t统计量: (-4.584 0) (-4.368 3) (3.443 2) (-8.487 1) (-44.309 3)

(27)
t统计量: (2.068 4) (23.840 2)
R2为0.902 3,SE为0.033 0,RSS为0.381 9,AIC值为-3.994 8,SC值为-3.879 3
与式(25)的SARIMA模型相比,考虑了条件异方差所建立的SARIMA-GARCH融合模型拟合优度R2有了较大改善,参数统计量更为显著,标准差、残差平方和以及AIC、SC值也显著缩小。均值方程各参数估计值有小幅修正,方差方程ARCH项、GARCH项系数均统计显著。ARCH、GARCH项系数都为正,满足了参数约束,系数之和近似为1,表现出良好的收敛性。这充分说明SARIMA-GARCH融合模型能更好地拟合铁路月度客运量数据。
3.3 模型稳定性检验
得到SARIMA-GARCH模型后,为避免拟合过程中还有重要信息丢失,需进一步检验模型的稳定性,即对残差的异方差效应和自相关性进行检验分析,若模型不稳定则解释力有限。
(1)模型残差的ARCH-LM检验
采用ARCH-LM方法检验方程残差的条件异方差,结果见表5。

表5 SARIMA-GARCH模型残差ARCH检验结果
检验得到F统计量、LM统计量均不显著,相伴概率P值均为0.55,即接受同方差的原假设,说明引入GARCH模型后消除了原残差序列的异方差效应。
(2)模型残差的平方相关图检验
通过残差平方相关图和Q-统计量对模型残差进行检验,见图12。
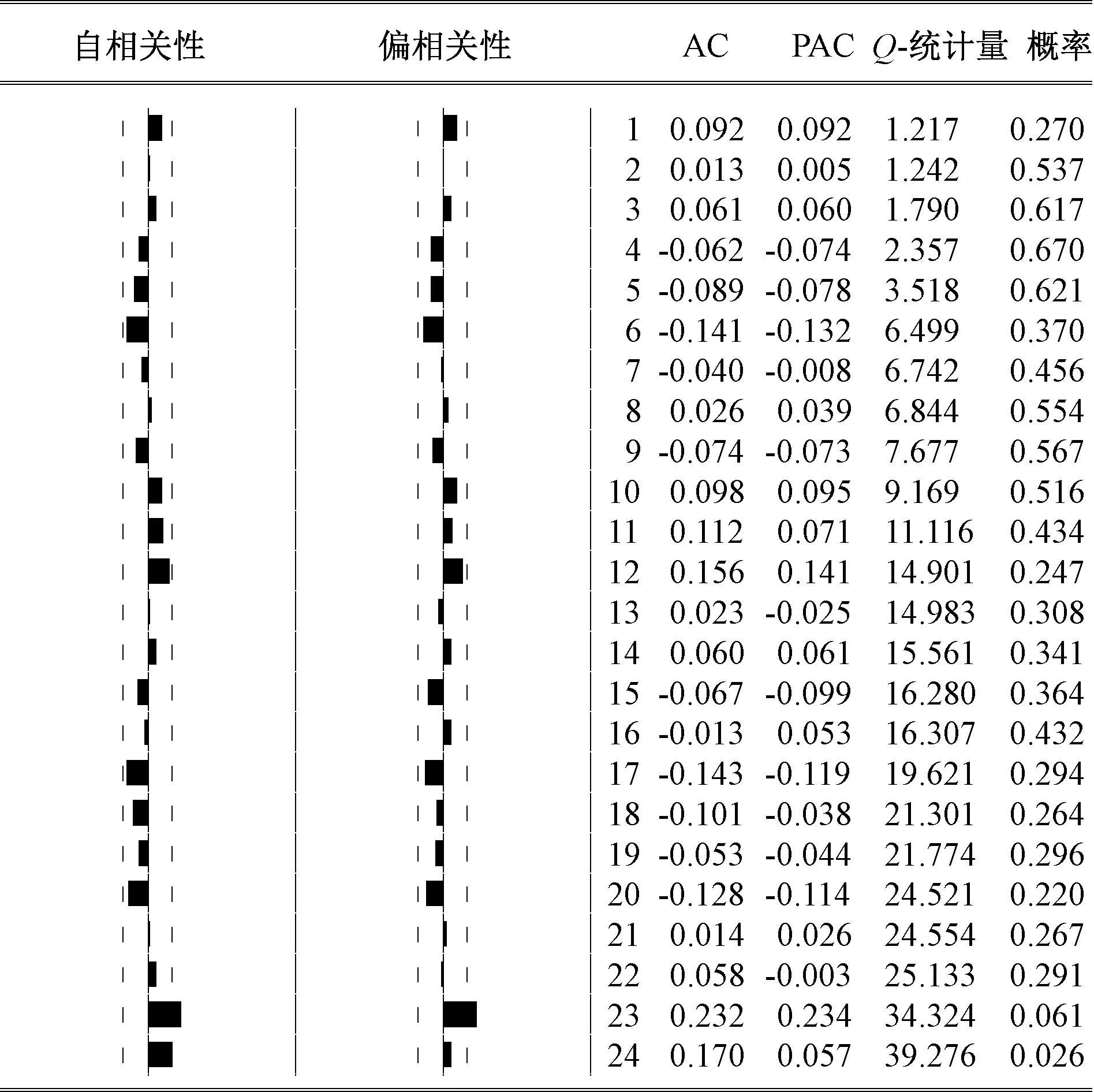
图12 SARIMA-GARCH模型残差平方相关图
由图12可知,模型残差的ACF和PACF值均显著地落在2倍的标准差范围内,自相关和偏自相关系数近似为0,残差序列为同方差的原假设的相伴概率值均大于10%,可以认定残差序列为白噪声,即模型已将原时间序列的信息基本提取完毕。
综上,所建SARIMA-GARCH稳定性良好,对建模数据的解释力较强。
4 模型预测精度验证对比及性能评价
为验证所建模型的有效性,将SARIMA-GARCH模型与常规SARIMA、ARIMA和NAR动态神经网络等时序模型的短期预测值进行精度对比,并对该模型的中长期预测效果进行分析。
4.1 模型短期预测精度对比
以2019年1—5月份的客运量数据作为测试样本,将SARIMA(2,1,1)(1,1,1)12-GARCH(1,1)模型与SARIMA(2,1,1)(1,1,1)12、ARIMA(2,1,1)和NAR动态神经网络模型的短期预测值进行精度对比见表6。
对比表6中4种模型的短期测算结果,可以看到所构建的SARIMA-GARCH融合模型与SARIMA基础模型的稳定性更好,平均绝对百分误差均小于5%,而ARIMA模型和NAR动态神经网络模型的稳定性要差些,平均绝对百分误差也大于5%。这表明,前两类模型在对具有季节性变化的时间序列建模时更具优势,其建模效果较好。同时,由于SARIMA-GARCH融合模型考虑了时间序列中存在的异方差效应,提高了对波动性的刻画精度,使得预测值与实际值接近程度更高、偏差更小,短期预测精度比单纯的SARIMA模型更好。因此,所建模型的数据拟合能力较强,短期测算精度较高。
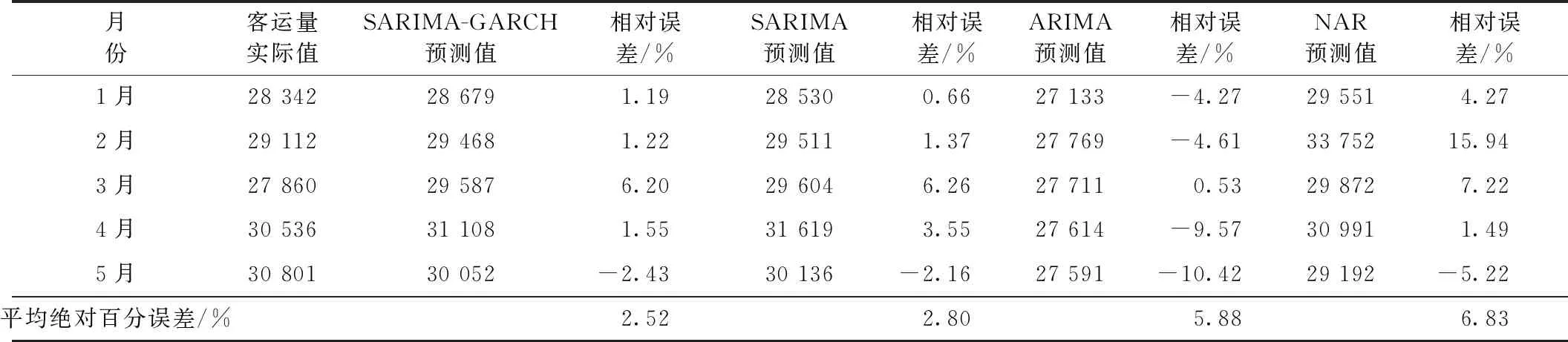
表6 2019年1—5月铁路月度客运量预测误差比较
4.2 模型中长期预测性能评价
本文选取平均相对误差δMPE、Theil不等系数U、偏差比σBP、方差比σVP和协方差比σCP等多个评价指标对模型中长期预测性能进行验证评价。
(1)平均相对误差δMPE
(28)
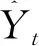
(2)Theil不等系数U
(29)
(3)偏差比σBP
(30)
(4)方差比σVP
(31)
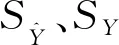
(5)协方差比σCP
(32)

以2005年1月为基期,利用所建SARIMA-GARCH模型对铁路月度客运量进行中长期测算,测算值与相应月份客运量实际值的对比效果见图13。

图13 SARIMA-GARCH模型中长期预测值与实际值对比图
从图13可见,建模期内(2019年虚线轴左侧区域)模型的中长期预测值与真实值的拟合程度也比较好。各项预测性能指标:平均相对误差MPE为5.69%,高于短期测试区(2019年1月至2019年5月条形区域)的相对误差MPE值2.52%;Theil不等系数U为0.043 7,它是不受量纲影响的相对指标,度量的是相对均方误差;偏倚比σBP为0.114 2,它表示的是系统误差,度量了预测值与实际值序列均值的偏离程度;方差比σVP为0.008 2,该值较小近乎为0,度量了预测值方差与实际值方差的偏离程度;协方差比σCP为0.877 6,略低于0.9,它衡量了剩余的非系统预测误差及模型的预测稳定性。若预测效果良好,则偏倚比σBP和方差比σVP都会比较小,而协方差比σCP会比较大,且三者之和为1。
比较而言,SARIMA-GARCH模型的中长期预测精度较短期预测有所降低,表明该模型更适合作短期预测。
5 结论
本文通过季节分解法量化分解出铁路月度客运量时间序列中的趋势循环分量、季节分量和不规则波动分量。然后,对时间序列平稳化、单整性处理后引入SARIMA模型对其季节性、趋势性进行基础建模。为进一步提高对波动性的刻画精度,消除异方差性,对基础模型残差构建了GARCH模型,得到SARIMA-GARCH融合模型。最后,为验证该模型的稳定性和实用性,将其与常规的SARIMA、ARIMA和NAR动态神经网络模型短期预测值进行精度对比分析,同时对其中长期预测效果作了测试分析。研究结果表明:
(1)铁路月度客运量具有显著的趋势性、季节性和波动性特征。铁路客运组织部门需在总体满足旅客出行需求逐渐增长的前提下,灵活地根据各月份客运量的季节性波动合理制定列车开行计划和车底运用方案。
(2)铁路月度客运量时间序列是非平稳、非线性及存在异方差效应的。在对其进行建模预测时,为确保预测精度,不能忽视其单整性和异方差性的影响。
(3)综合考虑了月度客运量序列的趋势性、季节性和波动性的SARIMA-GARCH模型能很好地拟合数据,短期预测性能良好。
基于SARIMA-GARCH的月度客运量预测模型丰富了铁路运输组织的优化理论体系,可为铁路客运组织部门制定设备运用方案或日常运营计划提供科学的决策参考。

