基于体积特征的织物瑕疵检测方法
◆李锋 李文青
(东华大学计算机科学与技术学院上海 201620)
1 引言
纺织业作为我国支柱性产业,具有极其重要的经济位置,并且具有很强的国际优势[1]。织物在纺织的过程中,高效的瑕疵检测对织物的质量和生产效率具有极大的影响。目前大部分国家和企业仍使用人工验布的方法,具有漏检率和误检率高、劳动成本高和生产效率低等问题,计算机智能瑕疵检测逐渐成为国内外学者研究新热点。机织物由相互垂直排列的纱线按一定的规律交织而成的织物,所以形成的织物在纹理上具有一定的特征,而瑕疵的出现破坏了这种规律,可以通过分析瑕疵区域与正常区域的特征,寻找到瑕疵图像与无瑕疵图像的特征差异,进而能够在织物图像中识别出瑕疵区域[2-3]。总结现有的特征提取的方法可以分为3 类[4]:基于统计的[5-6]、基于模型的[7-8]和基于频谱分析的[9-11]方法。基于统计的方法通过对图像的像素灰度值进行计算,获取能够表征图像的统计量,然后根据阈值的大小对图像进行检测。例如灰度差分法、灰度共生矩阵等方法。基于模型的方法是通过对图像的纹理结构进行建模,根据图像中模型参数的差异进行瑕疵检测,如马尔科夫随机场通过图像之间的马尔科夫模型的距离来判断图像有无瑕疵[12]。王刚[13]等人提出的基于奇异值分解的瑕疵检测算法通过奇异矩阵对图像进行重构,根据重构误差进行瑕疵判断。基于模型的方法对图像的整体纹理结构要求比较高,故应用性比较低。基于频谱分析的方法主要是傅里叶变换、Gabor 变换和小波变换等方法。该类方法适应性较差,例如傅里叶变换对局部区域瑕疵的识别能力比较差,而且对噪声较为敏感。Gabor 变换中各滤波器非正交关系,存在大量的冗余数据,不能较好地描述图像的局部结构信息。
瑕疵检测算法的重点是通过计算织物标准模板图像与待检测图像的特征差异,来判断待检测图像是否存在瑕疵。这里的特征可以是图像的灰度特征,也可以是图像的纹理特征。针对待检区域的特征值与模板的特征值差值比较大,且面积比较大的瑕疵,很多瑕疵算法检测效果表现良好。但有些瑕疵例如小洞、油污、接头、异物植入等瑕疵,这些瑕疵点与模板的特征值差异大,但是瑕疵的面积比较小;还有些瑕疵其特征值差异小,但是瑕疵具有一定的连续性和密集型,例如缺经、缺纬、双经纬、断纬等瑕疵,瑕疵区域的特征差与正常区域的特征差相差较小,但是瑕疵区域面积比较大。针对以上这些情况,如果不考虑瑕疵的形态和分布,仅仅是基于图像特征差异进行处理,是很容易将瑕疵区域误识别为图像采集过程中的噪声干扰。为此本文提出了一种基于体积特征的织物瑕疵检测方法,将待检测区域的特征差值之和作为其体积特征,相对于面积比较小,特征差异较大,或者瑕疵特征差较小但是面积比较大的待检测区域,通过体积特征进行检测,能够较好地识别出瑕疵区域。
2 算法架构
机织物是由经纬纱通过特定的编织规律织造形成,所形成的织物是具有独特的纹理特征和灰度特征,而瑕疵的出现破坏了织物的特征,造成了与标准模板图像的特征差异,然而不同的瑕疵造成的特征差异是不同的。如图1~4 所示的模板图像、瑕疵图像以及两者之间的特征差异三维图像,从图1 和图2 的破洞,油污瑕疵特征差异图,我们可以看出,瑕疵面积比较小,但是瑕疵比较明显,瑕疵区域特征差远远高于正常纹理区域的特征差;从图3 和图4 的缺纬,缺经瑕疵特征差异图,可以看出瑕疵区域特征差与正常纹理区域的特征差相差不大,但是瑕疵区域的面积比较大。因此,本文结合了瑕疵区域的面积以及特征差异两个方面来提取待检测区域的特征以实现瑕疵检测。
本文提出的基于体积特征的瑕疵检测算法的流程图如图5 所示。在对织物图像与模板图像进行特征提取,获得特征差图像,再经过二值化和形态学处理后,输出的二值图像中的区域可能是瑕疵区域也可能是干扰区域。根据前面分析我们可知,与瑕疵区域相比较,干扰区域的噪声明显程度没有油污和破洞这些瑕疵强,如果仅仅依靠干扰区域与瑕疵区域像素灰度的差异来区分瑕疵区域是不行的,因为有时候像缺经和缺纬这样的瑕疵,其瑕疵区域的像素灰度会和干扰区域的像素灰度相差不大,但是缺经和缺纬这类的瑕疵区域面积比较大,而噪点产生的干扰区域面积比较小,故本文提出的基于体积特征的瑕疵检测算法,结合了特征差异以及区域面积大小两个因素,通过待检测区域的特征差之和的大小来识别瑕疵和噪声干扰,进而达到瑕疵检测的目的。
3 基于体积特征的瑕疵检测
3.1 待检测区域

公式(1)为特征差计算公式,式(1)中F(x,y)和G(x,y)分别为标准图像与待检测图像的灰度值,g(x,y)为差值图像。再根据如公式(2)对特征差图像g(x,y)进行二值化操作,式中T为阈值。为了去除图像中的噪点,对图像进行了形态学处理,得到图像经过二值化,形态学处理得到的二值图像中,包含的待检测区域可能是瑕疵区域,也可能是噪点干扰区域,为了进一步提取区域的体积特征,需要获得区域的灰度像素集合。每一个区域内的像素具有连通性,通过连通区域提取算法可以获得待检测区域的特征差像素集合,常见的连通区域提取算法有种子填充和扫描线填充算法等[14],本文使用种子填充算法[15],像素邻域采用的是8-邻域,这样能够尽可能标识出瑕疵区域的像素集合。

图1 破洞瑕疵特征差异图

图2 油污瑕疵特征差三维图

图3 缺纬瑕疵特征差三维图

图4 缺经瑕疵特征差三维图

图5 算法框图
3.2 体积特征计算
待检测图像经过算法处理转换为二值图像,通过连通区域提取算法标记待检测区域,获得区域的像素集合。图像g′(x,y)与特征差图像g(x,y)在像素位置上是一一对应的,根据待检测区域的像素集合在特征差图像中可以得到特征差像素集合。假设图像g′(x,y)经过连通区域提取算法共标记出n个连通的待检测区域,其中第i个待检测区域用ci表示。通过公式(3)将待检测区域内mi像素的特征差值累加求和,结果即为该待检测区域的体积特征值。

3.3 阈值分割
通过公式(4),逐一将待检测区域ci的体积特征值vi与阈值V进行比较。如果待检测区域的体积特征vi大于阈值V,说明该待检测区域与正常纹理区域相比特征异常,判断ci为瑕疵区域,将待检测区域内的像素值标记为前景像素值;如果待检测区域的体积特征小于或者等于阈值V,说明该待检测区域特征比较正常,则ci为噪声,将区域内的像素值标记为背景像素值,算法最后通过输出的二值图像是否有疵点来判定待检测图像是否为瑕疵图像。
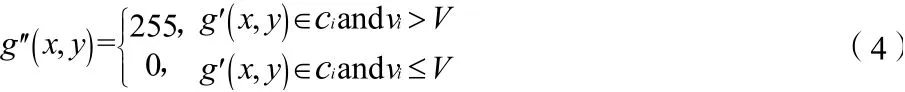
式中255 为二值图像的前景像素值,0 为二值图像的背景像素值。
4 体积阈值参数学习
在上述算法中,阈值V的大小对瑕疵检测的效果具有较大的影响,如果V过大,将会漏检真正的瑕疵区域,如果阈值过小,又不能很好地将干扰去除,所以准确计算阈值V是至关重要的。
正常情况下,对无瑕疵图像,灰度特征应当是具有区域规律性,而实际上图像在采集的过程中会引入噪声,造成图像的局部灰度特征发生变化。为了使得阈值V具有一定的适应性,进而提高算法的科学性,本文将根据无瑕疵图像噪点干扰区域的灰度特征计算阈值V,具体步骤如下。
(1)首先动态随机采集多幅无瑕疵图像作为训练图像,将标准模板图像与每幅训练图像分别进行灰度特征匹配,获得特征差图像,然后根据本文算法流程最终获得训练图像的体积特征。
(2)此时训练图像的体积特征表示为噪声干扰区域的特征,为了能够更好地区分瑕疵和噪声,本文提取每幅图像体积特征的最大值,然后计算其平均值作为本文瑕疵算法中的体积阈值。
5 实验及分析
5.1 实验平台
为了验证本文算法的有效性,选取了含有破洞、油污、缺经、缺纬、接头5 种瑕疵类型,每种瑕疵类型50 幅图像,图像分辨率为256*256。在对算法检测效果进行评估中,瑕疵区域标记为1,无瑕疵区域标记为0,对专家标记瑕疵图像和算法输出图像进行对比。专家标记瑕疵图像与算法输出图像均为1 的部分为真阳性(TP),均为0 的部分为真阴性(TN),算法输出图像标记为1,瑕疵图像专家标记为0 的部分为假阳性(FP),反之为假阴性(FN)。本文实验中使用的评价指标有准确率(ACC)、真阳性率(TP)、伪阳性率(FPR)、阳性预测值(PPV)、阴性预测值(NPV),各项指标定义如下:

5.2 实验分析
如图6 表示出织物图像集中5 种瑕疵类型的待测瑕疵图像、灰度特征差图像、特征差图的二值化图、形态学处理结果图以及本文算法检测结果图。从图6(b)的特征差图像可以看出,瑕疵点区域与正常纹理区域的灰度对比度得到明显增强,说明灰度特征能够很好地区分瑕疵区域与正常纹理区域。由图6(c)~(d)示,经过二值化以及形态学操作,对待检测区域进行膨胀填充,增强了图像中待检测区域的纹理结构,同时去掉了几何面积比较小的待检测区域。计算待检测区域的体积特征,根据体积特征进行瑕疵识别的结果图如图6(e)所示,从算法输出的图像中可以看出,通过体积特征对待检测区域进行阈值分割,较好的区分出瑕疵区域和噪声,同时能够很好地保留瑕疵区域的位置和形状。

图6 本文算法瑕疵检测流程结果图
织物图像集的实验测试结果量化结果如表1 所示,在评价指标中,对于TPR,PPV 和NPV 数值越大越好,FPR 数值越小越好。从表1中的统计结果可以看出,本文算法的ACC 均在94.5% 之上,TPR平均值在97% 左右,FPR 平均值为3.8%,PPV 平均值72.3%,NPV均在98.9% 以上。由图6 的本文算法检测流程结果图和表1 的统计数据可知,本文算法对织物图像测试集中的瑕疵检测效果较好。
5.3 实验对比
为了进一步检验本文提出的瑕疵算法的检测效果,这里将本文提出的算法与基于直方图特征的瑕疵检测算法进行了对比。两种算法对不同瑕疵的检测效果,如图7 所示。图7(a)为瑕疵样本图像,图7(b)是本文提出的算法对瑕疵图像的检测结果,图7(c)是直方图特征算法对瑕疵图像的检测结果。由图7 可知,两种算法都检测到了瑕疵,同时将瑕疵从图像背景中分割了出来,但是从整体的瑕疵检测效果来看,基于直方图特征的瑕疵检测算法对瑕疵造成了削弱,不能完整的检测出瑕疵的形状和位置,而本文提出的算法能够较好地消除背景纹理和噪声的影响,特别是针对具有密集型和连续性且特征不是很明显的瑕疵,能更加准确的检测出瑕疵的位置和形状。
在对比实验中,对100 幅样本图像集进行瑕疵检测,包含40 幅无瑕疵样本图像,60 幅不同瑕疵样本图像,其中瑕疵样本图像中包含20 幅瑕疵特征比较明显,但是面积比较小(以下用“特征a”表示)的样本图像,20 幅瑕疵特征不明显,但具有一定的密集型和连续性(以下用“特征b”表示)的样本图像,另外20 幅图像瑕疵特征明显,且面积比较大。然后使用本文提出的算法和直方图特征算法分别对样本图像集进行瑕疵检测,检测统计结果如表3 所示。表2 中将图像瑕疵类型分为点状瑕疵、条状瑕疵和网状瑕疵,同时统计了两种算法对“特征a”和“特征b”瑕疵样本图像的检测效果,结果如表3 所示。从表2 中可以看出,本文算法的TPR 以及FPR 高于直方图特征算法,主要是因为本文算法采用的阈值V 较大,经过腐蚀、膨胀操作,待检测区域的面积增大,造成其周围的无瑕疵区域被检测成瑕疵区域。从表3 可以看出,本文提出的算法对“特征a”和“特征b”瑕疵具有很好的检测效果,直方图特征算法对“特征a”和“特征b”瑕疵具有一定的检测率,但是其算法只能检测出瑕疵的部分纹理,大大削弱了瑕疵的形状和瑕疵的定位。整体对比实验表明,本文提出的算法可以很好地消除噪声的干扰,对整体瑕疵的检测效果更为准确。

图7 本文算法与直方图算法瑕疵检测效果图

表1 本文算法对5 种瑕疵图像检测结果统计

表2 本文算法与直方图算法瑕疵检测效果统计

网状99.35 99.23 1.38 76.81 99.26 本文算法96.67 78.52 0.52 78.67 94.96 直方图算法

表3 本文算法与直方图算法对“特征a”与“特征b”瑕疵检测效果统计
6 结论
本文提出的基于体积特征的织物瑕疵检测方法,通过计算待检测区域的灰度特征差之和,作为区域的体积特征用于瑕疵判定,既考虑了灰度特征差异,又考虑了瑕疵分布特征,能够充分识别瑕疵。实验结果表明,本文算法能够更好地去除环境干扰,同时提取不同尺寸形状的瑕疵,准确率高达96.5% 以上;特别是针对“特征a”以及“特征b”类型瑕疵,本文算法能够完整地检测到瑕疵大小以及位置。在之后的瑕疵算法研究过程中,还需对织物图像的纹理类型、瑕疵种类等方面进行深入探讨,以测试本文算法在各种不同类型织物下的适应性。

