两端子III-V 族多结太阳电池串联的光伏特性
王宏
(大同煤炭职业技术学院,山西 大同 037003)
1 引言
美国国家可再生能源实验室(NREL) 在十几年前的研究中就已经开始构想并研究GaInP/GaAs 叠层太阳电池[1],其结构如图1 所示。在这种电池中,上部的GaxIn1-xP(带隙宽度为1.8~1.9 eV)子电池生长在晶格匹配的GaAs 底电池上,两子电池间通过隧道结实现互相连接,如图2 所示。当x≈0.5 时GaxIn1-xP 带隙宽度为1.8~1.9eV,且与GaAs 的晶格常数相同。从理论上讲,叠层电池其效率可以|达到36%~40%[2]。其结构包括在硅衬底上机械叠层几个宽禁带的顶电池和单片式叠层AlGaAs、GaAs 和GaInAs,或者在硅上叠层GaAsP。但是这种机械叠层结构成本高而且笨重(可能是技术尚未成熟)。在单片结构中(例如GaAs 和GaInAs,或者GaAsP 和Si),底电池和顶电池晶格不匹配产生的缺陷是一个不容易解决的问题。因此在原材料和生长系统中AlGaAs 对痕量级氧的敏感性使得产量很难提高,这也就限制了其规模化量产。

图1 GaInP/GaAs 多结太阳电池结构图
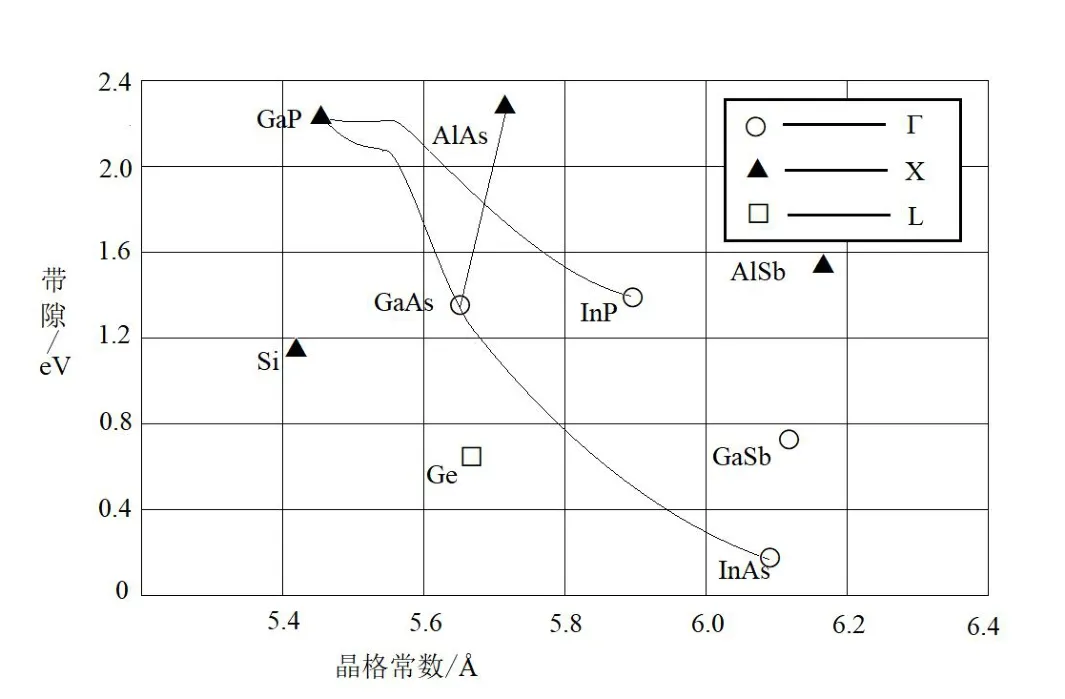
图2 Si、Ge 及III-V 族合金的晶格常数与带隙宽度之间的关系
本文重点讨论的GaInP/GaAs 叠层电池,因为是直接带隙,吸收系数高,很适宜于太阳电池。如带隙宽度为1.42eV 的GaAs,带隙宽度为1.85eV 的Ga0.5In0.5P 都是典型的例子。这种材料的n 型掺杂和p 型掺杂都很简单,并且用这种材料制备的复杂结构可以通过高产量的生产技术生长,同时保持非常高的结晶度和光电性能。因此,III-V 族电池是目前最高效率的单结电池,虽然这种单结电池效率仅比最好的硅电池略高一点,但是简单的制备方法使得效率超过30%的III-V 族的多结电池的制备成为可能,超过了任何的单结器件。
2 模型假设
我们给出简化的假设模型,包括:(a).透明的零阻抗的隧道结连接;(b).没有反射损失;(c).没有串联电阻损失;(d).结能收集每一个吸收光子,且电流-电压(J-V)曲线满足理想的二极管方程(n=1)。这种模型假设依据Kurtz S 和Wanlass M 等人的文献[3-4]。稍后我们会放宽假设(b),分析减反射膜的影响。
2.1 顶部和底部子电池的QE 和Jsc
通常情况下,顶部和底部子电池的短路电流密度Jsc取决于子电池的量子效率QE(λ)和入射到那个电池上的光谱Φine(λ):

基区厚度为xb,发射层厚度为xe,耗尽宽度为W(总的厚度x=xe+W+xb)的理想电池QE可以用标准公式表[5]述如下:
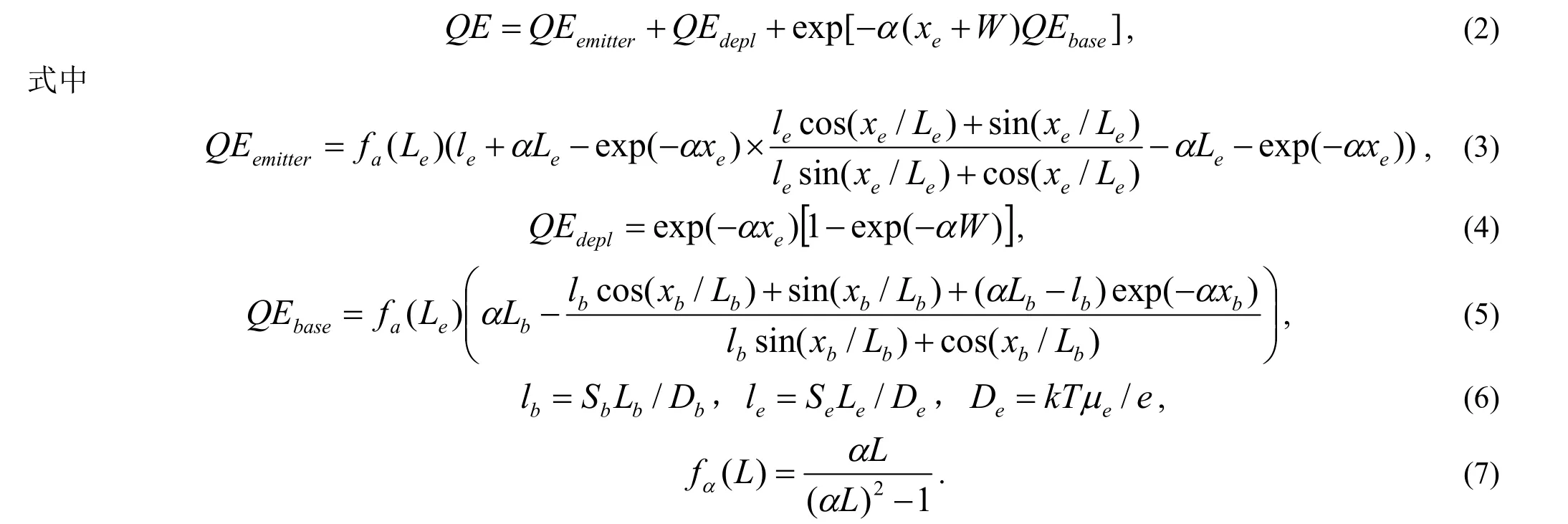
参数μb(e)、Lb(e)和Sb(e)分别是基区(发射区)中的迁移率、扩散长度和少数载流子表面复合速率;T是绝对温度。在本章的后面,我们将说明这个公式在分析真实的II-V 电池方面的作用。这里QE简单的取决于器件的总厚度x=xe+W+xb,即

假定底部的电池足够厚,足以吸收所有人射其上的大于带隙的光子,我们推断顶部电池的短路电流密度JSCt和底部电池电流密度JSCb为
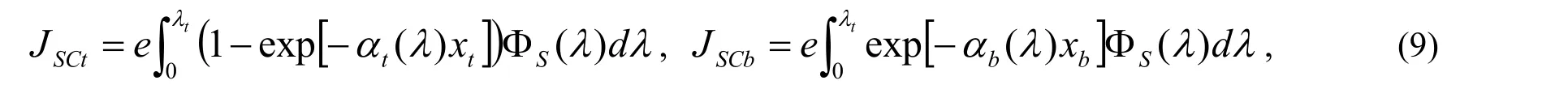
式中,λb=hc/Egb和λt=hc/Egt分别是底部和顶部电池带隙对应的波长。JSCb的积分下限是0,而不是λt,因为除非顶部电池无穷厚,否则总会有一些短波光子透射到底部电池上。因为底部电池经过了顶部电池的过滤,JSCb依赖于Egb和Egt,而JSCt只依赖于Egt。因此JSCt公式变为

2.2 多结电流-电压(J-V)曲线表达
对于任意m 级串联电池(或者任何一种两端子电池或者器件),第i个子电池的电流电压(J-V)曲线可简单描述为:

在给定的电流下电压等于所有在该电流下子电池电压和。每个独立的子电池都有自己的最大功率点{Vmpi,Jmpi}。但在多结串联电池中,通过每一个子电池的电流被迫具有相同值,因此只有每一个子电池的Jmpi都相同才会使每一个子电池都工作在最大功率点。这样这种多结器件的最大输出功率就是每一个子电池最大输出功率Vmpi Jmpi之和。如果子电池没有相同的Jmpi值,在组成的串联电池中一些子电池必然会偏离最大功率点运行。
图3 给出了串联J-V 曲线,包括一个GalnP 顶电池、一个GaAs 底电池和两结串联后的J-V 曲线。在这个例子中,设置底电池的Jsc 比顶电池的高,顶电池略微有分流,这是为了更容易看清串联后Jsc 的特性。

图3 两个子电池串联后(J-V)曲线的叠加(下图给出了叠层的Jsc 如何受限于电流较低的子电池。图中x 轴标出了当叠层电池的短路电流在14mA/cm2 时,顶电压和底电压)
为了定量的模拟多结器件,我们需要子电池的J-V曲线和Vi(J)表达式。用络想光敏二极管J-V方程(不考虑耗尽区)[5]:

实际中,Js/J0>>1,暗电流密度J0为

式中
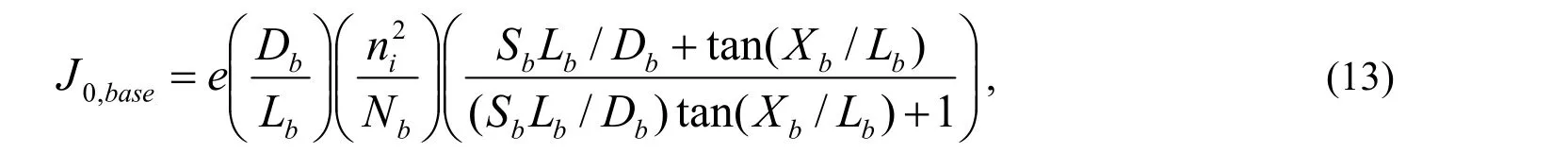
本征载流子密度公式ni由下式给出
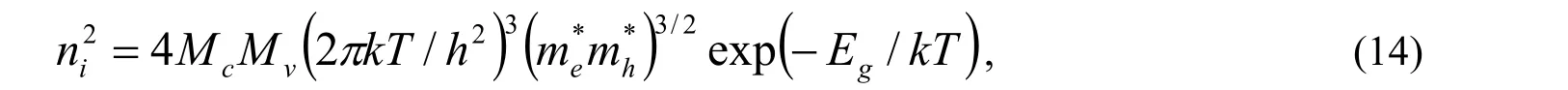
多结结构中的每一个结由式子(11)-(14) 描述;第i个结有暗电流J0短路Jsc等,及相应的J-V表征Vi(J)。这些独立结的Vi(J)曲线相加,得出多结V(J)曲线式(11)。最大功率点{Vmpi,Jmpi}可以在V(J)曲线上J×V(J)最大值处计算出来。
3 入射光谱的影响
为了得到确定的电池性能参数,我们需要选取多种结的材料。双结的n/p电池的合理的模型,除了带原是可变的之外,底部的结具有GaAs的特征。收系数一定是随着带隙的变化而变化的,光子能量小于带隙能量时吸收系数变为零。同样对于顶电池,模型使用GalnP材料特性,带隙也是可变的。
入射的光谱决定了光分配到每一个子电池的量,并相应的决定了每一个子电池产生的电流。因此,优化的带隙和顶电池厚度都取决于人射光光谱。图4c 给出了标准AM1.5D 下电池效率与顶电池和底电池带隙之间的关系,图4b 所用电池与图4c 一样,但是在AM1.5G 条件下。对于一个给定的底电池带隙,AM1.5D 光谱下的顶电池带隙Egt比AM1.5G 下低。这种不同是由于AM1.5D 相比AM1.5G 蓝光少,从而导致JSCt/JSCb减小;通过Egt的降低使更多的光入射到顶电池中从而弥补了这种降低。否则的话,对于给定的Egt和Egb,在AM1.5D 条件下顶电池厚度要比AM1.5G 的厚。图5d 给出了在{1.85 eV,1.42eV}的带隙对下JSCt、JSCb与顶电池厚度在AM1.5D 条件下的关系如图5a,只是图5a 是AM1.5G 条件下的,AM1.5D 条件下为满足电流匹配需要的厚度大约是1.2 μm,明显地比AM1.5G 条件下的0.7 μm 大。同样地,AM0 光谱比AM1.5G 有更多的蓝光,因此顶电池相应的更薄,厚度大约为0.5 μm。

图4 串联的两端子的双结叠层电池在不同子电池带隙下的效率等值线
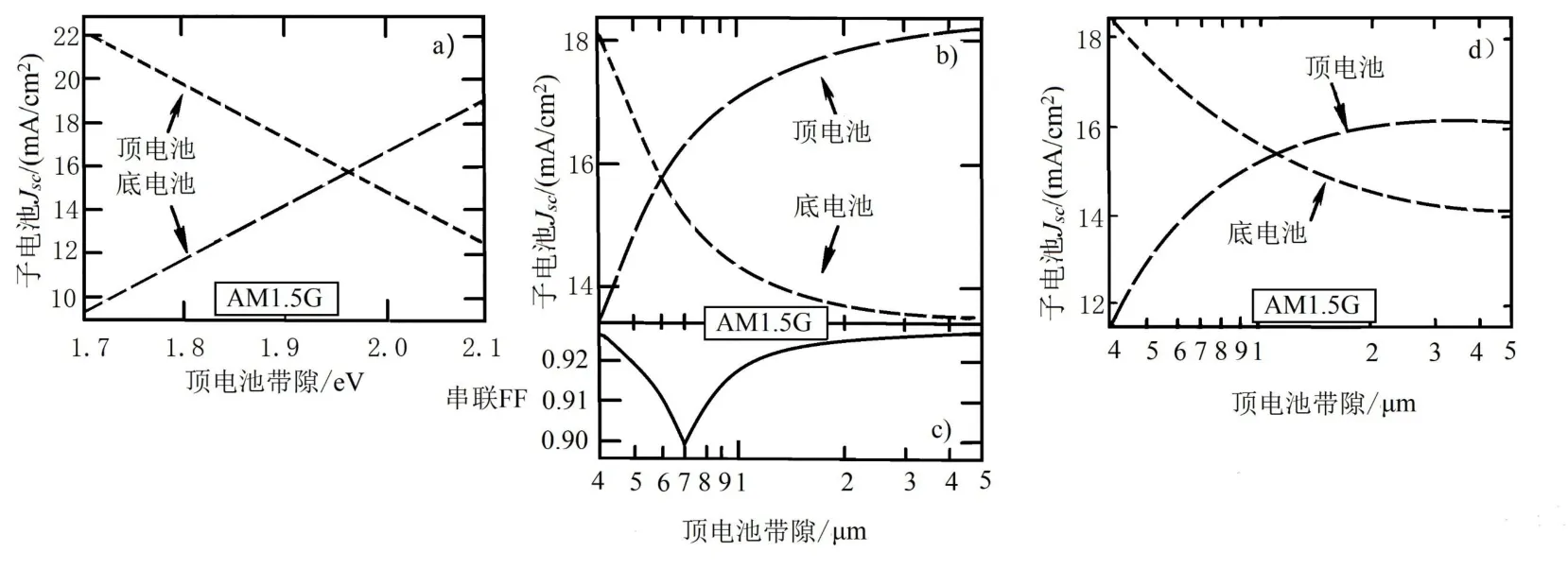
图5 a)在底电池带宽Egb=1.42eV 时顶电池厚度假设无限厚时,Jsct 和Jscb 与顶电池带宽Egt 的关系;b)在AM=1.5G 光谱下Egb=1.42eV、Egt=1.85eV 时,Jsct和Jscb与顶电池厚度的关系。电流匹配时厚度为0.7μm;c)相应的叠层电池的填充因子;d)在AM=1.5D 光谱下,其余条件同图b 时Jsct 和Jscb 与顶电池厚度的关系。此时电流匹配厚度比AMI.5G 光谱下的大得多
这里我们讨论分析了在给定光谱下如何选择顶电池的厚度,而实际情况是没有一个光谱可以准确的代表地面上太阳能电池接受的真实光谱,通常情况下,串联形式的叠层电池对大气质量的波动非常敏感,但是幸运的是在高空气质量下的效率相对不是很重要,这是因为在这种条件下的净输出功率小。
4 温度的影响
用基础电池公式(1)-(14)[6]来分析器件的温度是非常有用的,可以在合理的工作温度内预测器件的性能,并且对这些温度下测试出来的器件特性进行解释。我们将会看到串联多结电池中电流匹配限制效应对温度系数有影响,这在单结器件中是看不到的。
4.1 开路电压Voc
因为串联多结Voc是子电池Voc的简单相加,多结Voc的温度系数dVoc/dT 同样的是子电池的dVoc/dT 值相加。用GaInP/GaAs 串联电池作为例子,GaInP 和GaAs 子电池的dVoc/dT 都约为-2mV/°C。因此串联后dVoc/dT≈-4 mV/°C。表1 比较了几种电池的温度系数。由于低带隙的Ge 结的影响,可以看到GaInP/GaAs/Ge三结电池比GaInP/GaAs 两结电池有更负的1/VocdVoc/dT 值。然而在高聚光下1/VocdVoc/dT 的负值变小,随着聚光程度的增加Voc相应提高。

表1 多结和单结电池在300K 下的Voc 温度系数(假设结的品质因子n=1)
4.2 短路电流密度JSC
虽然串联多结电池的子电池的Voc温度系数是独立的可相加的,但多结电池的JSC温度系数要复杂得多。再用GaInP/CaAs 叠层电池为例,如前所述CaAs 子电池的JSC不仅取决于GaAs 带隙,同时还取决于GaInP 带隙,因为GaInP 子电池过滤掉了到达GaAs 子电池的光。当叠层电池温度上升,底部子电池带隙下降,其JSC趋向于升高,同时顶电池带隙也降低,这样减少了到达底电池的光,减小了底电池JSC随温度的增长。
叠层电池中的JSC受限于子电池中最小的JSC。通常,这些子电池的JSC不会有相同的温度系数。对于一个几乎是电流匹配的叠层电池,有一个交叉的温度,在此温度以下串联电池JSC受某个子电池的限制,在此温度之上串联JSC受另一个子电池限制。图6 给出了以GaInP/GaAs 为模型的叠层电池的交叉温度,在300 K时略微受到顶电池的限制。随着温度的升高顶电池JSC上升的比底电池快,当温度升至350K 之上时,出现了一个从顶电池限制转为底电池限制的转折。叠层电池的dJsc/dT 也出现了从Jsct/dT 向dJscb/dT 的转变。

图6 a)子电池和相应的叠层电池的JSC 随温度的变化,GaInP/GaAs 叠层电池在300K 的温度下受限于顶电池;b)相应的dJsc/dT,当电池温度高于340K,电池由受限于顶电池转变为受限于底电池,并且dJsc/dT 发生相应改变;c)填充因子的温度系数dFF/dT;d)效率随温度改变dFFff/dT/
叠层电池的填充因子取决于对电流起到限制作用的那个子电池,所以dFF/dT 与dJs/dT 的转折点类似,在图8c 中顶电池限制向底电池限制的转变导致dFF/dT 的变化。效率与Voc×Jsc×FF 成比例,并且在通过交叉温度时,dJsc/dT 和dFF/dT 变化趋势相反,所以dEff/dT 随温度的变化较为平滑。
5 结论
通过建立顶部和底部短路电流密度Jsc和子电池的量子效率QE(λ)模型画出了子电池的J-V曲线,建立Vi(J)表达式后,计算了最大功率点{Vmpi,Jmpi},最终从入射光谱和温度两个方面分析影响因素,在带隙选择和相应结构下的效率预测方面给出依据,为多结串联器件的定量理解及定量设计提供基础。

