金属蜂窝夹芯结构抗水下冲击性能

李汶蔚，黄 威

（1. 中国原子能科学研究院，北京 102413；2. 华中科技大学船舶与海洋工程学院，湖北 武汉 430074）

在水下爆炸冲击载荷作用下，舰船局部防护结构的响应是一个高度非线性动力学过程，涉及流固耦合、断裂力学、塑性动力学等多个学科。舰船材料创新、优化船体结构及关键部位的抗冲击性能是目前船体防护性能研究的主要方向[1]。与单层板相比，夹芯结构具有轻质、比刚度大、比强度高、能量吸收性能和隔声隔热性能优越等特点[2]，在冲击载荷作用下，其缓冲性和抗穿透性也具有明显优势[3-6]。相较于其他复合材料结构[7-8]，拓扑芯材金属夹芯结构在准静态、抗侵彻以及爆炸性能研究等方面已取得了丰富的研究成果。近年来，金属夹芯结构也因其缓冲吸能优势广泛应用于航空、航海领域。

为了进一步开展水下防爆结构研究，Fleck 等[2]在Taylor[9]一维水下冲击波理论的基础上，设计了模拟远场水下爆炸的高强度水下冲击加载装置，通过该装置可产生与水下爆炸相似的加载脉冲信号。基于该加载装置，水下冲击载荷作用下金属夹芯结构的动态响应和失效机理研究获得了重大进展。Fleck 等[2]将冲击载荷作用下的夹芯结构响应分为流固耦合阶段、芯材压缩阶段和结构响应阶段3 个阶段，并预测了夹芯结构的变形模型。后续，研究人员通过一系列实验、数值模拟和理论分析对该结构动态响应模型进行修正[3,10-12]，通过对3 个阶段的耦合和解耦，逐步深入揭示该结构的响应机理。国内学者Qin 等[13]和Cui 等[14]对空气爆炸下芯材强度对解耦响应的影响进行了研究；Huang 等[15-17]采用不同水下爆炸模拟装置对多种芯材结构开展理论和实验研究。理论研究主要是分析芯材结构的变形机制，并且均基于解耦分析获得；实验研究则由于测试手段所限，很难获得完整的结构响应参数。因此，通过数值模拟手段进一步揭示水下冲击载荷作用下芯材结构的抗冲击特性十分必要。

本研究在已完成的实验研究基础上，采用全尺寸三维数值模拟方法开展了金属蜂窝夹芯结构在高强度水下爆炸模拟装置加载下的动态响应和抗冲击特性研究。通过改变蜂窝夹芯结构的相对密度，研究了不同冲击载荷和芯材相对密度影响下夹芯结构的抗冲击特性，并与相应的实验和理论模型进行对比。

1 数值分析模型

通过数值模拟方法对文献[18]的实验结果进行深入分析，利用ABAQUS/EXPLICIT 建立了如图1所示的基于拉格朗日方法的三维数值分析模型，模型所有尺寸与实验保持一致。高强度水下冲击加载模拟实验装置主要由图1（a）所示的一级轻气炮系统和圆桶状激波管组成，通过轻气炮发射高速飞片与激波管前置活塞平面撞击，在激波管中形成一系列平面冲击波，冲击波由激波管前端传播到尾端。这种可控性强、强度高的水下冲击波使得在实验室开展夹芯结构的抗水下冲击性能研究更为方便[19-20]。该加载装置的有效性已经被大量学者证实[8,16,19-20]。

图1 高强度水下冲击加载实验装置示意图（a）和数值分析模型（b）Fig. 1 Intensive underwater explosive simulator (a) and the numerical model (b)

该模型采用的飞片和前置活塞厚度分别为8.1 mm 和12.0 mm，质量分别为0.22 kg 和0.31 kg。实验过程中，飞片的初始速度vf为20～220 m/s，通过压力传感器测得水下脉冲峰值强度为10～300 MPa。靶板的有效加载面是一个直径（2L）为 66 mm 的圆。金属蜂窝夹芯结构的蜂窝芯材为六边形蜂窝芯子，壁厚为0.01 mm，横向厚度为10 mm，材料为3003H18 铝合金；前后面板厚度相同，均为0.5 mm，材料为5A06 铝合金。考虑应变率效应的两种铝合金材料基于Johnson-Cook 模型的材料性能参数见表1。加载应变率为7.41 × 10−4s−1，横向屈服强度为1.92 MPa，压实应变为0.54。设计了4 种不同相对密度的蜂窝夹芯结构进行数值模拟研究，通过将蜂窝芯子的单胞边长a分别设置为4、6 和8 mm实现不同的结构相对密度，蜂窝单胞的其余尺寸一致。其中，通过多组重复实验得到的典型蜂窝夹芯结构（a= 4 mm）在准静态压缩下的应力-应变关系如图2 所示。

为了简化分析过程，忽略压力波传播过程中水容器及活塞可能与水发生的流固耦合现象，采用无摩擦的接触算法。在流体和结构接触处，由于压力降低在流固界面处易形成空化效应。为了模拟空化现象，水单元采用C3D8R 单元。在水下冲击作用下表现为线弹性，并设置其对应的拉伸及剪切强度为零。为了不影响冲击波在水下的传播，水的横向单元尺寸必须受到严格控制。设置沿波为传播方向上水的单元尺寸为0.2 mm，径向尺寸为0.4 mm。将飞片、活塞和水容器均设置为刚体。在单层5A06 铝合金靶板抗冲击实验中，靶板单元同样采用C3D8R 单元。在受冲击区域环向单元尺寸为0.4 mm，沿厚度方向为3 个单元。为了与实验一致，靶板背面用完全固定边界条件的刚性金属圆环对靶板进行固定。

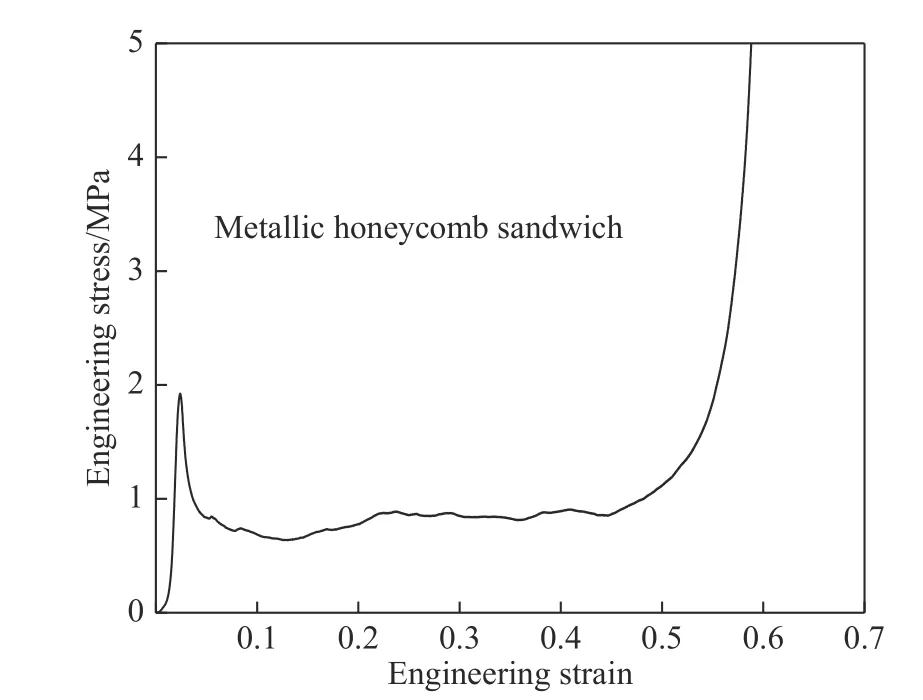
图2 蜂窝夹芯结构准静态压缩下的应力-应变关系Fig. 2 Stress-strain relationship compression of honeycomb sandwich structure under quasi-static compression

金属蜂窝结构面板和芯材均采用Johnson-Cook 本构模型，模型参数见表1。二者的失效模型均采用延性失效模型，假设累计等效塑性应变达到临界值时材料开始失效。水的模型采用线性Hugoniot 形式的Mie-Grüneisen 状态方程，其参数见表2，其中水下声速由实验结果测得[21]， γ为Grüneisen 常数。

表 1 面板和芯材材料力学性能参数Table 1 Mechanical parameters of aluminum materials

表 2 Mie-Grüneisen 状态方程参数Table 2 Parameters for the Mie-Grüneisen equation of state

2 数值模型有效性验证

为了验证数值分析模型的有效性和准确性，对文献[18]中蜂窝单胞边长为4 mm 的蜂窝夹芯结构实验结果进行对比。为了与实验结果保持一致，本研究采用无量纲冲量表示加载强度

式中：It为透射脉冲强度，L为靶板半跨长度，ρf和σf分别为面板的密度和强度。进行无量纲变形

式中：w为横向变形大小，t为结构响应时间。

图3 展示了蜂窝夹芯结构在受到初始速度为48.0 m/s 的飞片撞击时，产生无量纲冲量=2.68 时，实验和数值模拟得到的失效模式对比。由图3 可知，数值模拟结果与实验结果具有较好的一致性，包括失效发生的位置和分布，以及涉及单胞屈曲的失效模式。随着冲击强度发生变化，芯材的压缩也随之变化，伴随结构响应的变化。

图3 实验和数值模拟的失效模式对比Fig. 3 Comparison of the deformation modes obtained from the simulation and experiment

图4（a）为蜂窝结构在不同冲击强度下背板中点的响应时程曲线。随着冲击强度增加，中点响应速度明显增加，蜂窝结构发生更大的塑性变形。尽管数值模拟的响应速度比实验结果更大，但是二者的中点最大变形相近。在数值模拟分析中，假设水下压力为零即发生空化，结构发生横向变形导致空化出现，这两个阶段的解耦现象较为清晰，空化出现的位置均位于流固界面处。在实验加载过程中，由于流固耦合效应，流固界面处的空化演化更为复杂，空化出现的位置和时间均与数值模拟存在差异。这种简化的数值模拟分析是响应时间不同的主要原因。背板中点变形随冲击强度变化的总体趋势与实验结果有较好的一致性，并且与Fleck 等[2]采用的外包法理论分析结果较为吻合，如图4（b）所示。因此，该数值模型能够较为准确地模拟蜂窝夹芯结构在水下冲击载荷作用下的动态响应。

图4 蜂窝夹芯结构背板中点变形时程曲线（a）和最大变形与冲击强度的关系（b）Fig. 4 Mid-point deflection history of honeycomb sandwish structure (a) and relationship between impulsive intensities and maximum deflection (b)

3 蜂窝夹芯结构抗水下冲击性能分析

3.1 结构动态响应

图5 为数值模拟得到的胞元边长为4 mm 的蜂窝夹芯结构在水下冲击载荷作用下横向变形的动态过程以及对应前面板上塑性铰的运动。对比实验和模拟得到的蜂窝结构失效模式发现：冲击强度较小时不足以驱动前面板的塑性铰运动至终点，最大变形以平台值的形式显现在面板的中心区域，如图3所示的实验结果，对应图5 中0.40 ms 时的作用结果。芯材的中心区域整体横向移动，两侧芯材胞元由边界向中心发生胞元渐进形式的屈曲。增加冲击强度，前面板以初始速度继续运动，在0.44 ms 时两侧塑性铰汇聚于中点并继续横向运动。动态塑性铰链的运动及失效模式与实验结果有较好的一致性[18]。

图5 蜂窝夹芯结构在1 = 3.58 作用下的等效应变分布和塑性铰运动Fig. 5 Dynamic deformation and propagation of plastic hinges of the honeycomb sandwich，1 = 3.58

Tilbrook 等[22]通过夹芯结构前后面板的速度响应过程反映不同芯材强度金属夹芯结构在受到冲击载荷作用时的变形机制，并将其按芯材的强度区域将金属夹芯结构的变形机制分为4 类。图6所示为夹芯结构在1 03It= 4.28 时前后面板中点的速度响应过程。在冲击的初始时刻，前面板获得速度v0，并在芯材和背板的作用下开始减速，与此同时背板在芯材作用下开始加速；在时刻teq二者获得共同速度；之后，二者同时开始减速运动直至速度为零。由此判定含两种面板结构的芯材为高强度芯材。结合Tilbrook 等[22]的结果与本研究的数值模拟结果可以看出，在不高于图6 所示的冲击强度时，前、后面板在芯材未发生完全压实时已经获得共同速度。

图6 蜂窝夹芯结构前后面板中点的速度响应过程Fig. 6 Velocity time history at the mid-point of front and back face-sheet of honeycomb sandwich structure

3.2 芯材相对密度效应

选用面板相同、蜂窝单胞边长不同的夹芯结构，对比分析芯材相对密度对结构抗冲击性能的影响，单胞边长分别为4、6 和8 mm。采用无量纲质量=mc/m（mc为芯材质量，m为结构总体质量）。图7为不同相对质量芯材的蜂窝夹芯结构受到相同冲击载荷作用时的等效塑性应变分布。当芯材的相对质量较低时，其失效机理主要为面板的拉伸和蜂窝单胞壁的屈曲；而当mc= 0.21 时，蜂窝芯材的失效除了单胞壁的屈曲外还有纵向的拉伸失效。这种纵向拉伸由外侧向中心逐渐增大，当冲击强度不断增加，芯材首先在中心位置发生局部压实和完全压实的失效模式。芯材相对密度变化呈现出的不同的芯材失效模式说明了芯材密度对结构响应的重要作用，进一步可表现为其抗冲击性能的差异。

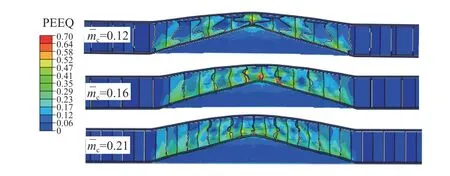
图7 相同冲击强度下不同芯材相对密度的蜂窝夹芯结构等效应力分布Fig. 7 Equivalent strain distribution of honeycomb sandwich under the same impact loading

3.3 抗冲击参数分析

在实验结果的基础上，利用建立的有效数值模型，通过改变响应夹芯结构芯材的相对密度可以获取更多的有效参数以评估结构的抗冲击性能，进而通过得到的趋势获取该抗冲击参数与冲击强度及相关几何特性间的量化关系，最终通过优化参数获得性能更好的结构。对于受到爆炸载荷加载的结构，可主要通过背板的中点横向变形w、结构固支端反力FR、透射脉冲强度IT以及塑性能耗EP等几个方面对金属夹芯结构在水下冲击载荷作用下的结构响应和能量耗散机理进行对比分析，从而评估其抗冲击性能。结构-载荷-性能的关系[8]可直观反映结构的抗水下冲击性能，即抗冲击参数Z(w、FR、IT、EP)、相 对质量x(mc)和脉冲加载强度y(It)之间的量化关系

式中：K、m、n分别为拟合参数。

通过数值仿真分析，得到图8 所示的不同相对密度蜂窝夹芯结构在冲击强度发生变化下的无量纲变形。与图4 相似，随着冲击强度增加，结构变形程度增大。在相同冲击强度下，中点变形随着芯材相对密度的降低而增加。通过式（4）对结果拟合，得到数值模拟后的横向变形和冲击强度，结构参数间的量化关系

利用反力计算得到夹芯结构在不同强度水下冲击载荷作用下透射到固支端的脉冲强度。如图9所示，结构固支端反力时程曲线的变化趋势与冲击强度和芯材相对密度无关，幅值随冲击强度的增加而增大，随芯材相对密度的增加而降低，在单一冲击强度或芯材相对密度影响下结构有明显的反力差异。因此，夹芯结构受到水下冲击载荷作用后，作用于固支端的反力受到芯材相对密度和冲击强度的影响较大，在评估结构的抗冲击过程中，需要将相连结构形成的反力作为重要因素进行考虑。与相同单位面积质量金属单层板的反力对比，二者呈现明显不同的趋势，单层板的反力峰值大且持续时间长。

图8 蜂窝夹芯结构横向变形与冲击强度及芯材相对密度的关系Fig. 8 The relationship of transverse deflections for honeycomb sandwich structure load intensity and relative core density

图9 夹芯结构支座的反力时程曲线Fig. 9 Reaction forces time histories for sandwich panels

图10 夹芯结构透射脉冲强度与冲击强度及几何特性的关系Fig. 10 Relationship of transmitted impulses to incident impulse intensity and geometries

图10 为反力积分得到蜂窝夹芯结构的透射脉冲强度、冲击强度和芯材相对密度的关系，其变化趋势与反力趋势相同。芯材相对密度最小时无量纲透射脉冲最大，冲击强度最高时透射脉冲最小。对计算结果进行拟合，得到数值模拟下的横向变形和冲击强度、结构参数间的量化关系

分析夹芯结构面板和芯材在结构受到冲击载荷作用下发生变形和失效过程中塑性能的耗散比例，对于分析芯材和面板对结构的防护性能有着十分重要的作用。对夹芯结构而言，塑性能的无量纲形式为

式中：Ep为直接获取的结构消耗的塑性能，A为加载区域面积，mz为结构整体的单位面积质量。根据数值模拟结果，结合不同结构组成部分的塑性能量耗散时程曲线，从式(7)可得到相应的量化关系。

图11 所示为冲击载荷作用下蜂窝夹芯结构各部分以及总体塑性能耗时程曲线。由图11 可知，前面板和芯材的初始响应时间基本同步，背板的响应时间明显大于二者。前面板的初始运动使得芯材整体迅速发生压缩和屈曲，面板发生拉伸和弯曲。在经历相同初始增长速率后，芯材的塑性能耗增长速率明显高于前面板的增长速率，进而使得在较低冲击强度下，芯材的最终塑性能耗高于前面板的能耗。但是，随着冲击强度增加，芯材发生压实或者局部压实失效后，前面板的能耗增长速率又超过了芯材，并最终发生最大的塑性变形。对于拓扑结构和几何尺寸不同的夹芯结构，其前面板获得最大塑性变形的临界冲击强度各不相同。由模拟结果可知，芯材相对密度降低导致该临界冲击强度降低。由于前面板和芯材消耗了塑性能，背板发生的塑性变形始终最小。这种特点使得总体塑性能耗不像前述几种抗冲击参数随冲击强度和相对密度呈现单调变化，而是表现为：在相同冲击载荷作用下，不同芯材密度引起的单位塑性能耗变化微小；随着冲击强度增加，由于其耗能机理不同，相同结构的塑性能耗出现降低，但整体塑性能耗仍然随冲击强度增强而增加。拟合得到塑性能耗、冲击强度和相对密度的量化关系

图11 蜂窝夹芯结构各部分的塑性能耗时程曲线(a)及塑性能耗与冲击强度和芯材相对密度关系(b)Fig. 11 Plastic dissipation histories at different places of honeycomb sandwich structure (a) and the relationship of plastic dissipations to incident impulse intensity and relative core density (b)

4 结 论

对比实验与数值模拟结果和经典的金属夹芯结构动态响应理论，三者有较好的一致性。在结构发生完全失效前，主要由面板拉伸和芯材压缩引起了一系列失效模式。芯材的屈曲从边界到中心呈现渐进型，随着冲击强度增加，芯材首先在中心位置发生局部压实和完全压实的失效模式。获得了冲击强度、芯材相对密度对水下冲击载荷下蜂窝夹芯结构横向变形、反力、透射脉冲以及塑性变形能耗几种抗水下冲击参数的结构、载荷、性能的影响规律与量化关系。