直觉梯形模糊TOPSIS 在校企合作模式决策中的应用
周卫标
(广东邮电职业技术学院 经济管理学院,广东 广州 510630)
近年来,随着校企合作培养人才模式在全国普通高等学校的推广与深化,大部分的高校均与企业开展不同规模和不同形式的校企合作,在人才培养方面取得一定的创新,校企合作取得一定的成效。很多学者致力校企合作的研究,并且取得了众多的研究成果。南旭光等认为开展校企合作,有利于培养高素质和精技术的技能型人才,可以促进产学融合发展,顺应现代化教育发展的基本要求[1]。王慧英等提出校企合作可以充分发挥企业的优势,能够让高等学校与企业间的价值得到充分体现,实现应用型大学与市场的有效对接[2]。在校企合作评价指标体系以及评价方法的确定上,学者也做了大量的研究。文益民等在校企合作综合评价中主要考虑了校企合作基础、校企合作设计、校企合作实施、校企合作效果4 个评价指标[3]。程晓静等构建了校企合作投入、校企合作过程、校企合作结果为指标的评价指标体系,并采用了FEAHP 方法对校企合作绩效进行评价[4]。李兰军以资产投入、资源管理、合作成果、社会效益为评价指标探讨校企合作评价,通过模糊综合评价法确定校企合作评价等级[5]。Atanassov 首次提出直觉模糊集的概念,增加了非隶属度函数,是一种犹豫不决的、中立的状态[6-8]。Hatami 等采用了直觉梯形模糊TOPSIS 对股票市场交易应用进行综合评价并做出决策[9]。陈晓红、周晓辉、宝斯琴塔娜等运用梯形模糊TOPSIS 进行评价与多属性群决策[10-12]。江登英等针对属性权重和专家权重全部未知的三角模糊数多属性群决策问题,在三角模糊数熵的基础上构造了确信度指标来量化对决策信息的信任程度,提出了基于三角模糊数确信度算子的属性信息集结新方法[13]。
1 直觉梯形模糊TOPSIS
设A是实数集R上的直觉梯形模糊数,参数为a1≤a2≤a3≤a4,计作A=(a1,a2,a3,a4)则其隶属度函数和费隶属度函数定义[10]为:
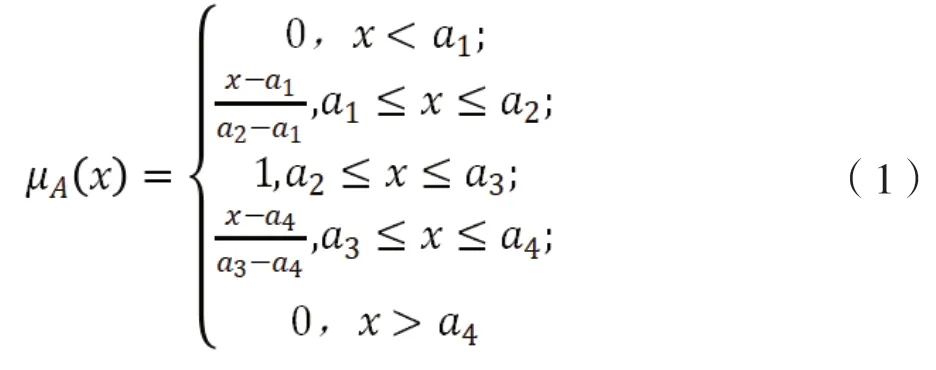
设A1=(a11,a12,a13,a14) 和A2=(a21,a22,a23,a24)是两个直觉梯形模糊数,则梯形模糊数的基本运算规则:

计算两个梯形模糊数之间的距离用公式如下:

k位专家给出模糊指标权重和模糊方案等级可以表示为和。方案等级的综合模糊值可通过式(6)进行计算[9]:

另外,综合模糊权重值可以用式(8)表示:

然后模糊方案等级值和模糊权重值可以通过一个模糊决策矩阵来表示:

为了避免计算繁杂,对模糊决策矩阵进行标准化处理,使决策矩阵具有同质性。标准化模糊决策矩阵表示如下:

当指标为效益型指标和成本型指标时,分别表示为:
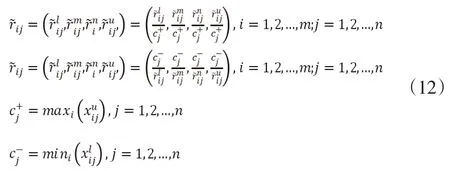
加权的标准化模糊决策矩阵可以通过式(13)、式(14)进行计算:

正理想解和负理想解可以通过式(15)、式(16)计算:

多个备择合作模式到正理想解和负理想解的距离通过式(17)计算:

计算各备择合作模式的相对接近度,并对其大小进行排序,相对接近度越大说明越接近理想点,则可以做出决策,选择最优合作模式:
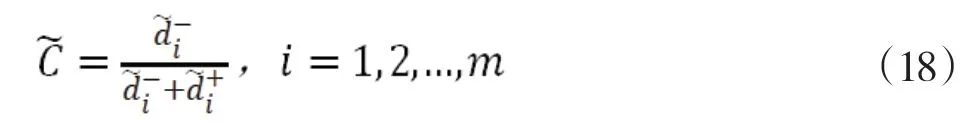
2 算例
广东省某职业院校物流管理专业非常注重校企合作,建立多个校内和校外的实习和实践基地。目前和某公司洽谈校企合作,该公司共提供订单班、巅峰实习和寒暑假实习三种的校企合作模式。订单班实习期间为学生从大三第一学期开始连续3 个学期,每学期大概6 周时间到该公司物流岗位进行轮岗实习。巅峰实习是指“双十一”和“6.18”等巅峰作业期间,在物流岗位的实习,没有轮岗。寒暑假实习主要为寒暑假期间到物流岗位实习,也没有轮岗。学校领导高度重视与该公司的校企合作,建立5 人的专家小组对三种校企合作模式进行评价,然后利用直觉梯形模糊TOPSIS 选择学校发展和专业建设发展相适应的合作模式。
首先,构建校企合作模式评价指标体系。通过参考前人在校企合作模式评价的研究成果[3-5],同时根据学校的招生就业情况以及以往校企合作的经验,结合合作企业的合作模式特点,专家小组选定了学校教育教学改革、双师型专业教师培养、企业参与人才培养方案制定、学生技能提升和职业技能证书、学生管理5 个指标构建评价指标体系。其中学校教育教学改革是从学校的教育教学发展层面考虑,双师型专业教师培养是从教师队伍建设层面考虑,企业参与人才培养方案制定是从企业合作以及人才培养层面考虑,学生技能提升和职业技能证书和学生管理是从学生能力提高及学生管理层面考虑。构建的评价指标体系全面考虑学校、教师、企业、学生层面,具有全面性和科学性。
然后,运用直觉梯形模糊TOPSIS 方法对校企合作模式进行选择评价,评价的过程与步骤如下:
第一步:5 个专家参照表1[9]对合作模式的5个评价指标进行比较并写出语言评价,假设各专家有相同的权威性,再根据集成算子方法式(8)、式(9)得到综合模糊权重值,如表2 所示。

表1 权重语言变量和梯形模糊数

表2 专家对指标权重的语言评价与综合模糊权重值
第二步:假设5 个专家具有相同的话语权,5 位专家参照表3[9]的语言变量及其梯形模糊数,对3 个合作模式进行评价,得到评价语言变量如表4 所示。
根据公式(12)对综合模糊决策矩阵进行标准化处理,通过式(13)、式(14)进行加权处理,得到加权综合模糊决策矩阵见表5。
第三步:通过式(15)、式(16)运算得到模糊正理想解和负理想解。对指标进行分类,通过指标的性质看出指标都为效益型指标。根据效益型指标的计算公式,得到模糊正理想解和负理想解为A+和A-,并得到各备择合作模式的指标到正负理想解的距离,根据式(17)、式(18)得到各校企合作模式与模糊理想解的相对接近度如表6 所示。
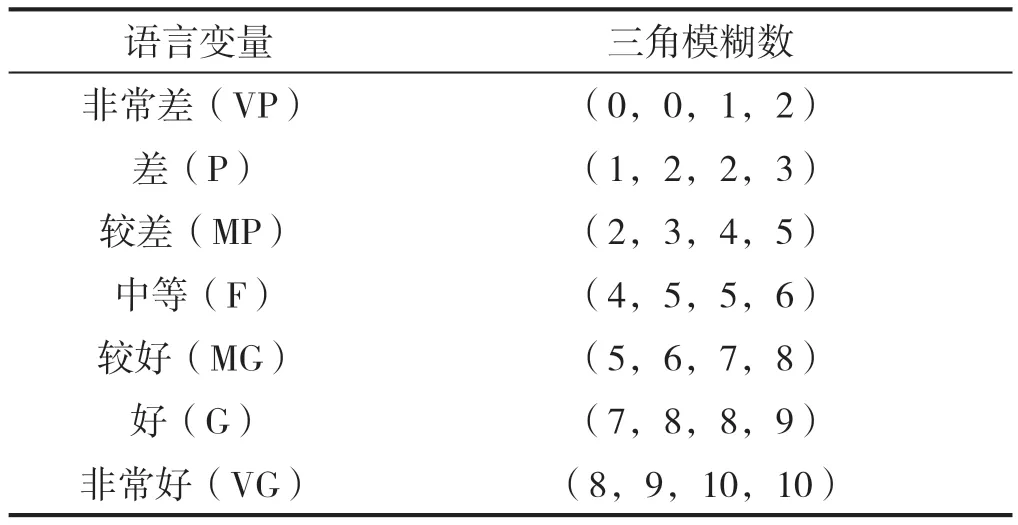
表3 评级语言变量和梯形模糊数

表4 专家对合作模式的语言评价

表5 加权标准化综合模糊判断矩阵
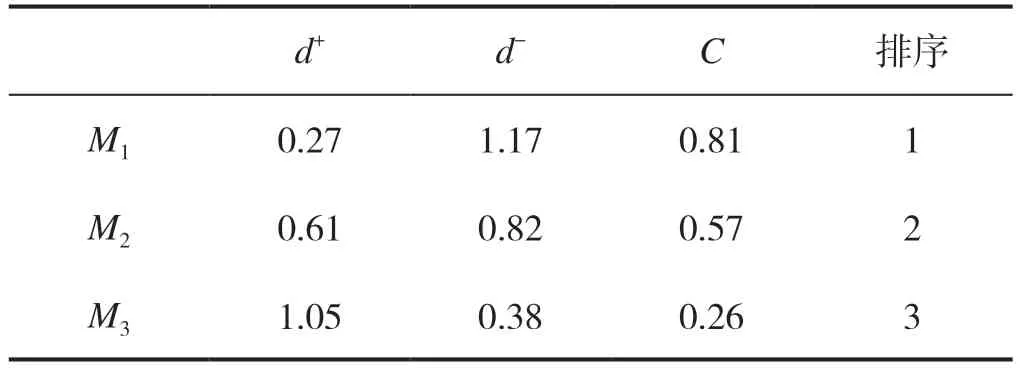
表6 合作模式到正负理想解的距离及相对接近度
从表6 综合评价指标结果能够得知,3 个备择校企合作模式的优劣排列顺序为:M1>M2>M3。M1(订单班)合作模式的综合得分为最高,因此可以得到M1为最优合作模式,校方可以与选择M1模式与企业建立校企合作。
3 结论
随着校企合作在高等学校的日益深入开展,合理的校企合作模式选择变得愈加重要,校方越来越重视对校企合作模式选择评价的科学合理性。运用直觉梯形模糊TOPSIS 方法,基于校方的角度对校企合作模式进行客观评价,有利于学校选择最优的合作模式,有利于学校在校企合作中健康有序发展。通过算例可以看出,构建的评价指标体系和应用的评价方法对校企合作模式进行评价,具有方便、简单的特点,客观性和科学性也更强。

