采用不同监测数据组合反演饱和均质石英砂水热运移参数

潘梦绮，黄权中，冯 榕，黄冠华

·农业水土工程·

采用不同监测数据组合反演饱和均质石英砂水热运移参数

潘梦绮，黄权中※，冯 榕，黄冠华

（1. 中国农业大学中国农业水问题研究中心，北京 100083；2. 中国农业大学中国-以色列国际农业研究培训中心，北京 100083）

土壤及含水层的水力参数与热参数对于定量描述土壤水、地下水迁移规律及其伴生的热运移过程十分重要。为探讨不同监测数据类型组合对多孔介质水热参数估计的影响，该研究基于热示踪方法，开展了3种不同粒径条件下的饱和均质石英砂的热示踪试验，并结合HYDRU-2D模型对介质的饱和导水率、导热系数和纵向、横向热弥散度进行反演。参数估计时分别设置3种情景对介质水热参数进行估计：仅采用观测点温度（R1）、观测点温度+水流通量（R2）、观测点温度+水流通量+热量损失（R3）。并对R1情景设置3种不同参数反演组合，即同时对2组参数（饱和导水率和导热系数）、3组参数（饱和导水率、纵向和横向热弥散度）和4组参数（饱和导水率、导热系数、纵向和横向热弥散度）进行估计。研究结果表明：同时对介质饱和导水率、导热系数与热弥散度进行估计，有利于提高介质水热参数的估计精度；对导热系数的合理估计可减小R1情景中介质饱和导水率的估计误差。4组参数中饱和导水率是敏感性最高的参数，增加用于参数反演的水流运动和热量传递信息时，粗砂、中砂、细砂的累积流量相对误差分别减少了9.74、6.65和12.53个百分点，显著提高了介质饱和导水率的反演精度。饱和导水率的估计值随介质粒径增大而增大，而纵向热弥散度随粒径的变化则呈相反的变化规律，横向热弥散度估值基本不变。增加水流和热量传递信息还能显著提高中砂的导热系数反演精度，导热系数的估计值随着介质孔隙度增大而逐渐降低。研究可为基于不同数据类型的均质介质参数反演提供。

数据；参数；热示踪；饱和石英砂；水热运移模型；HYDRUS软件

0 引 言

土壤和地下含水层中的水分与热量迁移在农业生产、地下水污染评价等方面具有重要意义[1]。其中，多孔介质水力参数与热参数的确定，对于定量描述土壤水、地下水运移规律及其伴生的热迁移规律十分重要。在工程实际中，渗流介质和边界条件往往都比较复杂，利用解析公式求解渗透系数或渗透张量则更加困难，因此数值模拟方法逐渐成为了研究饱和/非饱和多孔介质中水热迁移规律的重要手段。

传统测量渗透系数的方法有经验公式法、室内试验法、野外抽水实验、压水实验法、数学模型反演计算法等[2-6]。温度采集设备的智能化发展使得利用温度数据来补充和替代测压管水头并分析多孔介质流场及其水力特性成为可能。大量的研究表明，热示踪可在一定程度上较准确对介质的水、热参数进行反演[7-11]。并且在利用温度数据反演参数的基础上同时考虑其他不同类型的数据信息，有利于提高参数估计的精度。Nakhaei等[12]采用HYDRUS模型对土壤温水入渗过程进行模拟，结果表明利用多种反演数据可以获得具有较高精度的水热估计参数。Giambastiani等[13]则将相同水力条件下的溶质迁移和热示踪试验相结合，达到了准确估计纵向热弥散的目的。近年来，为获得更准确的非均质介质的渗透系数分布，断层扫描也逐步应用于热示踪试验中[14-15]。

本文采用3种不同颗粒尺寸的石英砂分别开展了饱和稳定流场条件下的均质介质的热示踪实验，并结合HYDRU-2D模型对介质的水热参数进行反演。参数估计时设置了3种不同类型数据的反演情景，利用不同类型的数据信息对介质的水热参数进行估计，并分析数据类型对参数估计的影响，从而获得基于热示踪的饱和均质介质水、热参数反演方法。

1 材料与方法

1.1 试验装置

本文构建了基于饱和多孔介质水热运移过程的热示踪试验平台，分别由进水装置、有机玻璃砂箱、数据采集装置及出水装置4部分构成，如图1所示。

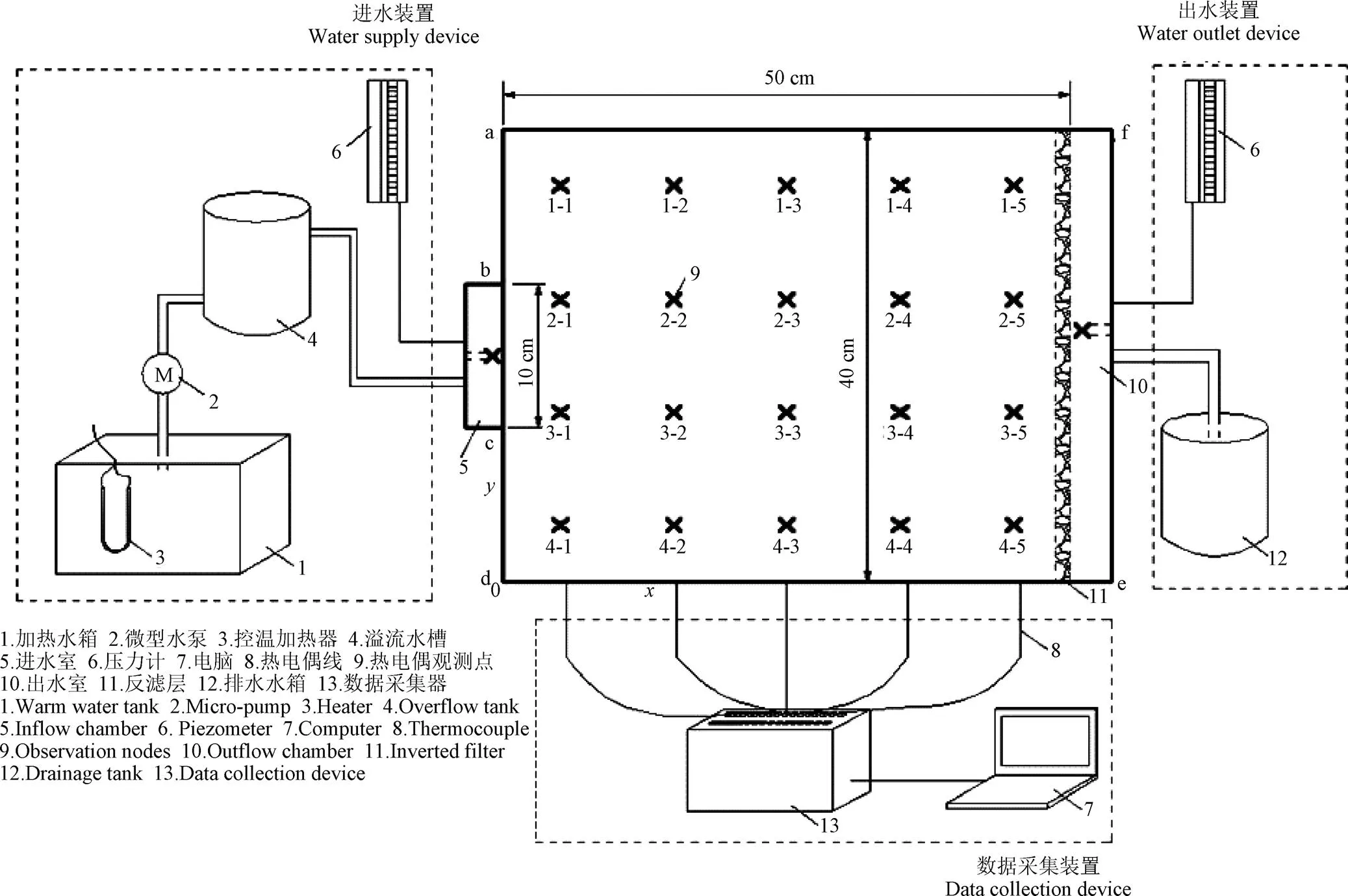
图1 热示踪试验装置示意图

有机玻璃砂箱的长、宽、高分别为50、40、2.5 cm。砂箱左侧中部为进水室，长为10 cm；右侧全部边界为出水室，长为40 cm。分别在进、出水室和石英砂介质间设置厚度为5 cm的多孔隔板和反滤层，从而防止细小的石英砂堵塞多孔隔板。在砂箱背面均匀设置20个热电偶观测点，分别在进、出水室底部设置2个热电偶观测点。T型热电偶线（美国Omega工程公司，0.01 ℃）一端埋设于介质内部，一端与CR3000型数据采集器（美国Campbell科技公司，3次/min）相连。进水装置由溢流水槽、加热水箱及微型水泵组成。溢流水槽连接砂箱进水室为试验提供恒定水头；采用控温加热器为试验提供恒温热源；出水室连接排水水箱，并且进、出水室均安装压力计。

试验采用3种不同粒径的白色精制工业石英砂，砂箱从进水口到出水口分层填装，介质的饱和含水率与导热系数均通过一维均质砂柱试验获得，如表1所示。

表1 石英砂的基本物理性质

1.2 试验方法

试验开始前在恒定水头条件下先注入常温水（23 ℃），当出水流量稳定和各观测点温度不再变化后，保持水头不变，将恒温水流（45 ℃）通过溢流水槽立即注入进水室。试验采用热电偶对石英砂内部温度进行监测，测量频率为1次/min。试验过程中分别对进、出水室的压力计读数和排水箱累积出流量进行测定。当砂箱内各观测点温度均达到稳定不再变化后，试验结束。当砂箱冷却至常温，保持该试验水头恒定，重复试验。

1.3 介质水热参数反演

1.3.1 二维饱和介质中水、热运移控制方程

本文采用HYDRUS-2D软件对饱和稳定流条件下的介质水、热迁移参数进行反演。二维饱和介质中水流运动的控制方程为[16]

式中为压力水头，cm；x为方向笛卡尔坐标，cm；K为各向异性张量的无量纲分量；K为石英砂的饱和导水率，cm/min。

二维饱和介质中热运移控制方程为[17]

式中为石英砂的温度，℃；λ()为石英砂的表观热导率，W/(m·℃)；()和C分别表示多孔介质和水的体积比热容，J/(m·℃)。该方程忽略水汽弥散对热运移的影响；q为方向达西流速，cm/min；为时间，min。

多孔介质的体积比热容()具有广义可加性，可以表示为

式中为体积百分比，cm3/cm3；下标、分别表示多孔介质中固相和液相。由于本试验采用饱和状态下的石英砂，故认为有机质及气相两部分可忽略。

根据de Marsily（1986）[18]，表观热导率λ()可以表示为

其中，多孔介质导热系数0()为

式中为达西流通量密度，cm/min；δ为Delta函数；λ、λ分别表示纵、横向热弥散度，cm；1、2、3均为计算导热系数的经验参数。

1.3.2 初始条件与边界条件

模拟区域为50 cm×40 cm，采用有限元方法将区域划分为边长为1 cm的均匀三角形网格，共计4 000个。模拟区bc为供水边，ef为排水边，均定义为定水头边界，上下边界的水头差为6.5 cm。与水头边界相对应的温度边界设置为第1类温度边界，采用进、出水室内部实测的热电偶温度。其他边界设置为零通量边界。模拟区域初始含水率为各粒径石英砂的饱和含水率，初始温度为常温。

1.3.3 参数的设置及反演

不同粒径石英砂的体积比热容和残余含水率的取值参照文献[19]，详细取值如表2所示。待估参数分别为介质的饱和导水率（K）、导热系数0的经验参数（1、2、3）、纵向热弥散度（）和横向热弥散度（）。分别设置3种基于不同数据类型的反演情景对水热参数进行估计：仅采用观测点温度（R1）、观测点温度+水流通量（R2）和观测点温度+水流通量+热量损失（R3）。并对R1情景设置3种不同参数反演组合，即同时对2组参数（K和（1、2、3））、3组参数（K和λ、λ）和4组参数（K、（1、2、3）、λ和λ）进行估计。利用HYDRUS-2D中的反问题模型对参数进行估计，该模型采用Levenberg-Marquardt非线性优化算法，参数优化的目标函数为[12]

式中为、某方向坐标，cm；为实测值；v为待估参数类型；为待估参数。y为实测温度，y为相同测点、相同时刻（t）下的模拟温度，℃；m为每类待估参数的个数，n、w分别为实测温度的数量及其权重。本文采用石英砂内部温度对其待估的水热参数进行反演，初始值如表3所示。参数优化的目标函数采用的求解方法为最速下降法[20]。

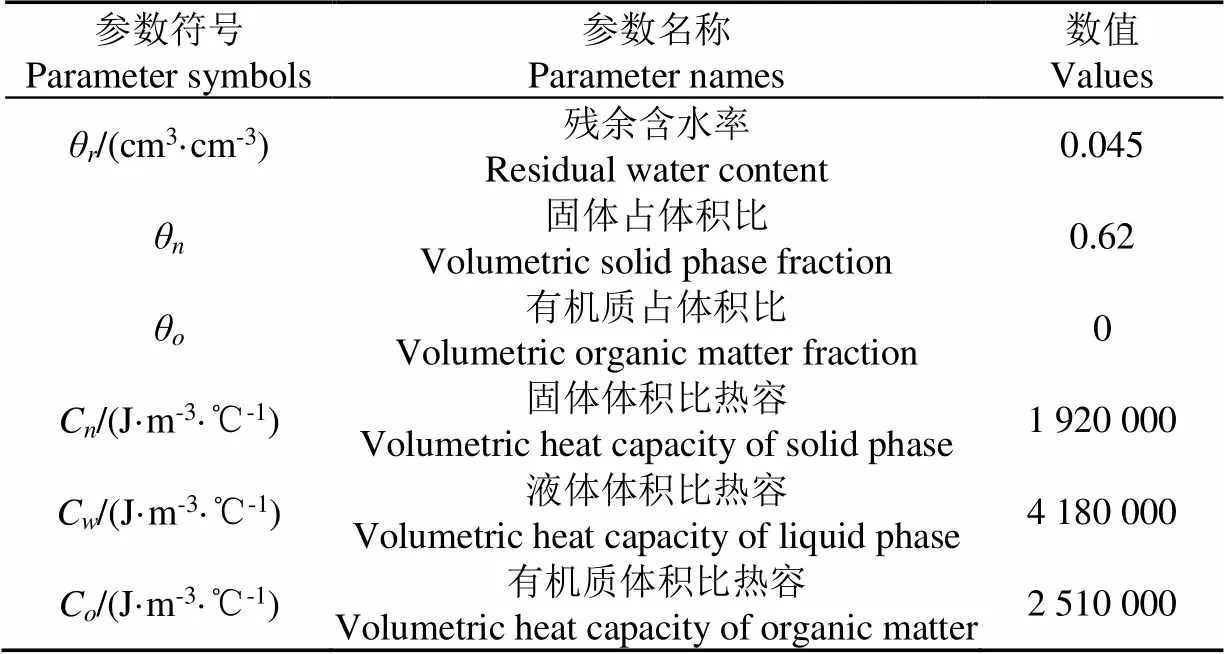
表2 模型中已知的水热参数设置

表3 待估参数的初值设置

进一步对介质的待估参数（饱和导水率、导热系数和纵向热弥散度）在模型中的参数敏感性进行分析。假设每个参数都是独立变化的，并加以±5%的参数扰动，并以式（7）中的作为评价指标[21]，对HYDRUS-2D模型中的3个参数进行敏感性分析。

=(O−O)/O（7）

式中O为参数扰动后的值；O为敏感性分析时参数的初值。

2 结果与分析

2.1 基于观测点温度的参数反演

在相同水力梯度和热源温度条件下，得到不同时刻的模拟温度空间分布随时间的变化如图2所示。结果表明，由于热源边界为部分线源边界，当热量随着水流运动进入砂箱后，砂箱中部升温较快，两侧温度变化较慢，并且在热运移锋前缘运动至出水边界之前，热运移锋都将保持这一温度分布趋势逐渐向前运动。当热运移锋前缘运动至出水边界后，砂箱中部与两侧的温差减小，整个砂箱温度也逐渐升高至接近进水室温度。试验期间由于热量损失始终存在且无法避免，距热源越近则热量损失越大。由于热量损失逐渐累积，因此当试验结束时砂箱温度仍然呈现出沿水流运动方向逐渐下降的变化趋势。3种不同粒径的均质石英砂具有相似的温度变化过程。由同一时刻不同介质中的温度分布可知，热运移锋的运动速率随石英砂粒径的增大而逐渐加快，表明输入相同水头条件下水流运动的平均速度是饱和均质粗砂最高，均质中砂次之，均质细砂最低。

图2 不同均质石英砂的模拟温度随时间（t）的变化

利用砂箱中20个热电偶的实测温度数据对饱和均质介质的水热参数进行反演。由于同时反演介质的水流和热运动参数具有较高的精度[12]，因此在仅采用观测点温度对介质水热参数进行反演（R1）的条件下设置3种反演情景：S1（对K和1、2、3进行估计）、S2（对K、和进行估计）和S3（对K、1、2、3、和同时估计），其中未参与估计的参数取初始值。饱和导水率、导热系数和热弥散度3个参数之间的相关性不强，Nakhaei 和Šimůnek[12]的研究结果表明，当采用HYDRUS的反问题模型对参数进行反演时，参与反演的参数个数小于6个时，能得到可靠的结果。不同反演情景下得到的均质中砂的水热参数如表4所示。

表4 基于温度数据的参数反演结果

注：S1表示介质热弥散度已知，估计介质饱和导水率和导热系数经验参数；S2表示导热系数经验参数已知，估计介质饱和导水率和热弥散度；S3表示同时估计饱和导水率、热弥散度与导热系数经验参数；#表示该参数未参与反演。

Note: S1 represents the thermal dispersivities are known and the empirical parameters of thermal conductivity and the saturated hydraulic conductivity are estimated; S2 represents the thermal conductivities are known and the thermal dispersivity and the saturated hydraulic conductivity are estimated; S3 represents the empirical parameters of thermal conductivity, thermal dispersivities and saturated hydraulic conductivity are estimated; # represents the parameter is not involved in estimation.

结果表明（表4），纵向弥散度的取值变化不大，基本稳定在1.00～3.44 cm之间，横向弥散度取值均为0.10 cm。将导热系数经参数1、2、3代入式（5）可计算得到饱和均质石英砂的导热系数（0）。S1情景下的中砂的0为1.10 W/(m·℃)，与表1中参考值（1.950 W/(m·℃)）差异较大，而S3情景下中砂0为1.93 W/(m·℃)，与参考值基本一致，表明同时对介质饱和导水率、导热系数和纵向、横向弥散度进行估计可以提高介质导热系数的估计精度。此外，在导热系数估计较为合理的条件下（即S2和S3情景），介质饱和导水率的估计精度较S1明显提高。3种反演情景下的温度时序曲线均具有较高的决定系数（2>0.85），表明模型模拟温度与实测温度拟合较好，且S3情景下的拟合温度精度最高，模拟累积流量的相对误差最小，因此选择S3反演情景对粗砂和细砂的水热参数进行反演，结果见表4。石英砂饱和导水率的估计值随介质粒径增大而增大，而介质纵向热弥散度则随粒径减小而增大，而横向热弥散度取值不变，均为0.10 cm。

以均质中砂S3情景下的参数值作为敏感性分析的参数初值，以整个石英砂层吸收的累积热量为目标，对以上3个水热参数进行敏感性分析，结果如图3所示。饱和导水率最为敏感，因此在模型模拟过程中要尤其关注饱和导水率的取值，以及其对温度空间分布的影响。导热系数和纵向弥散度的参数敏感性依次减小。

图3 待估参数敏感性分析

在利用观测点温度对介质参数反演的过程中，S3反演情景下参数具有比S1和S2更高的估计精度。尽管如此，模拟累积出流量与实测的累积流量间仍存在较大误差（如表4所示），说明仅利用温度数据对介质水热特性参数进行反演会造成较大的估计误差，尤其对参数敏感性高的参数——饱和导水率的估计影响显著。因此，需要结合试验过程中水流运动和热量传递的信息进一步分析以达到对介质水热参数准确估计的目的。

2.2 考虑水流通量和热量损失的参数反演

在仅利用观测温度对介质水热参数反演的基础上，分别增加实测水流通量和试验过程中的热量损失2种不同类型的数据对介质的水热参数进行反演，分别设置R2（观测点温度+水流通量）和R3（观测点温度+水流通量+热量损失）2个情景。其中热量损失通过计算观测点虚拟温度来实现，具体方法为：1）假设试验过程中所有损失热量（包括有机玻璃砂箱吸收的热量和散失到环境中的热量）均被石英砂层吸收；2）计算无热量损失条件下砂层应达到的温度，即虚拟温度。该虚拟温度可以认为是观测点实测温度与热量损失共同作用的结果，具体计算原理及方法可参考文献[22]。

不同介质中，基于水流通量和热量损失的参数反演结果如表5所示。结果表明，不同介质中，R2和R3情景下的饱和导水率估计值均大于S3情景。R2和R3情景下的介质纵向弥散度估值变化不大，横向弥散度的估计值则有所降低，表明垂直于水流方向的热量迁移有所减少，更多的热量交换发生在沿水流运动方向。纵横向的热弥散比变化范围在16.67～81.20之间，该结果与普遍认同的纵向弥散度与横向弥散度的倍数比例（10~100）基本一致[21,23]。

图4为基于不同类型数据的典型观测点（2-3）的实测与模拟温度随时间的变化图。砂箱内其余各观测点与典型观测点呈相似的温度变化过程。均质砂介质中，不同反演情景的模拟温度在试验前期具有较大差异，饱和导水率估值越高，前期温度升高越快；在试验开始20 min之后，不同反演情景的模拟温度间无明显差异。均质粗砂介质中，不同反演情景的模拟温度始终高于实测观测点温度，也具有饱和导水率估值越高，观测点温度升高越快的变化趋势。均质细砂中，由于饱和导水率估计值较小，且不同反演情景间差异不大，因此模拟温度时序曲线无明显差异。不同反演情景的模拟温度与实测温度均具有较高的拟合精度，2均大于0.93。

表5 基于不同类型数据的参数反演结果

注：R2表示用于参数反演的数据类型包括观测点温度和实测水流通量；R3表示用于参数反演的数据类型包括观测点温度、实测水流通量和热量损失。

Note: R2 represents measured temperature and water flux are used for estimation, R3 represents measured temperature, water flux and heat loss are used for estimation.

图4 基于不同类型数据的典型观测点模拟及实测温度穿透曲线

2.3 介质水热参数估计误差分析

对不同反演情景下的累积出流量的模拟结果进行分析，与实测值间的相对误差如图5所示。

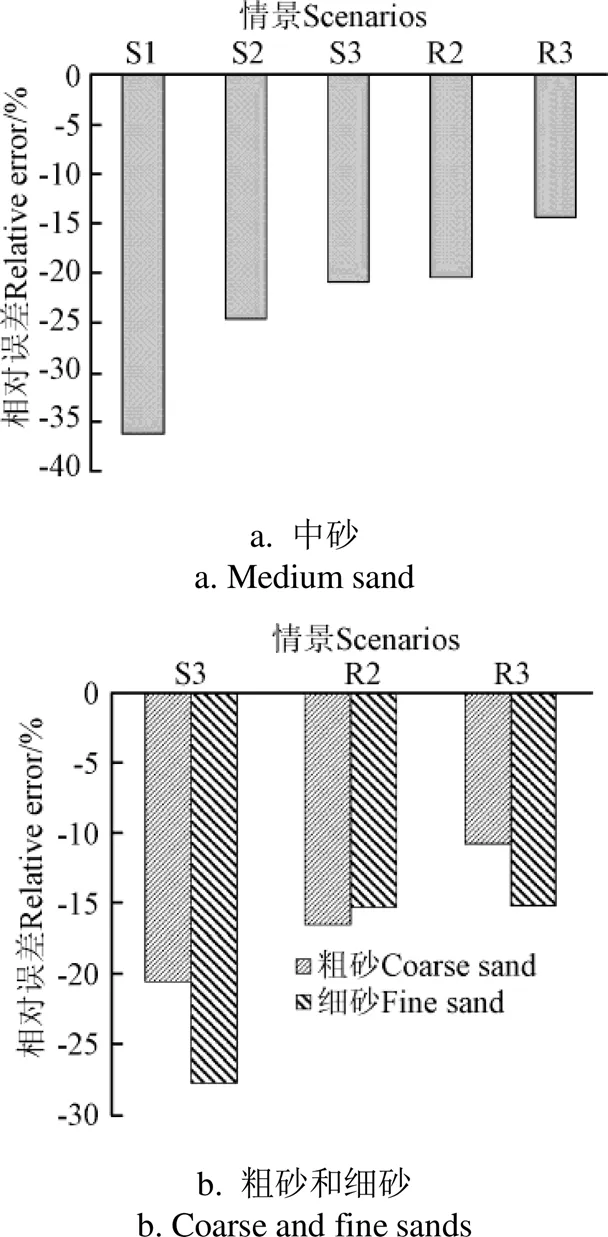
图5 不同反演情景下累积出流量的估计误差

如图5可知，在任何情景设置中累积出流量的估计值均低于实测累积出流量，且随着用于估计参数的数据类型不断增多，估计误差逐渐减小。与S3情景相比，R3情景下粗砂、中砂、细砂的累积流量相对误差分别减少了9.74、6.65和12.53个百分点，对细砂饱和导水率的估计精度提升最显著。尽管如此，在R3情景下3种均质介质的模拟累积流量仍存在10%～15%左右的估计误差。相关的试验和模拟研究中也存在水流通量估值偏低的问题：Hopmans等[24]认为热脉冲几何形状对热传导的影响以及模拟过程未考虑热弥散作用是导致估算水流通量偏小的主要原因；Ochsner等[25]提出估算误差产生是某种原因增大了对流项，但未解释产生这种现象的物理成因；而Gao等[26]则通过室内试验证明，在土柱试验中，壁面流会导致水流通量增大10%～20%，因此通过设置扩大系数（1.1～1.2）可以校正模型估算的水流通量。本试验采用的砂箱为有机玻璃材料，表面光滑，与石英砂颗粒接触不完全，易出现较大的孔隙，从而在砂箱内壁和石英砂层间形成水流的优先流动，导致实测累积出流量偏高。因此壁面流可能是本试验中造成模拟与实测水流通量存在差异的主要因素。

进一步对饱和均质介质的导热系数估计值进行分析（见图6）。

图6 不同反演情景下导热系数的估计误差

图6a表明随用于估计参数的数据类型不断增多，饱和中砂的导热系数估计精度逐渐提高（S2情景下导热系数未估计）；且除S1情景外，其余情景下的估计误差均低于5%，在合理估计的范围内。如图6b所示，粗砂和细砂的导热系数估计值始终与参考值存在较大差异，其中S3情景下的导热系数与参考值差异最小，R2情景下的导热系数与参考值差异最大。S3情景下的饱和粗砂导热系数估计值为3.76 W/(m·℃)，较参考值高估了54.28%；饱和细砂的导热系数估计值为1.43 W/(m·℃)，较参考值低估了22.78%。介质导热系数主要受介质自身结构、固体颗粒的导热系数、饱和度、压实程度等多种因素影响[27]。本试验中，细砂的粒径均匀统一，压实程度较高，而粗砂则由于存在较大颗粒，因此压实程度较低。不同的压实程度可能造成饱和多孔介质导热系数的估计误差。虽然粗砂与细砂的导热系数估计值与参考值存在较大差异，但饱和石英砂导热系数随孔隙度（饱和含水率）的变化趋势与参考值保持一致，即随着介质孔隙度增大，饱和石英砂的导热系数逐渐降低。

3 结 论

本文在开展3种不同粒径的饱和均质石英砂的热示踪试验的基础上，分别将不同类型的数据与HYDRUS模型相结合，对二维饱和均质介质的水、热运移参数进行了反演与分析。得到主要结论如下：

1）温度数据能反映均质介质中水热迁移过程，将其与HYDRUS-2D模型相结合可用来反演介质的水力与热力学参数。同时对介质饱和导水率、导热系数以及热弥散度进行估计，有利于提高水热参数估计精度；并且在导热系数估计较为合理的条件下可以减小温度数据对介质饱和导水率的估计误差。在恒定热源条件下，当砂箱吸收的热量不再变化，温度数据也不再体现不同介质间的渗透性差异。

2）饱和导水率是反演参数中敏感性最高的参数，增加用于参数反演的水流运动和热量传递信息时，粗砂、中砂、细砂的累积流量相对误差分别减少了9.74、6.65和12.53个百分点，显著提高了介质饱和导水率的反演精度。反演所得的饱和导水率估值随粒径的增大而显著增大。在观测点温度拟合较好的情况下仍存在10%～15%左右的水流通量估计误差，在考虑热量损失的条件下，壁面流可能是造成累积流量误差的主要原因。

3）导热系数和热弥散度在水热迁移模型中的敏感性均很低，纵向热弥散度随粒径的减小而增大，横向热弥散度则基本无变化。增加用于参数反演的水流运动和热量传递信息能显著提高中砂的导热系数反演精度。

[1]吴志伟，宋汉周. 地下水温度示踪理论与方法研究进展[J]. 水科学进展，2011，22(5)：733-739.

Wu Zhiwei, Song Hanzhou. Temperature as a groundwater tracer: Advances in theory and methodology[J]. Advances in Water Science, 2011, 22(5): 733-739. (in Chinese with English abstract)

[2]秦耀军，周晓勇，杨亚宾，等. 基于数据同化技术的地质参数反演分析研究[J]. 水科学与工程技术，2017(6)：78-82.

Qin Yaojun, Zhou Xiaoyong, Yang Yabin, et al. Back analysis of geological parameters based on data assimilation[J]. Water Sciences and Engineering Technology, 2017(6): 78-82. (in Chinese with English abstract)

[3]闵涛，周孝德，冯民权. 非线性布西尼斯克方程的直线解法及渗透系数反演计算[J]. 水利学报，2004，35(7)：21-25.

Min Tao, Zhou Xiaode, Feng Minquan. Numerical solution of Boussinesq equation based on straight-line method and inverse calculation of permeability coefficient[J]. Journal of Hydraulic Engineering, 2004, 35(7): 21-25. (in Chinese with English abstract)

[4]李守巨，上官子昌，刘迎曦，等. 地下水渗流模型参数识别的模拟退火算法[J]. 岩石力学与工程学报，2005，24(A01)：5031-5036.

Li Shouju, Shangguan Zichang, Liu Yingxi, et al. Parameter identification procedure for groundwater flow model with simulated annealing[J]. Chinese Journal of Rock Mechanics and Engineering, 2005, 24(A01): 5031-5036. (in Chinese with English abstract)

[5]刘晓楠，张朴，孔力，等. 基于SVD和DE反演方法的渗透率估计[J]. 华中科技大学学报：自然科学版，2014，42(9)：5-9，18.

Liu Xiaonan, Zhang Pu, Kong Li, et al. Permeability estimation based on singular value decomposition and differential evolution inversion method[J]. Journal of Huazhong University of Science and Technology: Natural Science Edition, 2014, 42(9): 5-9,18. (in Chinese with English abstract)

[6]王兵贤，王泽文，徐定华，等. 二维流Boussinesq方程渗透系数反演的变分伴随方法[J]. 水利水电科技进展，2010，30(6)：11-14.

Wang Binxian, Wang Zewen, Xu Dinghua, et al. Variational adjoint method for inversion of permeability coefficient of two-dimensional flow Boussinesq equation[J]. Advances in Science and Technology of Water Resources, 2010, 30(6): 11-14. (in Chinese with English abstract)

[7]任图生，邵明安，巨兆强. 利用热脉冲时域反射技术测定土壤水热动态和物理参数Ⅱ. 应用[J]. 土壤学报，2004，41(4)：523-529.

Ren Tusheng, Shao Ming’an, Ju Zhaoqiang. Measurement of soil physical properties with thermo-time domain reflectometry Ⅱ. application[J]. Acta Pedologica Sinica, 2004, 41(4): 523-529. (in Chinese with English abstract)

[8]任图生，邵明安，巨兆强，等. 利用热脉冲-时域反射技术测定土壤水热动态和物理参数Ⅰ. 原理[J]. 土壤学报，2004，41(2)：225-229.

Ren Tusheng, Shao Ming’an, Ju Zhaoqiang, et al. Measurement of soil physical properties with thermo-time domain reflectometry Ⅰ.theory[J]. Acta Pedologica Sinica, 2004, 41(2): 225-229. (in Chinese with English abstract)

[9]Anderson M P. Heat as a ground water tracer[J]. Ground Water, 2005, 43(6): 951-968.

[10]Constantz J. Heat as a tracer to determine streambed water exchanges[J]. Water Resource Research, 2008, 44: W00D10.

[11]Steenpass C, Vanderborght J, Herbst M, et al. Estimating soil hydraulic properties from infrared measurement of soil surface temperature and TDR data[J]. Vadose Zone Journal, 2010, 9: 910-924.

[12]Nakhaei M, Šimůnek J. Parameter estimation of soil hydraulic and thermal property functions for unsaturated porous media using the HYDRUS-2D code[J]. Journal of Hydrology, 2014, 62(1): 7-15.

[13]Giambastiani B M S N C, Mastrocicco M. Limitation of using heat as a groundwater tracer to define aquifer properties: experiment in a large tank model[J]. Environmental Earth Science, 2013, 70: 719-728.

[14]Saley A D, Jardani A, Ahmed A S, et al. Hamiltonian Monte Carlo algorithm for the characterization of hydraulic conductivity from the heat tracing data[J]. Advance in Water Resource, 2016, 97: 120-129.

[15]Somogyvari M, Bayer P. Field validation of thermal tracer tomography for reconstruction of aquifer heterogeneity[J]. Water Resources Research 2017, 53(6): 5070-5084.

[16]Bear J. Dynamics of Fluids in Porous Media[M]. New York: Academic Press, 1972.

[17]Sophocleous M. Analysis of water and heat flow in unsaturated-saturated porous media[J]. Water Resources Research, 1979, 15(5): 1195-1206.

[18]de Marisly G. Quantitative Hydrogeology[M]. London: Academic Press, 1986.

[19]潘梦绮，黄权中，冯榕，等. 基于热示踪的饱和层状介质水热参数反演[J]. 水利学报，2017，48(11)：1363-1372.

Pan Mengqi, Huang Quanzhong, Feng Rong, et al. Estimation of hydraulic and thermal parameters in saturated layered porous media based on heat tracing method[J]. Journal of Hydraulic Engineering, 2017, 48(11): 1363-1372. (in Chinese with English abstract)

[20]Donald W M. An algorithm for least-squares estimation of nonlinear parameters[J]. Journal of Society for Industrial and Applied Mathematics, 1963, 11(2): 431-441.

[21]Rau G C, Anderson M S, McCallum A M, et al. Heat as a tracer to quantify water flow in near-surface sediments[J]. Earth Science Reviews, 2014, 129: 40-58.

[22]Pan M Q, Huang Q Z, Feng R, et al. Improving the estimation of hydraulic and thermal properties of heterogeneous media via the addition of heat loss[J]. Vadose Zone Journal, 2019, 18(1): 180149.

[23]Constanz J, Cox M H, Su G W. Comparison of heat and bromide as ground water tracers near stream[J]. Ground Water, 2003, 41(5): 647-656.

[24]Hopmans J W, Simunek J, Bristow K L. Indirect estimation of soil thermal properties and water flux using heat pulse probe measurements: Geometry and dispersion effects[J]. Water Resources Research, 2002, 38(1): 1006-1019.

[25]Ochsner T E，Horton R，Kluitenberg G J, et al. Evaluation of the heat pulse ratio method for measuring soil water flux[J]. Soil Science Society of America Journal, 2005, 69(3): 757-765.

[26]Gao J Y, Ren T S, Gong Y S. Correcting wall flow effect improves the heat-pulse technique for determining water flux in saturated soils[J]. Soil Science Society of America Journal, 2006, 70(3): 711-717.

[27]Ochsner T E, Horton R, Ren T S. A new perspective on soil thermal properties[J]. Soil Science Society of America Journal, 2001, 65(6): 1641-1647.

Estimation of water and heat transfer parameters of saturated silica sand by using different types of data

Pan Mengqi, Huang Quanzhong※, Feng Rong, Huang Guanhua

(1.,,100083,; 2.,,100083,)

The hydraulic and thermal parameters of soil and aquifer are very important for quantitative description of soil water, groundwater migration and its accompanying heat and salt transport. In order to investigate the influence of different types of data on the hydraulic and thermal parameter estimation, three heat tracing experiments packed with saturated homogeneous silicon sand of three different particle size (coarse, medium and fine sands) were conducted under steady state. Twenty T-thermocouple probes were installed uniformly in the sandbox to record the temperature of the silicon sand. Two additional T-thermocouple probes were installed in the inflow and outflow chambers to record the water temperature. And then, the measured temperatures of silicon sand and water were applied for the inverses model of HYDRUS-2D software to estimate the saturated hydraulic conductivity, the thermal conductivity and the longitudinal and transverse thermal dispersivity of three saturated silicon sands. In this study, three scenarios based on different types of data were designed to estimate these parameters, i.e. R1 (including the measured temperature at the observation point alone), R2 (including the measured temperature at the observation point and the cumulated outflow) and R3 (including the measured temperature at the observation point, the cumulated outflow and the heat loss). In the addition, three more scenarios under scenario R1 consisted of different numbers of parameters were set, i.e. S1 (the thermal dispersivities were known and the empirical parameters of thermal conductivity and the saturated hydraulic conductivity were estimated); S2 (the thermal conductivities were known and the thermal dispersivity and the saturated hydraulic conductivity were estimated); S3 (the empirical parameters of thermal conductivity, thermal dispersivities and saturated hydraulic conductivity were estimated). The results showed that the thermal conductivity, the longitudinal and transverse thermal dispersivities and the saturated hydraulic conductivity of silicon sand estimated at the same time could significantly improve the accuracy of parameter estimation, and the accuracy of the saturated hydraulic conductivity was improved when the thermal conductivity was reasonable under scenario R1. The saturated hydraulic conductivity was the parameter with the highest sensitivity in parameter estimation, followed by the thermal conductivity and the longitudinal thermal dispersivity. When the simulated temperatures were consistent with the measured temperatures at observation points, there was still 10%-15% estimated error of cumulated outflow. When considering heat loss, wall flow may be the main reason for the estimated error of cumulated outflow. The additional information of water flow and heat loss was helpful to reduce the estimated error of saturated hydraulic conductivity, and then the relative error of cumulated outflow was significantly decreased for coarse, medium and fine sands. The estimated value of saturated hydraulic conductivity increased with the increasing of particle size of silicon sands while the longitudinal thermal dispersivity showed the opposite trend. And the value of transverse thermal dispersivity was same for all the sands. The additional information of water flow and heat loss improved the estimation of thermal conductivity of medium sand as well. The estimated value of thermal conductivitydecreased with increasing particle size of silicon sands. This study can help for parameter estimation of homogeneous porous media based on different type of data.

data; parameters; heat tracing; saturated silica sand; water flow and heat transport models; HYDRUS-2D software

潘梦绮，黄权中，冯榕，等. 采用不同监测数据组合反演饱和均质石英砂水热运移参数[J]. 农业工程学报，2020，36(10)：75-82.doi：10.11975/j.issn.1002-6819.2020.10.009 http://www.tcsae.org

Pan Mengqi, Huang Quanzhong, Feng Rong, et al. Estimation of water and heat transfer parameters of saturated silica sand by using different types of data[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2020, 36(10): 75-82. (in Chinese with English abstract) doi：10.11975/j.issn.1002-6819.2020.10.009 http://www.tcsae.org

2020-01-10

2020-05-10

国家自然科学基金项目（51779256、51639009）；国家重点研发计划项目（2016YFC0501304）

潘梦绮，博士生，主要从事多孔介质中水热迁移规律的研究。Email：panmengqi@cau.edu.cn

黄权中，博士，教授，主要从事多孔介质水-热-盐运移机制及定量表征的研究。Email：huangqzh@cau.edu.cn

10.11975/j.issn.1002-6819.2020.10.009

P641

A

1002-6819(2020)-10-0075-08