一种面向大规模二维点集数据的密度聚类算法

王小林，付 山，邰伟鹏，胡 涛

(安徽工业大学a.计算机科学与技术学院；b.工程研究院，安徽马鞍山243032)

聚类是无监督机器学习中的代表，通过聚类可从大量数据中挖掘出有价值的信息[1]。目前聚类算法被广泛用于生物医学、图像处理等领域中[2-3]，其大致可分为：划分的聚类算法[4]，如K-means 等；密度的聚类算法[5]，如DBSCAN(density-based spatial clustering of applications with noise)等；网格的聚类算法[6-7]，如GG(grid-growing clustering algorithm for geo-spatial data)和CBSCAN(cell-based DBSCAN for location big data)等；模型的聚类算法[8]，如EM(expection-maximization algorithm)算法等。密度聚类可识别任意形状的簇且对噪声点不敏感，故其在数据挖掘甚至多维数据聚类中受到关注[9],以Ester 等[5]提出的DBSCAN 算法最为典型。DBSCAN算法中数据点位置对机器来说是透明的，需重复且广泛地遍历节点，对于大型数据集聚类效率较低，且数据量越大聚类时间越长。Wang等[10]提出了一种并行的DBSCAN算法，有效解决了理论与实践之间的鸿沟，但并行代价较高，不具有普适性；Kumar等[11]提出了一种基于图Group索引的DBSCAN算法，适当提高了DBSCAN 算法的聚类效率，但对大规模数据集没有进行详细研究；Boonchoo 等[12]通过改进DBSCAN 算法的聚类方式，提出以低密度优先来缓解高密度数据，但缺乏大规模数据集的研究；He 等[13]、Kim等[14]、Hu等[15]使用外部工具Mapreduce平台实现密度聚类算法，虽提升了聚类的效率和准确率，但需专用处理器等外部设备支持，不属于一种低代价高效率的算法。

使用DBSCAN算法对二维点集聚类时，由于参与聚类的点集数量庞大，且DBSCAN算法是通过遍历所有点并利用欧式距离判断点是否属于邻域内，会多次遍历到相同的点，导致重复计算，耗费大量时间。针对DBSCAN算法效率低下且无法处理大规模点集数据的问题，提出一种基于划分网格的密度聚类算法，且在OSM(open street map)路网节点数据预处理后的二维坐标点集下，采用提出的GDSCAN 算法和DBSCAN 算法进行不同规模数据的测试，验证GDSCAN算法的聚类效率。

1 DBSCAN密度聚类算法

DBSCAN算法是一种基于密度的空间聚类算法，涉及两个预设参数:邻域半径reps，事先给定数据点的邻域范围半径，用以限定待统计点的范围；密度阈值Tminpts，在数据点reps邻域范围内的点密度。

传统DBSCAN算法使用圆形作为密度邻域，并通过欧式距离判断数据点是否在当前数据点邻域内，如式(1)所示以二维空间为例，通过欧式距离计算点(xi,yi)与数据点(a,b)的半径邻域关系。

若满足式(1)，则表示点(xi,yi)参与点(a,b)的密度值计算，否则不予考虑。

设原始数据集为D，对于任意数据点p，记以点p 为圆心、reps为半径邻域内的邻居点集为Np，用|Np|表示点集包含的点数量。对于数据集D 中的每个点，传统DBSCAN算法将其分为3类。

1)核心点对任意数据点p，若p 的reps邻域内邻居点数量 ||Np≥Tminpts，则称点p 为核心点。

2) 边界点 对任意数据点p，若p 的reps邻域内邻居点数量 ||Np＜Tminpts，但存在一个邻居点q(q∈Np)，且|≥Tminpts，即q是核心点，则称p 为边界点。

3)噪声点 若任意点p 的reps邻域 ||Np＜Tminpts，且不存在任意点r ∈Np为核心点，则点p 为噪声点。即若p 既不是核心点也不是边界点，则其为噪声点。点类型的决策过程如图1。

给定数据集D，对于D中的任意两个位置点，他们之间存在3种密度关系:直接密度可达、密度可达和密度相连。若点p 在q 的reps邻域内，且q 为核心对象点，则称p 是q 发出的直接密度可达；对于位置点集合{ }p1,p2,p3,…,pb⊆D，若pi+1(i=1,2,3,…,n-1)是pi发出的直接密度可达，则称p1直接密度可达pn；若存在对象点o ∈D，且p 到o为密度可达，且q 到o为密度可达，则称p 到q 为密度相连。

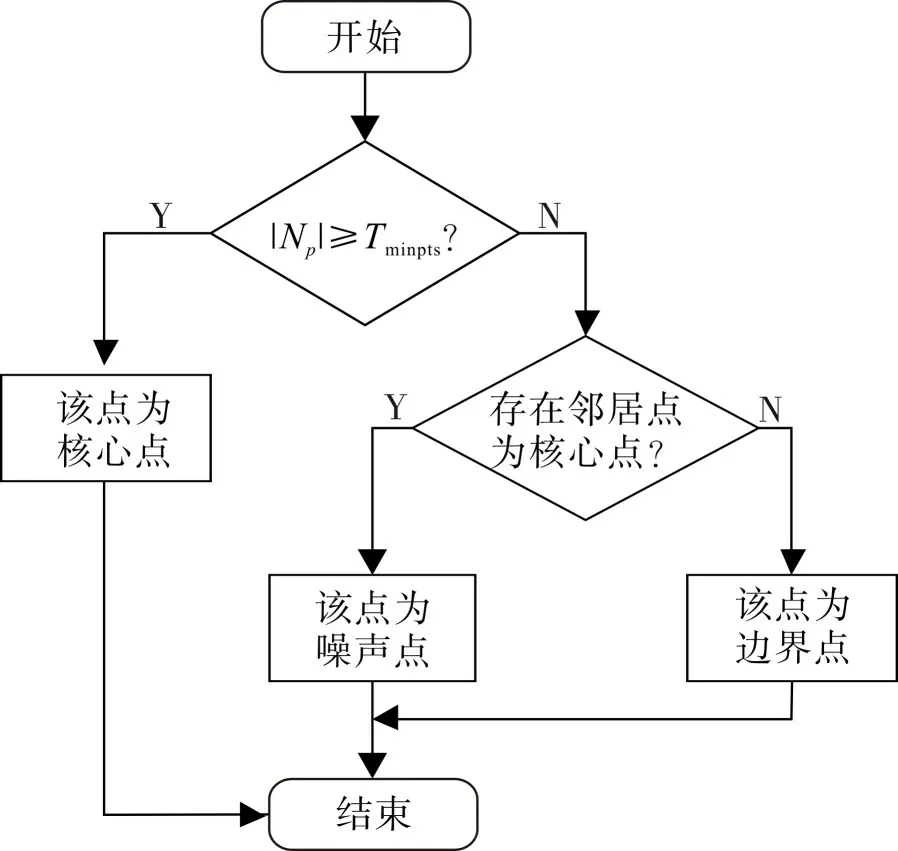
图1 点类型决策流程Fig.1 Decision process for point type

DBSCAN 聚类算法过程为:首先，随机选取一点记为p，通过遍历点的reps邻域来搜索簇，如果点p 的reps邻域包含多于Tminpts个点，则创建一个以p为核心点的簇；然后，通过迭代的方法从核心对象点到直接密度可达对象逐步扩张、聚集，当无核心对象点添加到簇中，整个迭代过程结束，同时得到若干划分的簇。点只提供坐标信息，在确定邻域内包含的点个数是否大于Tminpts时，需计算出邻域中心点和其他点的位置关系，通常使用欧氏距离来判断任一点是否被包含在reps邻域内。点数量较少时，其判断位置需要的计算量也较少；面对大量点数据时，计算点之间的距离会造成大量的等待时延，且这个时延随着数据点的增多呈指数增长，造成时间和内存的浪费。

2 基于划分网格的DBSCAN算法

图2 Grid dividing-based DBSCAN算法流程图Fig.2 Algorithm flowchart of grid dividing-based DBSCAN

针对传统DBSCAN 算法不能较好适应大规模数据的聚类情况，提出基于划分网格的密度聚类算法GDSCAN。对于二维坐标点集，取其最小及最大的坐标(xmin,ymin)，(xmax,ymax)，并以此确定其最小外包矩形；综合最小外包矩形大小和原始数据的特性确定邻域半径reps，以reps作为网格边长将最小外包矩形划分成若干网格，网格边长≥reps。计算开始时随机选取一个未遍历的点作为起点，通过给定reps及Tminpts逐步迭代扩张，填充核心对象点集。在填充和聚类过程中，计算reps邻域点集个数时，点必定存在于某一网格中任意位置，其邻域范围不可能超出以该网格为中心的所有直接相连网格（直接可达网格）。因此，只需考虑中心网格和直接可达网格内的点进行距离计算，直接过滤大量较远的点，以实现对核心对象集合的填充或对点的聚类。算法流程框图如图2。

点的直接可达网格示意如图3。由图3可看出:当网格划分为正方形时，记9 个网格的范围为RRec。以点p 为例，p 所在的正方形网格5为中心网格，则1，2，3，4，6，7，8，9为其直接可达网格。网格边长为r(r ≥reps)，为使中间网格内任意点的邻域圆位于其直接可达网格内，网格边长最小r=reps。若点p 位于中心网格的非边框部分，则其reps邻域位于中间的圆内。记邻域内的点集为N，则N 的分布范围RN⊂RRec。若点p 位于中心网格的顶点处，分别以中心网格四角为圆心的圆，由于圆的半径等于网格边长，所以4 个圆的范围不会超过9 个网格。若取网格边长大于reps，则圆处于被包含的状态，同样无法超过9个网格的范围。同理，若点p 位于中心网格除顶点的边上，以p 为圆心，reps为半径的圆Op，当且仅当r=reps时，Op与最外层的网格相切，当r ＞reps时，Op永远被包含在9个网格内。这样，对于点p，其reps邻域内的点只存在于9个网格内，且不包含4个角不与圆相交的区域。对于游离在9个网格外的点，由于其不被包含在点p 的reps邻域内，其完全不用参与距离的计算。记 ||Np点p 的reps邻域内包含的点个数，若 ||Np≥Tminpts，在下一步判断核心对象点时再次构建其直接可达网格计算邻域内点数量。

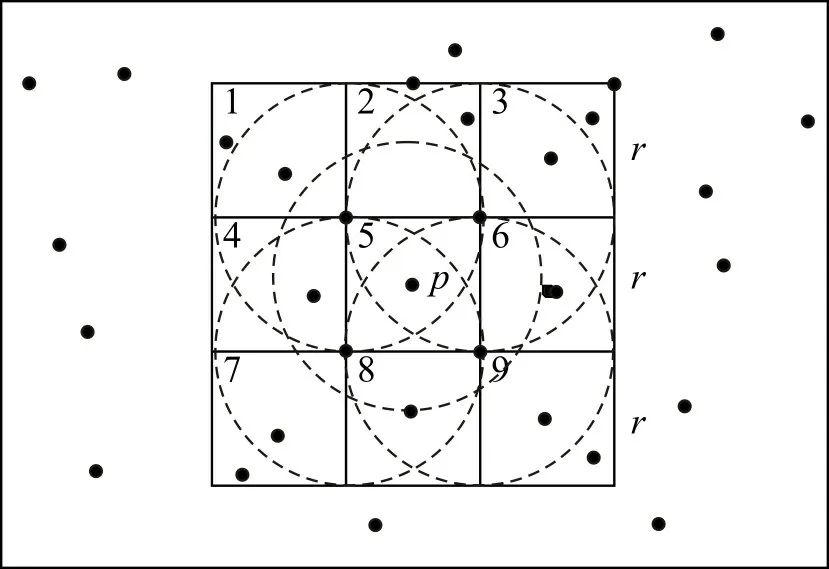
图3 点的直接可达网格示意图Fig.3 Schematic diagram for direct reachable grid of points

受原始数据离散情况等外部因素影响，往往点分布的图不可能正好划分为若干正方形，但同样可等分为若干相同大小的长方形。将原始点分布图划分成若干等大小的长方形，取长方形最短边l 为划分标准，满足长方形最短边l ≥邻域半径r，其邻域范围示意图如图4。由图4 可看出:当且仅当l=r时，点在中心网格上下边(包括端点)时，其生成的邻域圆与网格形成相切的关系；当l ＞r 时，同正方形网格一样，中心网格中任意一点，其邻域包含在中心网格的直接可达网格范围内，这种情况同样适用。

若取长方形最长边为划分标准，其邻域范围示意图如图5。由图5可看出，以中心网格顶点为圆心作邻域圆，点的邻域范围超出中心网格及其直接可达网格范围，需扩大网格范围以及数量。因此，不考虑使用长方形网格最长边为划分标准。

对点p 的邻域密度值判断后，对下一点重新选取中心网格和直接可达网格，从而只计算网格内的点，这样在迭代过程中可大大减少点距离的判断，直接减少计算量，极大提高算法效率。算法步骤流程图如图6。

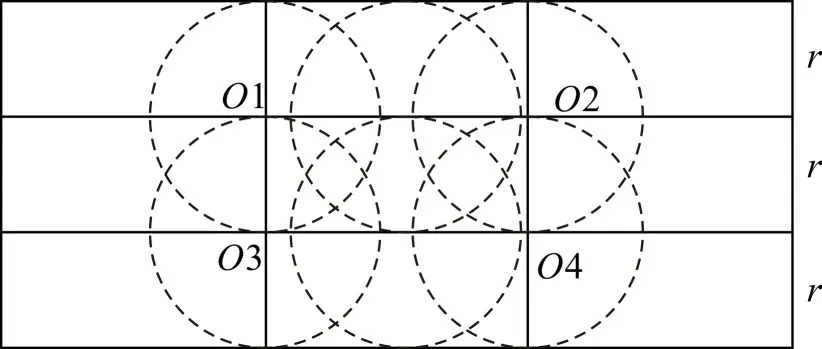
图4 以长方形网格最短边为标准的邻域范围示意图Fig.4 Schematic diagram of neighborhood range with the shortest edge of rectangular grid as standard

图5 以长方形网格最长边为标准的邻域范围示意图Fig.5 Schematic diagram of neighborhood range with the longest edge of rectangular grid as standard

图6 GDSCAN算法流程图Fig.6 Algorithm flowchart of GDSCAN

3 实验结果及分析

3.1 实验环境及条件

实验测试设备为1台PC 机，Windows10系统，配置为i5-8400 六核CPU，主频为2.80 GHz，16 GB 内存，1 T机械硬盘。使用Visual Studio 2012开发软件以及C++语言实现DBSCAN和GDSCAN算法。

实验数据取自OSM 官网，为美国东北部区域的路网数据，大小约16 GB，是一个XML格式文件。使用Python中Numba库中特定的XML结构解析包xml.etree.cEl-ementTree分析原始文件，同时使用jit装饰部分函数加速程序运行，最终得到两个目标文件，node.txt，way.txt。node文件中保存了路网中节点和节点的邻接点信息，按行保存，每行结构为{'Nd':node_id,'X':x,'Y':y,'Nn':Nn}。其中:Nd为节点在路网中的唯一标识；x，y为节点在路网中的横轴和纵轴坐标；Nn为node_id的邻接点集合。way文件中的数据按行保存，每行数据结构为{'Wd':way_id,'Wn':Wn}，其中:Wd为路在路网中的唯一标识；Wn为路在路网中包含的节点集合，节点只保存id。这两个文件主要保存邻接点信息，故可以通过文件进一步处理出叉路口点，叉路口点的定义如下。

定义1(一叉路口点)路网中存在一条路L(a，b)∈S，a，b分别为该条路的端点，a，b∈N，且a，b∈L，则称a，b称为一叉路口点。

定义2(二叉路口点)路网中存在一条路L(L∈S，S为路网中所有路的集合)，若存在一点c∈L且c只在L一条路上，则称c为二叉路口点。

定义3(三叉路口点)若路网中存在一点c∈N，当且仅当有3条路L1，L2，L3∈S，L1∩L2∩L3=c，且c为3条路的端点，则称点c为三叉路口点。

以此类推可得到m叉路口点的定义，最终得到的二维坐标形式的叉路口点即为经过处理的聚类原始数据集。其中只有坐标(x，y)在聚类算法中起作用，其余附加信息用于构建索引、查询信息等环节。

3.2 聚类结果分析

对原始数据集预处理后，使用密度分布特征明显的四叉路口点进行聚类，同时使用外包多边形包裹区分不同簇。算法参数需人为确定，在OSM路网数据中，点之间的距离以点坐标单位为衡量标准时彼此相距较远，选取Tminpts=10，reps=100 时，符合本实验数据密度分布。网格依据点的最小外包矩形图平均划分，单个网格长为578、宽为519。原始四叉路口散点图如图7，GDSCAN 算法聚类结果如图8，对图8进行局部放大，结果如图9。

图7 四叉路口散点图Fig.7 Scatter plot of four-forked intersection

图8 四叉路口聚类结果Fig.8 Clustering results of four-forked intersection

图9 聚类结果局部放大图Fig.9 Partially enlarged view of clustering results

比较图7～9 可看出，点的密度分布呈东密西疏的特点，符合实际情况，即美国东北部的西南地区较为繁华，其余区域欠佳，因此西南方的叉路口数相对多。由此表明，聚类较好地保留了四叉路口的密度特性，可清晰区分出不同的簇，GDSCAN 算法的聚类效果较为理想。

为了进一步测试GDSCAN算法的运行效率，从实验数据点集中抽取部分点进行GDSCAN 和DBSCAN 算法的速率测试实验。在保证实验参数与上文相同的情况下，对不同数量级的数据均进行10 次测试，并取平均耗时，对小于10 000 个点的的结果使用折线图展示，结果如图10。

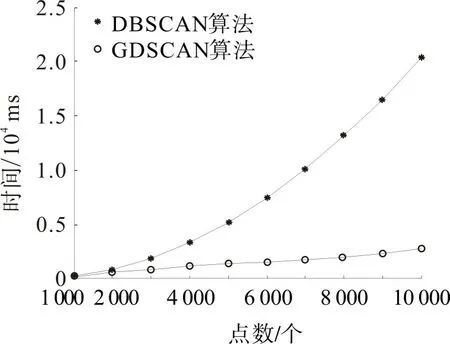
图10 两种算法在不同数据集下的聚类耗时Fig.10 Clustering time of two algorithms underdifferent data sets

从图10 可看出:数据点在2 000 个以下时，GDSCAN 和DBSCAN 算法的聚类耗时无显著差距，GDSCAN耗时稍短；随数据点增加，DBSCAN耗时极速增长，数据点达到10 000 个时，DBSCAN 需20 s才能将点聚类成功；而GDSCAN随着数据集中点的增加，耗时平稳线性增长，当数据集内点达到10 000 个时，聚类耗时仍低于5 s，此时DBSCAN 耗时为GDSCAN的4倍多。

表1为数据点达到200 000个时，两种算法的聚类耗时。由表1可看出，数据点达到200 000个时，DBSCAN 的聚类耗时是GDSCAN 的44 242 倍；数据点达到400 000 个时，DBSCAN 的聚类耗时是GDSCAN的94 293倍；对于500 000～700 000个数据点的大规模数据集，GDSCAN算法聚类耗时仍保持平稳增长(DBSCAN耗时巨大，故仅记录GDSCAN算法的聚类耗时)。

上述结果表明:DBSCAN算法聚类耗时依赖原始数据集的大小，数据集较小时处理时间在承受范围内，数据集增加时处理时间过长；而基于网格的DBSCAN算法在聚类过程中对原始数据集大小的依赖性低，在不同等级的数据集中都具较好表现；就本次北美路网数据的聚类处理而言，使用网格密度聚类算法具有较高的时间效率和较好的聚类结果。

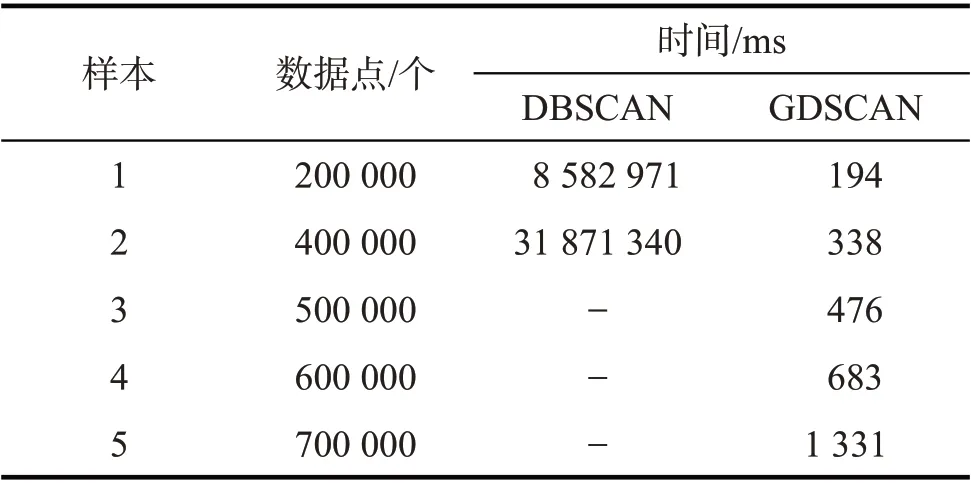
表1 两种算法的聚类耗时Tab.1 Clustering time of two algorithms

4 结 论

针对DBSCAN 算法对大规模数据聚类效率低下的问题，使用划分网格的方法对DBSCAN 算法进行改进，提出一种基于划分网格的密度聚类算法GDSCAN。以美国东北部区域的路网为实验数据，采用GDSCAN算法对其进行聚类，并与DBSCAN算法的聚类耗时进行比较。结果表明，GDSCAN算法对大规模数据的处理较为理想，聚类效率有较大提升。但在合适的网格边长和半径的选取上GDSCAN算法还有进一步优化的空间，后续研究将从邻域半径、网格边长与数据点的关系考虑更高效合适的参数。