一堂“失控”的公开课
韦传慧
摘 要:二次函数是重要的数学模型,是初中数学学習的重点与难点,同时二次函数的图像、性质及用二次函数解决实际问题也是中考的高频考点。为此,我们初三数学组就这个专题开设了关于二次函数的两节复习课,我也积极参与,并以“二次函数的图像与性质”作为重点开了一节公开课。
关键词:二次函数;失控;公开课
二次函数是重要的数学模型,是初中数学学习的重点与难点,同时二次函数的图像、性质及用二次函数解决实际问题也是中考的高频考点。为此,我们初三数学组就这个专题开设了关于二次函数的两节复习课,我也积极参与,并以“二次函数的图像与性质”作为重点开了一节公开课。
“工欲善其事必先利其器”,在课前我进行了精心的备课,以夯实学生基础为主,重视课本,注意前后知识的联系,建立知识网络串联知识点,设计课堂的每一个环节,并力争做到能力与知识并重。
上课伊始,我从梳理知识点出发,用问答的形式,带着学生复习了二次函数的定义、性质。接下来,我以习题带知识点的形式具体复习了抛物线的开口方向、对称轴、顶点坐标、增减性,以及利用配方法、顶点公式法把二次函数从一般式写成顶点式及二次函数表达式的几种基本求法。数形结合是非常重要的数学思想方法,始终贯穿二次函数的教学,所以接下来的环节我结合具体的表格、图像并一连串的问题来让学生进行识图、识表练习,由于是复习课,学生经过前一阶段的学习,已经具备了一定的知识积累与解题经验,所以这几个环节都很流畅,基本在我的掌控之下。
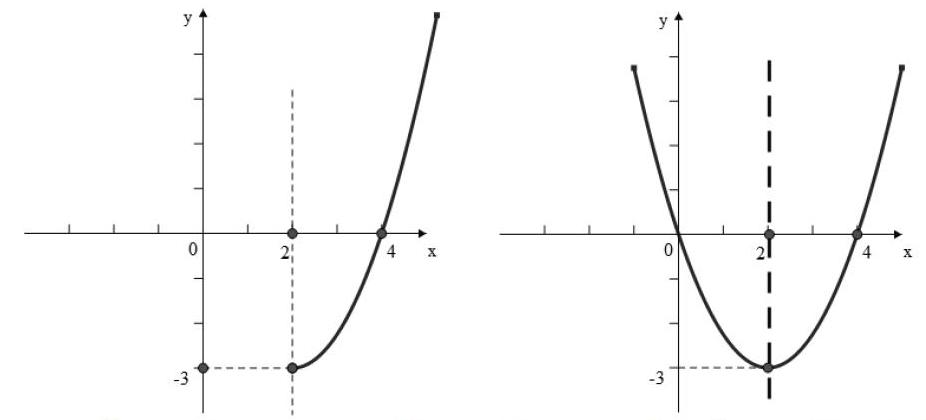
数学是严谨的,可它也是自由的,所以在日常的教学中,我的课堂经常会设置一些开放性的问题,因为相较于传统的数学问题,此类问题一般来说条件不完备、解法不唯一、答案不确定,要求学生从多角度、多层次去进行思考与探索,这极好地锻炼了学生思维的广度与深度,并从一定程度上培养了学生的创新能力。所以在课的倒数第二个环节我设置了一道开放性的题目(如下图),先要求学生把左图补充完整,可得右图,然后结合右图抛出
问题:“由这个二次函数的图像,你看到了什么?想到了什么?得到了什么?”在设计这道题的时候,我是考虑到我们班的实际情况的,所以对这道题的定位是低起点、宽入口、拓展性强,旨在让不同层次的学生都参与进来,因为平时我发现就算数学基础再差、再不爱学数学的学生往往也会积极主动的参与到此环节中来,因为在此类问题中总能找到他们能解决、会回答的问题,从而也总是让他们找回一些学习数学的自信来。果然在这个环节,课堂气氛空前热烈,几乎所有的学生都参与进来:由图像的形状确定a、b、c的符号;图像的顶点坐标;图像的对称轴;函数的最值;图像与x轴、Y轴的交点坐标;Y=0时,一元二次方程的根的情况等等,这些均可由图像直接或间接得到,都不是很难的问题,我也特意点了那些基础较差的学生回答,他们也表现的很好,时间一分分的过去了,这个环节,我设置的时间是5-7分钟左右,不知是课堂气氛太好,还是学生急于表现,他们又接二连三地提出了新的问题,新的发现,新的结论:这条抛物线的表达式能否求出?怎么求?可以用哪几种方法求?将函数图像沿着X轴或Y轴翻折后,顶点坐标有何变化?表达式如何求?将图像如何平移才能与X轴只有一个交点?函数图像如何平移顶点才能与坐标原点重合?等等,平时一些我上课用来拓展补充的知识点,也被他们一一运用到这道题中来,时间已超出我设置的时间1分钟、2分钟、3分钟……,我有心拿回课堂的控制权以便进行最后一个课堂检测反馈环节,可看着学生那一双双跃跃欲试的眼,急于表现的神情,我迟疑了,苏霍姆林斯基说过:“让学生体验到一种自己亲身参与掌握知识的情感,乃是唤起少年特有的对知识的兴趣的重要条件。”所以最终我放弃了,我的课堂“失控”了,这个环节整整多用了预计时间的一倍。
当然这堂课的最后,我的教学计划未能全部完成,对于一堂公开课来说,或许它不够完美,可对于我个人来说,这是一个多么难得的体验,因为就在那一刻,我顿悟:每一个学生都是一个独立的个体,哪怕是数学学得再不好的学生,他们都有自己独特的思维方式以及解决问题的策略,人的大脑是最神秘最不可思议的器官,人的潜力永远是无穷的,我们平时眼中所谓的笨孩子、懒孩子,或许只是他们失去了学习数学的兴趣、失去了思考问题的动力,我们难到不应该好好反思一下我们的课堂是从什么时候开始失去了对他们的吸引力,我们又应该怎样经营好我们的课堂,让那部分孩子重拾自信,提高兴趣,回归课堂。叶圣陶说过,培育能力的事必须不断地去做,又必须随时改善学习方法,提高学习效率,才会成功。我想对于我们教师来说,这话同样适用,在我们日常的教学中,可能随时会发生像今天这样的“不完美”,存在着这样或那样的缺憾,可我们要认真对待每一次的缺憾与不完美,在这些最平常、最真实的实践中获得宝贵的教学经验与灵感,反思与调整我们教学的思路与前进的方向,并日复一日地去坚持做这样的一件事,我想最终的结果一定是我们的老师更专业,我们的课堂更加有吸引力。
师者,人类灵魂的工程师,哪怕是教的看似枯燥无味的数学,你也要有直击学生灵魂的本事,要让他们真正体验到数学这门学科的魅力及其自由的本质,而不能一味地强加、灌输,或许这就是教书匠与灵魂工程师的区别。教师之为教,不在全盘授予,而在相机诱导,善思则得,善诱则通,诱思交融,百炼成钢!
参考文献
[1] 吴新建.关于初高中数学衔接的思考---以高中二次函数教学为例[J].中学数学月刊,2014(7):18-19.
[2] 朱锐.谈数学课堂的"数学味道"—公开课"二次函数的图象与性质4"两次授课的教学思考[J].亚太教育,2015(12):77-77.

